面向柔性加工的拐角运动策略研究与应用

张 静,仲济磊,陈珍萍,吴 祥

(1.无锡开放大学 机电与信息学院,江苏 无锡 214001;2.苏州科技大学 电子与信息工程学院,江苏 苏州 215009;3.浙江工业大学 信息工程学院,浙江 杭州 310023)

近年来,计算机辅助系统被广泛应用于数控机床自动加工领域,其中NURBS和B-splines等平滑曲线被普遍应用于复杂图案的插补拟合[1-4]。然而大多数数控机床无法实时有效地插补高阶参数曲线,主要原因在于样条函数计算量大,且受多参数因子影响。虽然目前NC系统用“点对点”运动指令实现对高阶参数曲线的线性插补,但是直线段组成的内插路径易导致数控系统运动不连续,即运动会在转角处停止,导致运动周期时间延长,并产生粗糙的转角表面[5]。为实现多个小线段之间的连续过渡,尖锐的拐角会被数控系统替换成平滑的混合曲线,此时参考路径偏离了原始的加工几何形状而形成轮廓误差。因此,众多专家学者针对连续转角的连续性、准确性和高速性进行了一系列研究。Tajima等[6]通过分段加速度的方式在轨迹的拐角处进行了运动学平滑,优化了给进轴的速度,缩短了加工时间。王勇等[7-8]针对文献[6]中没有对拐角轮廓进行深入研究的情况,提出中点约束算法解决轮廓重叠问题。冯倩倩等[9]提出了基于曲线的短线段拐角实时插补算法,虽然实现了直线段与曲线的平滑转接,但是规划过程存在计算量大的问题,影响系统的实时性能,难以应用到实际工程中。

因此,笔者提出了一种面向柔性加工的拐角运动策略。该策略首先通过设计轴的运动曲线来生成平滑和可控的转角轨迹,计算出拐弯处的最大约束速度,实现速度跟随方向动态的平滑过渡;其次,设计了软件双轴同步插补补偿模型,降低了机械本体的抖动,提高了加工精度和稳定性。该算法的突出优点是计算量小,速度快,精度高,便于在嵌入式设备上部署。

1 运动控制算法

1.1 运动学上的转角平滑问题

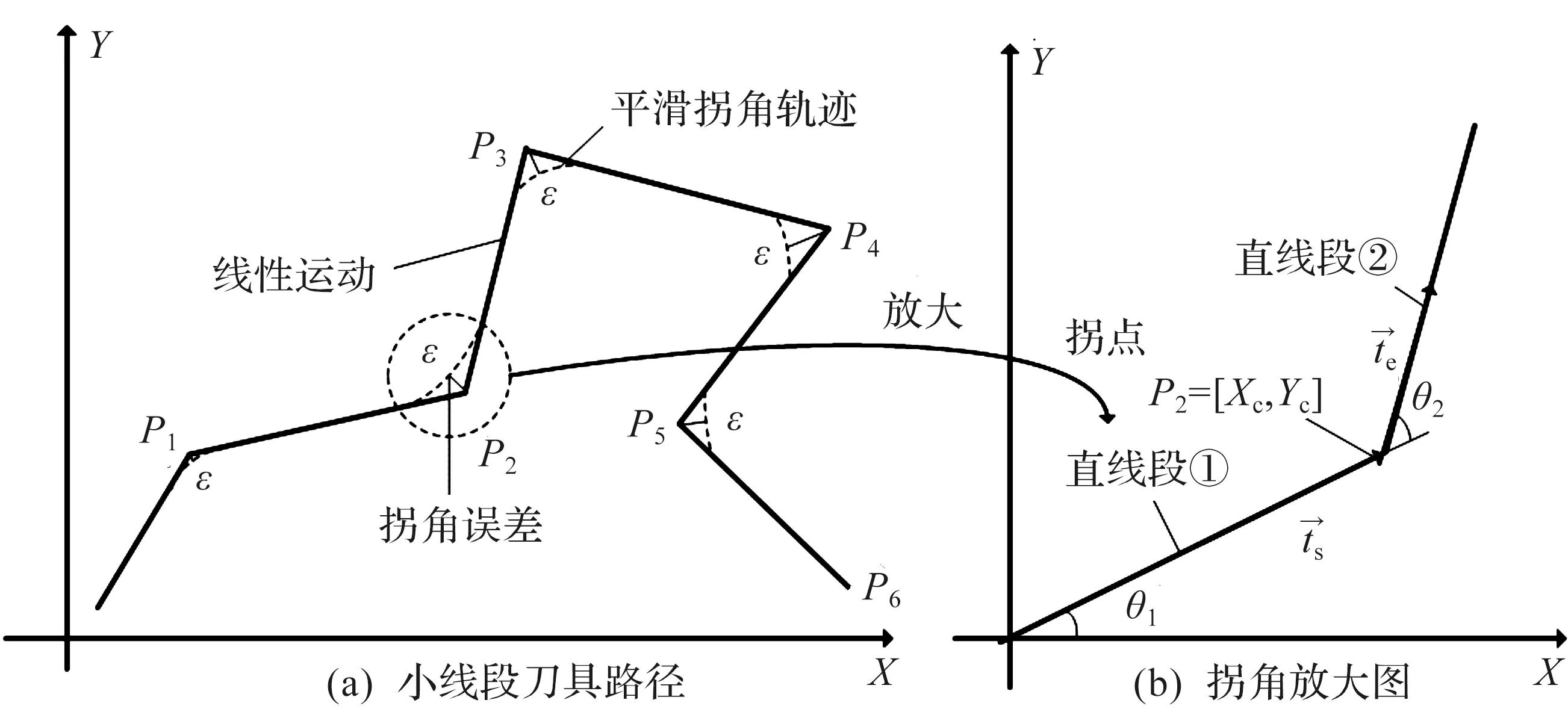
图1 小线段刀具路径图

由图1(a)可观察到:几何形状是位置G0连续的,其允许轴位置指令的连续插值。然而在尖角点处的进给方向不连续地从ts变为te。因此,如果要以恒定的速度走过尖角,就需要无限量的加速来改变角点的轴速度,以致驱动器的能力饱和。机器首先需要在尖角处完全停止,然后继续到下一条直线段。这种方法严重拉长了加工操作的周期时间。目前的技术主要是在指定的转角公差范围内平滑尖角的几何形状,以便机器可以沿着线性分段的刀具路径不停地移动。这种传统的解决方案难以满足实际加工场景,需要采用一种折中的方法,在拐点之前将速度降到一个合适的值,即计算出拐弯处的最大约束速度,以实现速度跟随方向动态的平滑过渡。

笔者提出一种新的策略,即通过设计轴的运动曲线来生成平滑和可控的转角轨迹。如图2所示,刀具以转角速度Vc和加速度Ac接近转角附近,将轴的运动轮廓从进入转角到离开转角平滑地融合在一起,这样就可以连续改变进给方向。在接近驱动器运动性能极限的条件下,如果选择相同的速度Vc和加速度Ac进入转角,那么运动轴就需要在有限的转弯时间Tc内插补,这样会造成在单位切线向量的平分线周围产生对称的转角轮廓,从而与原始尖角几何形状形成最大轮廓误差。

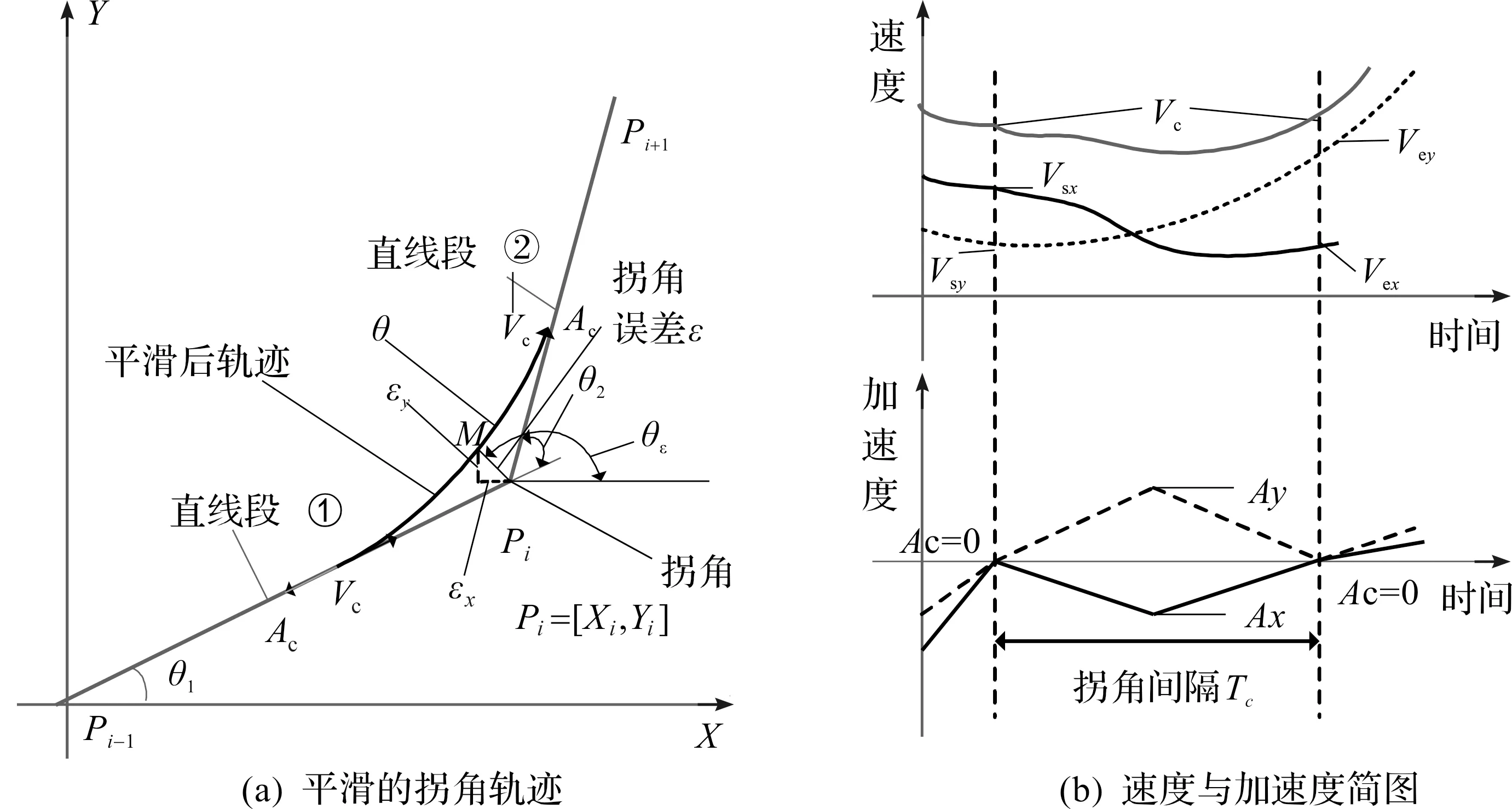
图2 小线段拐角参数示意图

因此,研究的问题就简化为如何确定最大转弯速度和加速度,使转弯轨迹保持在用户指定的转弯误差精度ε内,并利用驱动器的加速度Amax和跳度Jmax的限制,令总转弯周期最小。

1.2 跳度限制加速度描述

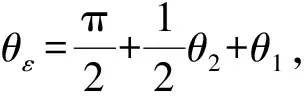
(1)

由式(1)可以得到各轴的拐角处的速度变化计算式为

(2)

当运动到位于拐角的平分线方向上时,此时产生的轮廓误差最大,该中点的位置可以用数学表达式描述为

(3)

同样,结合图2(a)中的几何关系可以得到拐点pi初始运动夹角的关系表达式为

(4)

式中Li为出当前拐点到下一个拐点前的欧式距离。以X轴为例,结合式(1～4)可推导出

(5)

进一步讨论拐角的最大轮廓误差约束,同样以X轴为例,表达式为

(6)

式中:ε为最大轮廓误差;εx为在X轴方向上的轮廓误差。

为保证在轮廓误差足够小的情况,实现刀具的快速切割,按照运动学规律,则需要至少保证一轴的加速度或者速度达到极限值。具体的判断方法:假设Δvx>Δvy,可以得到X轴此时加速度或者跳度值达到了极限值。进一步分情况讨论为

第一种情形:当过渡距离较长,三段速同时存在时,即恒加速阶段存在,X轴的加速度与跳度都达到极限值,即加速度Ax=Amax。由加减速的对称性,可以推出最大拐弯速度Vgw1表达式为

(7)

第二种情形:当过渡距离较短时,速度转接时间较短,而驱动器的加速度较大,有可能恒加速阶段不存在。可得到最大拐弯速度Vgw2表达式为

(8)

1.3 运动学上的自适应转角回滚平滑

为了保证系统在拐点处不完全停止,需要对拐弯处的速度进行限制。若拐点速度小于起跳速度时,以起跳速度为当前拐点的可运行速度;若拐点速度大于起跳速度,则最大拐弯速为Vturnmax=min(Vgw1,Vgw2),依次类推,可前瞻规划整条加工小线段之间拐点上的最大速度。具体拐弯速度约束实现流程如图3所示。

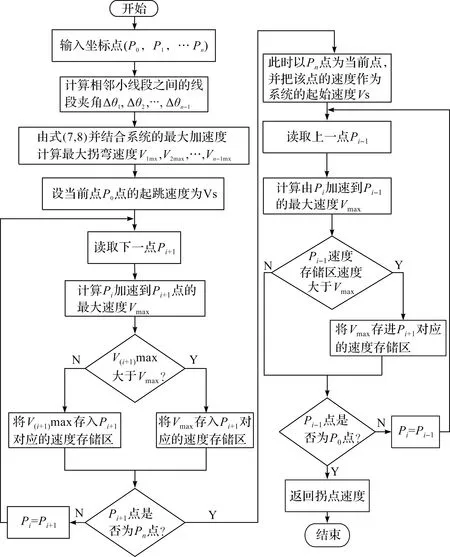
图3 拐弯速度约束实现流程图

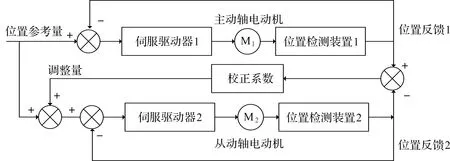
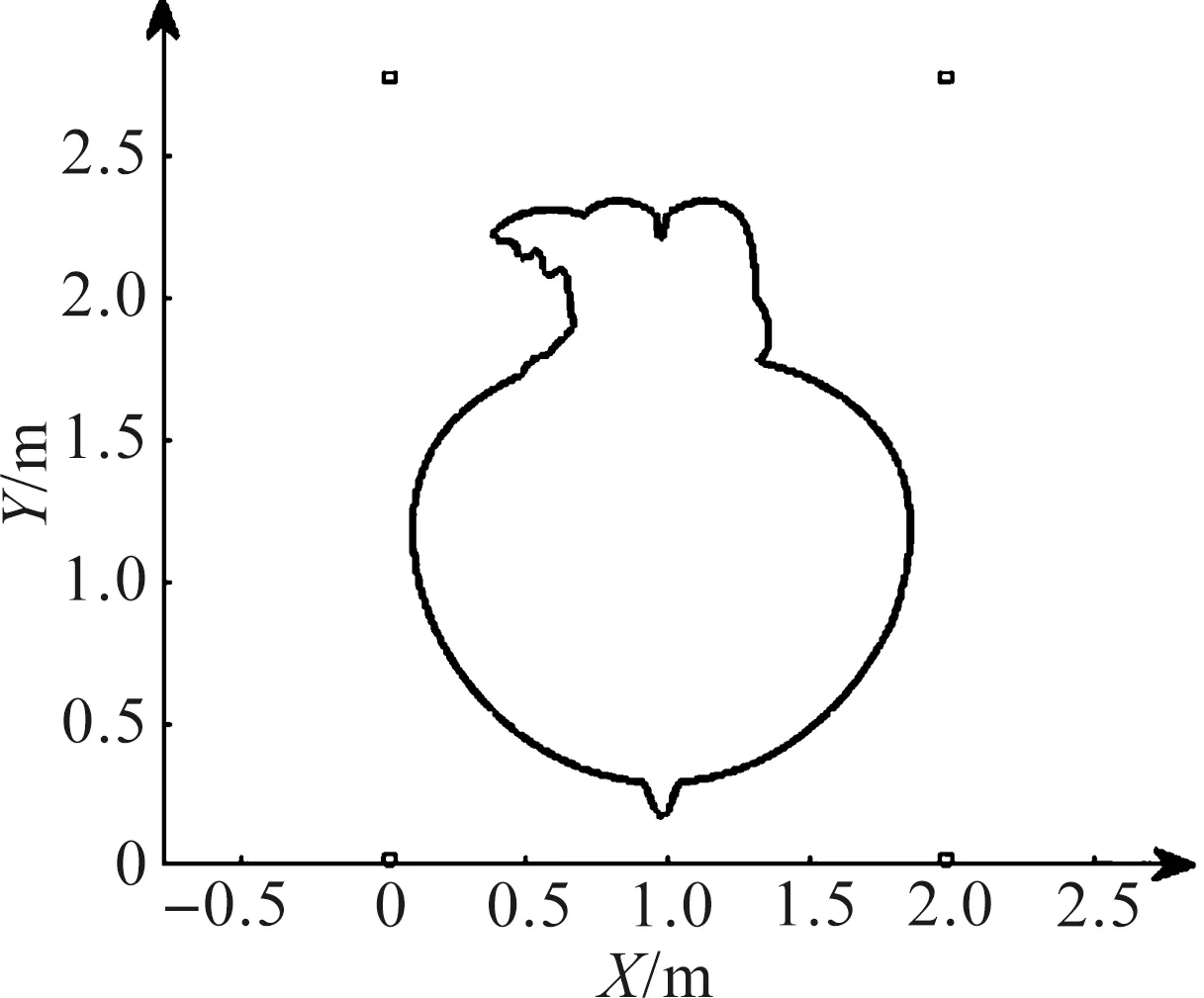
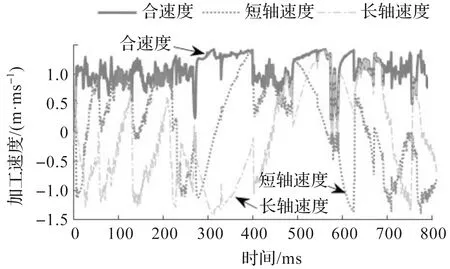
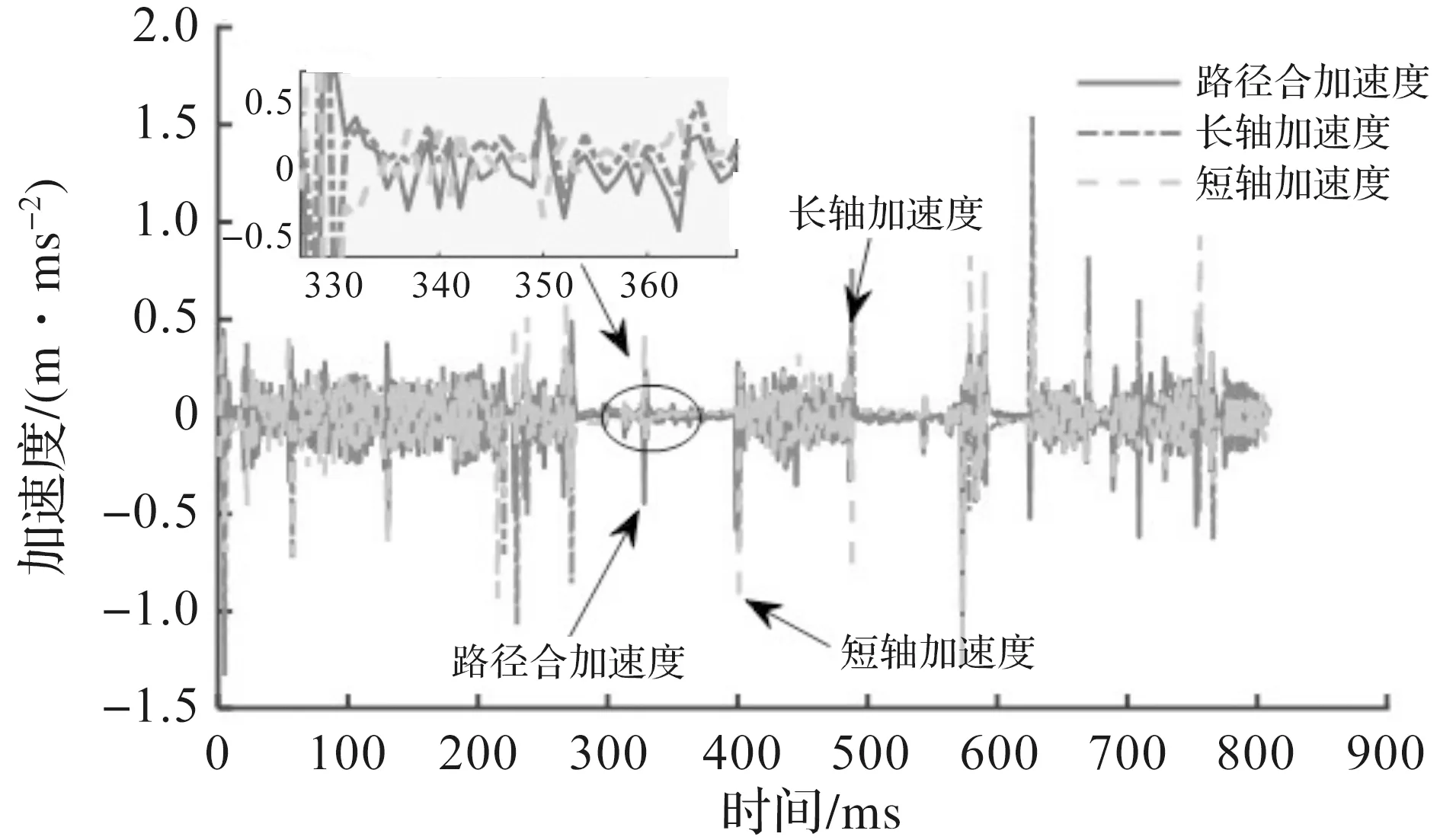
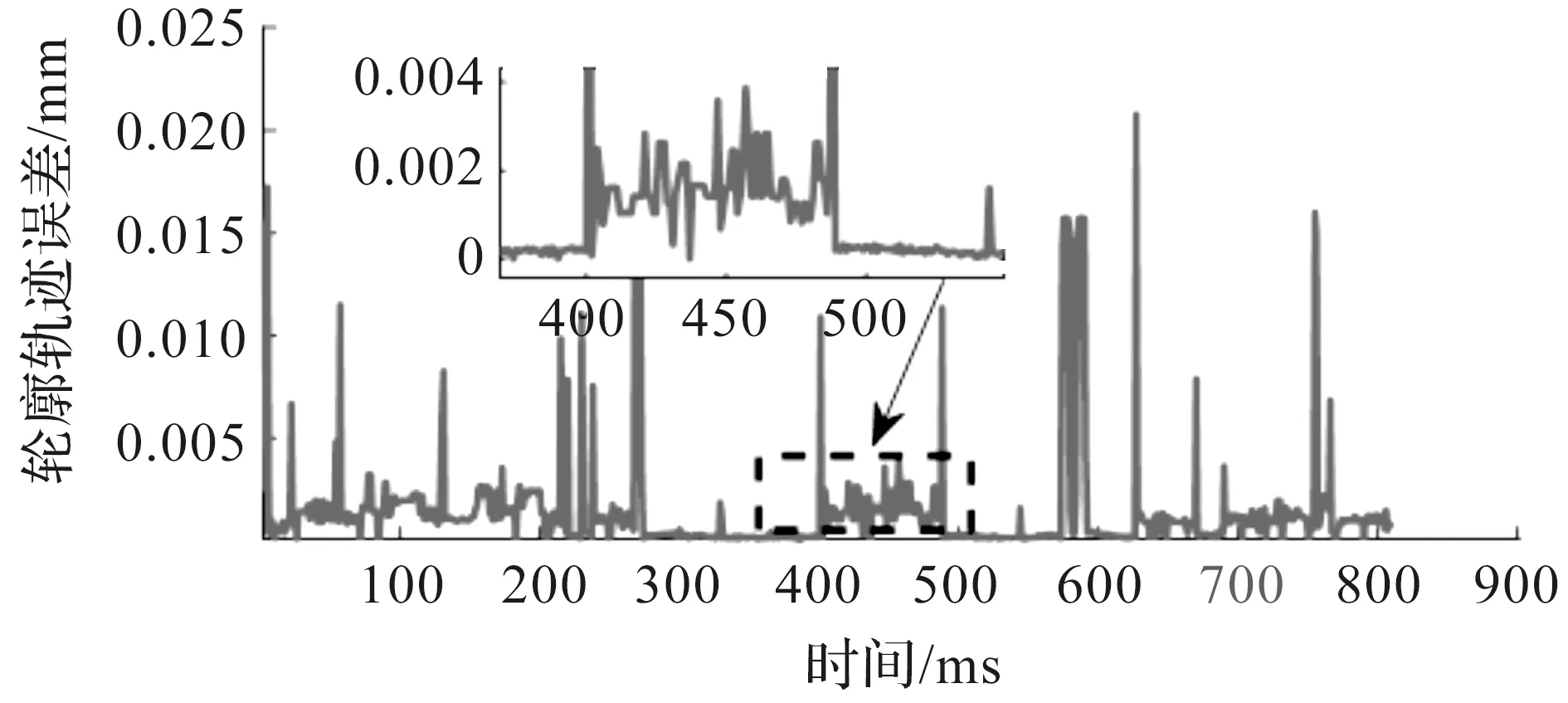
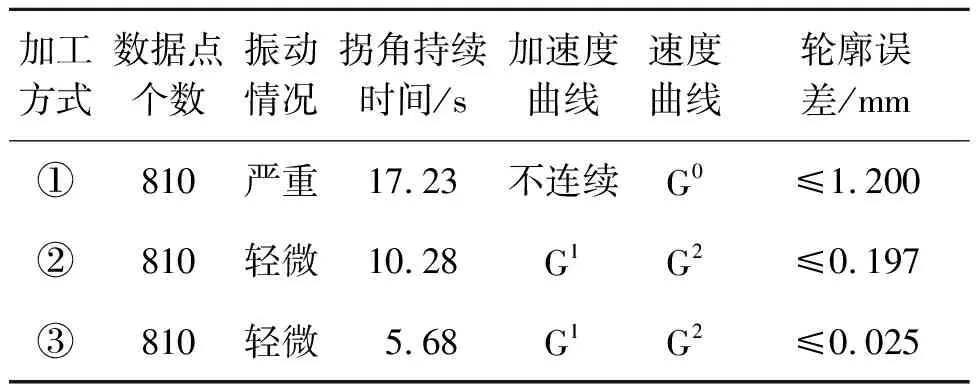
要实现速度在拐角处平滑过渡,除了最大拐弯速度约束,还需要对点与点之间执行的速度进行合理规划。由于线段短,减速距离不够,导致该点越过拐点处设定的最大速度的机械抖动影响了模切精度。因此,需要根据变化的小线段的长度对减加速度再次动态修正,使得最终的拐点速度不会越过设定的速度极限值。假设当前所在的位置移动到下一个位置目标点的长度为L,设定小线段的长度为Lmin,如果L

(9)

式中k为一个常数因子(0≤k≤1),可以根据模切机实际运行状况进行调整。可以将下一个目标点速度作为当前需要运动距离加减速过程中最大的速度。

1.4 双轴同步控制

对于曲线加工路径来说需要两电机轴协作加减速同步运动,即移动导轨的X轴与Y轴,在移动到目标位置的过程中,需要保证两轴位置偏差量始终控制在一个可允许的误差范围内。多轴之间的同步位置控制[10-11],其输出脉冲数和被机械所限制的最大进给速度是确定的,因此可通过软件实现主从轴跟随闭环控制,控制框图如图4所示。

图4 主从同步控制框图

确定主从双轴的脉冲数与脉冲周期的具体方法为

结合项目中使用的实际电机参数(该参数由电机实际运行试验获得),来确定各轴电机S曲线速度表V1,V2,…,Vm,该速度表和给进步长的关系满足Lm=VmT,其中:Lm为模切机最小给进步长表中下标为m时对应的步长值;Vm为速度表中对应下标为m时的速度;T为插补周期。长轴的脉冲个数计算式为

nxi=Txi·Vxi

(10)

根据式(10),考虑到脉冲数只有整数,不存在小数,需要对nxi向下取整得到n′xi,进一步得到X轴实际插补周期为T′xi。同时得到Y轴在这个插补周期内对应脉冲数为nyi,nyi取整数后得到n′yi,对应的周期内存在偏差为ΔTyi,即

ΔTyi=T′xi-Vyin′yi

(11)

为了减小短轴每个插补周期中脉冲数取整而造成的修正累积误差,需要把Y轴每个插补周期中的误差ΔTyi,补偿到下个插补周期Tyi中,即

Tyi=Vyin′yi+ΔTyi-1

(12)

式中:ΔTyi-1为上一个插补周期计算得到的回补插补周期差值,以便用来更新下一个插补周期,可以保证X轴与Y轴的插补时间误差控制在一个脉冲周期内,最大程度地提高插补精度。

根据上述一系列推导计算,可分别得到主从轴脉冲数与脉冲周期,将之存入各自对应的脉冲数与脉冲周期缓冲区,在同步信号来临时,主从双轴分别以一定频率发送脉冲实现对电机的精确插补控制。

2 仿真分析与实验验证

为了对笔者所提出的面向柔性加工的拐角运动策略进行仿真并验证其有效性,搭建的实验软硬件环境:MATLAB R2018b,计算机处理器Intel(R)Core(TM)i5-5200U CPU,运行频率2.20 GHz,内存配置8 G。加工路径如图5所示。

图5 刀具加工路径

刀具实际切割速度以及各轴给进速度曲线如图6所示。限定最大加速度为2 000 mm/s2,双轴给进加速度曲线如图7所示。插补周期为10 ms,允许的最大轮廓误差为0.05 mm。

图6 拐角处给进速度优化后效果

图7 加速度曲线

从仿真图7可以发现:加速度G1连续,有效地降低了电机的频繁启动。为了进一步验证笔者算法的可行性,需要通过长时间在自研控制器测试平台上反复运行测试,平台采用ARM Cortex-M4架构的DSP控制器芯片,其FPU具备高速浮点数计算性能。对其软件设计进行了优化,对给进连续速度曲线,提前进行离散化,便于处理器快速处理。进行测试的平台如图8(a,b)所示,自研控制器主板如图8(c)所示。

图8 嵌入式运动控制系统

试验测试时设定的最大加速度为2 000 mm/s2,最大拐弯速度180 mm/s,给进速度为300 mm/s。复杂图案切割的实际效果如图9所示。

图9 复杂图案切割实际效果图

轮廓误差曲线如图10所示。通过对实际加工点的位置测量与PLT文件中相对应的原始坐标点进行对比发现:X轴与Y轴的精度误差值均在0.025 mm之内。

图10 轮廓误差曲线

实际加工参数指标评价如表1所示。

表1 实际加工参数评价指标

在同等作业条件下,对卡通图片切割测试,其中加工方式①为拐角处速度直接过渡;加工方式②为王勇等[7]所提出的连续拐角高速加工的中点约束算法;加工方式③为柔性加工的拐角运动策略,实现自适应拐角速度平滑。通过对表1中模切机的加工数据分析发现:加工方式②与③均具有加速度曲线、速度曲线连续的优势,机头抖动程度轻微,运行更加稳定。但在加工时间,轮廓误差方面,本运动控制设计与加工策略更具有优势。

3 结 论

笔者所提出的面向柔性加工的拐角运动策略,基于跳度约束解决了拐角与加速度之间耦合关系,同时利用软件优化闭环双轴同步插补,有效地提高了模切机的加工精度。通过仿真与实际加工测试得出:在高速加工连续小线段时,曲线轮廓误差保持在0.025 mm内,加速度曲线满足G1连续,加工时间缩短了13%,因此所研发的标签模切机运动控制器能够满足高速场景下工作稳定、精度高等优势,满足市场应用要求。