襟翼形式对扑翼获能特性影响的对比分析

张 刚，孙晓晶，*

(1. 上海理工大学 能源与动力工程学院，上海 200093；2. 上海市动力工程多相流动与传热重点实验室，上海 200093)

0 引 言

为了应对全球气候变化，实现经济与生态环境的高质量可持续发展，我国大力发展新型能源，加快推进能源向绿色低碳转型。扑翼作为一种可从流体中获取能量且结构简单、环境友好的新型获能装置[1]，近些年受到了研究人员的关注。1981 年Mckinney[2]提出扑翼机的概念并进行了初步实验，此后又有许多研究者对扑翼的特性进行了详细研究。Kinsey等[3-4]探究了空间排列方式对扑翼获能的影响，指出串联布置扑翼有达到高获能效率的潜能。Simpson[5]通过水槽实验探究了不同运动参数对扑翼获能特性的影响，并进一步阐释了扑翼的获能机理。Wang 等[6]也探究了扑翼几何参数，如翼型厚度、弯度、最大厚度位置等，对振荡水翼获能特性的影响。Zhu[7]对缩减频率这一参数进行了系统探究，指出扑翼的获能效率最初随着缩减频率单调增加，达到峰值后，随着频率的进一步增大，获能效率急剧降低。

近年来，为进一步提高扑翼获能效率，主被动控制技术在扑翼上的应用越来越受人们关注。被动控制技术有格尼襟翼[8]、涡发生器[9]等。Zhu等[10]在扑翼不同位置处安装格尼襟翼并进行了数值模拟研究，结果表明安装位置越接近扑翼尾部，格尼襟翼对扑翼获能效率的提升效果越好。Xie 等[11]通过数值模拟的方式探究了格尼襟翼高度对扑翼获能特性的影响，发现当襟翼高度近似为0.003c时，扑翼获能效率的提升幅度最佳。上述研究表明格尼襟翼对扑翼获能效率的提升效果主要是针对低中缩减频率工况，而高缩减频率工况下的提升效果并不明显，甚至获能效率在一定程度会有所下降，只能针对特定状态实施控制。主动控制技术包括环量控制[12]、合成射流[13]、尾缘襟翼[14-15]等。Zhou等[16]提出了一种带尾缘襟翼的扑翼模型，并通过数值模拟的方法证明了当尾缘襟翼长度取0.33c、翼缝宽度取0.001c时，扑翼获能效率的提升效果最好。周大明等[17]的研究结果表明翼型厚度会影响尾缘襟翼扑翼前缘涡的演化，进而影响获能效率。Sun 等[18]指出尾缘襟翼的俯仰振幅和振荡周期对扑翼获能效率的提升有显著影响。上述研究表明尾缘襟翼对扑翼获能效率的提升效果主要是针对中高缩减频率工况，而低缩减频率工况下的效果并不明显。

上述尾缘襟翼的研究主要集中在尾缘襟翼的长度、偏转角度及翼缝宽度等方面，对于不同偏转形式的尾缘襟翼在扑翼获能上的应用，目前的研究十分有限。为进一步改善扑翼获能的气动特性，本文通过数值模拟方法，以NACA0015 对称翼型作为研究对象，选取了4 种不同的尾缘襟翼偏转形式，研究尾缘襟翼偏转形式对扑翼获能效率的影响，并揭示尾缘襟翼偏转形式提高扑翼获能特性的机理。同时本文还探究了尾缘襟翼与格尼襟翼两种不同襟翼控制方式对扑翼获能性能的影响，详细地对比了两种控制方式提高扑翼获能特性的不同机理，找寻较优的可提升扑翼获能器性能的控制方式。

1 计算模型与验证

1.1 扑翼运动模型

图1 为扑翼的升沉运动和俯仰运动模型示意图。其中，c为翼型弦长；U∞为来流速度；h(t)是翼型在竖直方向上的位移；h0代表升沉幅值；θ(t)为俯仰角度，表示来流方向与翼型弦线方向的夹角；θ0代表俯仰幅值；d为扑翼扫掠面积，在二维中即为翼型尾缘扫掠高度。

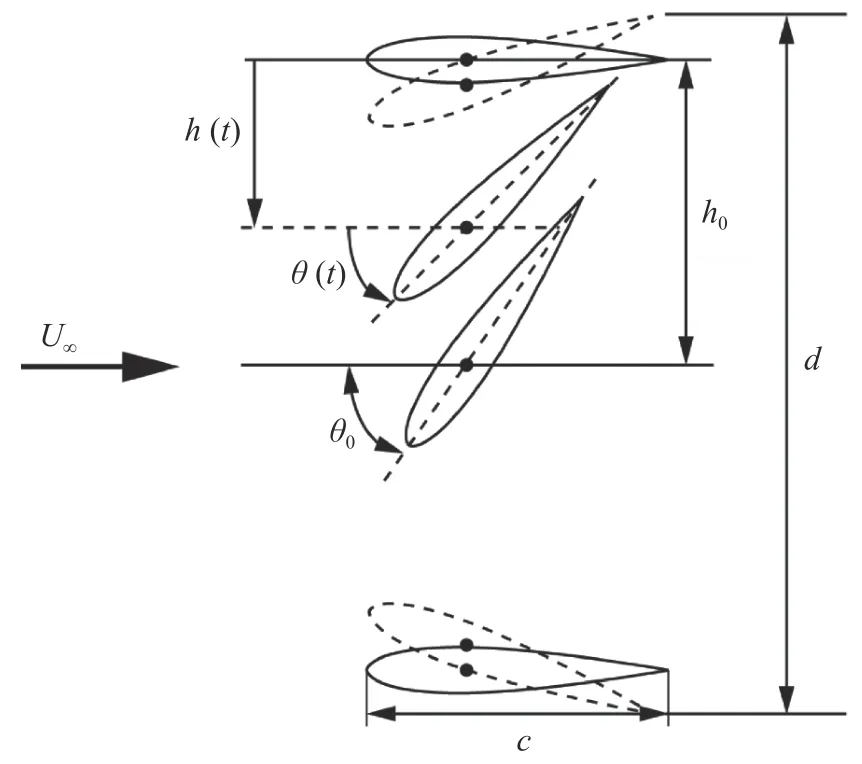
图1 扑翼运动模型示意图Fig. 1 Sketch of the heave and pitch motions of a flapping foil

扑翼升沉和俯仰运动的运动方程式可分别表示为：

其中，f为扑翼俯仰频率，t为时间，φ为升沉运动与俯仰运动之间的相位角。本文取相位角φ= 90°，此时运动方程又可表示为：

所以，扑翼瞬时升沉速度Vy(t)与扑翼瞬时俯仰角速度ω(t)为：

流体作用于扑翼的力包括两部分，分别是升沉力Y和俯仰力矩M。因此平均获能功率系数为无量纲化的单个周期的升沉力做功PY与俯仰力矩做功Pθ之和[1,19-20]：

式中，为平均升沉力功率系数；为平均俯仰力矩功率系数；CY为升沉力系数，为俯仰力矩系数，为流体密度；T为翼型扑动周期。

一个周期内扑翼从流体中提取的能量与来流中蕴含的总能之比即为扑翼获能效率η：

本文所提出的带格尼襟翼（被动式）扑翼形式示意图见图2。格尼襟翼是一种典型的被动控制技术，具有结构简单、无需额外的能量输入等特点。图中，格尼襟翼位于NACA0015 对称翼型的尾端，垂直于翼型的中心线，lg为格尼襟翼长度。由于没有额外的转动机构，格尼襟翼扑翼获能效率η依然采用公式（6）计算。本文所提出的另一种带尾缘襟翼（主动式）扑翼形式示意图见图3。尾缘襟翼作为一种常见的主动控制方式，目前在单一翼型及扑翼上已有相关的应用研究。图中，β0为尾缘襟翼偏转角度幅值，lt为尾缘襟翼长度，w为翼缝宽度，翼型采用NACA0015 对称翼型。

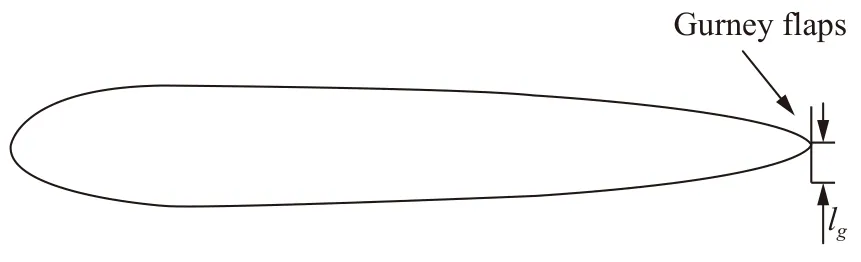
图2 带格尼襟翼（被动式）扑翼形式示意图Fig. 2 Sketch of a flapping foil with passive Gurney flaps

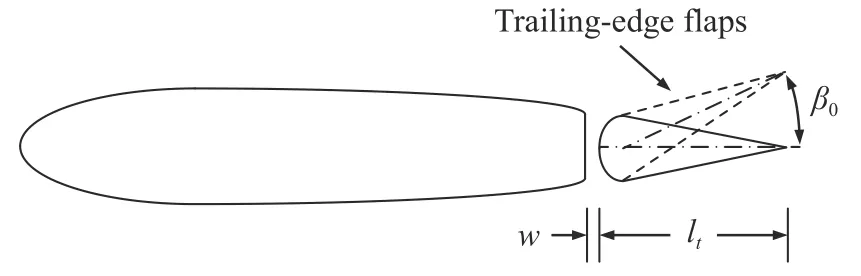
图3 带尾缘襟翼（主动式）扑翼形式示意图Fig. 3 Sketch of a flapping foil with active trailing-edge flaps

对于尾缘襟翼扑翼，由于附加了尾缘襟翼自身的俯仰运动，因此在计算扑翼的总获能效率时，其俯仰运动对自身俯仰轴产生的俯仰力矩做功也应一并计入。定义尾缘襟翼的俯仰力矩功率系数为CPβ，计算公式如下[16,18]：

其中，CMt为尾缘襟翼俯仰力矩系数，尾缘襟翼瞬时俯仰力矩系数Mt为尾缘襟翼偏转轴的俯仰力矩，Mt(t)为尾缘襟翼偏转轴的瞬时俯仰力矩；ωt(t)为尾缘襟翼瞬时偏转角速度，ωt(t)=2πfβ0cos(2πft)。故尾缘襟翼扑翼的获能效率计算公式为：

1.2 边界条件与计算网格

本文构建的计算域如图4 所示。采用结构−非结构的网格布局：计算域Ⅰ为非结构动网格域，半径为3c，将内部翼型周围的非结构动网格域设置为变形域，通过网格重构以实现扑翼的升沉、俯仰运动，其中对扑翼前缘与尾缘处的网格进行局部加密，使y+处于1 附近；计算域Ⅱ为静止的结构网格域，半径为30c，计算域Ⅰ和Ⅱ通过交界面（interface）连接，进出口边界条件分别采用速度入口（velocity inlet）与压力出口（pressure outlet）。方程的求解采用压力-速度耦合算法；方程离散时，所有空间项和时间项均采用二阶精度格式；计算中数值的处理采用双精度；方程求解结果的收敛精度为1×10−6。

图4 扑翼边界条件及局部网格示意图Fig. 4 Boundary conditions and local mesh of a flapping wing

2 网格模型与数值模型可靠性验证

为保证数值模拟的准确性，在3 组工况参数下分别对网格量、时间步长与湍流模型对计算结果的无关性进行验证。本文选用NACA0015 对称翼型作为研究对象，工质为液态水。其中：弦长c= 0.24 m，俯仰轴位置xp/c= 1/3，来流速度U∞= 2 m/s，雷诺数Re=5×105，升沉幅值h0=c，俯仰幅值θ0= 75°，升沉运动与俯仰运动之间的相位角φ= 90°。在上述参数下进行了18 组数值模拟，验证结果如表1。从表1 中可以看出，当网格量取2×105、时间步长取T/1500 时，可以在耗时较少的情况下得到精度较高的计算结果。对于4 种湍流模型对扑翼获能的影响，可以从两个方面进行考虑：首先，从获能效率来看，不同湍流模型对获能效率的影响较小，四种湍流模型之间获能效率相对误差均小于1%；其次，不同湍流模型下扑翼的最大升沉力系数平均水平力系数以及最大俯仰力矩系数之间的相对误差也小于1%。考虑到计算精度及资源消耗，当网格数取2×105、时间步数取T/1500、湍流模型取Spalart-Allmaras（S-A）时，可在耗时较少的情况下得到精度较高的计算结果，因此将其作为后续模拟计算的基准。

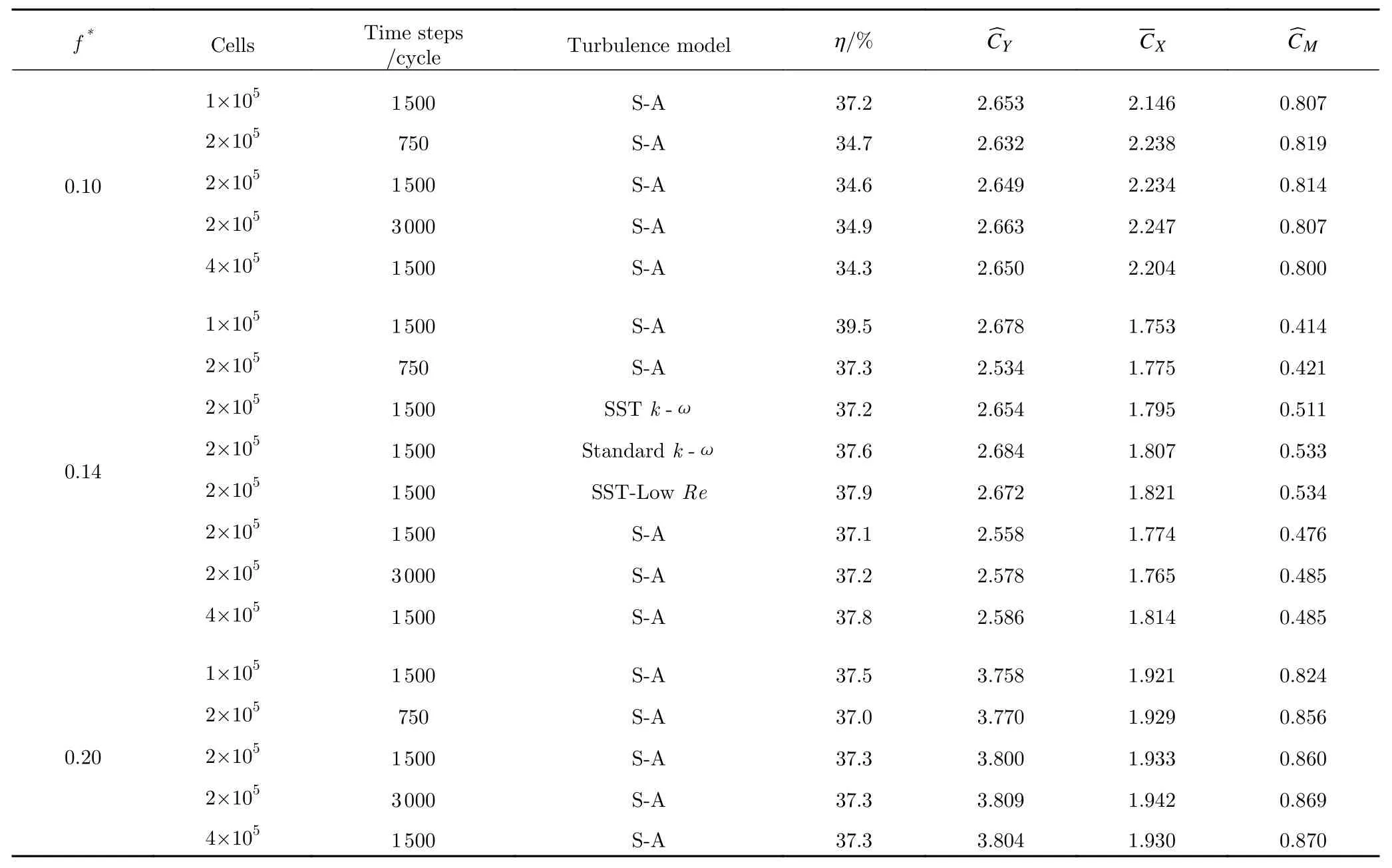
表1 网格数目、时间步数及湍流模型无关性验证Table 1 Sensitivity studies of mesh, time step and turbulence model

为了充分验证本文数值模型的可靠性与结果的准确度，首先采用经典文献[21]中Kinsey 的实验模型对传统扑翼获能特性进行模拟，并以文献[21]中的实验数据为依据进行误差分析；然后将本文得到的数值结果与文献[3、22、23]中Kinsey、He 的数值模拟结果进行对比分析，如图5 所示。由图可见，本研究的升沉力系数模拟结果与Kinsey、He 的模拟结果十分接近，同时获能效率也与Kinsey、He 的二维模拟结果较为接近。综上，模拟所采用的网格及计算方法等可以认为是有效的。

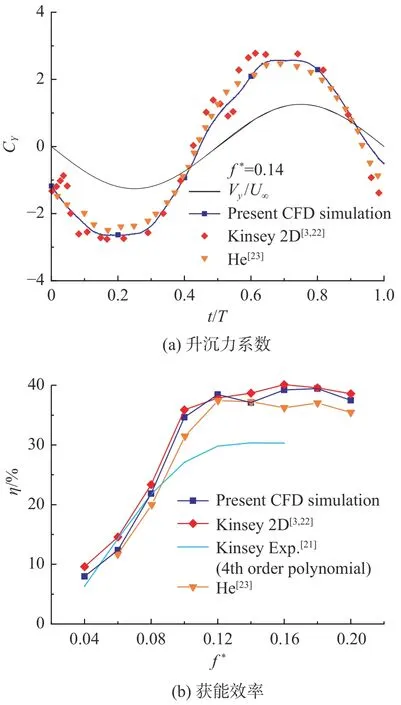
图5 本文数值模拟结果与文献中的实验及数值结果对比Fig. 5 Comparison between present CFD simulations and published results

3 结果与讨论

3.1 尾缘襟翼偏转形式对扑翼获能的影响

本文选取了4 种不同的尾缘襟翼偏转形式，即向压力面连续偏转式（towards pressure side, TP）、向吸力面连续偏转式（towards suction side, TS）、向压力面偏转-静止-偏转式（oscillating-static-oscillating, OSO）以及静止-向压力面偏转-静止式（static-oscillating-static,SOS），以研究尾缘襟翼偏转形式对扑翼获能效率的影响。4 种偏转形式的运动方程分别如下：

TP 式：

TS 式：

OSO 式：

本文尾缘襟翼具体参数选取如下：偏转角度幅值β0= 30°，襟翼长度与翼型弦长之比lt/c= 0.33，翼缝宽度与弦长比w/c= 0.001，缩减频率的范围取0.08～0.22；运用二维数值模拟计算4 种偏转形式的尾缘襟翼扑翼获能效率，结果如图6 所示。可以看出，襟翼向压力面偏转的控制策略的获能效果明显优于向吸力面偏转的情况。其中，向吸力面偏转导致了扑翼的获能效率随缩减频率增大而快速降低，在高缩减频率下则出现了负效率的情况，意味着扑翼的受力方向发生了改变，从获能状态转为推进状态；而向压力面偏转的形式中以连续偏转的TP 式效果最优。本文选取4 组控制策略在获能效率差异较大的f* =0.18 工况下，考察尾缘襟翼偏转形式对扑翼获能特性的影响。

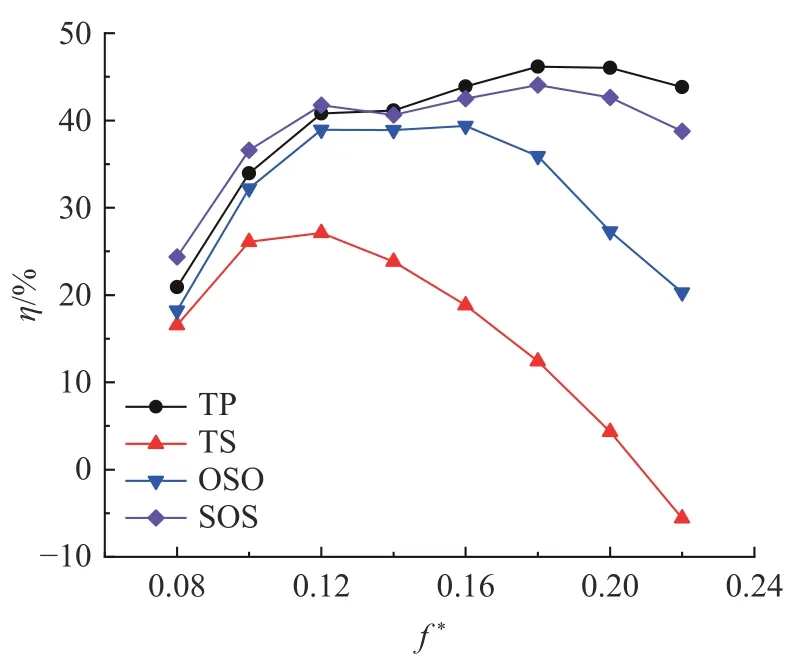
图6 尾缘襟翼偏转形式对扑翼获能效率的影响Fig. 6 Effect of the deflection form of the trailing-edge flap on the energy-harvesting efficiency

4 种偏转形式尾缘襟翼扑翼的升沉力系数、俯仰力矩系数及其功率系数如图7 所示。从升沉力方面来看，尾缘襟翼向压力面偏转时扑翼受到的升沉力远大于向吸力面偏转所受的升沉力；OSO 式与SOS 式则均在其偏转时刻内使扑翼升沉力得到了提高。由于SOS 式襟翼偏转时刻与升沉速度最大时刻（t/T=0.25、0.75）重合度较高，故其升沉力做功高于OSO式；而TP 式全程均在向压力面偏转，因此采用该种方式偏转的扑翼的升沉力最高、做功最多。从俯仰力矩来看，襟翼向吸力面偏转有利于提高俯仰力矩方向与俯仰角速度的同步性，故向吸力面偏转时扑翼的俯仰力矩产生正功最多；三种向压力面偏转的控制策略则均会使俯仰力矩产生负功，其中OSO 式由于在扑翼俯仰阶段（t/T= 0、0.50）使襟翼快速偏转，因此产生了最大的俯仰力矩负功。总体来看，由于扑翼获能过程中升沉力做功占比更大，因此向压力面偏转更有利于提升扑翼获能效率，其中连续偏转的TP 式控制策略最优。

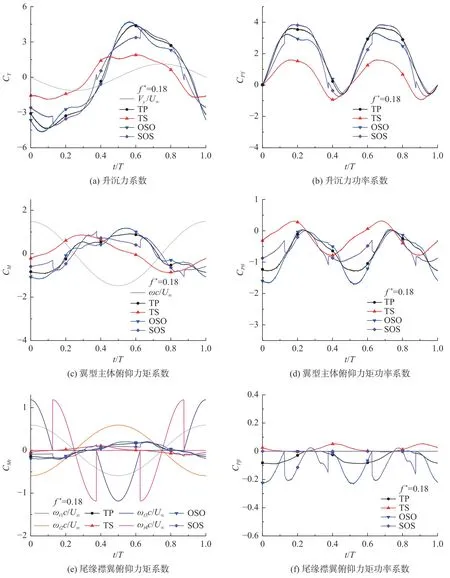
图7 不同尾缘襟翼偏转形式的扑翼在一个运动周期内的升沉力、俯仰力矩及功率系数曲线（f＊ = 0.18）Fig. 7 Variations of heaving forces, pitching moments, and energy-harvesting coefficients of a flapping wing with different deflection forms of the trailing-edge flap in one motion cycle (f＊ = 0.18)

由图7 可知，扑翼的升沉力系数、俯仰力矩系数及其功率系数曲线呈对称分布，因此只需研究扑翼在t/T= 0～0.5 时段内的升沉俯仰运动即可。故下面选取俯仰力矩与升沉力做功较大的t/T= 0.05、0.25 时刻，结合扑翼的涡量、压力云图分析襟翼偏转形式对流场的影响。如图8，t/T= 0.05 时，TP 式与OSO 式襟翼都向压力面偏转，对压力面流体起到了阻滞作用，使得尾缘上表面处产生了较大的压力，阻碍了扑翼此时的逆时针俯仰运动，此时两种方式的压强分布面积最大；TS 式由于襟翼向吸力面偏转，减缓了扑翼下表面流体的流速，削减了上下表面阻碍俯仰运动进行的压力分布，有利于俯仰力矩产生正功；SOS 式襟翼相对扑翼主体保持静止，因此此时没有明显的控制效果。t/T= 0.25 时，TS 式向吸力面偏转，使得吸力面尾缘处产生了明显的正压区，破坏了翼型两侧有利于升沉运动的压力分布，因此此时升沉力最小；其余三种控制方式此时的襟翼都处于压力面偏转状态，有利于提升扑翼两侧压差。通过式（15）可知，OSO 式襟翼的偏转角度在t/T= 0.125 时刻即已达到幅值状态，但其压差分布明显弱于其余两者，这说明了可能即使偏转角度提早达到幅值也无益于长久地保持升沉力的幅值状态。

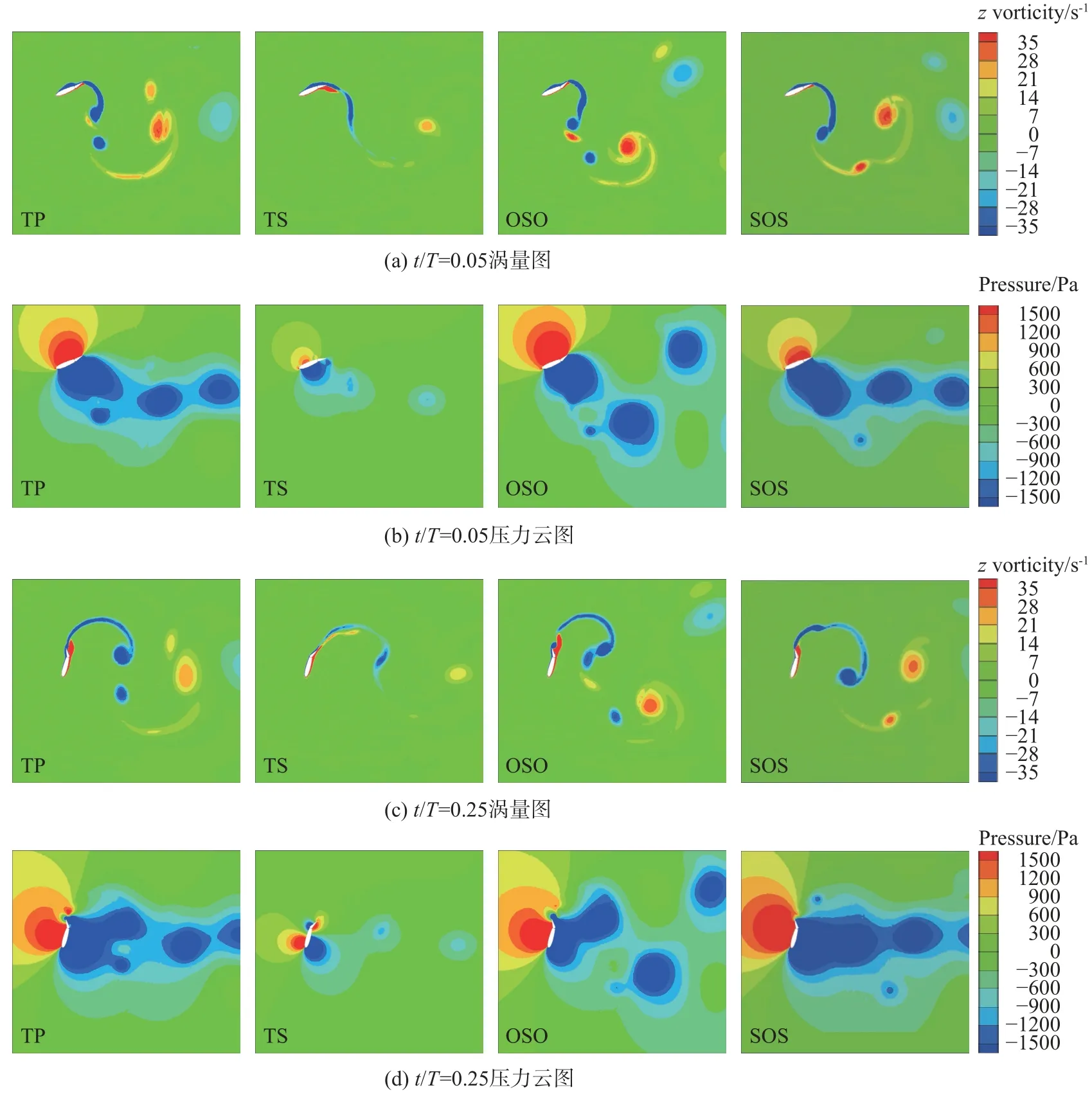
图8 一个运动周期中不同尾缘襟翼偏转形式下扑翼的涡量及压力云图（f＊ = 0.18）Fig. 8 Instantaneous vorticity and pressure contours around flapping wings with different deflection forms of the trailing-edge flap in one motion cycle (f＊ = 0.18)

3.2 两种襟翼形式对扑翼获能影响的对比分析

本节主要探讨尾缘襟翼和格尼襟翼两种襟翼控制方式对扑翼获能性能的影响。尾缘襟翼（主动式）扑翼模型如图3 所示，选取偏转形式为TP 式的尾缘襟翼，尾缘襟翼偏转角度幅值β0= 30°，襟翼长度与翼型弦长之比lt/c= 0.33，翼缝宽度与弦长之比w/c=0.001。格尼襟翼（被动式）扑翼模型如图2 所示，格尼襟翼长度与翼型弦长之比lg/c= 0.02。缩减频率范围取0.08～0.22，进行二维数值模拟。

图9 给出了不同缩减频率下尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼获能效率的对比图。从图中可以看出，尾缘襟翼扑翼获能效率的峰值明显高于格尼襟翼扑翼与原始扑翼获能效率的峰值。在低缩减频率下，相较于原始扑翼，格尼襟翼扑翼的获能效率有所提升，而尾缘襟翼扑翼的获能效率出现了轻微的下降；在中缩减频率下，尾缘襟翼扑翼与格尼襟翼扑翼的获能效率均得到提升，且提升效果基本一致。在高缩减频率下，尾缘襟翼扑翼的获能效率进一步得到提升，而格尼襟翼扑翼的提升效果不明显，甚至随着缩减频率的提高，扑翼的获能效率出现了一定程度上的降低。下文选取缩减频率f* = 0.10、0.18 作为特征频率工况，分析不同缩减频率下尾缘襟翼和格尼襟翼对提升扑翼获能效率的不同机理。

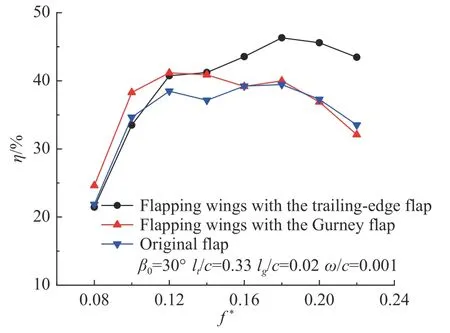
图9 尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼获能效率的对比图Fig. 9 Comparison of energy-harvesting efficiency between flapping wings with the trailing-edge flap,gurney flap, and original flap

3.2.1 缩减频率f* = 0.10

图10 为缩减频率f* = 0.10 时，尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼的升沉力系数、俯仰力矩系数及其功率系数在一个运动周期内的变化曲线。从升沉力方面来看，尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼的升沉力与升沉速度保持较好的同步性，因此升沉力在一个运动周期内做正功。在整个运动周期内，格尼襟翼扑翼受到的升沉力大于尾缘襟翼扑翼与原始扑翼的升沉力，因而格尼襟翼扑翼升沉力做功大于尾缘襟翼扑翼与原始扑翼升沉力做功。从俯仰力矩来看，尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼的俯仰力矩在3/4 个周期内与俯仰角速度不同步，并且不同步时间段内尾缘襟翼扑翼的俯仰力矩大于格尼襟翼扑翼与原始扑翼的俯仰力矩，因此一个运动周期内尾缘襟翼扑翼负功贡献更多。结合升沉力做功系数与俯仰力矩做功系数来看，格尼襟翼扑翼的获能功率系数更大。

图10 尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼在一个运动周期内的升沉力、俯仰力矩及功率系数曲线图（f＊ = 0.10）Fig. 10 Variations of heaving forces, pitching moments, and energy-harvesting coefficients of flapping wings with the trailing-edge flap,Gurney flap, and original flap in one motion cycle (f＊ = 0.10)

由图10 还可知，扑翼的升沉力系数、俯仰力矩系数及其功率系数曲线呈对称分布，因此只需研究扑翼在t/T= 0～0.5 时段内的升沉俯仰运动即可。图11 和图12 分别为缩减频率f* = 0.10 时，一个运动周期内尾缘襟翼扑翼、格尼襟翼扑翼和原始扑翼在不同时刻时，瞬态流场的涡量云图对比和压力云图对比。当t/T= 0.15 时，与原始扑翼相比，格尼襟翼扑翼上下表面的正压区和负压区均有所增强，并且由于格尼襟翼的存在，在压力面尾部出现了小范围负压区；而尾缘襟翼扑翼两侧有更大范围的正压区和负压区，升沉力有所提高，并且在尾缘襟翼处开始出现分离涡。当t/T= 0.25 时，扑翼继续下俯运动，格尼襟翼扑翼尾部的负压区基本消失，升沉力得到提高；与原始扑翼相比，尾缘襟翼扑翼因为扑翼俯仰角和尾缘襟翼偏转角同时达到最大，襟翼处出现了明显的分离涡，而尾缘襟翼向压力面的连续偏转，使压力面的尾部出现负压区，在一定程度上削弱了升沉力。当t/T= 0.35 时，与原始扑翼相比，格尼襟翼扑翼尾部的分离涡强度更大，并且襟翼的存在增大了翼型上下两侧的压力差，从而导致升沉力所做的正功增加，这一点可以在图10 中得到验证。而对于尾缘襟翼扑翼，由于襟翼偏转角减小，尾缘压力面的负压区减小，从而使升沉力和俯仰力矩均得到提高，并且分离涡开始出现脱落的迹象。当t/T= 0.45 时，扑翼将下俯至水平位置，俯仰速度处于峰值，俯仰力矩做功占功率输出的主要部分。与原始扑翼相比，格尼襟翼扑翼由于襟翼存在，卸除了翼型压力面表面的负压区，增强了升沉力做功。而尾缘襟翼扑翼因为襟翼偏转角的持续减小，增大了翼型压力面表面的负压区，削弱了俯仰力矩产生的正功。

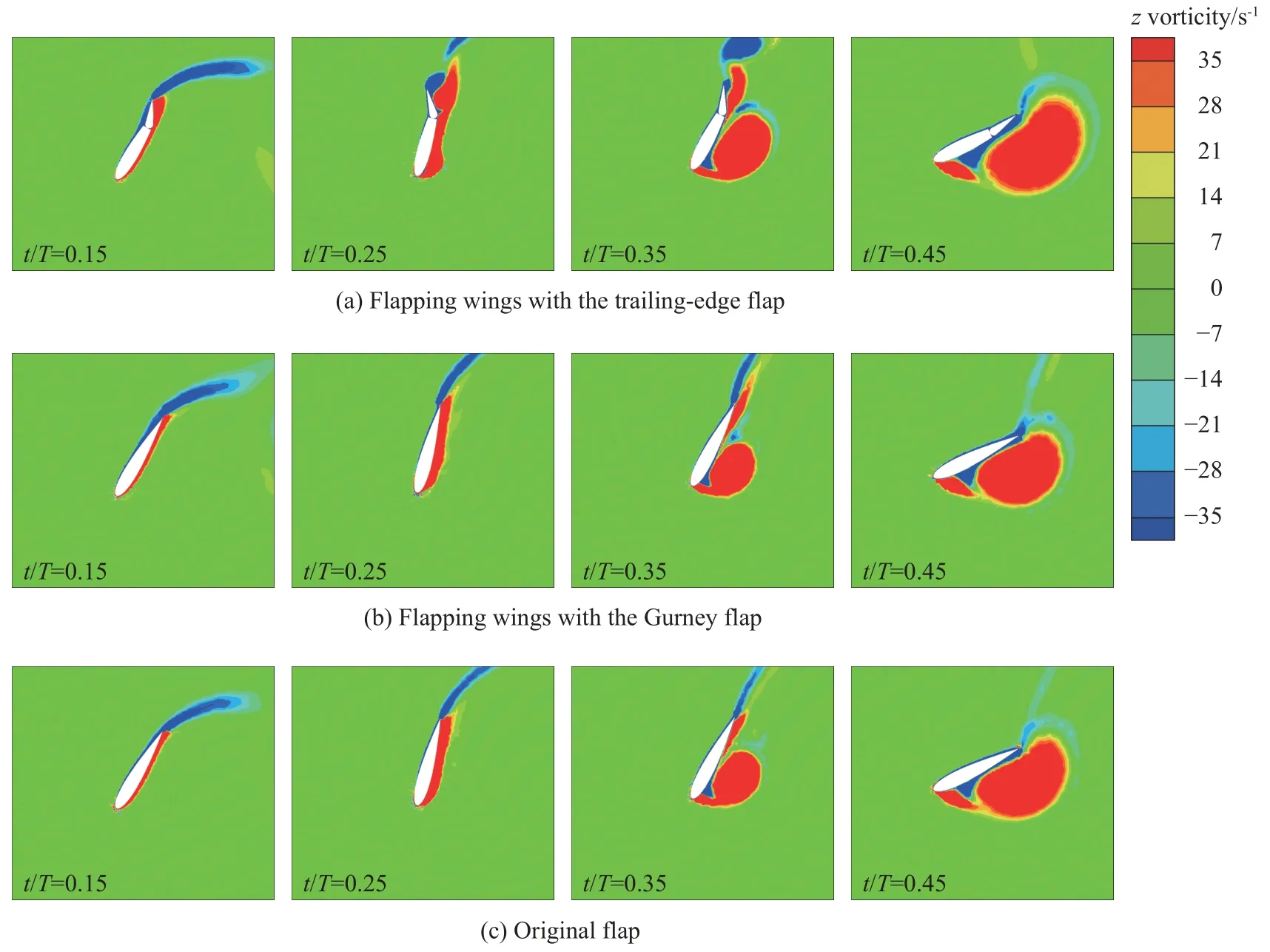
图11 一个运动周期内尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼在不同时刻时瞬态流场的涡量云图对比（f＊ = 0.10）Fig. 11 Temporal evolutions of vorticity contours around flapping wings with the trailing-edge flap, Gurney flap,and original flap in one motion cycle (f＊ = 0.10)

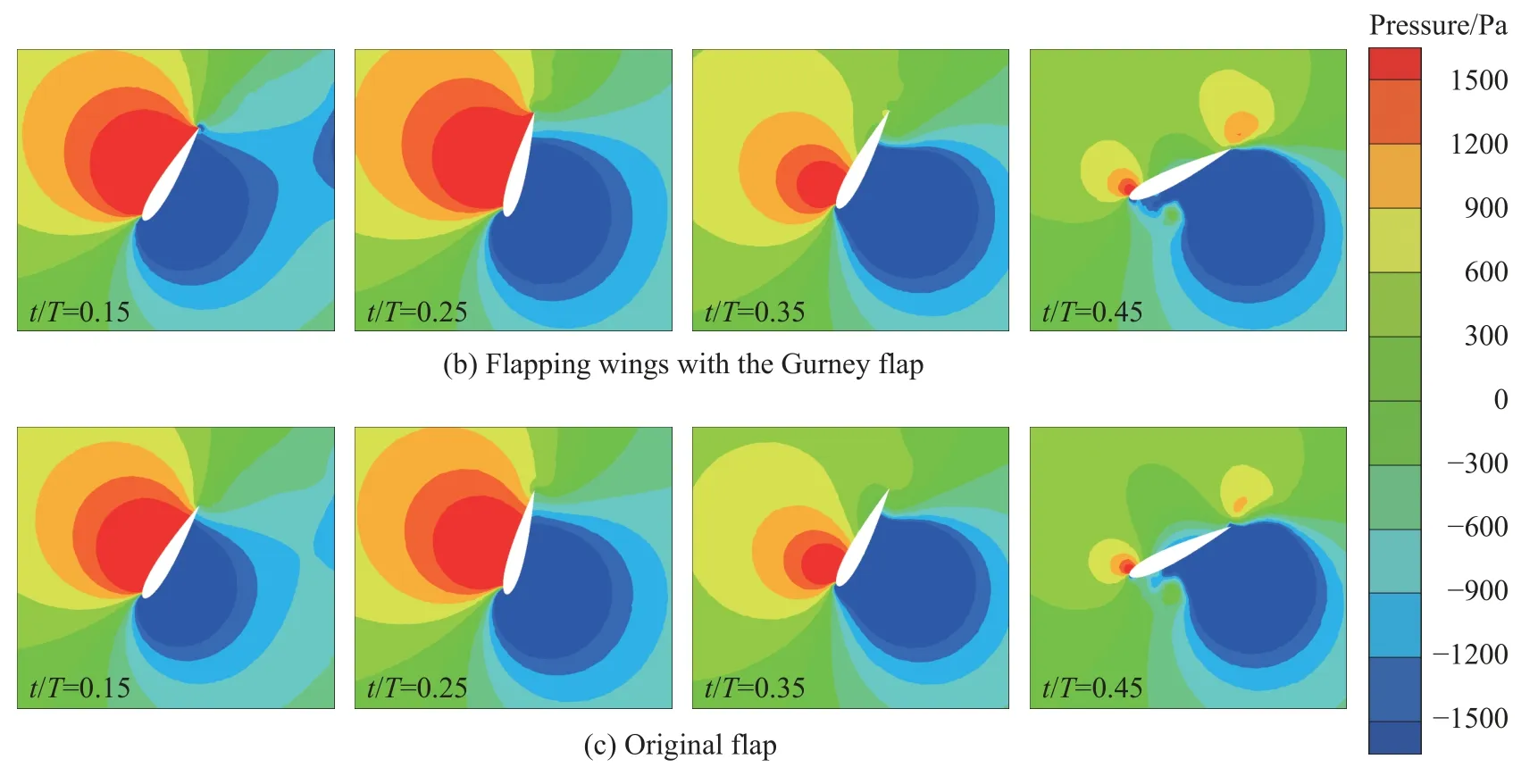
图12 一个运动周期内尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼在不同时刻时瞬态流场的压力云图对比（f＊ = 0.10）Fig. 12 Temporal evolutions of pressure contours around flapping wings with the trailing-edge flap, Gurney flap,and original flap in one motion cycle (f＊ = 0.10)

3.2.2 缩减频率f* = 0.18

图13 为缩减频率f* = 0.18 时，尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼的升沉力系数、俯仰力矩系数及其功率系数在一个运动周期内的变化曲线。从升沉力方面来看，尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼的升沉力在3/4 个周期内与升沉速度保持同步，因此升沉力在3/4 个周期内做正功；剩下的1/4 个周期，由于升沉力与升沉速度不同步，所以尾缘襟翼扑翼、格尼襟翼扑翼和原始扑翼均会产生负功。尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼的差异之处是尾缘襟翼扑翼较原始扑翼，升沉力产生的负功减少，而格尼襟翼扑翼较原始扑翼，升沉力产生的负功增加。这些差异的原因是尾缘襟翼增强了扑翼升沉运动与升沉力方向的同步性，而格尼襟翼扑翼则削弱了扑翼升沉运动与升沉方向的同步性。从俯仰力矩来看，尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼的俯仰力矩在一个运动周期内与俯仰角速度不同步，所以俯仰力矩始终做负功。尾缘襟翼扑翼与格尼襟翼扑翼的差异之处在于达到俯仰力矩峰值的时刻不一致，尾缘襟翼扑翼有两个俯仰力矩峰值，导致一个周期内负功贡献更多，又因为升沉力做功占功率输出的主要部分，因此尾缘襟翼扑翼的获能功率系数得到了提升。格尼襟翼扑翼虽然只有一个俯仰力矩峰值，但升沉力产生的负功更多，所以格尼襟翼扑翼的获能功率系数没有得到进一步提升。

图13 尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼在一个运动周期内的升沉力、俯仰力矩及功率系数曲线图（f＊ = 0.18）Fig. 13 Variations of heaving forces, pitching moments, and energy-harvesting coefficients of flapping wings with the trailing-edge flap,Gurney flap, and original flap in one motion cycle (f＊ = 0.18)

图14 和图15 分别为缩减频率f* = 0.18 时，一个运动周期内尾缘襟翼扑翼、格尼襟翼扑翼和原始扑翼在不同时刻时，瞬态流场的涡量云图对比和压力云图对比。通过与图11 和图12 对比可知，格尼襟翼扑翼较原始扑翼涡量强度和压强基本保持一致，这些流场特征印证了上文对格尼襟翼扑翼获能效率没有提升的做功系数曲线的分析。而对于尾缘襟翼扑翼，因为缩减频率的提高，扑翼表面的涡量强度有所增强，从而导致了更大范围的压力区，所以尾缘襟翼扑翼获能效率得到进一步提升。

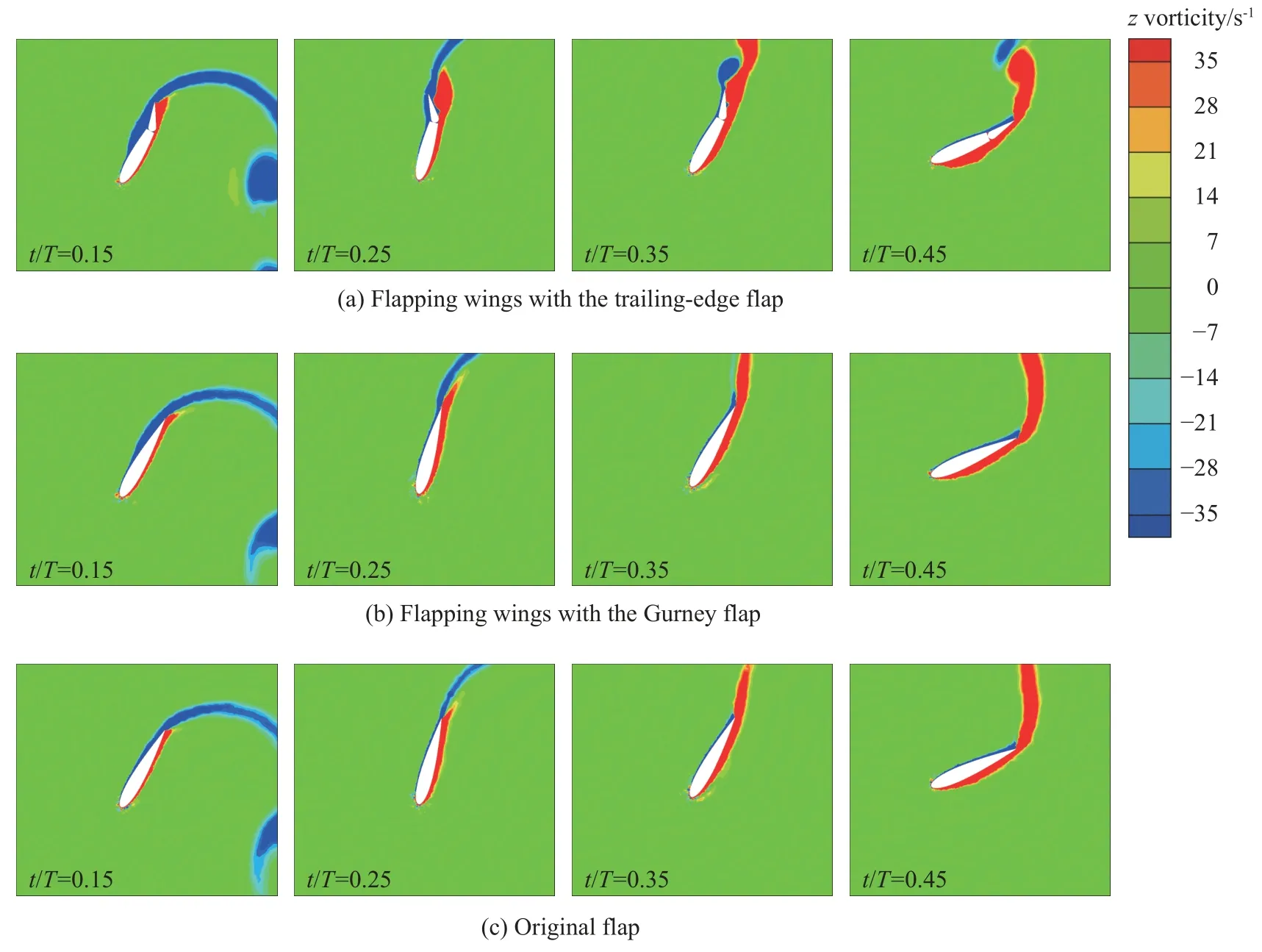
图14 一个运动周期内尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼在不同时刻时瞬态流场的涡量云图对比（f＊ = 0.18）Fig. 14 Temporal evolution of vorticity fields around flapping wings with the trailing-edge flap, Gurney flap,and original flap in one motion cycle (f＊ = 0.18)

图15 一个运动周期内尾缘襟翼扑翼、格尼襟翼扑翼与原始扑翼在不同时刻时瞬态流场的压力云图对比（f＊ = 0.18）Fig. 15 Temporal evolution of pressure contours around flapping wings with the trailing-edge flap,Gurney flap, and original flap in one motion cycle (f＊ = 0.18)

4 结 论

本文以NACA0015 对称翼型为基础，建立了尾缘襟翼扑翼获能器和格尼襟翼扑翼获能器模型，采用基于动网格技术的瞬态数值计算方法，在弦长c=0.24 m、来流速度U∞= 2 m/s、雷诺数Re= 5×105、升沉幅值h0=c、俯仰幅值θ0= 75°、升沉运动与俯仰运动之间相位角φ= 90°的参数工况下，结合扑翼的力与力矩系数、功率系数曲线的周期性变化，以及扑翼周围涡量场和压力分布，探讨了不同尾缘襟翼偏转形式对扑翼获能特性的影响规律。同时本文还对比了尾缘襟翼与格尼襟翼两种不同襟翼控制方式对扑翼获能性能的影响。得到结论如下：

1）尾缘襟翼向压力面偏转的控制策略的获能效果明显优于向吸力面偏转的情况，其中向吸力面偏转导致了扑翼的获能效率随缩减频率增大而快速降低，在高缩减频率下则出现了负效率的情况，获能效率大幅下降。

2）从升沉力和俯仰力矩两个方面综合来看，因为扑翼获能过程中升沉力做功占比更大，因此尾缘襟翼向压力面偏转更有利于提升扑翼获能效率，其中连续偏转的TP 式控制策略最优。

3）格尼襟翼对扑翼的获能效率提升效果主要体现在中低缩减频率工况（f* = 0.08～0.14），在f* =0.12 时，与原始扑翼相比，获能效率最大可提高到41.2%。随着缩减频率进一步增大，获能效率逐渐与原始扑翼趋近。而尾缘襟翼对扑翼的获能效率提升效果主要体现在中高缩减频率工况（f* = 0.12～0.22），在f* = 0.18 时，与原始扑翼相比，获能效率最大可提高到46.3%。

因此，在工程实际中需要根据设计工况下扑翼的运动频率，采用合适的控制方法最大程度地提高这种装置的风能、水流能捕获能力。