基于PSP/TSP 测量的TSTO 标模级间分离气动干扰特性试验分析

解福田，张庆虎，林敬周，*，彭 迪，陈 磊

(1. 中国空气动力研究与发展中心 超高速空气动力研究所，绵阳 621000；2. 上海交通大学 机械与动力工程学院，上海 200240)

0 引 言

因关系到飞行成败，飞行器多体分离时的气动干扰问题一直是研究热点[1-2]。不断有学者通过数值模拟和风洞试验[1]研究多体分离问题，如导弹助推子级分离[2-3]、保护罩分离[4]、机弹分离 [5-7]等。但对于体积和质量相当的两级入轨空天飞行器（two-stage-toorbit, TSTO），其并联级间分离问题的研究还比较少。近年来，TSTO 因具有较高的经济性和可实现性而获得了科学家们更广泛的关注[8-10]。TSTO 并联飞行器的助推级一般具有大升力面，分离时气动干扰对飞行器气动力/力矩的影响较大，气动干扰也更加复杂，特别是高马赫数高动压下，分离使气动干扰问题更加突出。高超声速TSTO 并联分离往往发生在中低空大动压条件下，级间存在着复杂的强激波干扰[11]，两级头部激波常常能直接作用到彼此表面，形成同时包含多个激波反射、激波与激波干扰、激波与边界层干扰等[12-14]的复杂三维波系结构，改变级间压力和温度分布，进而改变飞行器的压心、力和力矩，显著影响飞行器的稳定性、分离安全性和热载荷分布等。获得分离气动干扰特性、探索影响分离特性的主要因素和气动干扰规律对TSTO 分离安全性评估具有重要意义。

国外较早开展了并联两级分离气动特性和流动机理的研究，并取得了一定进展。Moelyadi 等开展了马赫数4 到马赫数7 定常和非定常情况下两级分离气动特性机理研究[15-16]，模拟结果展示了两级之间产生的入射激波、反射激波和膨胀波所带来的强烈的气动干扰问题，特别是在初始分离时刻，激波带来的气动干扰给升力和俯仰力矩的预测精度带来了较大影响。Chaplin 等[17]研究了Ma= 3 时细长体之间的干扰，研究发现由激波入射引起的法向力和俯仰力矩最大改变分别发生在等效入射角为−2.7°和6°时。Laurence 等[18]研究了高超声速下圆柱和球体之间的干扰特性，发现二级下游的干扰诱导产生了较大升阻力，且当二级下游位于主体弓形激波内时干扰现象最严重，这一情况的主要影响因素是入射激波与边界层的相互作用（shock wave boundary layer interactions, SBLI）。早期研究表明SBLI 会在激波入射区域产生局部高压和强烈的加热现象，这是高速飞行器中最受关注的气动问题[19-20]。非定常压力载荷是SBLI 影响飞行器性能和安全的另一个关键问题[21]。国内王元靖等[22]开展了并联圆柱体外形分离过程中的气动干扰试验，研究发现，当再入体处在助推器头部激波区域内，再入体受到的气动干扰较小，而当再入体穿越过助推器头部激波时，受到的气动干扰急剧增大。林敬周等[23]建立了高超声速双体轨迹捕获试验技术，从气动力和运动轨迹两个方面分析了两级分离特性。王粤等[24]采用数值方法研究了简化并联二维楔形体分离流场结构与轨道级抬升角的关系。

上述研究对象多为锥柱体外形或者二维楔形体，与真实大升力体外形存在差异。同时，关注的物理量主要是气动力、分离轨迹、姿态角[25-26]，缺少壁面压力、温度等。激波/边界层干扰及其他因素导致的局部热流峰值和压力脉动现象等，对飞行器外形、热防护、控制系统与动力系统设计具有十分重要的影响[11]。为获得级间激波/边界层干扰下的高分辨率大面积连续压力和温度分布规律，需要开展级间壁面压力、温度等物理量的精细化测量试验。

本文基于压敏漆（pressure sensitive paint, PSP）/温敏漆（temperature sensitive paint, TSP）测量技术开展了TSTO 并联分离级间模型表面压力和温度特性的研究[27]。以某TSTO 并联两级入轨飞行器标模[28]为研究对象，该标模级间壁面是被测量表面。Φ0.5 m高超声速风洞PSP/TSP 光路位于试验段和试验模型上方，所研究的TSTO 模型轨道级对两级测量表面均形成大面积遮挡，光路无法穿透轨道级模型到达级间被测量区域。针对上述问题，本文提出了一种可以在有遮挡条件下实现并联两级模型级间表面压力、温度同步测量的PSP/TSP 测量方法，获得了级间干扰气动特性。

1 试验模型与关键测试方法

1.1 试验模型

本项试验在中国空气动力研究与发展中心的FD-30B（Φ0.5 m）常规高超声速风洞中开展。试验模型如图1 所示。由于更关注级间区域模型表面的压力/温度分布，为降低风洞堵塞度，在原始外形[28]（图1（a））基础上，本文对模型级间区域表面之外的助推级（一级）进行了缩减调整。在不影响测量结果的情况下尽量减小一级模型宽度。考虑超出部分对级间测量面的压力/温度分布影响较小，模型两侧保留头部大后掠角侧缘，切除沿侧缘线向后延伸超出的部分。不考虑两级模型垂尾和舵偏的影响。

图1 TSTO 试验模型调整过程Fig. 1 Simplification of the TSTO test model

一级模型原上表面为平直表面，下表面为弧形曲面。为了降低一级模型下表面弧形曲面的玻璃窗口加工难度和光路畸变，将一级模型下表面调整为平直表面。同时，对轨道级模型做适当修整，去掉了背部垂尾和体襟翼。调整后模型如图1（b）所示。本文简化处理的部件远离测量表面（级间区域），已在前期工作中对简化外形开展了数值计算，流线、压力分布和激波结构分析的结果均表明简化部分的流动改变不会对级间区域产生实质影响。

1.2 有遮挡条件下的测试方法

由于轨道级模型位于助推级模型之上，想要获取级间流动特性，采用PSP/TSP 光源直接照射模型表面、图像采集系统捕获压力/温度信息的传统方法已不再适用。为解决有遮挡条件下的压力/温度测量难题，本文提出以金属模型为主体、一级模型局部开设上下表面两层石英光学玻璃窗口的方法。综合考虑透光率、加热影响及气流杂质冲击等因素，经仿真验证，两层光学玻璃厚度均设计为5 mm；为降低风洞气流冲击和模型震动的影响，光学玻璃与金属模型之间设置0.2～0.5 mm 厚的缓冲涂层。

模型装置设计为反装方式，以便充分利用一级模型具有较大水平投影面积、更利于开设石英玻璃窗口的优势（图2）。为降低支撑干扰[29]，两级模型均采用尾支撑方式，且一级尾支撑设计成“H”形，以减少对光路的遮挡。为提高法向级间距的调节精度，设计了连续调节装置，在支撑装置上设计了多个可相对滑动的卡槽螺杆和可在任意位置停留的锁紧装置。

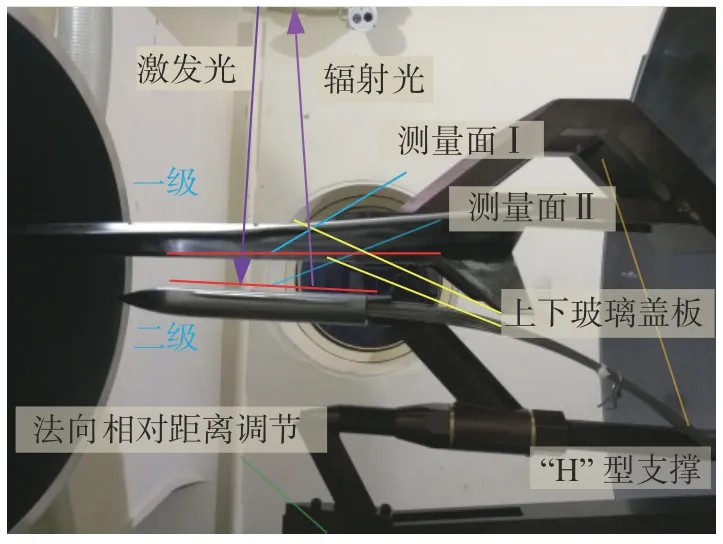
图2 试验模型级间距连续调节装置Fig. 2 Device for continuous adjustment of the stage spacing of the test model

如图3（a）所示，二级模型测量面Ⅱ在进行压力和温度测量时，对称喷涂PSP/TSP 涂层；采用周围点双线性插值法恢复中线的压力和温度数据；模型表面布设测压孔，以获得扫描阀压力数据，用于原位校准（on-site calibration[30]），提高PSP 数据精准度；测压孔处PSP 数据采用高斯滤波法修复。TSP 测量工作获得温度分布数据的同时，也可利用这些数据对PSP 数据的温度效应进行修正。一级模型上下表面光学玻璃（图3（b））均不作处理，仅用于光路透过。

图3 PSP/TSP 喷涂效果及测量装置Fig. 3 PSP/TSP spraying effect and the measurement device

如图3（c）所示，一级模型测量面Ⅰ在进行压力和温度测量时，模型上表面光学玻璃用于透光，下表面光学玻璃则对称喷涂PSP/TSP 涂层。为避免二级模型发光分子信号的干扰，测量面Ⅱ的涂层全部清除，并喷涂黑色哑光漆，以减小模型表面散射光的影响。由于一级模型光学玻璃表面不宜开设测压孔，所以用于PSP 原位校准的扫描阀压力数据来自于单独设计的金属盖板的测压数据。PSP 和TSP 涂料对称分布在一级模型表面。

试验时，光源和相机以几乎垂直的视角安装于模型上方，以获得最大分辨率。光源和相机固定在试验段外的支撑装置上，不与试验段接触，以避免试验段部件振动对其带来的干扰。光源和相机共用试验段上方开设了直径Φ200 mm 的观察窗口。窗口距模型约1250 mm，相机上加滤光片并调整拍摄角度以消除玻璃窗口反射对相机造成的二次干扰。二级和一级模型的光路分别如图4 和图5 所示。图6 给出了PSP/TSP 发光分子被激发后的模型照片。

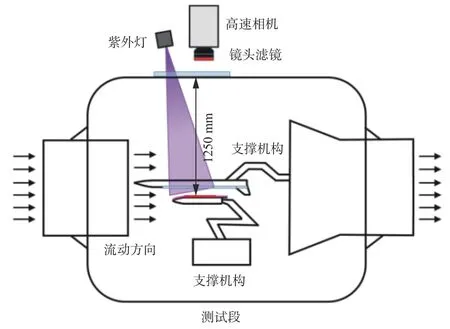
图4 二级模型测量装置示意图Fig. 4 Schematic diagram of the measurement system of the second-stage model

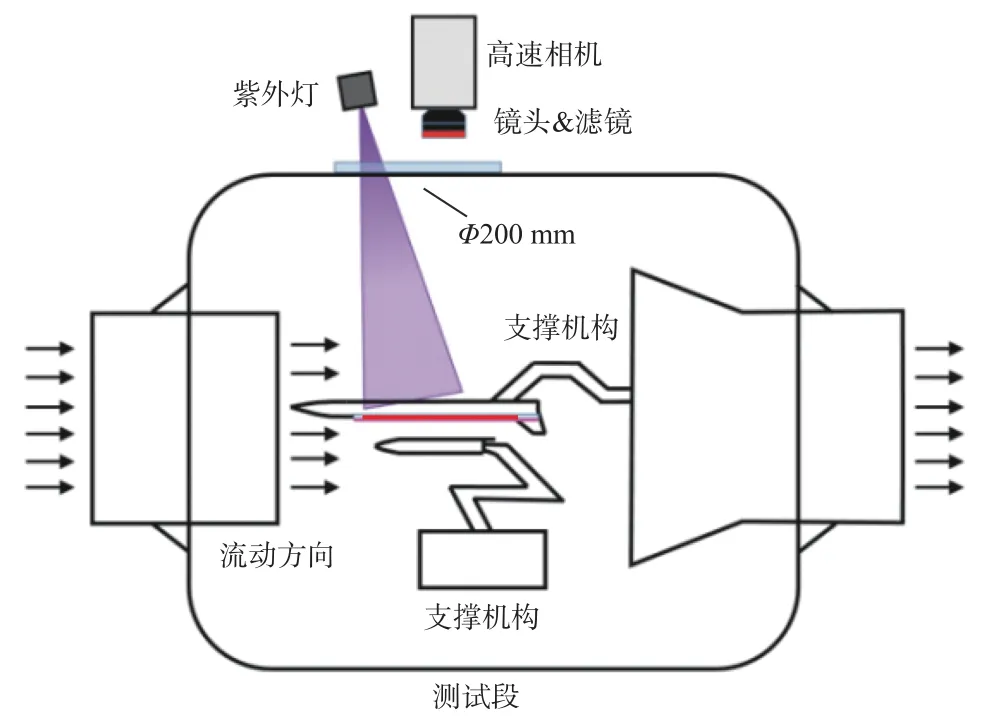
图5 一级模型测量装置示意图Fig. 5 Schematic diagram of the measurement system of the first-stage model

图6 试验段内二级模型PSP/TSP 涂料激发照片Fig. 6 Snapshot of the second-stage model illuminated with PSP/TSP under test

2 试验工况

风洞来流马赫数Ma∞=6，总温T0=497 K，动压q∞=30 kPa，对应飞行高度H∞=30 km。试验模型状态参数见表1。

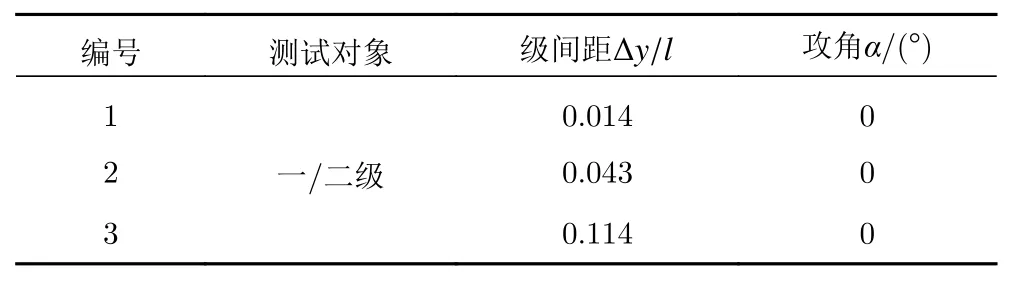
表1 试验模型状态Table 1 States of the test model

模型级间距Δy/L定义为两级相对初始位模型法向位移Δy与参考长度L之比，如图7 所示，其中参考长度L为二级模型长度,d0为初始相对距离，d0=1.875 mm。

为降低温度效应影响，根据TSP 测量结果对模型不同工况下的PSP 测量结果进行温度修正，再结合测压孔数据进行在线标定。由于不同车次的来流静压不同，为便于比较，压力数据以无量纲压力系数Cp给出：

其中，p∞为来流静压，p为测点压力。

3 并联级间分离气动干扰特性

3.1 级间激波系结构

图8 给出了不同级间距下的风洞试验纹影截图及数值模拟获得的密度云图，可以看出两者显示的流场波系结构基本一致。从图8（a）可以看到，级间距Δy/L= 0.014 时，级间流场呈现出典型的缝隙流动，除了二级头部激波入射至一级上壁面，激波/边界层干扰引起的流动分离所产生的分离激波及第一道反射激波外，级间没有出现明显的波系结构。从图8（b）可以看到，级间距Δy/L= 0.043 时，随着级间距增大，级间波系结构变得复杂，激波在级间多次反射，并在上下壁面引起流动分离，形成了典型的小通道流动。随着级间距的进一步增大，Δy/L= 0.114 时，级间激波反射距离增加，反射次数明显减少，仅出现两次反射。此外，图8（c）中清晰可见第一次反射激波入射至二级下壁面，引起边界层流动分离所产生的分离激波。

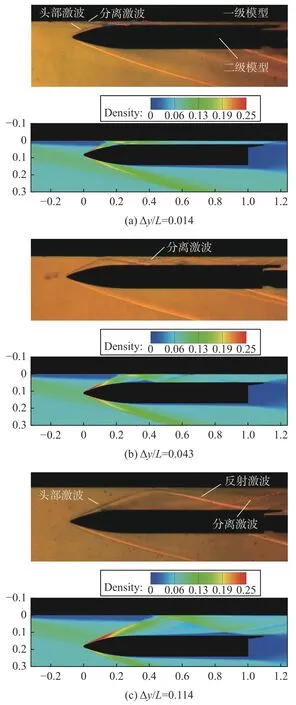
图8 攻角α1,2=0°时不同级间距下纹影截图Fig. 8 Schlieren snapshots of the model with different state spacing under the angle of attack α1,2 = 0°

为了弄清楚Δy/L= 0.014 时的级间激波结构，结合两级模型中线压力分布曲线和壁面压力分布云图进行分析。如图9 所示，子图（a）为一级模型Cp~x/L曲线，子图（e）为二级模型Cp~x/L曲线。保持曲线图和压力云图的x/L坐标值一致，均缩放调整至0～1 范围内，并对齐。从纹影图中可知，在小级间距时，二级头部激波SW1（示意图中红色虚线）与边界层干扰，一级模型壁面产生了一个清晰可见的分离激波DW1（示意图中的蓝色虚线）。结合压力分布不难推出：分离激波入射到二级下壁面DE1 处形成二级模型的第一个压力峰值，反射后在一级模型上壁面DE2 处形成一级模型的第二个压力峰值，再次反射后在二级模型下壁面DE3 处形成二级模型的第四个峰值。纹影图中显示，二级模型头部激波SW1 入射至一级模型上壁面SE1 处并反射，从一级模型Cp曲线可知，在反射点SE1 处形成了一级模型的第一个压力峰值。SW1 在SE1 反射后入射至二级模型壁面SE2 处，从二级模型Cp曲线可以看出，在SE2 处形成了二级模型的第二个峰值；SW1 从SE2 反射达到一级模型壁面，在SE3 处形成一级模型的第三个峰值。而二级模型第三个峰值点无法对应到SW1 和DW1，推测认为，在一级模型壁面DE2 点之前存在一道分离激波DW2（绿色实线），DW2 入射至二级模型壁面后形成了二级模型Cp曲线上的第三个峰值。由此可见，在Δy/L= 0.014 的极小级间距下，头部激波干扰较强，容易诱导流动分离，分离激波与头部激波同时在级间不断反射，共同改变了模型壁面压力。级间两条主激波的反射激波系结构解释了级间壁面密集的压力突变，该压力突变并非二级头部激波单一反射干扰形成的。

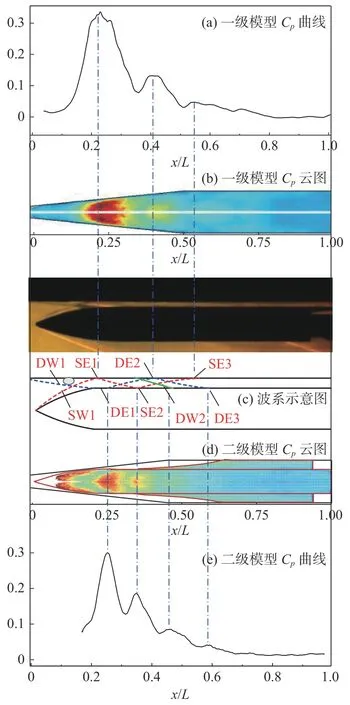
图9 攻角α1,2=0°时Δy/L = 0.014 级间距下激波结构Fig. 9 Shock structure for the model with stage spacing Δy/L = 0.014 under the angle of attack α1,2 = 0°

3.2 级间壁面压力分布特征

图10 给出了基于PSP 测量技术获得的上下模型表面压力云图、中心压力曲线和级间激波结构示意图。从不同级间距的波系结构看，随着分离距离的变化，波系结构会产生较快的位置改变，级间距越小，头部激波干扰位置越靠前且强度越高，同时级间激波反射次数和压力突变点也越多。由压力云图可见，3 种级间距下，激波入射后，级间上下壁面的压力明显升高；相应模型中心线上的压力分布也出现多个峰值，且峰值出现位置与激波入射位置相对应；随着激波在级间不断反射，激波强度逐渐减弱，压力峰值也不断下降。

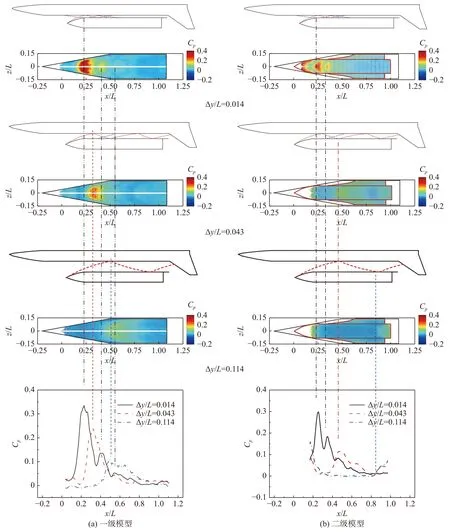
图10 攻角α1,2=0°时不同级间距下模型表面压力系数分布Fig. 10 Pressure distribution on the model with different stage spacing under the angle of attack α1,2=0°

对于Δy/L= 0.014 的缝隙流，两级压力峰值主要出现在级间前段（x/L≤0.45），中后段未见明显压力峰值，这与图8（a）除前段外，级间未见明显波系结构的流场特征吻合。由激波入射处壁面压力会明显抬升形成压力峰值可以判断，来自二级模型头部激波的一级模型上壁面第一道激波，其入射位置位于x/L=0.22 附近；来自二级模型壁面反射的第二道激波，其入射位置位于x/L= 0.42 附近。而二级模型下壁面引起第一个压力峰值的入射激波来自于一级模型表面激波/边界层干扰形成的分离激波，其位置位于x/L=0.26 处；位于x/L= 0.34 附近的第二个压力峰值则由一级模型壁面的反射激波引起。从Cp~x/L曲线可以看出，激波经反射后强度衰减较快，一级模型第一个压力系数峰值为0.34，第二个压力系数峰值则下降至0.13；相应地，二级模型的两个压力系数峰值分别为0.29 和0.18。

对于Δy/L= 0.043 的小通道流，整个级间区域出现多次激波反射；随着反射次数增多，激波强度逐渐减弱，压力跃升减小。一级模型激波反射点位置分别位于x/L= 0.28、0.75、1.1 附近，二级模型激波反射点位置分别位于x/L= 0.42、0.8 附近。

对于Δy/L= 0.114，由于接近大通道流，可以看出相较于小通道流动，激波反射点间距加长，反射点位置后移，致使级间反射明显减少，反射点仅出现在一级模型上壁面x/L= 0.5 和二级模型下壁面x/L= 0.84附近。

总的来说，级间存在多次激波反射时，第一次激波入射区域的干扰最为强烈，随着级间距增大，压力峰值降低且峰值位置明显后移。这表明级间距越小，干扰越靠前，级间激波/边界层干扰对飞行器两级气动特性的影响越大。

由以上分析可知，受头部激波和头部激波的反射激波干扰影响，两级模型中线上的压力呈现有多个峰值的特点。随着级间距增大，激波强度减弱，干扰后压力峰值减小。随着x/L距离增大，激波反射次数增加，反射激波干扰明显减弱，激波干扰后能量降低、强度减弱，压力峰值也相应下降。级间距增大和x/L距离增大均能导致压力峰值减小，但两者原因不同。由于无法预知哪种情况导致的压力峰值衰减更快，为找到压力峰值衰减的规律，本文汇总了一级、二级模型在三个级间距下的中线处的全部压力峰值位置数据。由于本试验观测的级间距只有3 种，数量较少，所以选择了x/L作为主要变量，得到了压力系数峰值Cp_max和横向坐标x/L之间的关系，如图11所示。由此图可以发现，压力峰值大小与峰值横向位置高度相关，随着峰值位置后移，峰值呈现指数规律下降，上下两级模型压力峰值均在同一条曲线上。该曲线反映了激波干扰强度随干扰距离、激波反射次数的综合衰减速度。整体上，随干扰位置后移，激波强度减弱，干扰强度、衰减速度也相应减小。

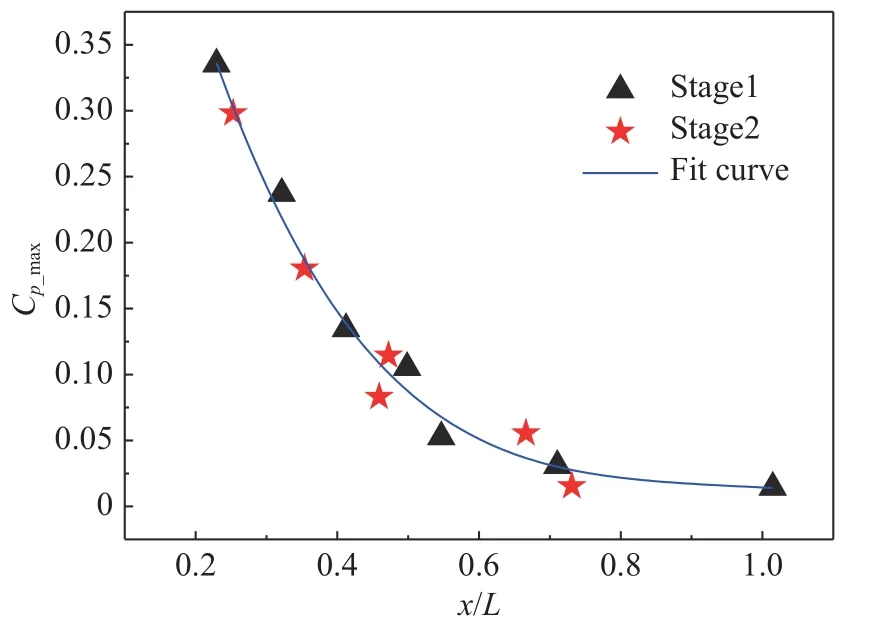
图11 不同级间距下模型表面压力系数峰值分布Fig. 11 Peak pressure distributions on the model with different stage spacing

3.3 级间表面温度分布特征

TSP 涂料的耐冲刷特性良好，在气流的冲刷下温度分布细节保持得更加完整。

图12 给出了基于TSP 技术获得的模型表面第1 秒时刻的温度分布，可以看出，在二级模型头部激波入射前，一级模型上表面的无干扰区域最高温度约55 ℃，干扰后区域的最高温度约83 ℃。可见，入射激波使得气流急剧压缩，导致模型表面温度显著升高。对比两级模型表面的整体温度分布可知，二级模型表面最高温度约62 ℃，明显低于一级模型表面最高温度。这除了因为反射激波强度逐渐减弱外，还因为二级模型表面金属材料热导率高于一级模型表面石英玻璃热导率。

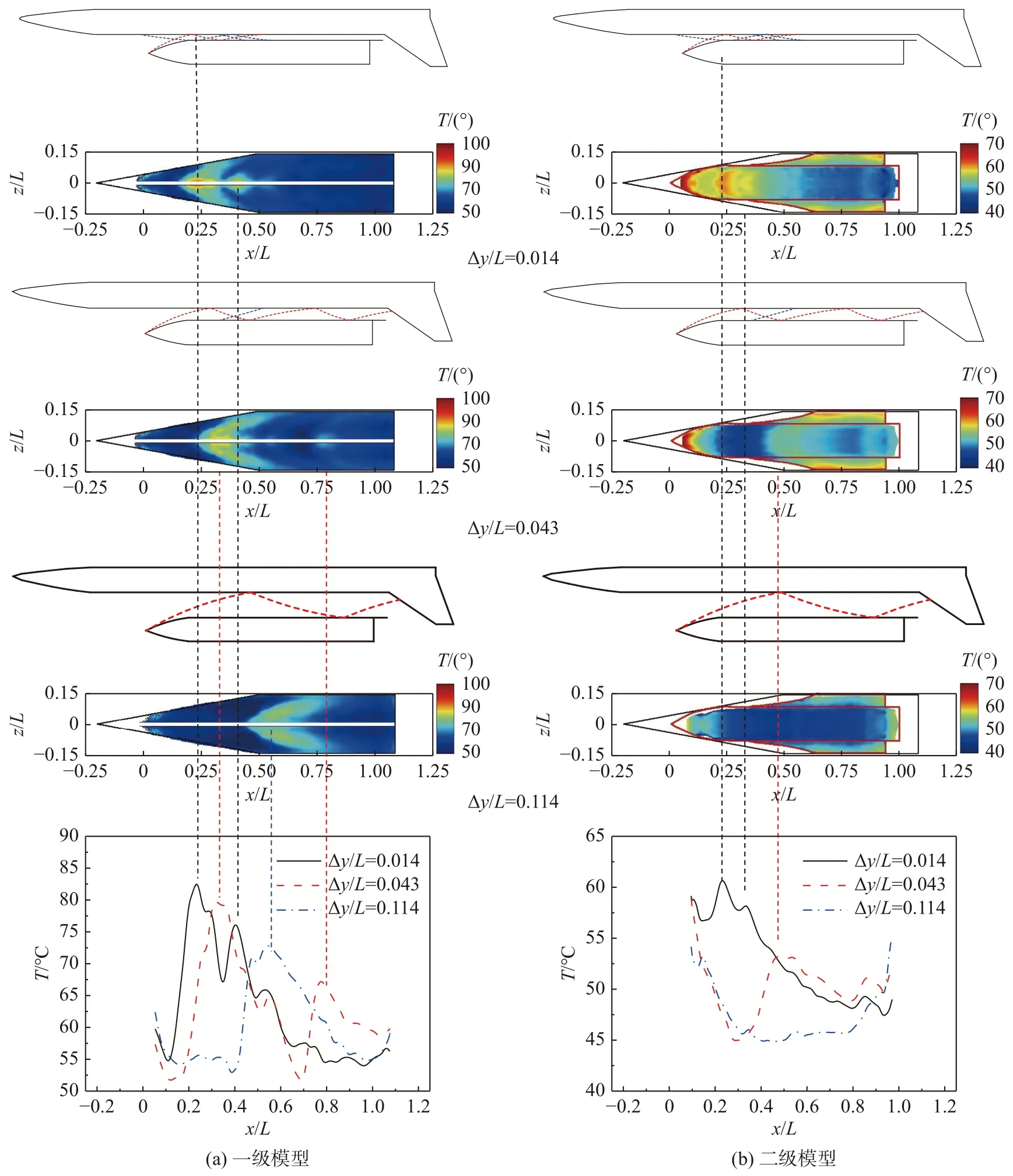
图12 攻角α1,2=0°时不同级间距下模型表面温度分布Fig. 12 Temperature distributions on the model with different stage spacing under the angle of attack α1,2=0

由图12 中沿模型中心线的温度分布曲线可以看出：

对于Δy/L= 0.014 的缝隙流，在x/L≤0.45 范围内，一级模型表面出现两个递减的显著温度峰值，其值分别为83 ℃和75 ℃；而中后段温度分布则逐渐趋于激波干扰前的温度分布。二级模型表面的两个温度峰值分别为62 ℃和56 ℃，这与图10 的压力分布特征相匹配—激波入射之处压力和温度均明显升高。

对于Δy/L= 0.043 的小通道流，激波在级间区域来回反射，所到之处均有引起壁面温度跃升；但随着反射次数的增加，激波强度减弱，温度峰值降低。

对于Δy/L= 0.114，由于接近大通道流，可以看出相较于小通道流动，此时的激波反射次数明显减少，随着级间距的增大，温度峰值显著减小。

图13 给出了采集图像过程中第1 秒到第3 秒时刻的模型表面温升分布。可以看出，模型表面激波区域温升明显高于其他区域。此外，由于模型材质的导热性能有所差异，一级模型的整体温升稍大。从模型中心线附近的温升分布可以看出，一级模型中段受反射激波的影响，温升先升高后降低；二级模型头部激波的波后温升先降低，在中部保持较低水平，在尾部反射激波区域再上升。随着级间距增大，入射至模型表面的激波强度减弱，激波区域的温升峰值也逐渐降低。

无论温度值还是温升分布都与压力分布规律相似，不同的是温度曲线峰值附近温度变化较平缓，这显示了受模型传热的影响，温度变化没有压力变化剧烈。温升主要由激波干扰引起，其分布与流场激波结构一致。此外，不同级间距下温度峰值，特别是温升的峰值，差异较小。二级模型的温度分布受到模型材质影响，与激波结构差异较大。

从图14 中可以看出，随着激波干扰位置后移，不同峰值位置的温度近似呈线性下降关系，这表明激波干扰强度逐渐减弱。与压力分布不同，温度下降趋势比较平缓，且两个模型的温度峰值不在同一条曲线上。这主要是因为二级模型为金属材质，干扰点热量快速向低温区传递，导致温度峰值低于一级模型。

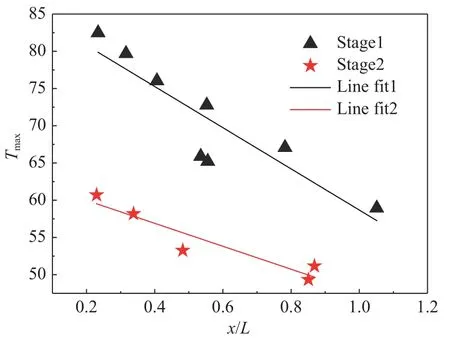
图14 不同级间距下模型表面峰值温度分布Fig. 14 Peak temperature distribution on the model with different stage spacing

综上，二级模型头部激波在两级模型间来回反射，产生复杂的波系结构和流场结构，形成多个压力峰值和温度峰值，随着反射次数的增加，激波强度衰减，峰值减小；随着级间距增大，二级模型头部激波入射位置后移，入射激波前的压力和温升恢复至激波干扰前的特征。

4 结 论

本文基于PSP/TSP 测量技术开展了并联TSTO标模级间干扰特性试验研究，获得了级间干扰区域的压力和温度分布特性。研究结果表明：

1）头部激波干扰产生的级间流动结构呈现从缝隙流到小通道流再到大通道流的流动特征。处于小通道流时，头部激波入射至壁面后，在两级之间多次反射，形成复杂“激波串”结构。随着级间距增大，激波反射次数减少，反射点位置后移，直至脱离模型。

2）级间壁面中心线压力在反射点附近形成多个压力峰值，其中第一道入射激波最强，干扰产生的压力峰值也最大；随着激波反射次数增加，其强度不断减弱，压力峰值也逐渐降低。从平面分布特征看，头部激波和侧缘激波在壁面形成了弧形压力干扰区，中心点压力最高，两侧压力逐渐降低。级间距越小，激波干扰越剧烈，最大压力峰值位置也越靠前；级间距改变了压力抬升位置和峰值，进而改变了不同级间距下的气动力干扰量。

3）激波/边界层干扰显著增加了模型级间壁面局部温度。随着级间距的增大，激波/边界层干扰几乎影响了整个级间区域，但温度峰值是逐渐降低的。

本文当前给出的压力分布特性主要基于PSP测量的时均结果，更多展示的是级间干扰流场的定常压力分布特性，后续将针对级间干扰流场的非定常效应开展进一步研究。

致谢：感谢中国航天空气动力技术研究院沈清、陈兰、胡静等在TSTO 标模多体分离特性研究中的支持，感谢中国空气动力研究与发展中心超高速所范孝华为本次研究提供数值模拟支持。