高超声速风洞双体同步分离捕获轨迹试验技术

林敬周，解福田，钟 俊，邹东阳，*，皮阳军

(1. 中国空气动力研究与发展中心 超高速空气动力研究所，绵阳 621000；2. 重庆大学 机械传动国家重点实验室，重庆 400044)

0 引 言

高超声速飞行器多体分离过程中，由于高速大动压下复杂流场带来的强耦合、强干扰特点，涉及流动分离、激波/边界层干扰、激波/激波干扰、激波/膨胀波干扰、激波/旋涡干扰等现象，流动呈现高度的非定常、非线性特征，能否安全分离成为关键难题[1-7]。开展多体分离研究对于高超声速飞行器研制发展具有重要意义，风洞试验相较飞行试验在周期、成本、风险等方面具有突出的优势，是开展多体分离安全预测的重要地面手段之一[8-10]。

为了研究多体分离问题，美国AEDC 于20 世纪70 年代在VKF-A（马赫数为1.5～5.5）、VKF-B（马赫数为6、8）、VKF-C（马赫数为10、12）风洞中建立了一套共用的捕获轨迹系统（captive trajectory system,CTS），可进行一体固定、一体运动的飞行器平行分离、轴向串联分离、外挂物分离等试验[11-12]，试验模式主要分为网格测力和捕获轨迹两种类型。从公开报道的文献来看，网格测力模式在3 座风洞中均有应用，而捕获轨迹模式主要应用于马赫数4 以下的分离试验。如以串联分离形式为代表的Ares 运载火箭和Hyper-X 计划曾分别在VKF-A 风洞马赫数为4.5～5.5、VKF-B 风洞马赫数为6 的条件下开展了大量的级间分离网格测力试验，建立了分离干扰试验数据库，并基于该数据库开展了离线轨迹计算[13-14]。以并联分离形式为代表的BETA TSTO（two-stage-to-orbit,TSTO）两级入轨空天飞行器在VKF-B 风洞马赫数为8 的条件下开展了大批量的并联分离网格测力试验，并根据获得的数据进行了离线轨迹预测[15]。除美国之外，法国ONERA 于20 世纪70 年代具备了马赫数为3 以下的单体CTS 试验能力，并在Modane-Avrieux Centre 的 S2MA 风洞中开展了相关试验研究[16]。加拿大国家研究院的航空航天研究所在Ma=3 下吹式风洞中配套了CTS 机构，于20 世纪90 年代中期开展了外挂物分离的轨迹模拟研究，最大试验马赫数为1.4[17]。2001 年，德国慕尼黑工业大学针对TSTO 的级间分离问题开展了联合研究，试验在俄罗斯ITAM 的T-313 风洞中进行，试验类型为网格测力，来流马赫数为4.04[18]。2012 年，日本针对TSTO 也开展了多体分离试验研究，但主要还是以网格测力技术为主[19]。总的来说，迄今为止国外在亚跨超声速范围内具备的CTS 试验技术均为一体固定、一体运动的单体捕获轨迹技术，在高超声速范围内开展的多体分离试验研究仍以网格测力为主，未见单体捕获轨迹试验技术的报道，也更未见双体均能进行捕获轨迹试验技术的报道。

国内，以中国空气动力研究与发展中心、中国航天空气动力技术研究院、中航工业气动研究院为代表的气动专业研究机构，航空航天工业部门以及部分高等院校，都针对多体分离问题开展了长期的研究工作。中国空气动力研究与发展中心高速空气动力研究所于20 世纪80 年代率先在国内建立了第一代跨超声速风洞CTS 试验技术，针对载机投放/发射及具有舵面控制的外挂物分离模拟方面开展了大量试验研究，并于2011 年成功将CTS 技术应用于超声速风洞[20-22]。至2016 年，高超声速多体分离试验研究主要以网格测力试验技术为主，如马赫数为7 的子母弹在子弹抛撒时的分离干扰研究、飞行器并联式多体系统分离过程中的气动力干扰试验研究、马赫数为5～8 的导弹/运载火箭级间分离气动特性研究等[23-28]。2017 年，中国空气动力研究与发展中心超高速空气动力研究所在国内首次形成了高超声速风洞单体CTS 试验技术能力[29]。

近年来，随着高超声速飞行器的飞速发展，飞行器外形愈加复杂，面临的问题也日益突出。当质量与体积相当的两体进行分离时，分离过程中的复杂流动干扰严重影响飞行器气动特性的同时，也使两体飞行姿态均产生显著变化。一体固定，另一体进行捕获轨迹的单体CTS 试验技术已不能满足模拟需求。为此，本文提出了高超声速风洞双体同步捕获轨迹试验模拟方法，在中国空气动力研究与发展中心超高速空气动力研究所建立了双体同步捕获轨迹试验技术，并在FD-30Φ1m 高超声速风洞开展了马赫数为6 的验证试验。

1 主要技术难点与解决措施

本文建立的高超声速风洞双体同步捕获轨迹试验技术基于Φ1 m 高超声速风洞单体CTS 试验系统（上CTS 系统）及下攻角机构系统（图1）进行研发。首先对已有的下五自由度（轴向x、法向y、俯仰θ、偏航ψ和滚转φ）模型攻角机构系统进行改进研制（改进后称下CTS 系统），使其在保留原有控制及运动功能的同时具备CTS 功能，用于支撑双CTS 试验的主体模型，使主体模型能准确、快速和平稳地到达解算出的捕获轨迹点位置，模拟分离时的主体运动轨迹。同时它可与现有上六自由度（轴向x、法向y、侧向z、俯仰α、偏航β和滚转γ）CTS 系统实时通信联动，共同实现双体同步捕获轨迹。相较单CTS 试验技术[29]，双CTS 试验技术的难点主要为双CTS 系统联动组合控制系统研制、双CTS 捕获轨迹运动分配及双体同步捕获轨迹控制策略。

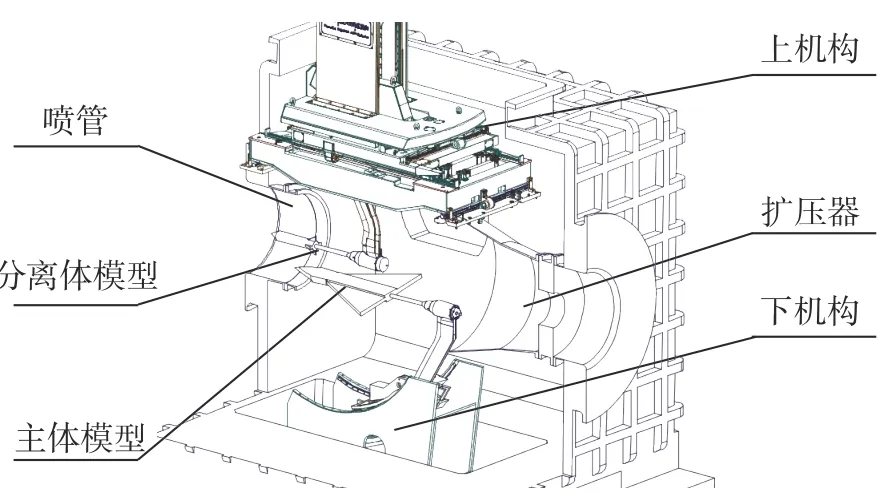
图1 双CTS 机构示意图Fig. 1 Schematic of the dual CTS mechanism

1.1 双CTS 机构联动组合控制系统研制

在高超声速双CTS 试验中，控制系统用以控制上/下CTS 机构的同步运动，从而使两体模型在各自所在CTS 机构的带动下实现分离轨迹的模拟，运动包括上6 个自由度：轴向x、法向y、侧向z、俯仰θ、偏航ψ和滚转φ，下5 个自由度：轴向x、法向y、俯仰θ、偏航ψ和滚转φ。

针对高超声速风洞流场和电磁场较为复杂、双CTS 机构的自由度个数较多（11 个）、两级轨迹模拟实时性和同步性要求较高等难点，提出了“数采（天平、总压等）、解算（气动/动力学）、上/下机构联动组合控制、上/下机构运动分配”四位一体的设计方式。

硬件上采用基于PC 的运动控制技术和高速实时以太网总线EtherCAT 技术相结合的方式构建了整个控制系统。现场总线控制模式使系统布置更为灵活，且提高了控制系统的抗干扰性，图2 给出了控制系统拓扑图。其中，为了增强系统抗干扰能力，将用于采集与传输伺服控制中数字/模拟量信号的I/O 模块分成了主站和从站两个部分。主站的I/O 模块主要用于布设在机构上的振动加速度传感器和磁栅尺信号的采集与传输，从站的I/O 模块主要用于风洞前室总温总压和模型天平测力信号的采集与传输。

图2 控制系统拓扑图Fig. 2 Topology diagram of the control system

利用TwinCAT3.0 开发平台编写数据采集、气动及动力学解算、运动控制、运动分配的软件系统，实现了“四位一体”的系统设计。基于快速实时运动轨迹规划及插补算法，结合具有高动态响应特性的电机驱动伺服系统，有效地保证了双CTS 机构的控制性能。

1.2 双CTS 捕获轨迹运动分配方法研究

在实际的双CTS 试验中，如果不对双CTS 系统进行运动分配，则会存在主体和分离体模型同向运动而浪费机构行程的问题，降低试验效率。并且下CTS 机构无z向自由度，不进行运动分配，这也会导致双CTS 试验的适应性弱，无法实现双体各自6 个自由度、共12 个自由度的轨迹模拟。

为解决以上问题，提出了一种基于关节驱动运动极限的双CTS 系统运动分配方法。由于双CTS 试验对姿态角进行运动分配会导致两级之间的分离流场失真，因此运动分配只针对线位移，即平动进行分配。本方法综合考虑了机构各个自由度驱动的运动极限，并认为下攻角机构无自由度仅是驱动关节运动量极限为0 的特殊情况。该分配方法最大化地利用了各个驱动的运动极限，弥补了下CTS 机构无z向自由度的缺点；且保证了运动分配之后主体和分离体模型之间的相对位姿关系较分配之前不变，以及两个模型相对于来流方向的姿态较分配之前不变。

假设分配前的目标运动量：上机构为a，下机构为b，上下机构目标运动量之差c=a−b。根据上下机构的剩余行程进行加权分配，假设上机构的余下行程为Lu，下机构的余下行程为Ll。分配之后，上机构运行的实际运动为a0，下机构的实际运动为b0。将下机构的z向自由度的余下行程设置为0，则可将上下机构的z向相对运动全部分配至上机构而保证上下机构的相对位置不变（图3）。

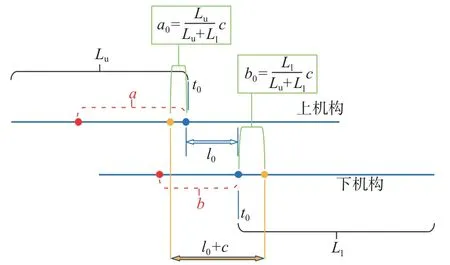
图3 上下机构运动分配原理Fig. 3 Principle diagram of the motion distribution between the upper and lower mechanisms

通过该种运动分配方法，实现了真实飞行器双体各自6 个自由度、共12 个自由度的分离轨迹全模拟。

1.3 双体高精度同步捕获轨迹控制策略

对于高超声速风洞多体分离试验而言，由于风洞运行时间短（≤60 s），通常需要在50 s 左右完成双体轨迹的模拟，因此要求在保证精度和准度的前提下快速实现捕获轨迹，并确保双体分离高精度同步，从而实现双体之间位姿关系的准确模拟。为此，提出了基于位置控制和连续轨迹控制模式的两种高精度同步捕获轨迹控制策略，同步精度优于4 ms。

图4 给出了双体同步捕获轨迹位置控制策略：在初始位置时（此时上、下CTS 机构均处于静止状态），上、下机构同时进行数据采集，同时气动解算下一个轨迹点的位姿，并生成当前点到下个轨迹点的轨迹，然后进行上、下机构运动分配。按照运动分配结果重新规划轨迹，上、下机构分别驱动各自装载模型按各自规划轨迹运动，到达目标点位后机构停止运动（停留时间≥0.5 s）。确认上、下机构均已到达目标点、停止运动后，开始新的一个轨迹周期的数据采集、气动解算、轨迹生成、运动分配、轨迹重新规划、模型运动、到达下一个目标点位。如此循环，直至试验结束，完成双体同步分离两条轨迹的捕获。

图5 给出了连续轨迹控制策略：与位置控制策略相同的是，在初始位置时上、下CTS 机构均处于静止状态，上、下机构同时进行数据采集、气动解算、轨迹生成、运动分配、轨迹重新规划、机构驱动模型运动；不同的是，到达下个轨迹点后机构并不停止运动而是始终处于连续运动状态。在运动到下个轨迹点之前的某一时刻即提前进行数据采集、气动解算，并规划下一段轨迹；在未达到目标点时模型始终按照之前规划的轨迹运动，当运动到目标点时，模型即按照规划的新的一段轨迹运动。如此循环，直至试验结束，完成双体同步分离两条连续轨迹的捕获。

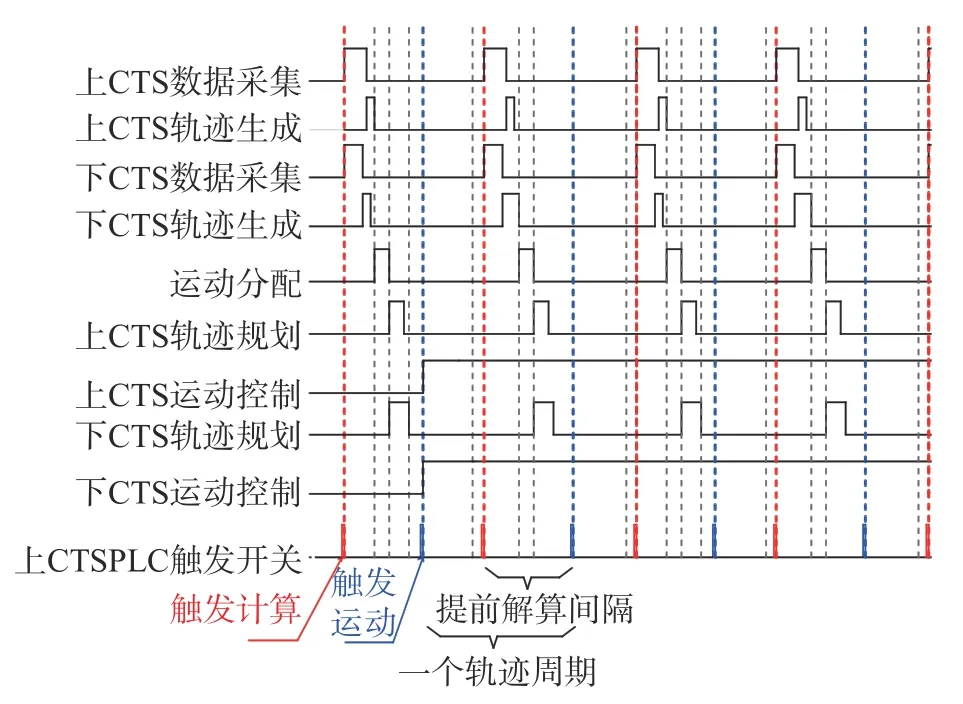
图5 连续轨迹控制时序Fig. 5 Time sequence of the continuous trajectory control

2 风洞试验验证

2.1 试验条件与试验模型

高超声速风洞双体同步捕获轨迹试验技术的验证试验在Φ1 m 高超声速风洞中开展。来流马赫数Ma∞为6、总压p0为1890 kPa、动压q∞为30.17 kPa。表1给出具体风洞运行参数，其中p∞和T0分别为自由来流的静压和总温。

表1 风洞运行参数Table 1 Operation parameters of the wind tunnel

试验模型为TSTO 两级入轨标模[30]的1∶100 几何缩比模型[31]，模型两级质量特性参数如表2 所示。

表2 模型两级质量特性参数Table 2 Mass characteristic parameters of the models

模型一、二级以并联形式组合，图6 给出了置于风洞中的两级模型照片。一级模型通过常规直杆尾支撑正装于下CTS 机构上，二级模型通过弯杆尾支撑正装于上CTS 机构上。模型堵塞度[1]为3.26%，“模型 + 尾支撑”堵塞度为5.14%，“模型 + 尾支撑 +双CTS 机构”堵塞度为8.18%。风洞试验表明，该堵塞度不会造成风洞流场堵塞，满足试验需求。

图6 置于风洞中的试验模型Fig. 6 Test models in the wind tunnel

试验时，两级模型先以各自给定的姿态角和位置处于分离初始位保持不动，风洞流场建立后，再由两级模型天平测量各自气动载荷；通过下位机计算两级各自气动系数，并与外部输入的两级初始条件（如起始位置、角度和速度等）和有关参数（如两级的姿态角、飞行高度、马赫数及两级各自的质量、惯性矩、阻尼导数、推力和弹射力等）一起，通过软件解算全尺寸两级各自6 自由度刚体运动方程，获得两级在初始位置和姿态角下的加速度，并经积分获得一个小的时间间隔（ ∆t）末两级相对巡航级应有的速度、位置和姿态角。本项试验中两级初速度、推力、弹射力均设为0，且不考虑阻尼导数。有侧滑角条件下，两级均需进行x、y、z、θ、ψ、φ6 个自由度的捕获轨迹。由于一级模型所处下CTS 机构不具备z向自由度，且y向自由度本身自重较大，运动不如上机构灵活安全，在满足上机构y向自由度行程的条件下，优先选择以上机构y向运动补偿下机构y向运动。本项试验通过将下机构的z向和y向运动的线位移分配给上CTS 机构的z向和y向运动，以保证两级相对运动位置关系不变，从而同步实现两级各自六自由度捕获轨迹。

2.2 典型流场结构分析

图7 给出了双CTS 试验过程中不同分离时刻的纹影照片，时间间隔Δt′ 为4s。可以看出，两级分离过程中的干扰流动依次表现为分离前的组合体流动、分离启动阶段的缝隙流、分离初期建立的小通道流、分离姿态建立的大通道流。组合体流动（相对初始位模型法向间距与参考长度之比Δy/l＜0.0035）如图7（a）所示，主要是两级主激波的干扰，二级置于一级之上，由于边界层黏性和逆压梯度的存在，二级头部下表面和相应一级上表面之间出现流动分离，并在二级头部前缘产生分离区，进而产生分离激波。缝隙流（0.0035≤Δy/l≤0.0286）如图7（b）所示，两级之间的缝隙没有明显激波反射，但两级之间边界层干扰明显。小通道流（0.0286＜Δy/l≤0.1429）如图7（c～f）所示，当法向间距进一步增大，一级和二级头部激波在两级之间的通道内来回反射形成明显的激波串，这些反射激波在一级和二级表面又会引起流动分离。大通道流（Δy/l＞0.1429）如图7（g～i）所示，当法向间距持续增大，一级和二级头部激波在两级通道内不能形成激波串，但二级头部激波仍然可以入射到一级上表面边界层引起流动分离。此外，由图7 还可以看出带侧滑角后，随着时间的推移，两级各自6 个自由度、共12 个自由度均发生了变化，除了y向变化显著外，受滚转力矩影响两级均发生了明显的滚转，且滚转方向有所不同，一级产生了正滚，二级产生了负滚。

图7 双CTS 试验过程中不同分离时刻纹影照片（α = −2°，β =2°，Δt′ = 4 s，连续轨迹控制模式）Fig. 7 Schlieren images at different separation time instances during the dual captive trajectory test (α = −2°，β = 2°，Δt′ =4 s，under continuous trajectory control mode)

图8 给出了真实分离时间t= 0.49 s 时风洞试验与数值模拟流场的对比，两者流动特征基本一致。

图8 风洞试验与数值模拟流场对比（α = −2°，β = 2°，t = 0.49 s）Fig. 8 Comparison of flow fields between the windtunnel experiment and the numerical simulation(α = −2°，β = 2°，t = 0.49 s)

2.3 试验结果分析

2.3.1 试验精度分析

图9 给出了一、二级初始攻角α= −2°、侧滑角β=2°时，各自法向力系数、俯仰力矩系数随时间变化的三次重复性双CTS 试验结果。图10 以相对初始位全尺寸法向位移与参考长度之比Y/L和俯仰角θ为例，给出了捕获轨迹三次重复性试验结果，图中符号下标1 和下标2 分别表示一级和二级参数。可以看出两级气动力/力矩及分离轨迹均表现较好的重复性。

图9 气动力/力矩系数重复性结果Fig. 9 Repeatability test results of the aerodynamic forces/moments coefficient

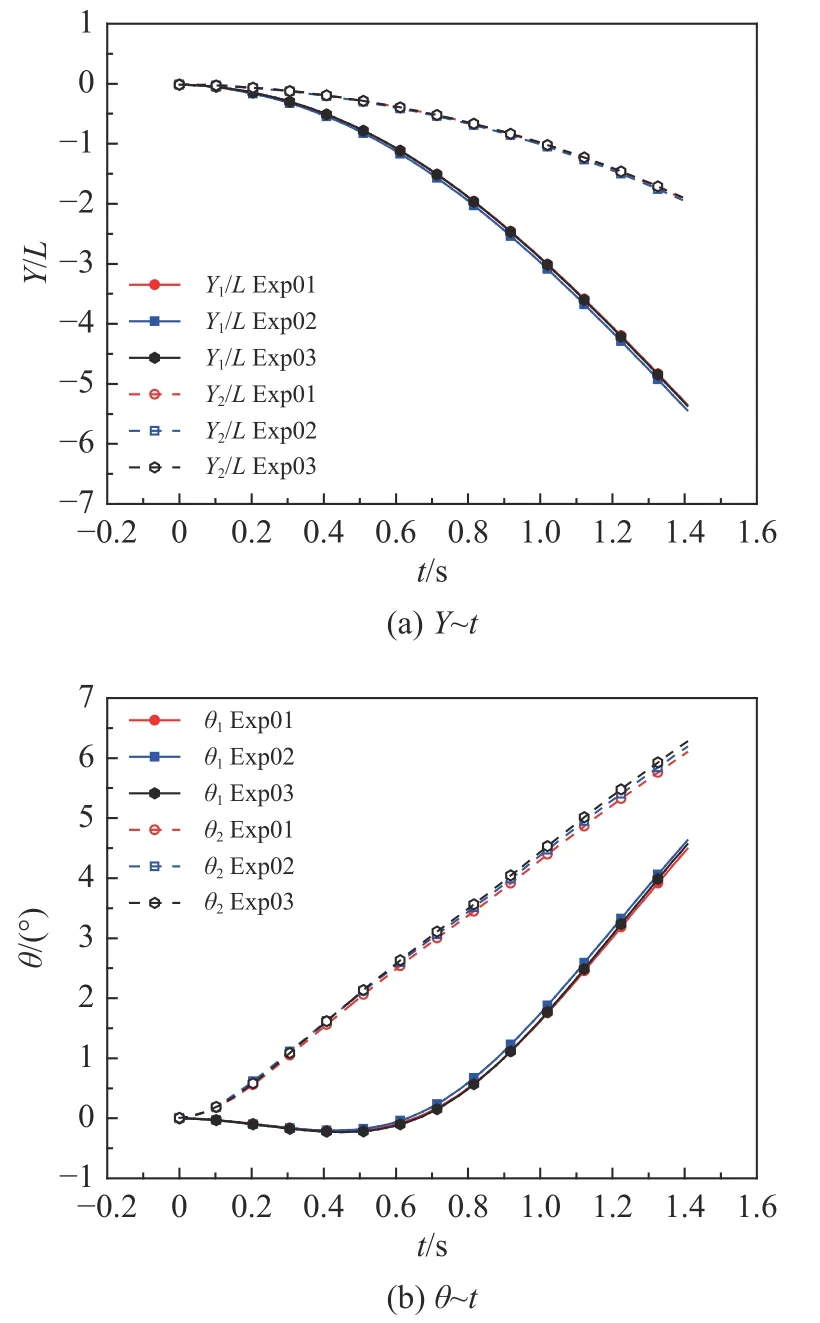
图10 捕获轨迹重复性结果Fig. 10 Repeatability test results of the captive trajectory

表3、表4 按学生氏分布（t分布）置信概率95%[10]给出了连续轨迹控制模式下的双CTS 试验纵向气动力/力矩试验精度σCN/σCmz和纵向轨迹（x向、y向和俯仰方向θ）预测精度（σX、σY、σq）。可以看出，纵向气动力试验精度优于4.8%、力矩优于6.2%，纵向轨迹预测精度优于8.7%。

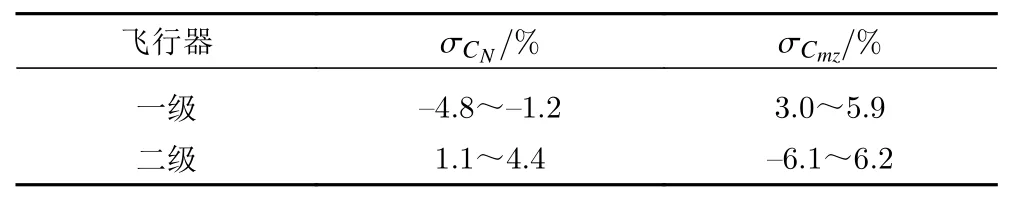
表3 气动力/力矩试验精度Table 3 Aerodynamic force/moment prediction accuracy

表4 轨迹预测精度Table 4 Trajectory prediction accuracy

2.3.2 试验与计算结果对比分析

为了便于结合纹影流动状态进行分离过程中两级气动特性分析，图11 给出了双CTS 试验获得的相对初始位全尺寸两级法向间距与参考长度之比ΔY/L随真实分离时间t的变化曲线，表5 给出了不同分离时间t所对应的不同流动状态。

表5 分离过程中流动状态Table 5 Flow states during the stage separation

图11 全尺寸两级法向间距随分离时间变化(α = −2°，β = 2°)Fig. 11 Time variation of the vertical spacing between the two stages in full scale (α = −2°，β = 2°)

图12 和图13 给出了双CTS 试验和计算获得的分离过程中全尺寸两级气动特性随分离时间变化的结果对比，试验和计算均考虑了重力影响。

图12 一级气动力/力矩系数随分离时间变化（α = −2°，β = 2°）Fig. 12 First stage force and moment variations with time(α = −2°，β = 2°)

图13 二级气动力/力矩系数随分离时间变化（α = −2°，β = 2°）Fig. 13 Second stage force and moment variations with time(α = −2°，β = 2°)

从试验与计算结果结合试验纹影可以看出，1.1 s 的真实分离时间里，ΔY/L增加至2.27，两级分离经历了组合体流动、缝隙流动、小通道流动和大通道流动。在初始组合体流动状态时（t＜0.12 s），随着分离时间增加即分离距离的逐渐增大，一级法向力负向增大，低头俯仰力矩有所减小，二级法向力正向增大，抬头俯仰力矩明显减小。在缝隙流阶段（0.12 s≤t＜0.39 s），二级下表面和一级上表面的边界层相互干扰严重，随着级间距的拉开，边界层/边界层干扰减弱，两级各气动力系数按原有组合体流动时的变化趋势随时间近线性变化。而到了小通道流阶段（0.39 s≤t＜0.86 s），两级级间区域因激波在物面上来回反射形成激波串，此时级间干扰尤为复杂，包括激波/激波干扰、激波/边界层干扰等流动现象，导致了两级各气动力系数的非线性变化，尤其是俯仰力矩变化波动显著。随着级间距进一步拉大至大通道流时（t＞0.86 s），两级之间干扰逐渐减弱，已无激波串形成，各气动力系数变化也趋于线性。

风洞试验和数值计算获得的两级模型的气动特性随分离时间的变化趋势基本一致，但在量值上还有一定差异，尤其是初始分离阶段。造成偏差的主要原因除试验存在支撑干扰影响外，气动载荷导致模型弹性变形所带来的两级模型之间的位置和姿态偏差也会使风洞试验和数值计算状态的初始符合度变差。

为分析法向间距对两级气动特性的影响，图14 给出了网格测力试验中，相对初始位不同模型法向间距Δy时，一、二级俯仰力矩系数Cmz1和Cmz2的变化曲线。可以看出在分离初始阶段，Δy的小量变化可以造成两级俯仰力矩系数的显著变化。如Δy仅由0 变到5 mm，Cmz1则由−0.00275 变到−0.00136，变化量达50.5%；而Cmz2则由0.0276 变到0.00966，变化量达65%。

图14 两级俯仰力矩系数随模型法向间距变化（α = 0°，β = 0°）Fig. 14 Pitch moments of the two stages variations with the vertical spacing (α = 0°，β = 0°)

因此不难理解，任何初始扰动造成的初始法向间距Δy小量变化都会造成俯仰力矩系数的较大偏差。这是造成试验和计算俯仰力矩结果初始差异显著的主因之一，也为今后试验技术的改进明确了方向。

图15 和图16 给出了试验和计算获得的分离过程中相对初始位全尺寸两级各自分离轨迹。可以看出，两者的分离规律一致性较好，一级俯仰方向经历了先低头再抬头的过程，二级俯仰方向始终保持抬头趋势；整个分离过程中，二级相对一级X方向上向前、Y方向上向上，两级滚转角均发生较大变化，一级正滚16°，二级负滚4°。两级在当前初始攻角−2°、侧滑角2°时，仅依靠气动力可以实现正常分离。

图15 一级分离轨迹（α = −2°，β = 2°）Fig. 15 Separation trajectory of the first stage (α = −2°，β = 2°)

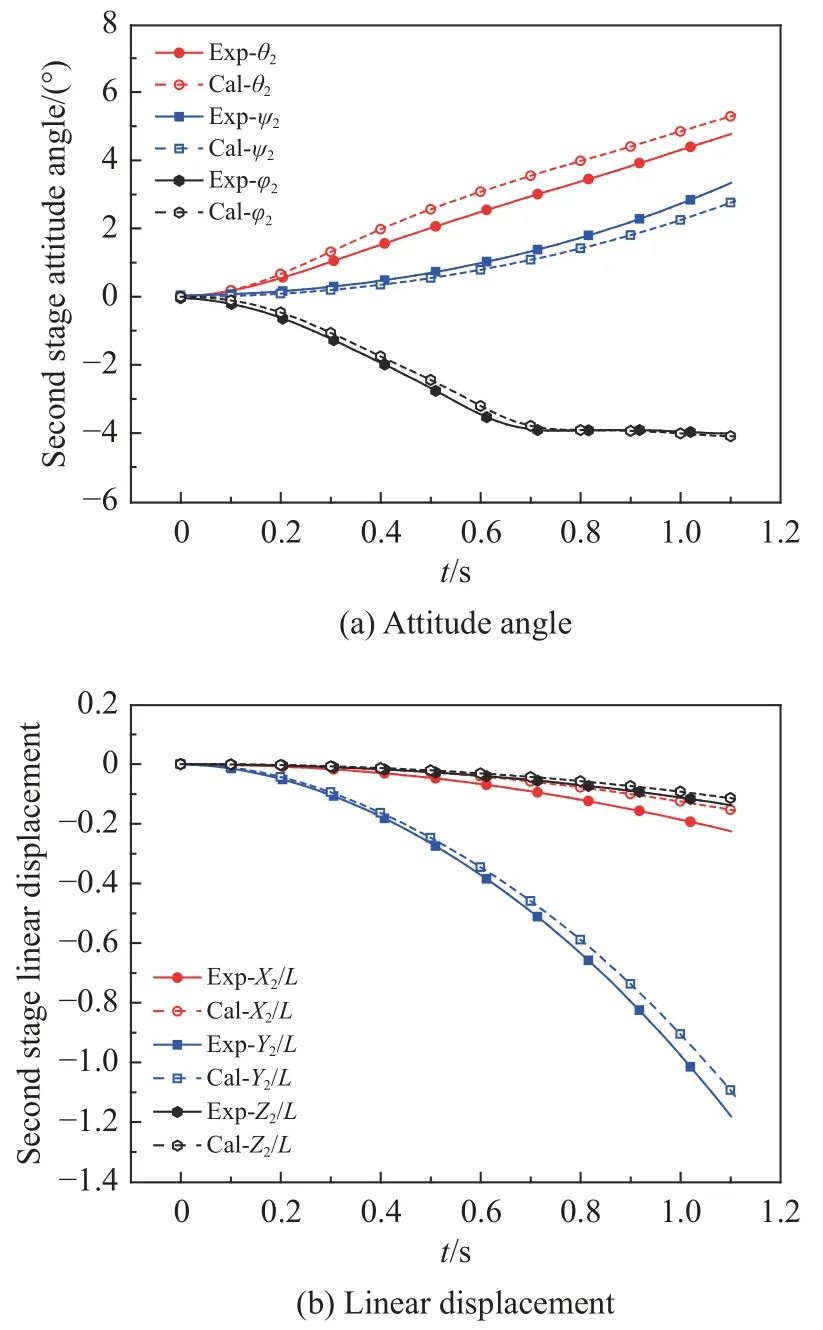
图16 二级分离轨迹（α = −2°，β = −2°）Fig. 16 Separation trajectory of the second stage(α = −2°，β = −2°)

3 结 论

本文针对高超声速飞行器多体分离地面模拟问题、研发了高超声速风洞双体同步捕获轨迹试验技术，建立了Φ1 m 高超声速风洞双体同步分离试验平台。首次实现了适用于两体均有较大位姿变化的高超声速风洞双体同步分离共12 个自由度的捕获轨迹，开展了马赫数6 的双体同步分离捕获轨迹技术验证试验，获得了高超声速两级入轨并联分离标模级间分离典型状态的一、二级干扰气动特性及分离轨迹。验证结果表明，建立的高超声速风洞双体同步捕获轨迹试验技术较好地获得了飞行器两级气动特性及分离轨迹，纵向气动力试验精度优于4.8%、力矩优于6.2%，纵向捕获轨迹预测精度优于8.7%，可以满足高超声速飞行器两级分离过程中均有较大位姿变化的分离模拟。试验与计算结果对比表明，两者在规律上表现出较好的一致性，但在量值上仍有一定差异，尤其是俯仰力矩系数方面。从分析来看，分离初始阶段，两级俯仰力矩系数变化受法向间距Δ y 变化影响较大。

下一步将在本文研究基础上，开展高超声速双体捕获轨迹过程中支撑干扰影响实时修正技术研究、高超声速双体捕获轨迹风洞试验数据非定常效应修正方法研究及有控双体捕获轨迹试验技术研究等。

致谢：感谢中国航天空气动力技术研究院沈清、陈兰、胡静等在TSTO 标模多体分离特性研究中的支持，感谢中国空气动力研究与发展中心计算空气动力研究所龚小权、贾洪印、赵辉等在数值模拟工作中做出的贡献。