TSTO 级间分离气动特性数值仿真分析
龚小权,贾洪印,赵 辉,唐 静,张 健,*,付云峰
(1. 中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000;2. 空气动力学国家重点实验室,绵阳 621000)
0 引 言
重复使用[1]是天地往返飞行器大幅降低发射成本、减小发射周期、提高航天应用的重要措施。一方面,可重复使用航天飞机及空间轨道机动飞行器X-37B 的成功试飞使得火箭基两级入轨(two stage to orbit, TSTO)重复使用成为较为现实的飞行模式。另一方面,随着吸气式冲压发动机的技术进步,使用涡轮/吸气冲压组合动力的一级飞行器水平起降TSTO重复使用飞行方案也逐步取得突破性进展。
冯毅等[2]、唐伟等[3]提出基于TBCC 动力的TSTO 气动布局概念设计,综合考虑两级分离安全性,将双垂尾外移并适当偏转为V 尾,同时适当增大下折翼梢以更大程度地利用超声速、高超声速激波升力,并增加航向稳定性;通过不断迭代优化,最后获得一级飞行器垂尾下反方案,同时调整二级飞行器的质心位置至64%附近,以进一步拓宽分离边界。
TSTO 并联飞行器级间分离是其设计时必须考虑的关键问题之一。两级飞行器外形尺寸巨大且重量为数百吨量级。以唐伟设计的TSTO 为例,一级飞行器长度约85 m,二级飞行器长35 m,重量都在百吨以上。一方面,分离中如果两级接触,接触力极有可能破坏飞行器结构或防热层。另一方面,分离初始时刻两级级间距离相当近,只有300 mm,相对两级的尺寸来说太小,略微俯仰过快就会带来头部或者体襟翼的碰撞,这对分离初始阶段两级飞行器的姿态控制提出了较大要求。另外TSTO 两级飞行器都是升力体布局,在一定的攻角范围内两级都有较大的升力,且升力与重力同一量级,这将导致两级不易分开,进一步增加了两级碰撞的风险。TSTO 并联分离两级完全分开的时间很长,从能量管理角度考虑,设计师希望分离过程平稳,尽量减少高度及能量损失。因此研究TSTO 并联分离过程对TSTO 外形设计、分离点选择及分离方案设计至关重要。
Liu 等[4]研究了TSTO 在不同速度下的分离,分析了组合体在超声速以及不同襟翼偏角下的气动特性,研究了不同马赫数下无侧滑角的纵向分离。采用国家数值风洞工程通用CFD 软件NNW-FlowStar[5],本文研究了TSTO 飞行器在有侧滑角时的并联级间分离过程,给出了分离过程一二级的姿态角及质心位移,并与试验值进行了对比;分析了分离过程的安全性,验证了FlowStar 软件数值模拟TSTO 类并联分离的能力和精度。文章主要由四个部分组成:首先是数值模拟方法简介,介绍数值模拟软件NNW-FlowStar、数值模拟用到的技术以及六自由度求解方法;然后在第二部分重点介绍TSTO 并联分离的计算数模、网格,并采用WPFS 标准算例验证了软件的非定常计算精度;第三部分是分离安全性分析,首先分析了TSTO 组合体气动特性,给出了TSTO 可能安全分离的分离点,然后数值模拟了在马赫数Ma= 6、来流攻角α= −2°、侧滑角β= 2°、高度H= 30 Km 时,TSTO的并联分离过程,分析了分离中两级飞行器的姿态角变化及质心位移。最后对全文进行了总结。
1 数值方法
1.1 软件介绍
数值模拟软件为中国空气动力研究与发展中心基于国家数值风洞工程研发的通用CFD 软件NNWFlowStar。该软件内核MFlow 是基于非结构混合网格、用于求解亚跨超声速流场的专业CFD 求解器[6-9]。NNW-FlowStar 能处理任意形状的网格单元,具有较强的灵活性。采用有限体积法离散控制方程,求解变量存储于网格单元的体心。在本文数值模拟中,对流通量采用Roe 通量差分分裂格式进行离散,该格式具有很高的间断和黏性分辨率[10-11]。单元内使用线性重构使得空间离散具有二阶精度,变量梯度求解使用节点型Gauss 方法[12],限制器采用Venkatakrishnan[13]限制器,该限制器具有较高的精度和良好的残差收敛性。粘性通量采用中心差分离散。假定流场为全湍流,采用Spalart-Allmaras 一方程湍流模型[14],湍流模型方程空间离散采用一阶迎风格式。
守恒形式的非定常Navier-Stokes(N-S)方程为:其中,为守恒变量,H为无黏通量,Hv为黏性通量,n表示控制体单元边界面的外法矢。
采用双时间步方法求解整个非定常过程,由于非定常计算工作周期较长,本文内迭代采用LU-SGS(lower upper-symmetric Gauss-Seidel)隐式时间离散[15],并在迭代中引入局部时间步长加速收敛技术加速收敛。采用基于MPI (message passing interface) 的大规模并行计算[16]缩短计算周期。重叠挖洞及插值相关技术见文献[17]。
1.2 六自由度求解
FlowStar 软件在初始状态的机体体轴系中求解分离物体的质心运动方程,在分离物体的体轴系(非惯性系)中求解分离物体的绕质心运动方程。采用四阶R-K 方法求解分离物体的运动方程(2)~方程(4),得到质心的速度以及物体的角速度,从而得到物体的姿态角。
其中,φ为滚转角,θ为俯仰角,ψ为偏航角,MA表示气动力力矩,MT表示除气动力外的其他力的力矩(外力力矩)。
2 计算模型、网格及软件验证
2.1 计算模型
本文研究模型是大型TSTO 并联飞行器,由唐伟设计提供。图1 给出了该模型的三视图,下面级长度为80 m,重心距离下面级飞行器实际头部尖点(55.45,0,−1.07)约65%自身长度位置;上面级长度为35 m,重心距离下面级飞行器实际头部尖点(55.45,0,4.00)约64%自身长度位置。两级间最短距离0.3 m。详细尺寸及质量特性见文献[3-4]及表1。
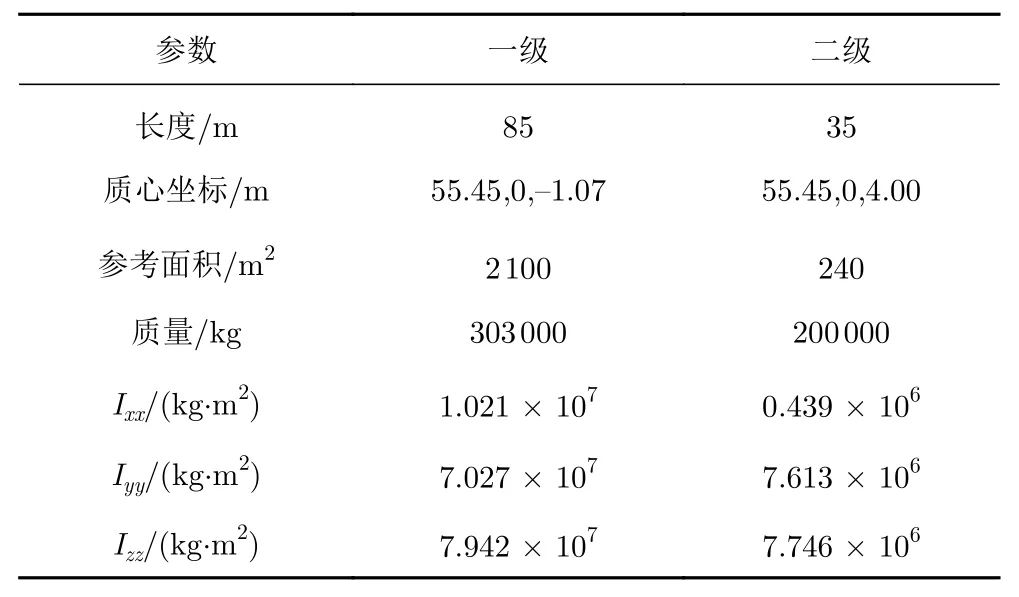
表1 TSTO 尺寸及质量特性Table 1 Geometry size and mass characteristics of TSTO
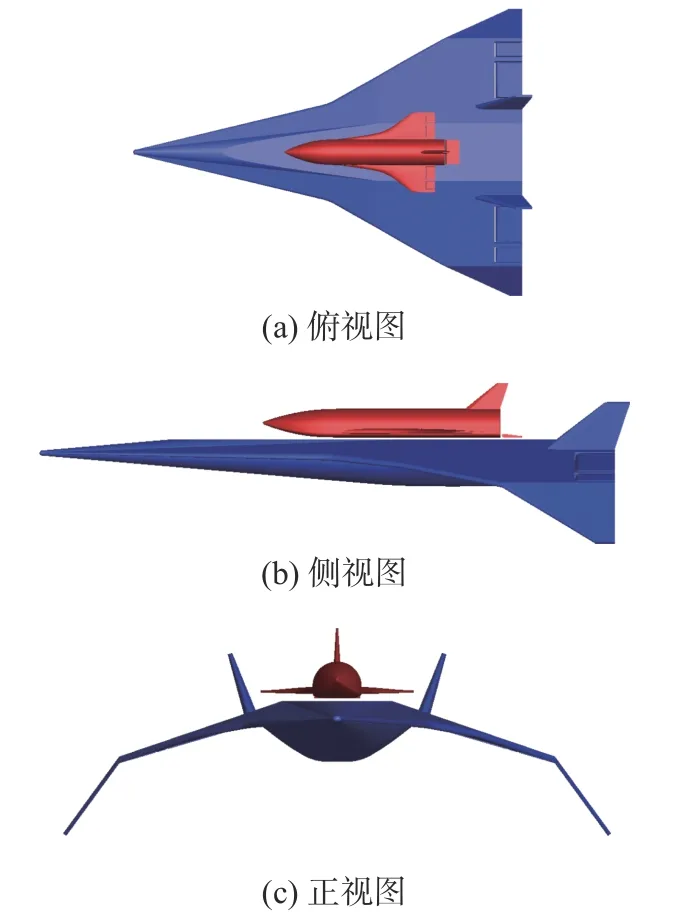
图1 TSTO 外形三视图Fig. 1 Three views of the TSTO
2.2 计算网格
本文的计算网格为非结构混合网格,包括六面体、三棱柱、金字塔、四面体网格。采用六面体和三棱柱模拟附面层,四面体模拟空间流场各向同性区域,通过金字塔过渡三棱柱和四面体。为节省网格量并较好地模拟前缘,在两级飞行器机翼、垂尾表面前后缘尽可能采用四边形网格,并将四边形网格的长宽比控制在100 以内。对于一些规则且独立的部件,例如体襟翼、副翼、升降舵表面,全部采用结构四边形网格布置,如图2、图3。图2 给出了TSTO 一级的表面网格,图3 给出了二级的表面网格。从图中看到,在两级表面外形变化较大的区域都有加密网格,以保证计算网格与数模的一致性。针对二级翼身组合体外形,在机翼机身连接处加密网格。

图2 TSTO 一级表面网格Fig. 2 Surface grid of the first stage of TSTO

图3 TSTO 二级表面网格Fig. 3 Surface grid of the second stage of TSTO
图4 给出了TSTO 一二级分离初始时刻空间网格的y= 0 截面。从图中看到,为保证重叠网格插值精度,将一级飞行器空间区域中二级飞行器可能的运动区域的空间网格加密(图中外层较大的加密区)。
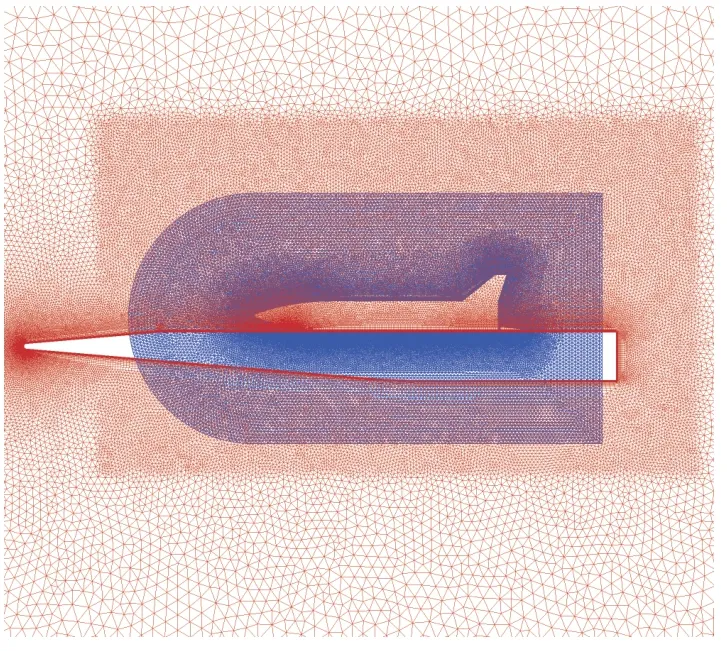
图4 一二级分离初始时刻对称面网格Fig. 4 Grid distribution in the symmetry plane at the initial time instance of separation
TSTO 一二级距离非常近,仅0.3 m,且分离的马赫数Ma= 6,在一级机身上表面和二级机身下表面存在严重的激波边界层干扰以及激波反射。因此针对TSTO 一级机身上表面和二级头部及机身下表面进行网格局部加密,如图5、图6,以期更好地捕捉两级间的激波反射,提高对气动特性的模拟精度。
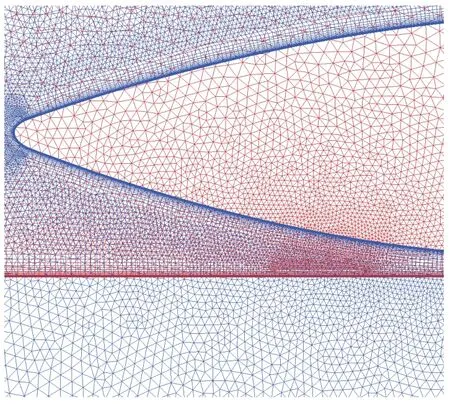
图5 二级头部附近对称面网格Fig. 5 Grid distribution around the nose of the second stage in the symmetry plane
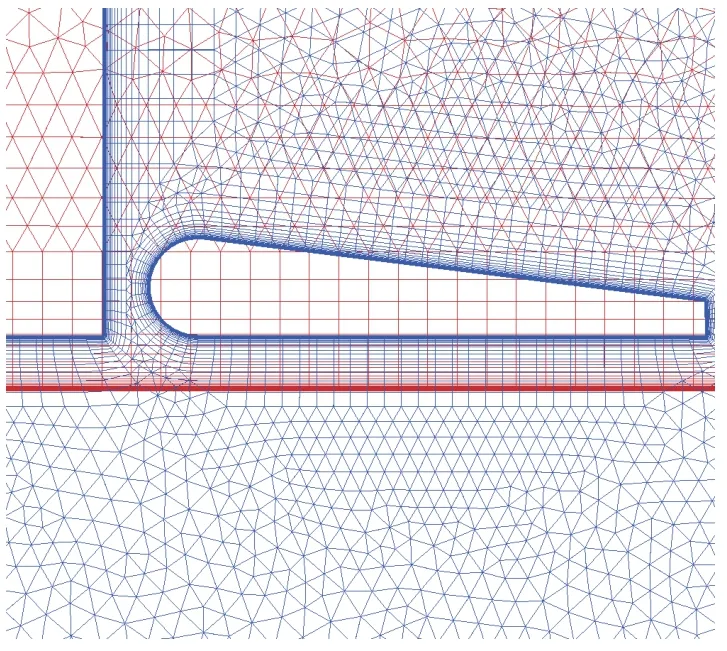
图6 两级机身缝隙间的对称面网格Fig. 6 Grid distribution around the two-stage fuselage gaps in the symmetry plane
2.3 WPFS 模型分离数值模拟
机翼/挂架/带舵外挂物模型WPFS(wing/pylon/finned-store)[18]是美国发起第一次分离投放CFD 验证时使用的一个机翼和导弹的简化模型。该模型具有比较翔实的风洞数据,因此被各种CFD 软件用做验证分离计算的标准算例。图7 给出了WPFS 模型视图。为确保外挂物和机翼/挂架的安全分离,试验过程中使用了虚拟的弹力作用,在分离距离大于给出的安全距离后,虚拟弹力的作用消失。试验条件、外挂物质量特性和虚拟弹力的相关参数见文献[18]。

图7 WPFS 模型Fig. 7 WPFS model
包裹机翼和挂架的背景网格有网格单元239 万,其中四面体183 万、三棱柱56 万;包裹外挂物的子网格有网格单元208 万,其中四面体101 万、三棱柱107 万。采用非定常雷诺平均N-S 方程、SA 湍流方程来模拟计算该模型的外挂物分离历程。计算条件和CTS (captive trajectory simulation)试验条件相同,计算中真实时间步长取0.01 s。通过计算得到了外挂物质心位置、外挂物姿态角随时间变化曲线。
图8 给出了计算得到的带舵外挂物质心位置与试验结果的对比曲线。计算结果和试验值吻合很好。
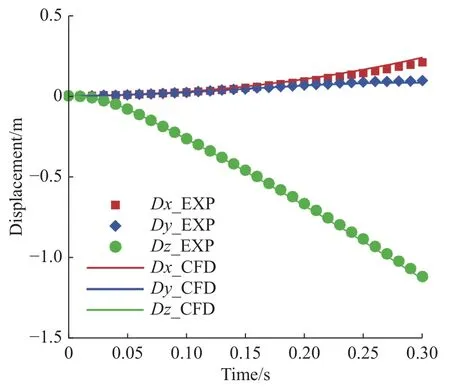
图8 计算和试验的外挂物质心随时间变化对比Fig. 8 Displacement variation with time for the centroid of the external store (computation VS experiment)
图9 给出了计算得到的带舵外挂物姿态角与试验结果的对比曲线。计算得到的外挂物姿态角中的偏航角和滚转角与试验结果吻合得较好;但俯仰角却比试验值偏大,在0.3 s 时最大偏差值有0.8°(约19%)。分析其原因可能是数值模拟直接选择了在0.054 s 时取消弹射力,和试验中严格地根据距离取消弹射力有一定差别,这种累计效应随着时间的增长显现了出来。
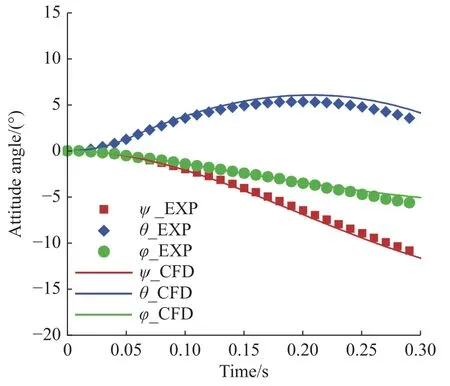
图9 计算和试验的外挂物姿态角随时间变化对比Fig. 9 Attitude angle variation with time for the external store(computation VS experiment)
通过计算结果和试验结果的比较分析可以看出,计算结果与试验数据吻合得较好,表明FlowStar 软件的数值方法和非结构重叠网格方法的可靠性较高,具有较强的实用性,能够较好地模拟多体干扰与分离复杂流场及物体分离投放轨迹。
3 分离安全性分析
3.1 组合体气动特性分析
TSTO 两级飞行器安全分离对于整个方案设计至关重要。一方面,TSTO 两级飞行器都是升力体布局,且分离初始时刻相距很近,这对分离方式提出了较高的要求;另一方面,从能量管理角度,设计师期望正攻角下分离,从而避免TSTO 高度及能量损失。因此研究TSTO 设计分离工况点(Ma= 6,H= 30 Km)的分离特性异常重要。
本节首先分析了TSTO 组合飞行器在设计分离工况的定常气动特性,用于选择分离点。图10 给出了组合体一二级升力系数随来流攻角变化的曲线,从图中可以看到,一级飞行器升力系数随着攻角增大而增大,攻角大于1°之后升力系数为正。二级飞行器在计算的攻角内升力都为正值,二级飞行器完全处于一级飞行器的背风区,其升力系数随着攻角增大而减小。图11 给出了组合体一二级飞行器俯仰力矩系数随来流攻角变化的曲线,在计算的攻角范围内一级飞行器的俯仰力矩都是负值,二级飞行器的俯仰力矩都是正值,这代表分离初始阶段两级会相对旋转,而不是同向旋转,这对分离极为不利。从图10、图11 看到,在计算的攻角范围内都是不利于分离的。二级具有较大的抬头力矩,由于两级间距离很小,初始距离为0.3 m,过大的抬头力矩容易导致一二级相撞。

图10 一二级升力系数随攻角变化曲线Fig. 10 Lift coefficient variation with the angle of attack for the two stages
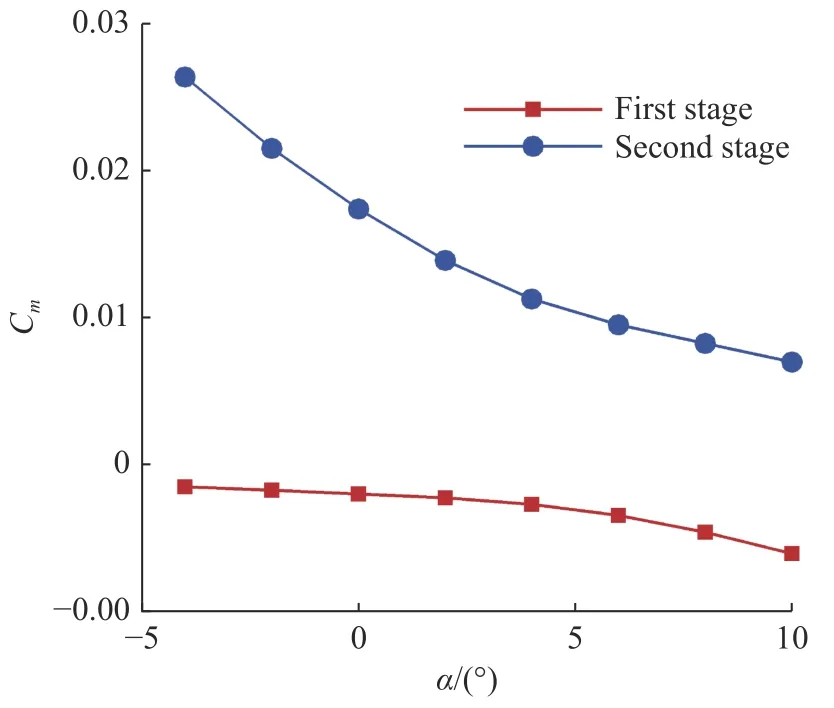
图11 一二级俯仰力矩系数随攻角变化曲线Fig. 11 Pitching moment coefficient variation with the angle of attack for the two stages
表2 给出了一二级舵面不偏转时的定常气动特性。从表中看到,在来流攻角为−2°、0°、2°时,一级的总的法向力(气动力加重力)都为负,二级的总的法向力(气动力加重力)为负。因此在这三个攻角下分离一、二级都要损失高度和能量。从表2 中还可以看到,在攻角为−2°时,二级法向力最大,一级法向力最小,单从这方面考虑,此状态是最有利于分离的;但是此时二级的俯仰力矩较大,从这个方面看,该状态又不利于分离。
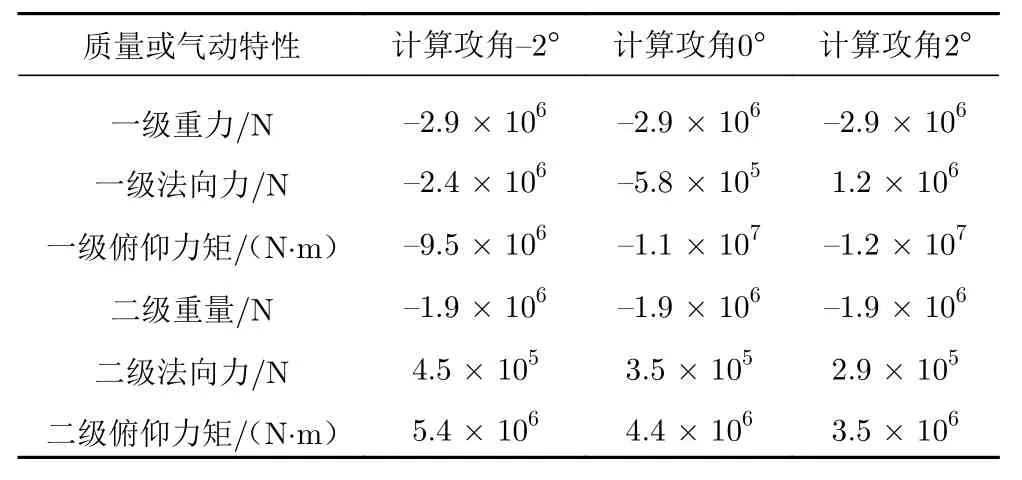
表2 无舵偏定常气动力Table 2 Steady aerodynamic forces without rudder deflection
3.2 分离过程模拟
从3.1 节的分析看到,在计算攻角内分离都不是特别理想,但是这只是初始状态。随着分离进行,两级间距离逐渐增大,两级间复杂的激波干扰以及两级相对位置、姿态的变化也导致两级的气动特性急剧变化。
本节选取来流攻角−2°,侧滑角2°来分析两级的级间分离过程。计算采用两套网格,如图4 所示,包括包裹一级飞行器的网格和包裹二级飞行器的网格。包裹一级飞行器的网格量约为2122 万,其中,四面体网格单元1254 万个、三棱柱单元472 万个、六面体单元342 万个、金字塔单元54 万个。包裹二级飞行器的网格量约为1288 万,其中四面体网格单元623 万个、三棱柱单元448 万个、六面体单元179 万个、金字塔单元38 万个。CTS 试验在中国空气动力研究与发展中心Φ1 m量级高超声速风洞FD-30 中进行[19]。该风洞在2019 年建成双轨迹捕获试验系统,具备开展Ma= 6 并联分离双分离轨迹捕获试验的能力。为减少支撑干扰影响,试验采用双尾支撑结构,如图12。图13 给出了CTS 试验中的典型流场纹影图,从图中能够看到,级间分离过程中两级间存在复杂的激波干扰以及激波边界层干扰。试验在求解六自由度方程时,将滚转力矩Mx置零,也就是将方程(3)中的滚转力矩置零。为与试验一致,计算过程也采用相同的处理。计算来流条件为Ma= 6、α= −2°、β= 2°、H= 30 Km,采用全尺寸外形,在中国空气动力研究与发展中心计算集群上采用1024 核完成整个非定常计算。

图13 CTS 典型流场纹影图[19]Fig. 13 Schlieren image of the typical flowfield in CTS[19]
图14 、图15 给出了TSTO 两级在分离过程中两级姿态角随分离时间变化的曲线。在计算的分离时间内两级能够安全分离,计算和试验的俯仰角和偏航角随时间变化具有很好的一致性,进一步验证了NNW-FlowStar 的数值模拟精度。从图14 一级飞行器的姿态角变化曲线看,计算和试验获得的偏航角和滚转角变化规律完全一致。在2°侧滑角下,一级飞行器具有正偏航角,头部逐渐转向来流侧滑方向,减小侧滑角;由于滚转力矩置零,滚转角很小。一级飞行器在分离初始阶段具有较小的低头力矩,随着两级的移动,尤其是一二级法向方向的位移,导致二级的头激波及其反射激波在一级上表面的位置后移,一级飞行器俯仰力矩逐渐增大,并逐步抬头。
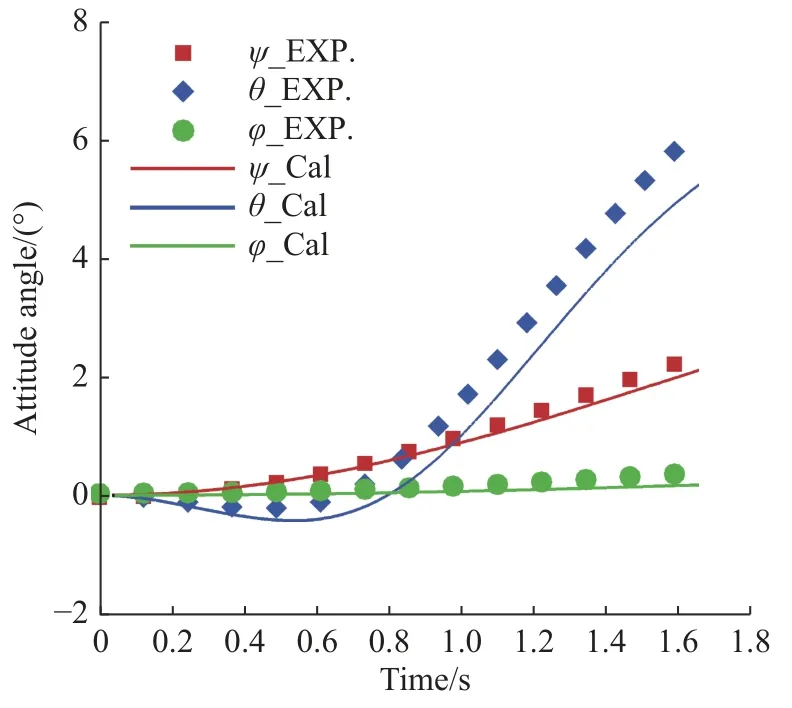
图14 Ma = 6、α = −2°、β = 2°,一级飞行器姿态角随时间变化曲线Fig. 14 Attitude angle variation with time for the first stages at Ma = 6,α = −2°,β = 2°
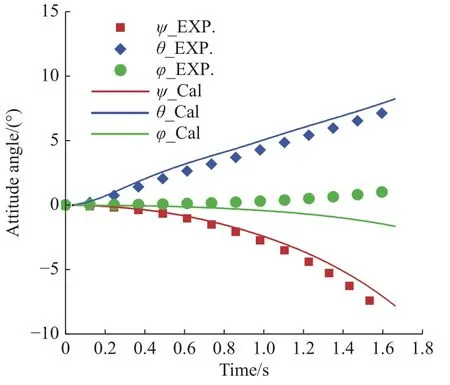
图15 Ma = 6、α = −2°、β = 2°,二级飞行器姿态角随时间变化曲线Fig. 15 Attitude angle variation with time for the second stages at Ma = 6,α = −2°,β = 2°
从图15 的二级姿态角变化曲线看,计算和试验的二级俯仰角和偏航角变化规律一致。在上一节中分析组合体的气动特性时看到,二级飞行器具有较大的抬头力矩,因此在分离过程中二级飞行器一直保持抬头,且抬头较快;随着两级的分离,二级飞行器的头激波的反射激波逐步后移且强度逐步减弱,影响二级飞行器机身和机翼下表面压力分布,导致俯仰力矩斜率变化。二级飞行器具有负偏航角,头部逐渐转向来流侧滑的反方向,增大侧滑角。
图16、图17 给出了一二级飞行器质心位移随时间变化曲线。在2°侧滑角下,两级飞行器均向飞行员左侧移动,计算与试验的两级侧向移动位移变化规律及大小一致。从图16、图17 看到,一二级飞行器均向下运动,计算与试验的两级质心法向位移变化规律及量值一致。由于一级飞行器为负升力,二级飞行器为正升力,因此相同时间时,一级向下运动距离更大。试验和计算的轴向位移有一定差别,随着分离进行,两者的差量增大。在1.6 s 时刻一级飞行器计算和试验的轴向位移相差约1.5 m,这与阻力计算精度相关;而阻力计算精度又与计算网格尺寸、湍流模型、两级后体分离等多种因素相关。但总的来说,相比飞行器尺寸(85 m),这一差量较小。

图16 Ma = 6,α = −2°,β = 2°,一级质心位移随时间变化曲线Fig. 16 Displacement variation with time for the centroids of the first stages at Ma = 6,α = −2°,β = 2°
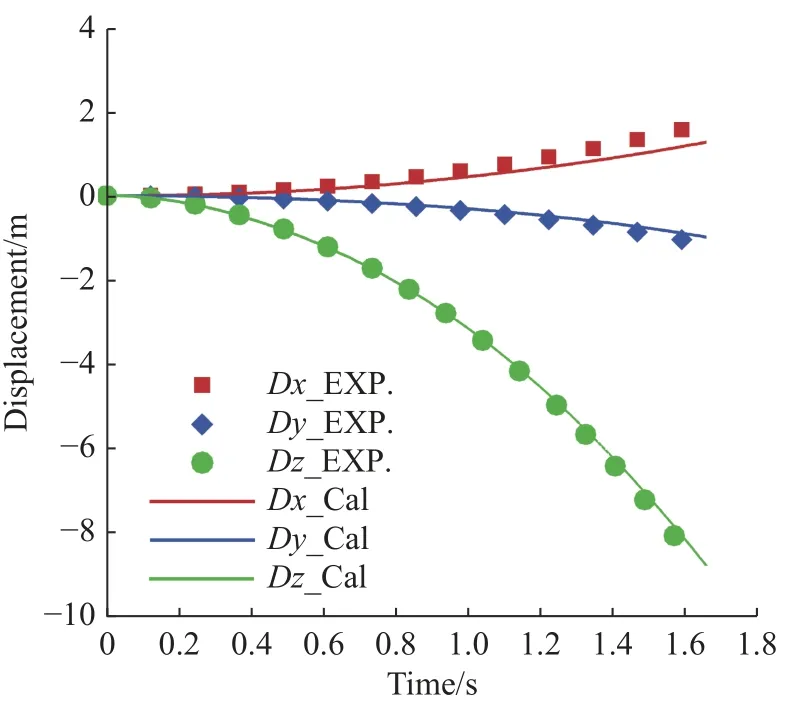
图17 Ma = 6,α = −2°,β = 2°,二级质心位移随时间变化曲线Fig. 17 Displacement variation with time for the centroids of the second stages at Ma = 6,α = −2°,β = 2°
图18 给出了Ma= 6、α= −2°、β= 2°,TSTO 两级并联分离不同分离时刻两级对称面的压力云图以及表面俯视图。分离过程两级间流动复杂,二级飞行器的头部激波打到一级飞行器上表面并在二级飞行器机身下表面和一级飞行器上表面之间反射。在分离的初始阶段,一二级飞行器的最小距离出现在二级体襟翼附近,二级飞行器体襟翼下表面出现高压。随着分离时间增大,二级头激波在一级上表面的位置逐步后移,一级上表面的高压区逐步后移。在计算的时间范围内两级仍未相互脱离干扰区。
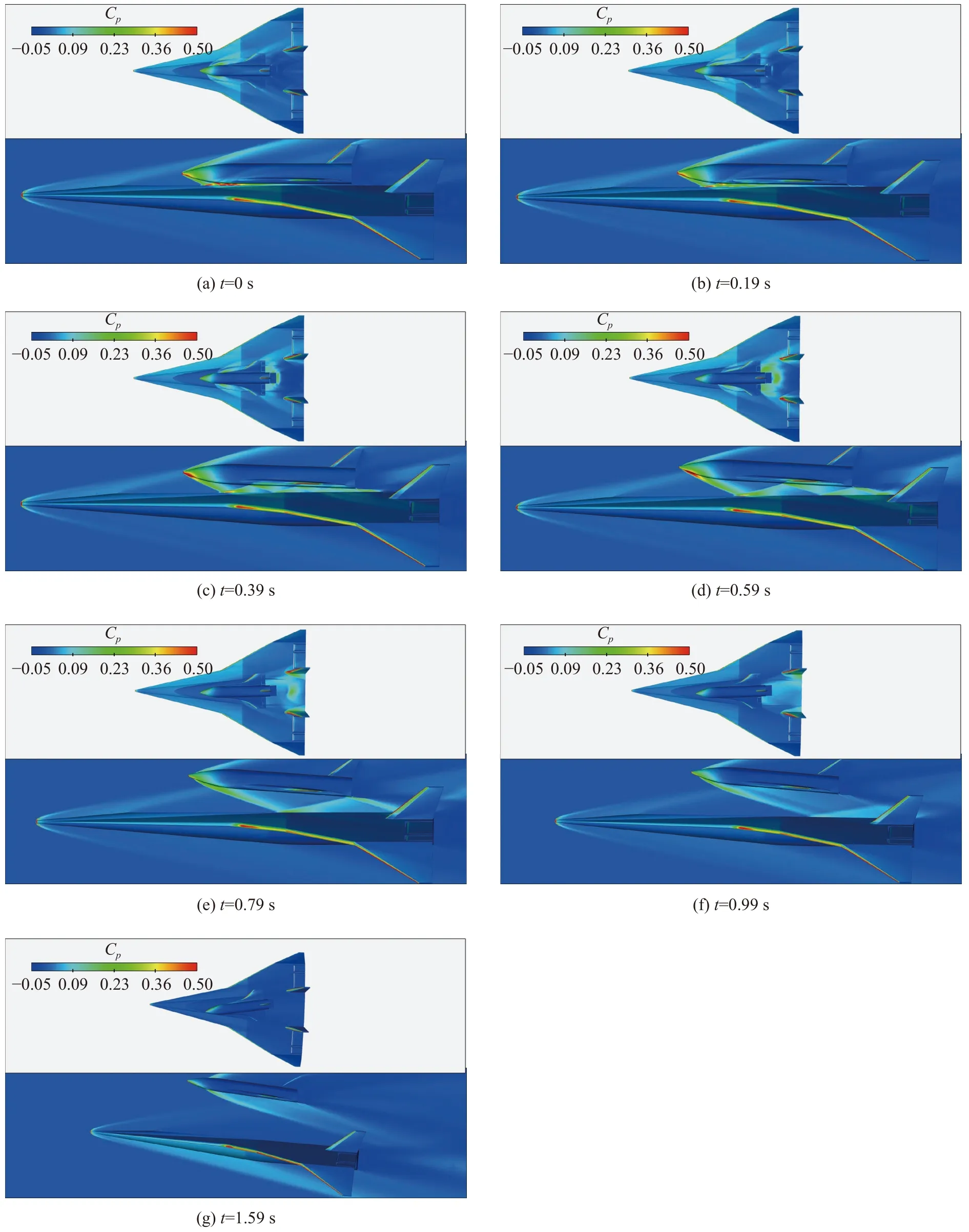
图18 Ma = 6、α = −2°、β = 2°,不同时刻两级对称面及表面压力云图Fig. 18 Pressure distributions in the symmetry plane and on the surface of the two stages at different time instances for Ma = 6,α = −2°,β = 2°
4 结 论
本文基于国家数值风洞工程通用CFD 软件NNW-FlowStar,采用各向异性的非结构混合网格以及动态重叠网格数值模拟了TSTO 一二级飞行器并联分离。通过与CTS 试验值对比一二级飞行器质心位移以及姿态角变化曲线,验证了软件对升力体并联级间分离类问题的数值模拟能力。通过数值模拟,可以得到以下结论:
1)NNW-FlowStar 软件在重叠插值算法、高分辨率Roe 格式、高斯节点型梯度计算方法、大规模并行等一系列数值算法方面的开发和改进保证了高超声速流场的精细模拟。
2)NNW-FlowStar 软件具备开展TSTO 升力体并联级间分离类数值模拟能力,模拟结果与CTS 试验值具有较高的一致性,验证了软件在高超飞行器并联分离数值模拟的精度。
3)TSTO 并联级间分离关系到两级飞行器设计,目前的分离工况能够安全分离,但是安全余量非常小,分离中两级最小距离出现在二级体襟翼处,如果考虑到两级飞行器尺寸、气动弹性以及其他因素,这种最小距离是不安全的。
4)需要进一步研究TSTO 并联级间分离方案,包括来流攻角、预置舵偏等,以期能够增加分离过程两级的安全距离,在减少TSTO 能量损失的同时,实现两级快速分离。
致谢:感谢中国空气动力研究与发展中心林敬周研究员提供的CTS 试验数据。

