TSTO 并联分离激波/边界层干扰流动特性分析

范孝华，张庆虎，罗 磊，林敬周，唐志共

(1. 中国空气动力研究与发展中心 超高速空气动力研究所，绵阳 621000；2. 中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000；3. 中国空气动力研究与发展中心，绵阳 621000)

0 引 言

两级入轨飞行器（two-stage-to-orbit, TSTO）是一种可重复使用的航天运载器（reusable launch vehicle,RLV），能够实现高频快速进出空间，遂行不同类型的飞行任务，大幅降低航天运输成本。其作为极具潜力的空天运输系统，一直受到国内外广泛关注[1-8]。

级间分离问题直接决定了飞行任务的成败，是TSTO 飞行器必须解决的关键问题[9]。助推级与轨道级并联布局的TSTO 级间分离马赫数一般设计在超声速或者高超声速范围[10]，分离过程需要经历组合体流动、缝隙流、小通道流、大通道流，直至无干扰流动，其间涉及三维激波/激波干扰以及激波/边界层干扰等复杂流动。这些复杂流动会引起飞行器表面的边界层流动状态以及压力和热流载荷急剧变化，进而对两级飞行器分离过程的气动特性产生显著影响，甚至可能破坏飞行器表面、威胁分离的安全性，导致事故发生。深入理解和认识TSTO 级间产生气动干扰的流动机理，探索削弱气动干扰强度的途径，可以为飞行器气动设计以及分离方案的选择提供有益参考。

Ozawa 等[11]采用半球-圆柱模型作为轨道级，助推级则分别选择三角翼以及构型更工程化的高超声速助推级模型，通过风洞试验获取马赫数8.1 模型周围的流场特征以及模型壁面热流分布；研究发现高超声速助推级模型前缘产生了强的头激波，增加了流过气流的总压损失，进而削弱了两级模型间的激波/激波和激波/边界层干扰强度。Uematsu 等[12-14]同样选择半球-圆柱模型作为轨道级，而助推级则采用截面分别为方形、圆形以及三角形的细长体模型，在马赫数4 条件下开展不同级间距的试验与数值研究；分析了模型周围流场结构、模型表面压力分布以及气动力特性，发现横截面为三角形的助推级对反射激波的减弱效应最强，进而使得级间的干扰强度下降最多。王粤等[15]将TSTO 助推级和轨道级简化为两个三维楔，基于重叠网格开展马赫数7 条件下层流状态不同轨道级抬升角度的静态与动态数值模拟；获得两级表面压力载荷、流场结构以及三维流动分离拓扑结构，研究分析级间气动干扰对TSTO 气动分离的影响机制。Jia 等[16]针对轨道级为钝头锥 + 圆柱 + 翼构型、助推级为梯形翼的TSTO 模型，通过数值模拟研究了马赫数8.1 条件下不同级间距的级间气动干扰流场，发现激波/边界层干扰导致的壁面压力与热流的跃升随着级间距的增大而减弱。Cheng 等[17]以宽速域飞行器为轨道级，以带翼火箭为助推级，通过数值模拟研究了TSTO 飞行器马赫数6 条件下的热环境。他们分析发现，火箭头部产生的激波入射到轨道级，并在级间产生逐渐减弱的系列反射激波。虽然激波相对温和，没有导致边界层发生分离，但激波作用于壁面还是产生了较高的热流区域；并且随着飞行器攻角的减小，轨道级迎风面的热流呈下降趋势。

已有的研究表明，即使是较为简单的TSTO 外形，级间激波主导的干扰流场也呈现出显著的三维特征。随着TSTO 气动构型的工程化，级间的流动结构和干扰模式变得更为复杂和多样。唐伟等[18]基于建立满足飞行原理、带有共性特征、反映气动特性、适合风洞试验的研究模型的考虑，设计了如图1 所示的背负式TSTO 气动构型方案，旨在为级间干扰和动态分离研究提供研究对象。Peng 等[19]针对唐伟等的TSTO 标模进行缩比和适当简化，在马赫数6 来流条件下开展快响应压敏漆（pressure sensitive paint, PSP）和温敏漆（temperature sensitive paint, TSP）试验，获得不同级间距及攻角条件下激波作用于壁面的干扰区域压力和温度分布。为进一步探索TSTO 标模级间激波/边界层干扰流动机理，本文采用多种试验测量技术以及数值模拟手段，精细刻画典型级间距以及不同流态条件下模型表面及空间的流动特征，揭示TSTO 级间复杂三维激波/边界层干扰流动特性。

图1 TSTO 气动布局方案[18]Fig. 1 TSTO conceptual configuration[18]

1 试验与数值方法

1.1 研究对象

本文将TSTO 标模进行适当的缩比和简化后作为研究对象，如图2 所示。

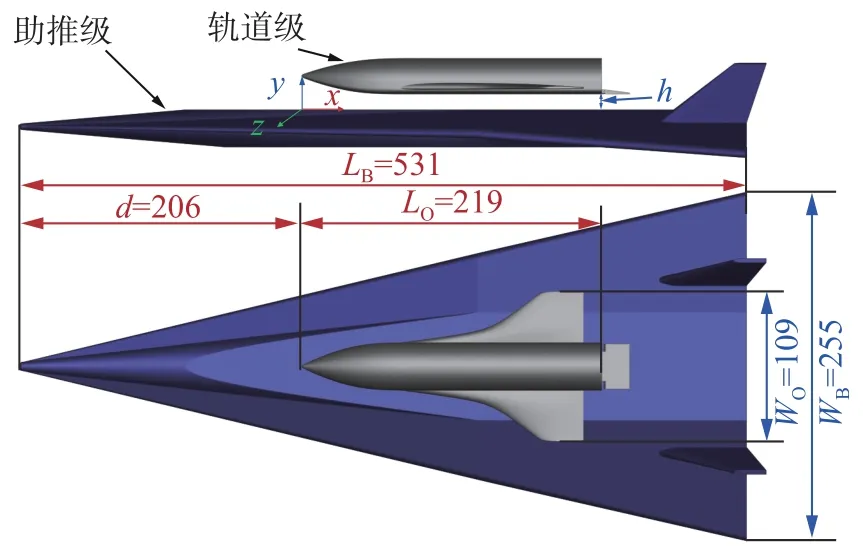
图2 TSTO 模型示意图（单位：mm）Fig. 2 TSTO model configuration (unit: mm)

助推级为椭圆锥导前机身 + 边条后掠翼 + 双垂尾构型，上壁面削平形成的突起平台用于安放轨道级，轨道级为翼身组合体。本研究重点关注助推级与轨道级之间的干扰流场，因此将助推级机身下壁面简化为了平面，机翼简化后去掉下折的机翼翼梢，去掉轨道级上部垂尾。根据风洞对模型尺寸的约束，模型几何缩比为1∶160，助推级模型总长LB=531 mm，翼展WB=255 mm；轨道级模型总长LO=219 mm，翼展宽度WO=109 mm；轨道级与助推级呈上下并联布置，水平方向上轨道级头部固定在助推级前缘下游d=206 mm处。助推级上壁面与轨道级下壁面之间的距离定义为级间距h。坐标系固定于助推级上壁面，以轨道级头部顶点在助推级上的投影为原点，x轴与来流方向一致，y轴垂直助推级上壁面并向上，z轴满足右手定则。为便于不同尺度模型之间的对比与关联，模型坐标值及级间距均以轨道级长度LO作为参考长度进行无量纲化。

1.2 试验设备与来流条件

风洞试验在中国空气动力研究与发展中心超高速所Φ0.5 m 高超声速风洞中开展。该风洞是一座暂冲吹吸式常规高超声速风洞，单次风洞的有效试验时间可超过30 s，总压和总温控制精度优于1%。试验来流马赫数Ma=6，总压p0=1 890 kPa，总温T0=492 K。 表1 给出了自由来流的具体参数，其中p∞、T∞和Rel分别表示来流静压、静温以及单位雷诺数。

表1 自由来流条件Table 1 Freestream conditions

1.3 试验方法

试验时，助推级模型采用具有法向间距调节能力的腹部支撑，轨道级模型采用尾支撑；两级模型攻角和侧滑角均为0°；两级模型的无量纲级间距分别为h/LO=0.023、0.051和0.123，其中级间距h/LO=0.023条件下的流动为分离初始产生的缝隙流，h/LO=0.051条件下的流动为级间具有多次激波反射的典型小通道流动，而h/LO=0.123条件下的流动为随着分离距离增大级间激波反射已减少至1 次时的末期小通道流动。

试验通过纹影和纳米示踪的平面激光散射（nano-tracer-based planar laser scattering, NPLS）非接触测量技术显示模型级间激波/边界层干扰流场结构，荧光油流用于获取助推级上表面流谱，在级间上下壁面沿流向布置静压测点以获取不同级间距的压力信息。

纹影光路呈“Z”形布置，观察窗口直径为500 mm，纹影相机分辨率为2048 × 2048，采样速率为25 帧/s。NPLS 测量通过在流场中注入二氧化碳气体，在经过喷管膨胀时凝结成干冰微团作为示踪粒子；厚度小于1 mm 的脉冲激光片光照射模型中心平面流场，分辨率为2048 × 2048 的CCD 相机采集干冰产生的瑞利散射瞬时图像。油流测量需要在试验前将混合荧光粉的硅油均匀喷涂到模型表面，试验过程中通过在风洞试验段上方布置高速摄影仪获取荧光油流流动图谱，图像分辨率为1920 × 1080，采样速率为69 帧/s。

试验通过DTC initium 电子扫描压力测量系统测量级间壁面静压，其中在助推级上壁面中心线x/LO=0.11～1.21范围内均布13 个静压测点，在展向z/LO=0.046处x/LO=0.47～1.21范围内均布5 个测点；在轨道级下壁面中心线x/LO=0.27～0.84范围内均布13 个静压测点，在展向z/LO=0.027处x/LO=0.27～0.89范围内均布10 个测点。所有测点通过管道连接到上量程为69 kPa 的扫描模块上，综合测量精度优于±0.1% FS。

1.4 数值模拟方法

定常数值模拟用于获取更多的级间空间流场信息。不考虑侧滑情况，选取半模进行计算。计算采用中国空气动力研究与发展中心自主研发的非结构计算流体力学软件NNW-FlowStar[20]。该求解器基于二阶非结构混合网格的格心型有限体积方法。选择HLLE + + 格式和Venkatakrishnan 限制器，保证空间为二阶精度；分别采用层流和k-ωSST 湍流模型进行黏性模拟，用以对比不同黏性模式对模拟结果的影响。边界条件使用无反射的超声速压力远场和对称面边界，壁面采用等温壁条件（Tw=300 K）；计算的自由来流条件与试验保持一致（详见表1）。

计算流场空间采用四面体非结构网格，近壁区域采用加密四面体棱柱网格，以期更为精确地刻画近壁区域的流场细节。为提高级间复杂反射波系结构及激波/边界层干扰引起的流动分离区域的分辨率，本文特使用了NNW-FlowStar 软件内置的网格自适应模块[21]。针对级间复杂流动特征结构，本文采用激波判别法（特征线判别[22]）用于识别和标记目标特征。针对目标网格分布，本文采用“H”形（剖分式）自适应技术对网格进行优化（如图3 所示）。

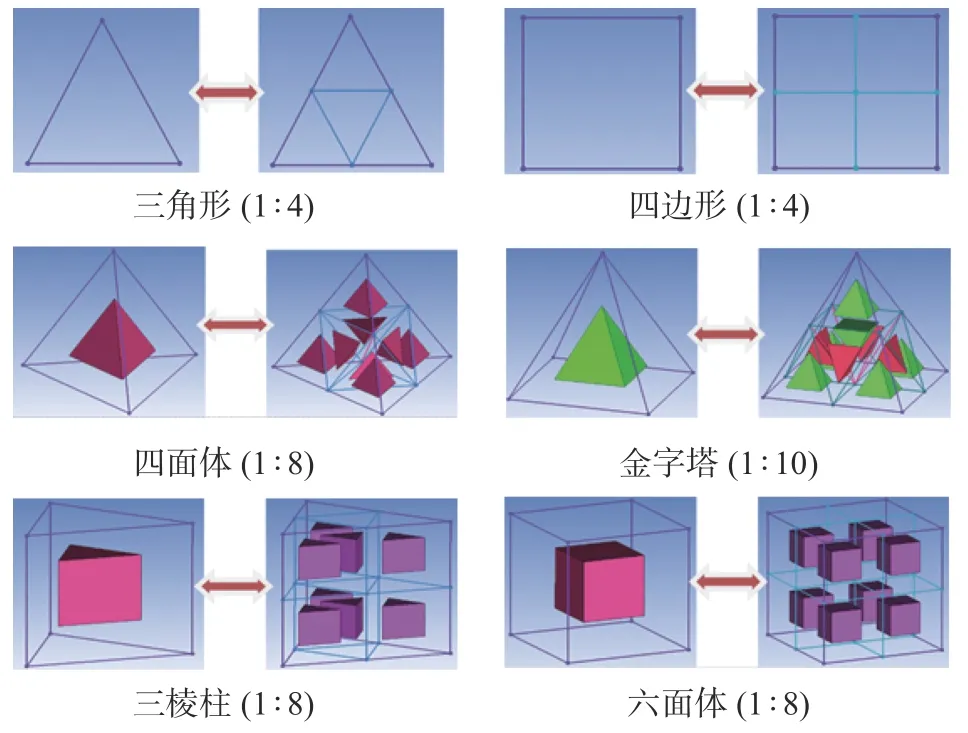
图3 网格自适应加密方式[21]Fig. 3 Adaptive mesh refinement approaches[21]

图4 对比了有、无网格自适应加密条件下，级间距h/LO=0.051的层流计算结果，分别给出了马赫数云图、压力系数云图为自由来流动压）及模型表面与对称面网格示意图。如图4（a）所示，无网格自适应加密得到的激波波面不够锐利，级间流场也不够细致。而使用网格自适应模块后，网格量由600 万左右增加至2300 万左右，网格沿着激波所在的区域加密，使得激波和流场的模拟更为精细，结果如图4（b）所示。

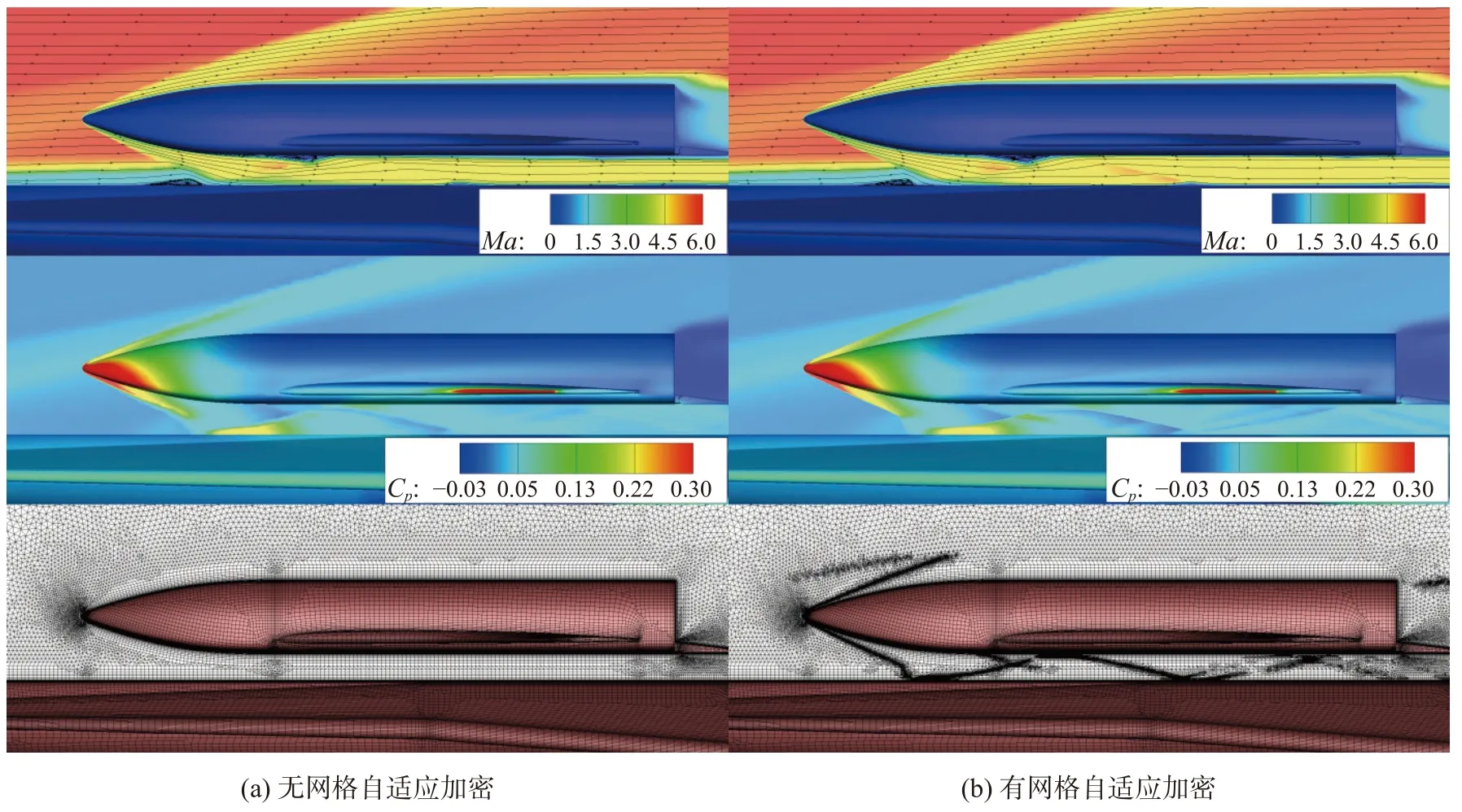
图4 有、无自适应网格加密的层流计算流场Fig. 4 Laminar flow field with/without adaptive mesh refinement

2 结果及讨论

2.1 壁面边界层流态

图5 给出了h/LO=0.023、0.051、0.123三个典型级间距下的NPLS 图像。

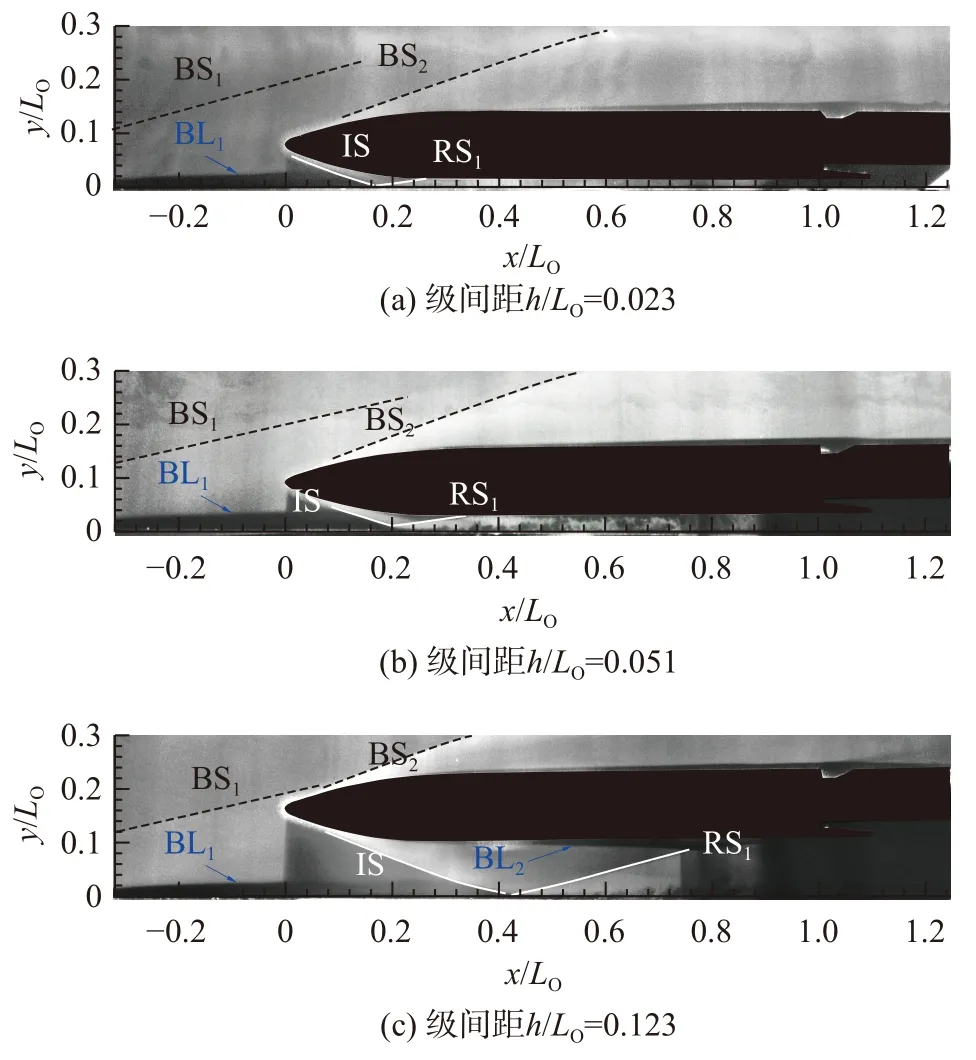
图5 典型级间距条件下的NPLS 图像Fig. 5 NPLS of flow fields within typical stage clearances

在激波入射之前，助推级和轨道级的壁面边界层（BL1和BL2）均处于层流状态。当激波IS 入射到助推级上壁面层流边界层时，流动分离发生，同时分离泡以及剪切层引起的流动不稳定性使得反射激波RS1下游的再附边界层迅速转捩为湍流状态[23-25]。对于小级间距h/LO=0.023的情况，助推级上壁面x/LO=0处（轨道级头部顶点的垂直下方）的层流边界层厚度yδ/LO≈0.038（u/ue=0.99处，如图6 所示），大于级间间隙高度，级间处于边界层内的低动量流动状态，甚至可能发生“雍塞”的情况，因此在NPLS图像中级间没有呈现显著的流动结构。对于级间距h/LO=0.051，反射激波RS1同样导致了轨道级下壁面边界层迅速转捩为湍流。而对于级间距h/LO=0.123，RS1入射点靠近轨道级模型尾部，干扰后的边界层不在激光照射区域内，并且在激波强度不够的条件下有可能发生边界层在激波入射后仍然保持层流的情况[24]，因此无法判断RS1激波作用之后的边界层流态。

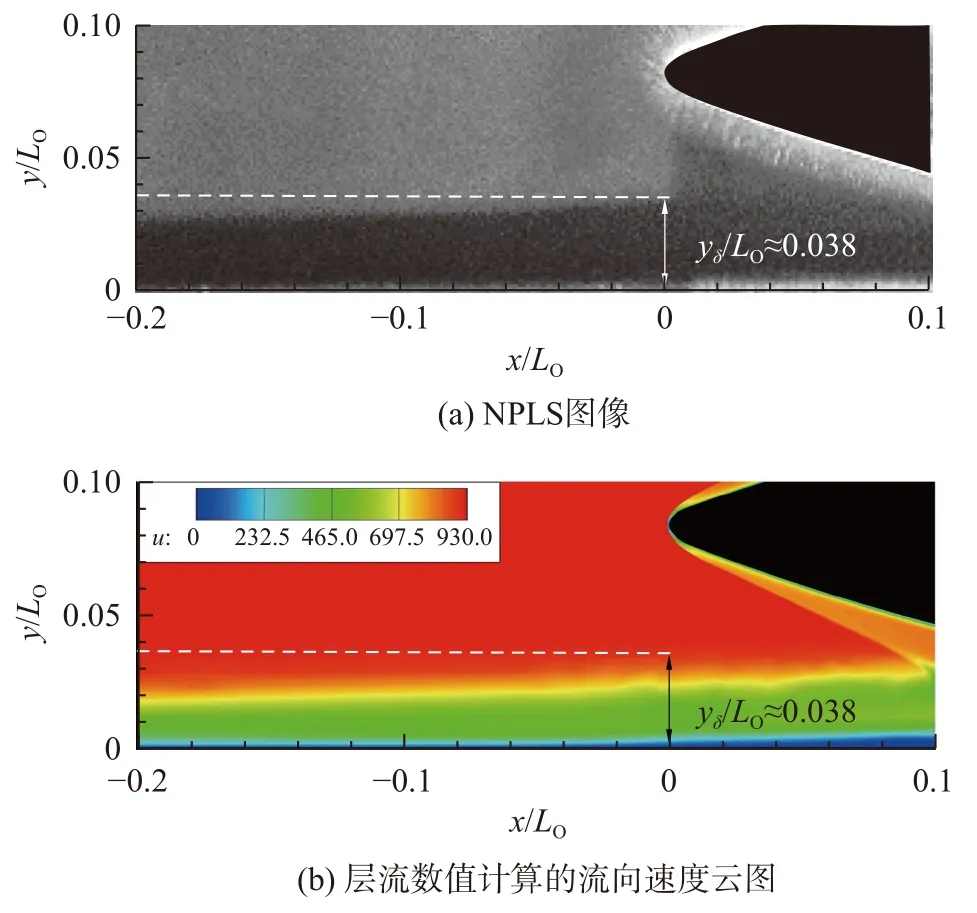
图6 助推级上壁面x/LO = 0 处边界层厚度Fig. 6 Boundary layer thickness over the upper booster wall at x/LO = 0

鉴于级间距h/LO=0.051的级间流场具有典型的激波/边界层三维多波系复杂干扰结构特征，本文针对该级间距进行了详细的流动特性分析。

2.2 级间波系结构

图7 给出了级间距h/LO=0.051的试验纹影与数值模拟的对称面密度梯度云图，以虚线标示出激波的形状。助推级头部产生的弱斜激波为BS1；轨道级头部产生的激波分别为BS2以及IS，IS 作用于助推级上壁面导致边界层流动分离，并形成反射激波RS1。由于层流边界层抵抗逆压梯度的能力较弱，RS1作用到轨道级下壁面层流边界层时形成大尺度的流动分离，产生较强的分离激波SS1（红色虚线标示），其作用于助推级上壁面后还能形成反射激波SS2（见图7（b））；同时，RS1在轨道级下壁面形成的反射激波RS2作用于助推级层流边界层时同样产生分离激波SS3和反射激波RS3，并最终在轨道级尾部产生系列压缩波系。而对于湍流状态（见图7（c）），RS1在轨道级下壁面形成的流动分离尺度较小，产生的分离激波SS1强度较弱，同时RS1在级间壁面来回反射，依次形成反射激波RS2、RS3以及RS4，在这些激波入射位置未见明显的流动分离结构。

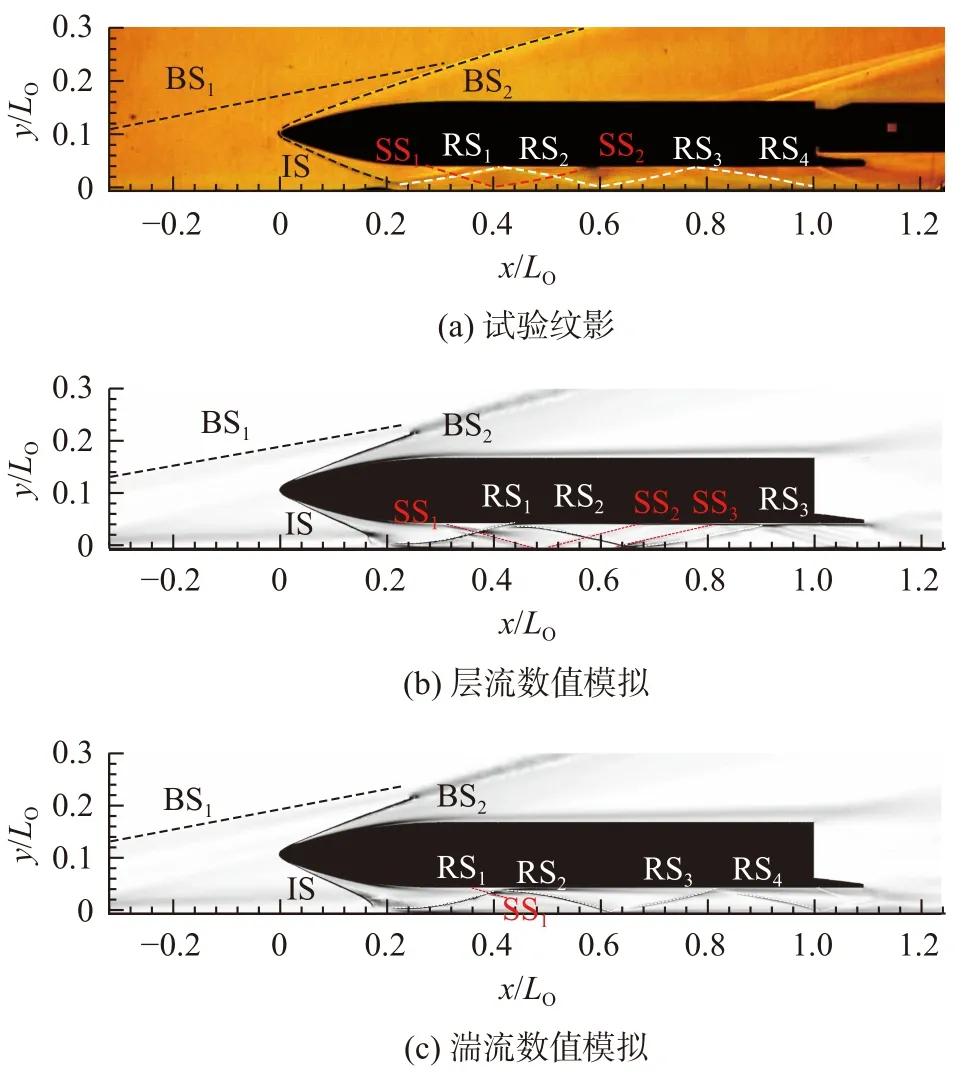
图7 试验纹影与计算密度梯度图Fig. 7 Schlieren result and computed density gradient

图8 给出了助推级和轨道级相对壁面中心线及展向特定位置的试验与计算的流向压力系数分布。在激波IS 入射前，助推级上壁面先后经历压缩与膨胀后，中心线壁面压力已下降到接近于来流静压的平稳状态。当入射激波IS 作用于壁面边界层后，流动分离与再附发生，在中心线x/LO=0.276处引起最大压力跃升（位于反射激波RS1起始点下游），对应的层流和湍流压力系数分别达到0.252 和0.234。而轨道级由于头部下壁面凸曲面构型产生的膨胀波的影响，壁面压力持续下降，反射激波RS1入射轨道级下壁面边界层，并在其中心线x/LO=0.471壁面处引起最大压力跃升，对应的层流和湍流压力系数分别是0.118 和0.117。随后产生的反射激波强度逐渐减弱，引起的压力跃升也逐渐减小。值得注意的是，由于层流边界层更易发生流动分离，其分离起始点较湍流状态更靠近上游，导致层流边界层受到激波IS 和RS1作用引起的压力跃升起始点更靠前。特定展向位置的流向压力变化趋势与中心线基本一致，但具体的压力系数值以及波系结构位置存在一定的差异，呈现出干扰的三维特征。此外，由于试验中模型壁面边界层在激波干扰之前为层流状态，干扰后迅速转捩为湍流状态（见图5（b）），因此试验纹影及压力测量结果在第一道激波（IS 或者RS1）的作用结束之前与层流计算结果一致，而在激波作用之后，与湍流计算结果吻合。

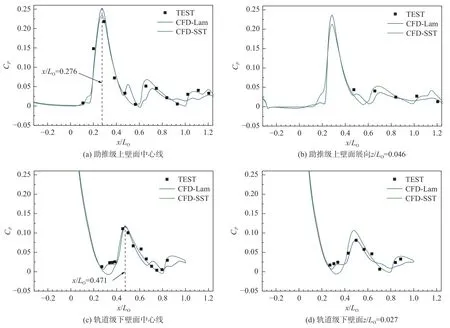
图8 模型壁面的流向压力分布Fig. 8 Streamwise variations of the wall pressure coefficients

2.3 壁面流动图谱

图9 （a）和图9（b）分别给出了荧光油流试验获得的模型壁面流动图谱和计算得到的壁面极限流线图。试验中，在入射激波IS 的作用下，助推级上壁面位于轨道级头部下方两侧的肩部出现了对称的旋涡结构，同时发现了旋涡下游沿流向方向的分离线；而位于轨道级垂直下方的干扰区因被遮挡，所以未能显示。由于激波RS1的作用，轨道级下壁面x/LO=0.24附近靠近中心线区域出现了弧形的分离线，并且在分离线的两端形成一对旋涡。通过对比试验与计算的流线图谱可以看出，层流计算结果在相应区域出现与试验非常类似的流动结构，包括流动分离线与旋涡结构；而湍流计算结果与试验存在较大的差异。这进一步说明在助推级上壁面和轨道级下壁面各自第一道激波干扰结束前的试验流场更接近于层流状态。

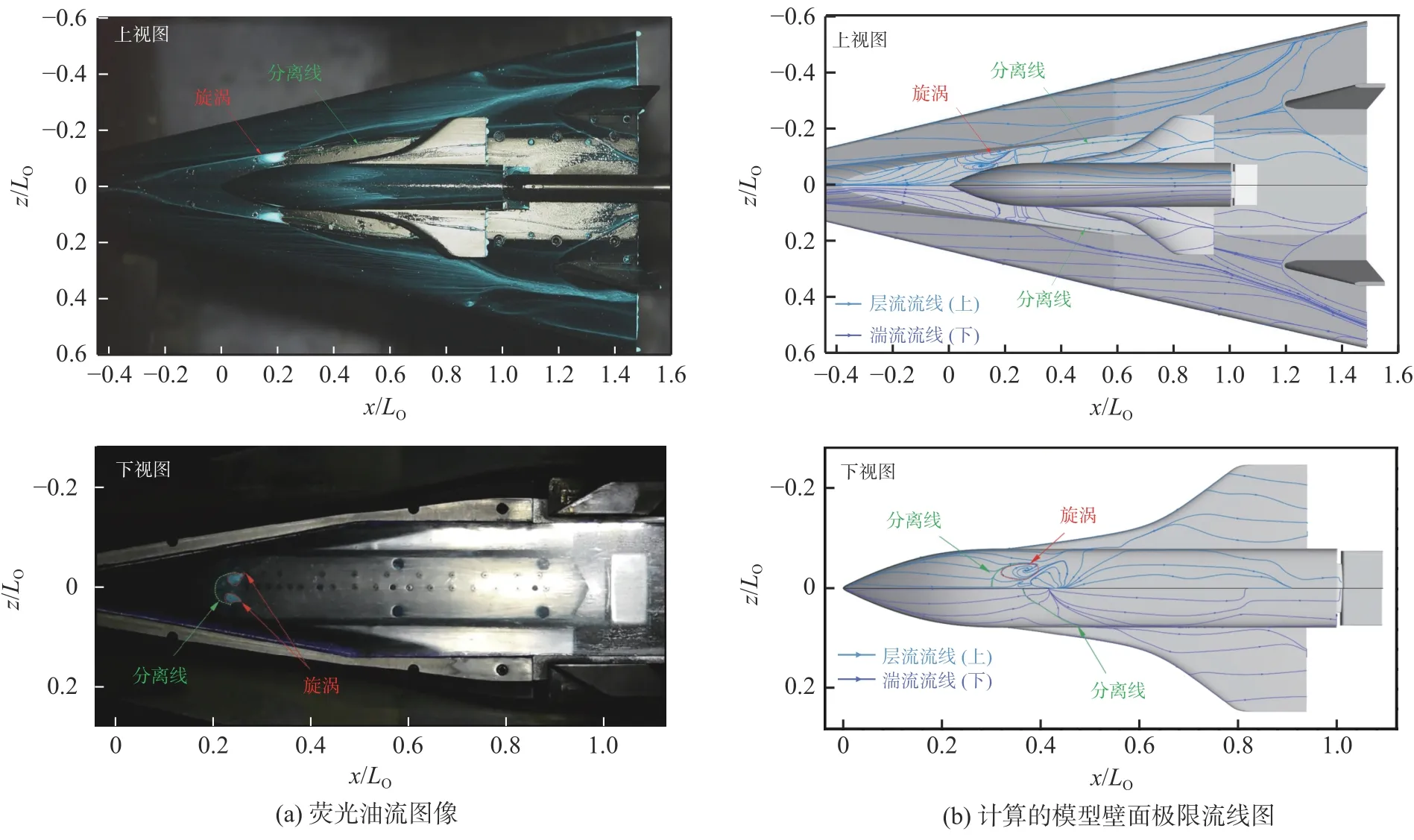
图9 模型壁面流动图谱Fig. 9 Flow topology at the wall

图10（a）给出了激波IS 作用下的助推级上壁面干扰区局部放大图。图中层流和湍流结果以上下对称方式给出，同时给出了壁面的压力系数和壁面极限流线；用白色和蓝色虚线分别刻画分离线和再附线位置，并标示出干扰流场中的鞍点S、结点N 和焦点F，下标“b”表示位于助推级，上标“*”代表湍流结果。图10（b）则给出了干扰区壁面中心线最大压力系数处（x/LO=0.276，在图10（a）用黑色虚线标示）横截面的压力系数云图。结合壁面极限流线与压力系数云图可以看出，激波IS 引起的干扰区呈现显著的三维特征。轨道级头部产生的三维激波在周向空间上呈环状分布（IS），在其入射助推级上壁面导致流动分离的同时，也形成了反射激波RS1和整体呈弧状向下游展开的高压区。在x/LO=0.276的横截面处，反射激波RS1的波面在展向逐渐靠近助推级壁面，形成位于高压区内中心线以及展向z/LO=0.04附近的两个压力峰值，层流状态的展向压力变化特征更为明显。此外，壁面分离流动是开放的，即分离区的流线不再都起于分离线、止于再附线，干扰区内出现鞍点、结点、焦点等临界点结构[26]，并且层流状态的干扰流场区域要明显大于湍流状态，流场结构也更为复杂。

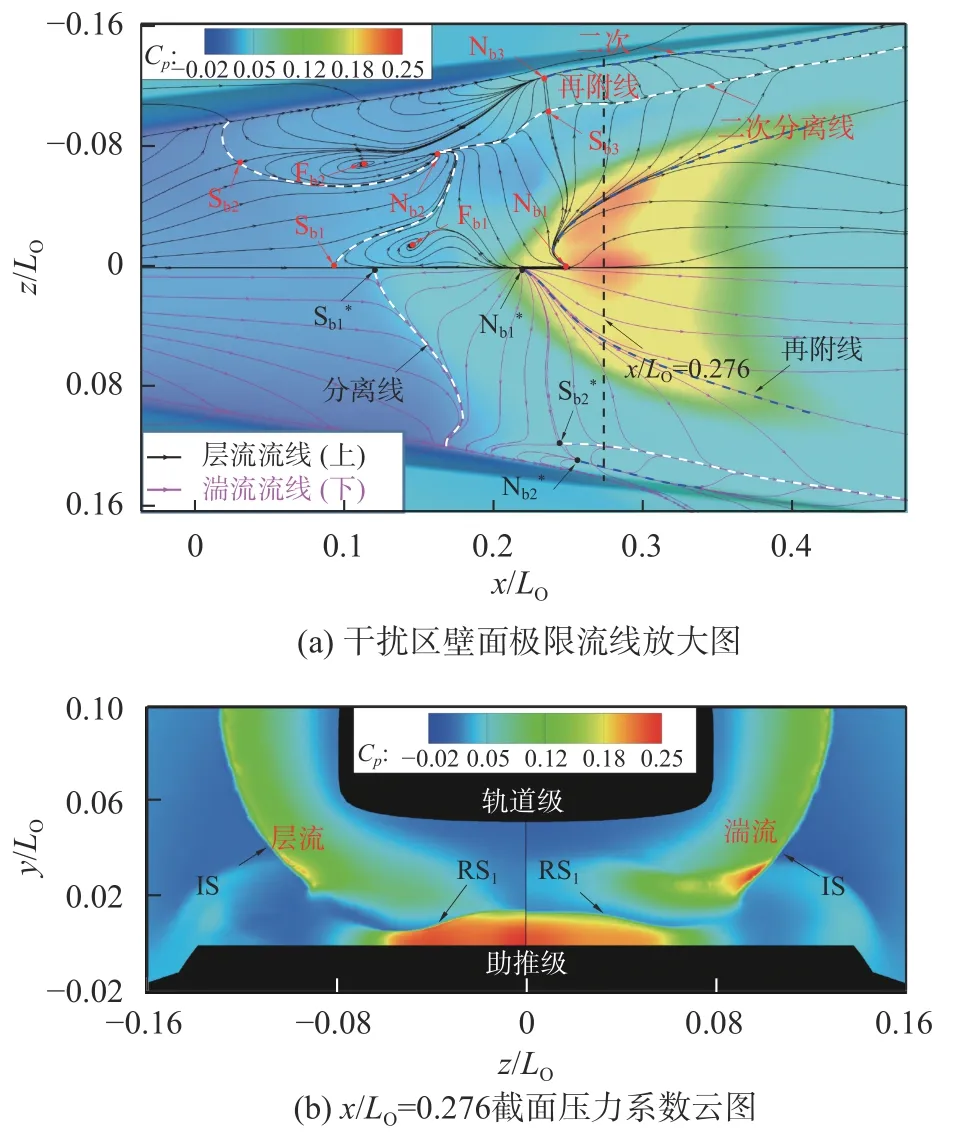
图10 激波IS 入射助推级上壁面形成的干扰区流场Fig. 10 Flow fields induced by the impingement of shock wave IS on the upper booster wall

首先，由于层流边界层抵抗逆压梯度的能力较弱，在强的入射激波IS 作用下，大尺度流动分离产生，形成中心线上x/LO=0.092处的分离鞍点Sb1和x/LO=0.248处的再附结点Nb1。其次，由于激波IS 的三维特性，高压区在展向向下游移动且压力值逐渐降低，致使分离线在展向快速弯曲；同时来流沿分离线的流动偏转及分离区内的逆向流动共同作用，导致了顺时针螺旋围绕焦点Fb1的“龙卷风”旋涡结构（tornado-like vortex[26]）形成。另外，在靠近助推级凸起平台的边缘处，平台下方气流进入平台时发生卷曲，形成了顺时针旋转的源于结点Nb3的涡结构；该旋涡与来流相向运动产生的剪切作用产生了焦点为Fb2的逆时针旋转“龙卷风”旋涡结构，相邻的两个旋涡将分离线推向上游并以两者之间的鞍点Sb2-结点Nb3连线为渐进收敛边界；中心区域与边缘的分离线在结点Nb2处交汇并发生转折；而源于结点Nb1的再附线在展向向下游延伸，与高压区轮廓相似。此外，平台外侧产生的压缩波（如图10（b）所示）在平台边缘形成展向逆压梯度，进而引起展向的流动分离，形成流经结点Nb2和鞍点Sb3的沿流向方向的二次分离线，以及源于结点Nb3的二次再附线。而湍流干扰流场则相对简单，湍流边界层抵抗逆压梯度能力较强，中心线上的分离鞍点Sb1*和再附结点Nb1*相对层流状态向内收缩，分别位于x/LO=0.121和x/LO=0.219处；同样的，在助推级凸起平台的边缘处也有因下方气流上洗带来的旋涡以及展向压力梯度引起的二次流动分离，但是尺度都相对较小；沿流向方向的二次分离线与再附线分别流经鞍点Sb2*和结点Nb2*。由于湍流分离区尺度较小，来流与分离区逆向流动之间的剪切较弱，没有形成焦点以及“龙卷风”旋涡结构。

图11（a）给出了轨道级在反射激波RS1作用下的干扰区壁面流场。图中鞍点S、结点N 和焦点F 的下标“o”表示位于轨道级上；同样的，上标“*”代表湍流结果。图11（b）则显示了干扰区壁面中心线最大压力系数处（x/LO=0.471，在图11（a）用黑色虚线标示）横截面的压力系数云图。反射激波RS1入射轨道级下壁面引起的高压区也呈弧状向下游展开；在x/LO=0.471截面可以看到未作用到轨道级壁面、向空间发展的激波RS1以及在轨道级壁面反射形成的激波RS2；激波RS2波面在展向也逐渐靠近壁面，并且强度呈递减趋势，层流状态压力系数在展向的下降速率要高于湍流状态，进而导致高压区在展向持续距离较短。

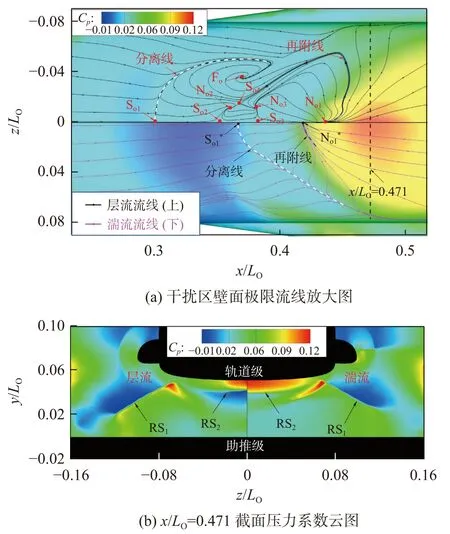
图11 激波RS1 入射轨道级下壁面形成的干扰区流场Fig. 11 Flow fields induced by the impingement of shock wave IS1 on the lower orbiter wall

轨道级壁面边界层受激波RS1作用引起的分离区明显也是开放的，层流状态的干扰流场也相对复杂且范围较大。中心线上的分离鞍点So1和再附结点No1分别位于x/LO=0.300和x/LO=0.430处。在轨道级边缘与分离区内，带展向方向的相对流动导致了展向分离线的弯曲以及焦点位于Fo处的“龙卷风”旋涡的产生，进而在分离区内形成位于中心线的鞍点So2和So3，以及展向并列的结点No2和No3。随后，源于结点No1、No2、No3的流线在鞍点So4处渐进收敛，进而将中心分离区划分为三个部分；在鞍点So2-So4和结点No2-No3围成的区域内，产生向下游的流动，方向与其余两部分分离区相反。而对于湍流状态，流动分离起始点大幅后移，分离区的流动结构也相对简单，只有中心线上的分离鞍点So1*和再附结点No1*分别位于x/LO=0.366和x/LO=0.418处，以及经过两点并在展向发生弯曲的分离线和再附线，没有出现其他的鞍点、结点以及焦点等临界点。

图12 给出了RS1下游其余反射激波（RS2~RS4）作用在助推级和轨道级壁面的极限流线图，并用黑色虚线标示出图7 所示激波引起的壁面中心线压力峰值的位置，在未发生流动分离时可认为是激波入射点。

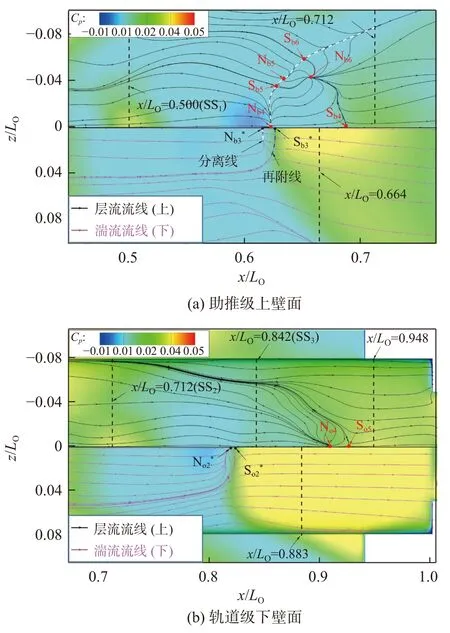
图12 激波RS1 下游壁面流场Fig. 12 Flow structures downstream of shock wave RS1

随着激波在级间的来回反射，激波/边界层干扰强度依次递减。对于助推级，激波SS1没有引起层流边界层发生分离，而激波RS2则导致层流和湍流状态均发生流动分离。其中，层流状态中心线分离结点Nb4和再附鞍点Sb4分别位于x/LO=0.622和x/LO=0.687处，由Nb4发展的分离线呈弯曲状，依次经过鞍点Sb5、结点Nb5以及鞍点Sb6，而再附线则终止于结点Nb6处。此时，激波RS2在助推级壁面产生的干扰强度和范围均远小于激波IS 的作用，其中心线分离区长度只有后者的42%左右。湍流状态的分离区中心线起始位置分别位于结点Nb3*（x/LO=0.615）和鞍点Sb3*（x/LO=0.626）处，并且在展向的持续距离也很短，流动分离带来的影响较弱。相应地，激波SS2和SS3也没有引起轨道级层流边界层发生分离，而激波RS3产生的层流和湍流状态的流动分离尺度都很小，特别是湍流状态，分离结点N02*（x/LO=0.819）和鞍点S02*（x/LO=0.823）非常接近，分离对流动带来的影响非常弱。

2.4 空间流动特征

图13 给出了激波IS 干扰区的级间空间流场结构及流线，其中对称面和x/LO=0.276横截面展示马赫数云图，模型壁面展示压力梯度。

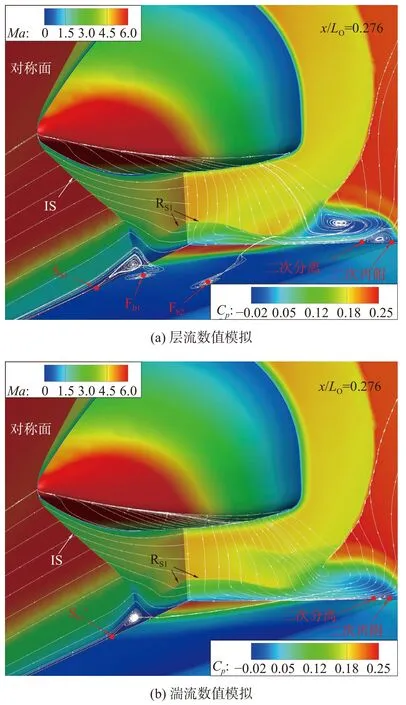
图13 激波IS 作用干扰区的空间流场Fig. 13 Three-dimensional flow fields in the interference area induced by the impingement of shock wave IS

从对称面分离泡向展向空间发展的流线可以看出，分离泡在空间上也不再是封闭形式。其中，层流对称面分离泡内有流向相邻焦点Fb1的气流，因此该处的“龙卷风”旋涡流动方向是从空间螺旋卷向壁面；而源于焦点Fb2的空间流线则是由壁面螺旋上升并随主流向下游流动。另外，湍流对称面分离泡内向展向逃逸的气流则直接随主流向下游流动。助推级近壁区域的横向流动在平台边缘处受到逆压梯度的影响，发生流动分离；明显地，层流状态的这种二次分离尺度要大于湍流状态，并且层流较大的流动分离还导致其上方产生空间旋涡结构。

图14 给出了激波RS1干扰区的级间空间流场结构及流线，选择x/LO=0.471处横截面展示横向流动。由于层流的分离区较大，导致对称面上的分离激波SS1以及与RS1之间的干扰都明显强于湍流状态；同时，层流对称面的分离区内存在对应于壁面鞍点So2和So3的两个旋转中心；壁面焦点Fo汇聚有包括来流、对称面分离区靠近上游的旋转中心以及再附结点的空间流线，并且呈螺旋状流向壁面；湍流对称面分离区内也有横向流出并随主流向下游传播的气流。另外，在x/LO=0.471横截面，轨道级近壁区域气流也由于展向的顺压梯度产生横向流动，但没有在展向形成流动分离。

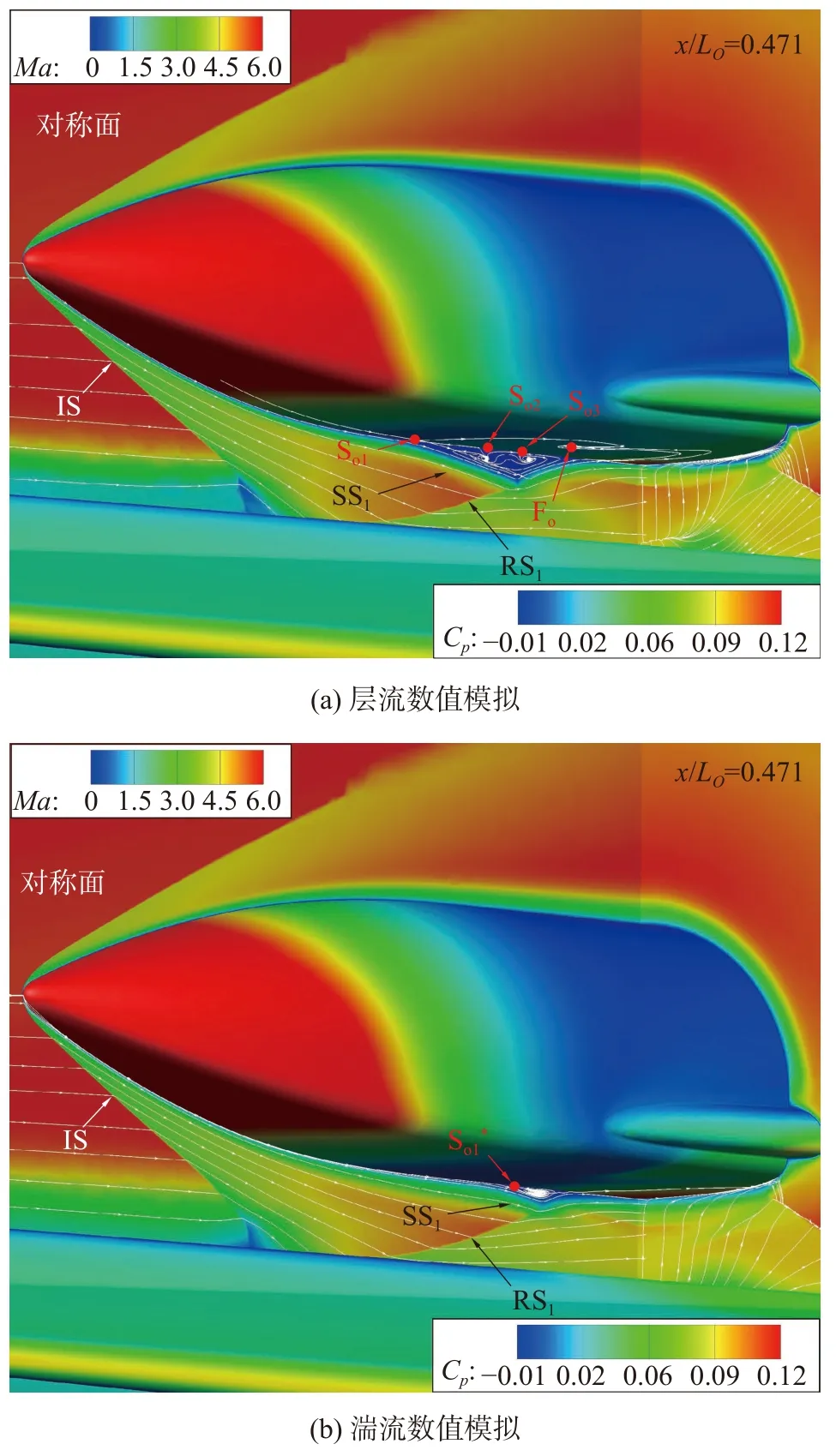
图14 激波RS1 作用干扰区的空间流场Fig. 14 Three-dimensional flow fields in the interference area induced by the impingement of shock wave RS1

3 结 论

针对TSTO 标模缩比模型，通过纹影、NPLS、壁面静压测量以及油流图像等多种试验技术，结合层流与湍流的数值模拟手段，获取了马赫数6 条件下的助推级与轨道级典型级间激波/边界层干扰流场流动图谱与压力分布，并展示了壁面干扰结构与空间流场之间的相关性。通过分析得到以下结论：

1）试验中，助推级与轨道级模型壁面边界层在激波入射之前均保持为层流状态，激波引起层流边界层分离的同时增强了流动的不稳定性，导致强干扰后的再附边界层迅速转捩为湍流状态，因此试验结果在第一道激波的作用结束之前与层流计算结果吻合，而在激波作用之后，与湍流计算结果一致。

2）激波/边界层干扰呈现复杂的三维流动特征，轨道级头部贴体激波入射至助推级上壁面形成的高压区呈弧状向下游展开，随后激波在级间来回反射并且激波/边界层干扰强度依次递减；同时，干扰区内存在显著的横向流动，主分离线与再附线也在展向发生弯曲变形；分离区不再是起止于分离线和再附线的封闭结构，而是向空间发展并随主流向下游传播，伴随上游气流从侧向汇入，分离区呈明显的开放结构。此外，展向的压力梯度导致在助推级上壁面平台边缘处发生流动分离，形成沿流向排列的二次分离线与再附线。

3）由于层流边界层抵抗逆压梯度的能力较弱，其受到相同激波作用形成的干扰区明显大于湍流状态，同时流动结构更为复杂，开放特征也更为显著。在强干扰区内壁面上存在包括鞍点、结点、焦点在内的临界点以及有旋涡结构的流动特征；且源于焦点的“龙卷风”旋涡，其流动方向既可能从壁面螺旋上升，也可能从空间螺旋卷向壁面。

4）对于TSTO 标模级间三维激波/边界层干扰引起的大尺度流动分离与旋涡结构，其非定常特性将是级间可控分离所关注的另一焦点问题，后续将开展深入研究。

致谢：感谢中国航天空气动力技术研究院沈清、陈兰、胡静等在TSTO 标模多体分离特性研究中的支持，感谢中国科学技术大学李祝飞关于本文研究内容的有益讨论。