基于新型趋近律的板球系统反步滑模最优控制
徐 鹏,向凤红,李江峰
(昆明理工大学 信息工程与自动化学院,云南 昆明 650500)
板球系统由于其自身的强耦合性、参数不确定性以及多变量等特性,常被用于检验各种控制算法的实验平台.针对板球系统存在的问题,国内外学者进行了大量的研究.Sergio 等[1]通过建立板球系统完整的非线性模型,提出一种带非线性补偿的渐进稳定双比例微分(Proportional Derivative,PD)控制策略,实验结果表明,所设计的控制器具有良好的性能.Kan 等[2]利用最小相位输出对非简化非线性模型设计跟踪控制器,仿真实验表明其跟踪误差指数收敛到零,验证了所设计控制器的有效性.由于板球系统存在摩擦力,难以实现高精度控制,王永坤等[3]提出一种基于降阶观测器的线性控制器,实现了在既不需要精确的摩擦模型,也不需要估计具体特征参数的环境下对板球系统轨迹跟踪控制,且具有良好的动态品质.为了实现板球系统高精度轨迹跟踪,韩光信等[4]通过目标状态建立偏差系统,并结合预测控制中的滚动优化思想设计了滚动线性二次型控制器,所设计的控制器同样具有良好的轨迹跟踪性能和鲁棒性能.此外,Backstepping 控制[5]、滑模变结构控制[6]、切换控制[7]与自适应控制策略[8]等方法在板球系统也得到了广泛应用,相比传统比例积分微分(Proportional Integral Derivative,PID)控制,无论是动态性能还是稳态性能都有显著提升.
反步法(Backstepping)设计的基本原理是将复杂的非线性系统拆解为不超过系统阶数的子系统,并为每个子系统分别设计Lyapunov 函数与虚拟控制量,从后往前进行反向推导,直至完成系统的控制器设计.但传统的反步法控制无法保证系统鲁棒性,且容易出现微分爆炸现象.文献[9]采用级联严格反馈形式,分别用线性扩展状态观测器和跟踪微分器估计模型的不确定性和虚拟控制的导数,避免了微分爆炸现象的发生,设计了观测器集成反步法控制,提升了系统的跟踪性能,但稳态性能有所欠缺.文献[10]为了削弱对数学模型的依赖,同时防止微分爆炸现象的发生,引入动态面策略,提出了一种反演自适应动态换模控制方法,提升了系统动态跟踪性能,但其响应速度较慢.文献[11]将Backstepping 方法与H∞控制理论相结合,提出一种自适应神经网络H∞控制策略,改善了系统抗干扰能力,但其轨迹跟踪精度仍然较低.文献[12]为了改善系统抗干扰能力,采用全程快速微分器对带有噪声干扰的输入信号进行滤波处理,并基于反步法设计了非线性反馈控制器,有效提高了轨迹跟踪精度,但其响应速度较慢.
滑模变结构控制本质上是使系统按照预定“滑动模态”的状态轨迹运动的一类特殊非线性控制,最大的优点是对系统干扰与参数摄动具有完全自适应,但最突出的问题就是抖振.文献[13]为了提高系统动态响应与稳态跟踪精度,提出了变指数幂趋近律,并且将积分终端滑模面与互补终端滑模面相结合的策略,设计了一种基于滑模控制的非线性算法,通过实验验证了该策略的有效性,但抖振抑制效果不显著.文献[14]提出了一种级联分数阶滑模控制器,改善了板球系统的响应速度,抑制了系统抖振,但跟踪精度有所欠缺.文献[15]将监督模糊控制与滑模控制相结合的控制方法,提高了小球轨迹跟踪的精度,但抗干扰性较弱.李江峰等[16-17]先后提出了一种基于新型幂趋近律的滑动区域法滑模控制策略与基于遗传算法优化的组合趋近律滑模控制,提高了轨迹跟踪精度,但均未解决惯性所带来的扰动.
针对上述存在的问题,本文将反步法与滑模控制相结合,提出一种基于新型趋近律的反步滑模最优控制策略.在反演过程中,首先,通过轨迹跟踪误差构造Lyapunov 函数,由此设计中间虚拟控制量;其次,通过轨迹跟踪误差与虚拟控制量设计动态滑模面,以增强系统鲁棒性;然后,在系统满足Lyapunov全局稳定的前提下,设计一种新型趋近律,以提高系统收敛速度,同时保证系统抑制抖振的效果,并由此设计系统控制器;最后,引入粒子群算法寻找一组新型趋近律的最优参数,为防止算法陷入局部最优解.本文将迭代次数分成前期中期与后期,分别赋予不同的速度惯性权重、自我学习因子与群体学习因子,以提高寻优收敛精度与效率.通过仿真实验验证了所设计控制策略的可行性与有效性.
1 板球系统建模
选取固高GBP2001 为本文研究实验平台,如图1 所示.板球系统主要由小球、球盘、伺服电机、控制器、摄像头、连杆机械系统与直流电源等构成.

图1 GBP2001 板球系统实物模型Fig.1 The physical model of the GBP2001 ball and plate system
由于板球系统为典型的多输入多输出非线性系统,很难建立精确的数学模型,故本文在不影响系统性能的前提下,作出以下假设:①小球与板面无摩擦力干扰;②小球与板面未发生脱离;③系统内部机械结构之间无摩擦损耗;④球盘对小球无界限约束.
选取板面中心为小球位置原点(0,0).板面x轴方向对地倾角为α1,y轴方向的倾角为α2,其动力学分析如图2、3 所示[18].
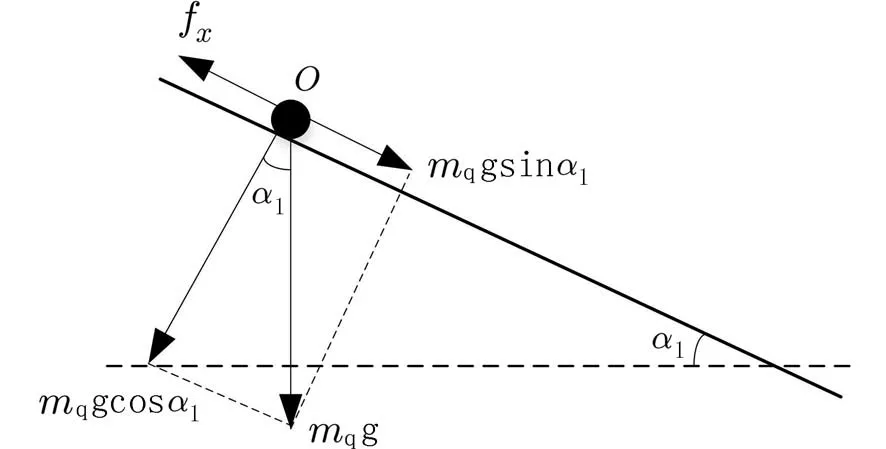
图2 系统x 轴物理模型Fig.2 The physical model of system x-axis

图3 系统y 轴物理模型Fig.3 The physical model of system y-axis
由拉格朗日方程得到板球系统的微分方程组如式(1)所示,式中各参数意义如表1 所示[19].

表1 板球系统动力学方程参数Tab.1 Parameters of dynamics equation of the ball and plate system
当小球在稳定工作点附近时,其倾角很小,且两个伺服电机也是固定的,故可作以下近似处理[16]:
由式(1)~(4),得到板球系统线性化数学模型:
由式(5)知,系统x轴方向与y轴方向对称,故本文只分析x轴方向子系统,y轴方向子系统原理相同,不再赘述.
选取平板对地倾角α1作为子系统输入量ux,小球x轴方向所在位置与速度作为系统状态x1与x2,得到x轴子系统的状态空间方程:
为检验系统的鲁棒性,引入干扰项d(t),|d(t)|≤D,D为常数.令 g(x)=-γg,整理式(6)得:
2 基于新型趋近律的反步滑模控制器设计
反步法其本质是将复杂的非线性系统拆解为不超过系统阶数的子系统,并为每个子系统分别设计Lyapunov 函数与虚拟控制量,从后往前进行反向推导,直至完成系统的控制器设计.但传统的反步法控制无法保证系统鲁棒性,且容易出现微分爆炸现象,为解决这一问题,本文通过引入滑模项,克服系统干扰,增强系统鲁棒性,同时规避微分爆炸现象的发生.但滑模项的引入,会给系统带来高频抖振的弊端.为达到加快系统响应速度、控制精度高、鲁棒性强且能抑制系统抖振的目的,本文设计了基于新型趋近律的反步滑模控制器.
2.1 引入滑模项设x1为小球在x轴方向的实时位置,xd为小球在x轴方向的期望轨迹位置,定义小球x轴位置跟踪误差为:
选取Lyapunov 函数为:
显然V1是连续正定函数.
对式(10)进行求导得:
为减小预定轨迹速度对系统影响,设计中间虚拟控制量为:
式中:c1>0.
将式(12)代入式(11)得:
为避免微分爆炸现象的发生,故引入动态滑模面S=0.设计切换函数为:
式中:k>0.
由于
故由式(14)与式(15)可得:
假设 1系统状态进入滑模面,即s=0时,由于k+c1>0,由 式(13)、(15)与(16)可 知,e1=0,e2=0,且1≤0,即保证了系统渐进稳定.为此需要进行下一步设计以保证系统能到达滑模面.
选取Lyapunov 函数为:
显然V2是连续正定函数.
对式(17)求导得:
将式(8)代入式(18)得:
2.2 新型趋近律与控制器设计引入滑动模态,可以使系统对系统部分结构不确定性、参数变化以及外界干扰等因素具有不敏感性和鲁棒性,而且还可获得良好的动态性能[20],但由于其自身存在不连续开关的特性,使得滑模变结构控制的抖振不能完全被消除.如若抖振问题不能很好地解决,可能会激发起系统的未建模高频特性,引起系统性能变差,严重影响控制器的性能.
为解决抖振问题,国内外学者设计了很多趋近律方法,但由于滑模控制的抗扰动与抗摄动机理,抖振是不可能完全被消除,只能根据需求削弱它.常用的传统趋近律有等速趋近律、指数趋近律与幂次趋近律.基于等速趋近律的控制策略很难达到收敛速度与消除抖振最佳状态,收敛速度较快,会在切换面附近引起较大抖振,为抑制抖振,必须以牺牲响应速度为代价;基于指数趋近律的控制策略虽然能在提高系统响应速度的同时抑制系统抖振,但是其抖振抑制能力有限;基于幂次趋近律的控制策略有较好的抖振抑制效果,能实现平滑进入滑模面,但是收敛速度有所欠缺.这几种趋近律均不能实现保证趋近速度的同时很好地抑制抖振的目的,为此,本文设计了一个分段变速趋近律.
设计趋近律为:
式中:k1>0,1 >α >0,1 >β >0,k为滑模面系数,f(x)为分段函数:
式中:Δ为滑模面边层厚度.
由式(20)和式(21)可知,本文设计的趋近律可保证系统状态在远离滑模面边层带时,可以迅速趋近,且趋近速度随着远离滑模面边层带的程度而呈现正相关.当系统状态进入边层带,即|s|<Δ时,由f(x)与 -k1|s|αsgn(s)可保证 系统能平滑且快 速地趋近滑模面.为增强所设计趋近律的通用性,在趋近律中增设1 /2k稳定项,以适用不同滑模面的设计.指数趋近律、幂次趋近律与本文设计新型趋近律的相轨迹如图4~6 所示.由图4~6 可知,相较于指数趋近律与幂次趋近律,本文所设计新型趋近律能使系统快速进入所设滑模面边层内,使其收敛速度加快,且系统进入边层与切换面交点后,系统抖振明显减弱,最终能平滑进入滑模面.故本文所设计趋近律不仅能提高趋近速度,还能有效抑制系统抖振,且通用性较强.

图4 指数趋近律相轨迹Fig.4 Phase trajectory of exponential reaching law

图5 幂次趋近律相轨迹Fig.5 Phase trajectory of power reaching law
由式(19)与式(20)可知,系统控制器为:
2.3 稳定性分析将式(20)代入式(19)得:
3 PSO 参数寻优
粒子群算法(Particle Swarm Optimization,PSO)是James Kennedy 等于1995 年提出的一种基于智能的优化算法[21].因其原理简单、易编码实现,其提出后便广泛应用于各领域.但PSO 算法同许多智能优化算法一样,存在容易陷入局部最优解的情况,为改善这一问题,本文对粒子群算法进行改进,提出了分段式寻优的PSO 策略.
3.1 优化目标为使系统能耗低和跟踪精度高,本文以上述系统为对象,为新型趋近律寻找一组最优参数以轨迹跟踪误差e1与系统控制器输出ux作为指标,建立目标函数如下:
3.2 PSO 算法改进由于PSO 算法与许多智能优化算法一样,存在容易陷入局部最优的缺陷,故本文提出了分段式权重分配方案.为增强本方案的通用性以及提高优化速度的同时规避陷入局部最优解,将粒子群全程迭代次数N分为3 个阶段.每个阶段赋予不同的权重,使其各个阶段达到相应目的,以保证最快搜寻速度找出全局最优解.
在前N/3次迭代内,赋予较大速度惯性权重与自我学习能力,降低群体学习能力,以达到较快速度搜寻出个体粒子的最佳位置的目的.权重赋值如下所示:
式中:w是速度惯性权重,c1是自我学习因子,c2是群体学习因子,wmax是所设置最大速度惯性权重,c1max是所设置最大自我学习因子,c2min是所设置最小群体学习因子.
为充分进行全局搜索,在中间N/3次迭代内,加入随机策略,对速度惯性权重、自我学习因子和群体学习因子进行随机取值,使得粒子历史速度对当前粒子速度无影响,且能保证尽可能地进行全局搜索,很好地规避陷入局部最优解.并且由于随机策略的引入,使得N的选择更为灵活,增强了算法的容错率.随机取值如下所示:
式(28)~(30)中,N(0,1)为标准正态分布,rand(0,1)为0 到1 之间的随机数,w是速度惯性权重,c1是自我学习因子,c2是群体学习因子.
本文在后N/3次迭代内,增大群体学习因子,降低速度惯性权重与自我学习因子,以实现粒子群体最终能快速收敛于群体最佳位置的目的,快速地求解出最优解.权重赋值如下所示:
式中:w是速度惯性权重,c1是自我学习因子,c2是群体学习因子,wmin是所设置最小速度惯性权重,c1min是所设置最小自我学习因子,c2max是所设置最大群体学习因子.
4 仿真实验
本文在Matlab 2018b 中进行仿真实验.设定板球系统预定轨迹为:
设定小球初始位置为(2,-1).防止中间虚拟控制量过大且要达到减小预定轨迹速度对系统影响的目的,因此本文选取c1=0.5. 由图6 可知,Δ过大会减弱系统前期收敛速度,由式(21)知 Δ <1会影响进入边层与切换面交点后对系统抖振抑制的效果,故选取 Δ=1.考虑到粒子种群数目越多越易发现全局最优解,但搜寻时间也会随之变长,故综合考虑选择粒子群初始种群为100.根据实验统计,当迭代次数选取为250 次及以下时,所得解不稳定,为求解稳定以及减少求解时间,因此在此基础之上加20 次迭代余量,故选取迭代次数为270 次.经过改进PSO 算法对新型趋近律参数寻优后选取k=1,k1=1.506 2,α=0.022 6,β=0.860 5,PSO 迭代曲线图如图7 所示,系统运行时间为4 s.本文进行了与Backstepping 控制策略和基于幂次趋近律的滑模控制方案的对比仿真实验.仿真结果如图8~12 所示.

图6 本文设计趋近律相轨迹Fig.6 Phase trajectory of reaching law designed by this paper

图7 PSO 迭代曲线Fig.7 PSO iteration curve

图8 轨迹跟踪对比Fig.8 Comparison of trajectory tracking
由图8~10 可知,本文提出控制策略的响应速度与控制精度均优于Backstepping 控制方法和幂次趋近律滑模控制方案.Backstepping 控制方法虽然响应速度比幂次趋近律滑模控制方案快,但由图8知,Backstepping 控制方法在抗扰动方面能力较弱,鲁棒性较差.而本文提出控制策略与幂次趋近律滑模控制方案均有很好的鲁棒性,且由图9 可知,本文提出控制策略在x方向上第一次进入并保持在稳态值5%内的调节时间为0.2 s,由于x轴和y轴是对称的,故系统调节时间为0.2 s,系统响应速度得到了很好地提高.由图11~12 可知,本文提出控制策略能较好地抑制系统抖振.

图9 x 轴轨迹跟踪对比Fig.9 Comparison of x-axis trajectory tracking

图10 y 轴轨迹跟踪对比Fig.10 Comparison of y-axis trajectory tracking

图11 x 轴幂次趋近律控制器输出Fig.11 The output of the power reaching law controller in the x-axis direction
通过3 种控制策略的仿真实验对比,可以看出本文提出控制策略无论是动态性能还是稳态性能均较优于其它两者,且能较好地抑制系统高频抖振,验证了所提控制方案的有效性.
5 结论
为了改善板球系统控制精度低、鲁棒性差以及响应慢等问题,本文提出了一种基于新型趋近律的反步滑模最优控制方案.将反步法与滑模控制相结合进行了分析,本文设计切换函数与新型趋近律并进行稳定性证明,最后引入PSO 算法,并改进PSO 算法进行参数寻优.仿真实验结果表明,提出的控制策略不仅改善了系统控制精度、鲁棒性与响应速度,而且控制器抖振问题得到了明显改善,具有良好的动态性能与稳态精度.下一步可以针对小球脱离板面的突变问题展开研究.

