基于指数目标函数优化的变压器局部放电故障最佳定位点估计方法

方子豪，陈潇一，孙佳伦

（1.湖北工业大学电气与电子工程学院，湖北武汉 430068；2.国网陕西省电力公司，陕西西安 710048；3.三峡大学电气与新能源学院，湖北宜昌 443000）

0 引言

由于变压器的绝缘破坏引起的局部放电（Partial Discharge，PD）故障，对于输配电网络的安全稳定运行具有重要的影响，因此针对变压器的PD故障定位点进行精确诊断是当前的一项重要的研究课题[1-5]。

在当前比较流行的定位点诊断方法中，主要是声发射传感器（Acoustic Emission Sensors，AES）法[1-2]与超高频法[3-4]（Ultra-High-Frequency，UHF）2 种方法。UHF 的优点是灵敏性能好，且具有很好的抗干扰性能，但是该方法要求提前将传感器布置在变压器内部，以避免外壳的电磁屏蔽，因此给该方法的广泛使用带来了较大的局限性。AES 法则不同，传感器可布置在变压器外壳上，因此受到了广泛的欢迎[6-8]。

AES 法的主要原理是利用声波到达不同的传感器的时间不同，根据不同的传感器建立不同的定位方程，然后联立方程进行求解，以得到PD 故障定位点的坐标[9-11]。然而，由于传感器在使用过程中不可避免的带有测量误差以及系统中不可避免的系统噪声干扰，因此采用AES 法得到的数据严格来讲不可能都是精确无误的，同时在实际使用的时候，为了防止个别传感器的失效，传感器的布置总是会多于实际需要的个数，以满足冗余的要求[9-11]。由于精确无误的值在实际中是不可能得到的，为此采用AES 法进行PD 故障定位点的诊断过程，实际上是一个属于PD 故障定位点最佳估计的问题，该问题在本质上与在电力系统状态估计（State Estimation，SE）中，通过利用数据采集与监视控制（Supervisory Control and Data Acquisition，SCADA）系统、高级量测体系（Advanced Metering Infrastructure，AMI）等量测系统，采集量测数据以获取系统最真实的SE 结果是相同的[12-16]。

为此，本文针对采用AES 法测量PD 故障定位点，同时考虑多个冗余AES 及其测量误差，提出了基于指数目标函数优化的变压器局部放电故障定位点最佳估计方法。首先，该方法借鉴状态估计中的量测方程概念，构造PD 故障定位点量测方程；然后，针对多个冗余AES 定位点量测方程，以指数型误差最小构造目标函数，并采用牛顿法迭代求解，得到变压器PD 故障定位点的最佳估计值；最后，基于仿真实验对本文所提方法的有效性进行验证。

1 变压器PD故障定位理论

1.1 AES法定位原理

根据声波到达不同传感器的时间，建立不同的传感器定位方程，在三维坐标系中，以声波到达参考传感器（1 号传感器）的时间作为参考基准，声波达到第i（i＝2，3，…，m）个传感器与参考传感器的时间之差为τi1，则为定位PD 故障点，状态变量共4个，分别为PD 故障定位的(x,y,z)坐标值以及PD 故障源声信号至参考传感器所用的时间t。为了方程可解，PD 故障源声信号至参考至少需采用4 个AES 传感器，才可建立方程进行求解。假设变压器PD 源的坐标为P(x,y,z)，AES 传感器的个数为m个（m>4），其坐标为Si(xi,yi,zi)，由此可建立AES 法的定位方程如下[10-13]：

式中：t为PD 故障源声信号至参考传感器所用的时间；v为声波速度。

1.2 定位量测方程

由于传感器在使用过程中不可避免地带有测量误差以及系统中不可避免的系统噪声干扰，为此本文定义以下定位量测方程[14-15]：

式中：Z为量测量；h(X)为量测方程；X为状态量，X=[x,y,z,t] ；ε为假设服从Gauss 分布的量测误差。

Z可通过构造以作为伪量测，具体表达式为：

式中：Zi为第i（i＝2，3，…，m）个伪量测；

h(X)具体表达式为：

通过定义和构造，本文创造性地将高电压与绝缘领域的AES 法进行PD 故障定位点的诊断问题研究，转换为根据已知伪量测和量测方程，利用系统的冗余传感器数据，考虑测量时间误差，求解系统最佳定位点状态量的估计结果问题。

2 PD 最佳定位点指数目标优化估计模型

在考虑多个冗余AES 及其测量误差基础上，本文借鉴SE 领域的量测和量测方程概念，构造了伪量测Z和量测方程h(X)。在SE 领域，为处理多个冗余量测、量测误差以及可能的坏数据，建立优化模型并求解，以得到最接近真值的估计值。由于在实际中，毫无误差的精确真值是不可能获得的，因此估计并不意味着不精确，恰恰是在优化模型下寻找到的最接近真值的值。

为此，本文在将高电压与绝缘领域的AES 法进行PD 故障定位点的诊断问题转化为SE 问题后，建立PD 故障定位指数目标优化模型，首先将量测残差指数化，以残差的指数形式之和J为优化目标，所建模型为：

式中：下标i表示第i个量测；wi为权重，AES 测量精度越高，权重越大，对估计结果的贡献越大；ri为示残差；σ为量测标准差；j为AES 重复测量个数。

为了增大量测冗余度，每个AES 可测量多次，得到多个量测值。

本文建立的指数目标优化估计模型的优点在于目标函数连续可微，利于求解，且残差指数化后，对于量测误差大甚至可能的坏数据，其在模型中对最终估计结果的影响更小，抑制了大误差和坏数据的干扰。

令：

式中：rwi为正则化残差，其作用在于可将不同类型的物理量归一到同一个尺度上，以便于比较；fi(X)为残差的指数形式。

则指数目标优化模型可转化为：

为说明误差大的量测及坏数据对权重的影响，绘制fi(rwi)与rwi关系如图1 所示。

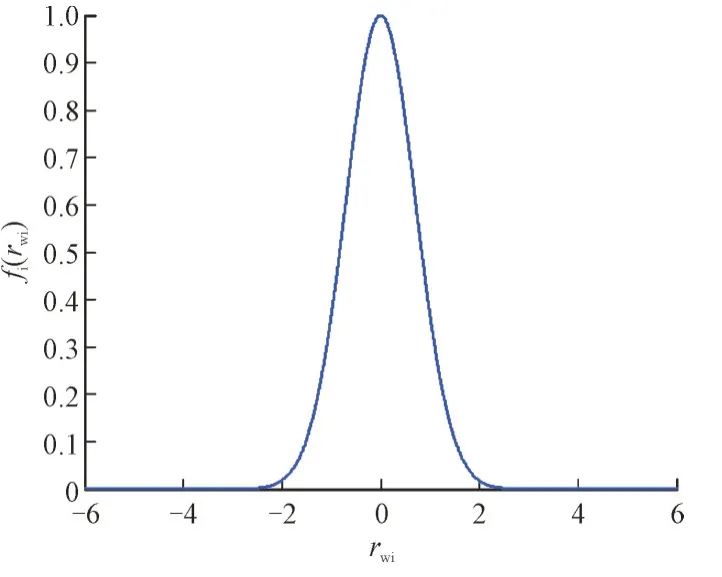
图1 fi(rwi)与rwi 关系曲线Fig.1 Relation curve Between fi(rwi) and rwi

由图1 可知，rwi的绝对值越大，说明其误差越大甚至可能是坏数据，fi(rwi)就越小，对优化目标的贡献就越小，对估计结果的影响也就越小；反之，rwi的绝对值越小，说明该量测的精度就越高，fi(rwi)就越大，对优化目标的贡献就越大，对估计结果的影响也就越大，越有利于得到更精确的估计结果。故而本文模型可以削弱和抑制AES 量测误差甚至是坏数据的影响，得到最佳的PD 故障定位点估计结果。

3 PD 最佳定位点指数目标优化估计算法

为求解PD 最佳定位点指数目标优化模型，采用Newton 法迭代进行求解，先求目标函数的1 阶偏导数为：

式中：H为量测方程h(X)对状态量X的（k×m）×n维的Jacobian 矩阵；F(X)为对角阵；Fii(X)为F(X)第i个对角元。

对式（10）一阶偏导∂J/∂X再求一次偏导，可得目标函数二阶偏导式为：

式中：I为单位阵；Q为目标函数2 阶偏导阵。

Newton 法迭代PD 最佳定位点状态量的修正量计算式为：

式中：k为迭代次数。

状态量修正表达式为：

收敛条件设为：

式中：γ为收敛阈值。

通过指数目标优化估计算法，对PD 最佳定位点指数目标优化模型进行计算，收敛后即可获取PD 故障最佳定位点的估计值，其详细计算步骤如下：

1）先用高斯赛德尔法迭代2 次，获取指数目标优化估计的Newton 法状态量初值X(k)，设置最大迭代次数kmax、收敛精度γ和量测固定权重wi，设置迭代次数k=0。

2）根据X(k)，基于计算式（10）与式（11）中PD最佳定位点指数目标优化模型的1 阶、2 阶偏导阵。

3）基于计算式（12），计算修正量ΔX(k)。

4）若max(|ΔX(k+1)|)<γ，则算法收敛转步骤6）。否则，更新状态量：X(k+1)=X(k)+ΔX(k)，转步骤5）。

5）令k=k+1，转步骤（2）。

6）输出计算结果。

PD 最佳定位点指数目标优化算法如图2 所示。

图2 PD最佳定位点指数目标优化算法Fig.2 Exponential target optimization algorithm of PD optimal locating point

4 算例仿真与分析

4.1 基础数据与仿真条件

为对本文所提基于指数目标函数优化的变压器局部放电故障定位点最佳估计方法的有效性进行验证，在150 cm×100 cm×120 cm 大小的变压器内设置PD 故障点，其真实坐标为P（80，55，60）cm。本文采用的AES 设备数为10 个，具体坐标为S1（15，0，15）cm，S2（10，80，20）cm，S3（120，80，10）cm，S4（130，10，15）cm，S5（25，20，110）cm，S6（15，110，110）cm，S7（120，80，110）cm，S8（130，20，110）cm，S9（90，30，100）cm，S10（110，40，80）cm，每个AES重复测量3 次，在变压器油中声波速度大小为1 500 m/s。

以S1（15，0，15）cm 位置的AES 作为参考传感器，为模拟产生AES 的量测数据，在声波到达第i个传感器与参考传感器的时间之差τi1真值基础上，叠加均值为0、标准差为0.2%的高斯噪声，以作为AES 的随机量测数据。

为验证本文所提方法可有效抵御量测误差以及可能的坏数据的对估计结果的影响，获取最接近真实PD 故障的最佳定位点，在量测为真值、考虑量测误差但无坏数据和考虑量测误差且有坏数据3种情况下，分别采用以下3 种方法分别进行仿真分析：（1）普通AES 定位法；（2）基于K-means 聚类的AES 法；（3）本文所提方法。坏数据的设置为假设8号S8（130，20，110）cm 位置的AES 损坏，测量数据严重失真，误差为50%。

利用下列指标对各种方法所得结果进行评价，如式（15）—式（19）所示：

式中：ΔR为PD 故障定位点估计误差；xact,yact,zact为PD 故障定位点真值；xe,ye,ze为PD 故障定位点估计值；Δx为PD 故障定位点x轴估计误差；Δy为PD 故障定位点y轴估计误差；Δz为PD 故障定位点z轴估计误差；Dmax为PD 故障定位点x，y，z轴最大估计误差。

4.2 仿真结果与分析

在量测为真值、考虑量测误差但无坏数据和考虑量测误差且有坏数据3 种情况下，普通AES 定位法、基于K-means 聚类的AES 法和本文所提方法的仿真结果如表1—表3 所示。

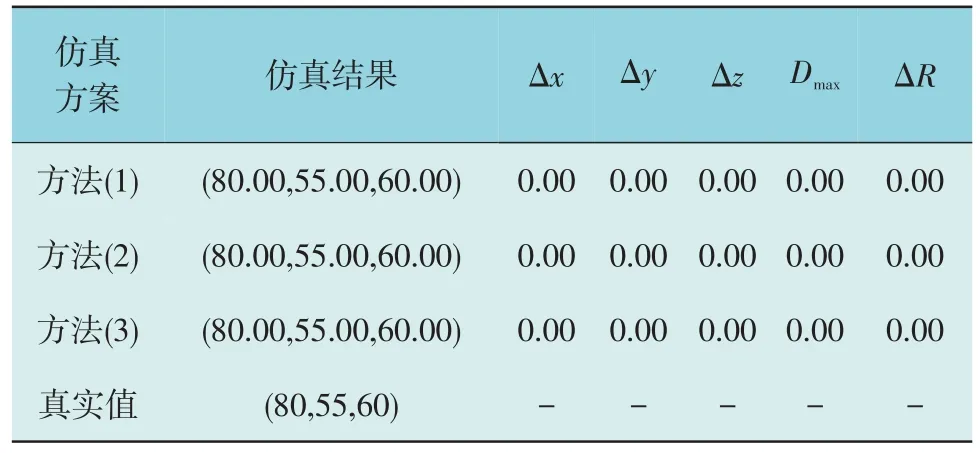
表1 真值量测下PD故障定位点计算结果Table 1 Calculation results of PD fault location under true value measurement cm

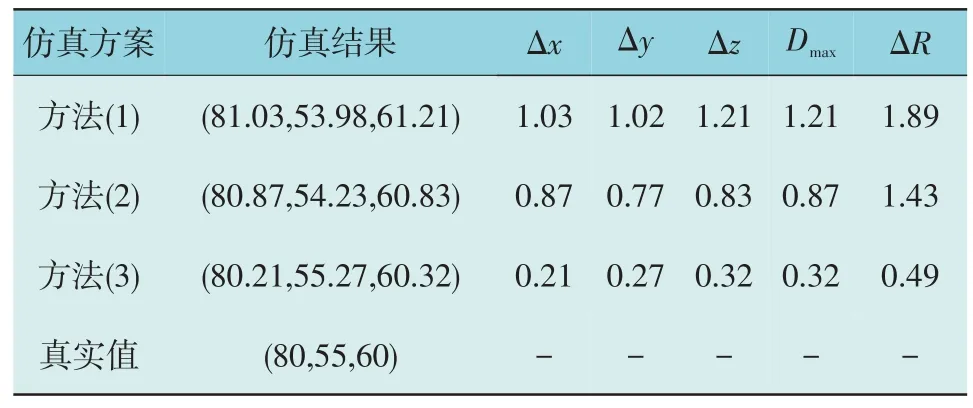
表2 考虑量测误差但无坏数据下PD故障定位点计算结果Table 2 Calculation results of PD fault location considering measurement error but no bad data cm

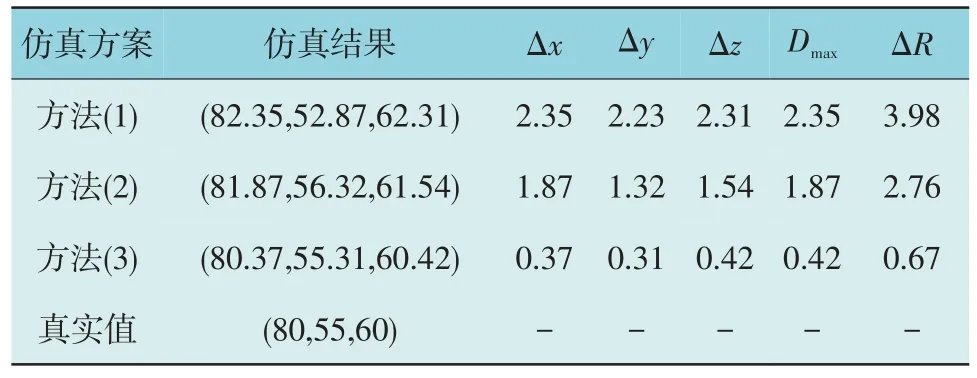
表3 考虑量测误差且有坏数据下PD故障定位点计算结果Table 3 PD fault location calculation results considering measurement error and bad data cm

由表1 可知，在量测为真值的情况下，PD 故障点真值坐标为（80，55，60）cm，3 种方法的PD 故障定位点结果均为（80.00，55.00，60.00）cm，Δx，Δy，Δz，Dmax和ΔR指标均为0.00 cm，说明3 种方法在真值量测下均可获得精确的PD 故障定位点结果。然而，在实际中真值量测无法真实获取，由于不可避免的噪声干扰在一定程度上都带有误差甚至是坏数据，因此真值量测是一种理想情况，在实际中并不存在。

由表2 可知，在考虑量测误差但无坏数据的情况下，3 种方法的PD 故障定位点结果分别为（81.03，53.98，61.21）cm，（80.87，54.23，60.83）cm 和（80.21，55.27，60.32）cm。方法（1）普通AES 定位法的Δx，Δy，Δz，Dmax和ΔR指标分别为1.03 cm，1.02 cm，1.21 cm，1.21 cm 和1.89 cm；方法（2）基于K-means 聚类的AES 法的Δx，Δy，Δz，Dmax和ΔR指标分别为0.87 cm，0.77 cm，0.83 cm，0.87 cm 和1.43 cm；方法（3）本文所提方法的Δx，Δy，Δz，Dmax和ΔR指标分别为0.21 cm，0.27 cm，0.32 cm，0.32 cm 和0.49 cm。由此可知，在有量测误差时，3种方法的PD 故障定位点结果与真实值PD 点均有所误差，但本文由于将该定位点计算问题转化为定位点SE 问题，有效的滤除了量测误差的影响，估计指标最好，估计结果最精确。

由表3 可知，在考虑量测误差且有坏数据的情况下，3 种方法的PD 故障定位点结果分别为（82.35，52.87，62.31）cm，（81.87，56.32，61.54）cm 和（80.37，55.31，60.42）cm。方法（1）普通AES 定位法的Δx，Δy，Δz，Dmax和ΔR指标分别为2.35 cm、2.23 cm、2.31 cm、2.35 cm 和3.98 cm；方法（2）基于K-means 聚类的AES 法的Δx，Δy，Δz，Dmax和ΔR指标分别为1.87 cm、1.32 cm、1.54 cm、1.87 cm 和2.76 cm；方法（3）本文所提方法的Δx，Δy，Δz，Dmax和ΔR指标分别为0.37 cm、0.31 cm、0.42 cm、0.42 cm 和0.69 cm。与表2 相比，在有量测误差且有坏数据时，方法（1）的PD 故障定位点结果与真实值PD 点的误差将显著增大，主要原因在于普通AES 法不具有抵御坏数据的能力。方法（2）的PD故障定位点结果与真实值PD 点的误差增大较多，主要原因在于相比普通AES 法基于K-means 聚类能在一定程度上稀释坏数据的影响，但无法完全避免。方法（3）的PD 故障定位点结果与真实值PD 点的误差基本不变，主要原因在于本文将PD 故障定位点计算问题转化为SE 问题后，建立指数目标最优模型并进行求解，不但能够有效滤除量测误差，且对坏数据有良好的抵御能力，坏数据对优化模型的贡献度非常低，对估计结果影响非常小，从而有效的保证了估计结果的精度不受影响。

5 结论

本文针对采用AES 法测量PD 故障定位点，同时考虑多个冗余AES 及其测量误差，提出了基于指数目标函数优化的变压器局部放电故障定位点最佳估计方法。该方法具有以下特点：

1）借鉴SE 理论，定义了伪量测和构造了PD 故障定位点量测方程，创造性地将高电压与绝缘领域的AES 法进行PD 故障定位点的诊断问题，转换为根据已知伪量测和量测方程求解PD 最佳定位点的SE 优化问题。

2）针对多个冗余AES 定位点量测方程，以残差指数形式构造指数目标函数优化模型，并采用牛顿法迭代求解，该方法能够有效的滤除量测误差和抵御坏数据的影响。

通过仿真实验对本文所提方基于指数目标函数优化的变压器局部放电故障定位点最佳估计方法进行验证，结果表明本文所提方法可以高精度的定位变压器PD 故障点，有效的进行变压器PD 故障定位点的诊断。