高速公路隧道环境驾驶人视觉注视转移特性研究

张广乐、贾磊

（1.中铁上海工程局集团第四工程有限公司，上海 201906；2.交通运输部公路科学研究院，北京 100088）

1 试验设计

1.1 试验隧道路段

此次研究选择国道109 高速公路二工区作为试验隧道路段（西六环—市界段），隧道采用左、右分离的独立双洞的平面布设形式，左线长为3401m，右线长为3479m，全长为6880m。

1.2 试验时间、天气以及隧道路段

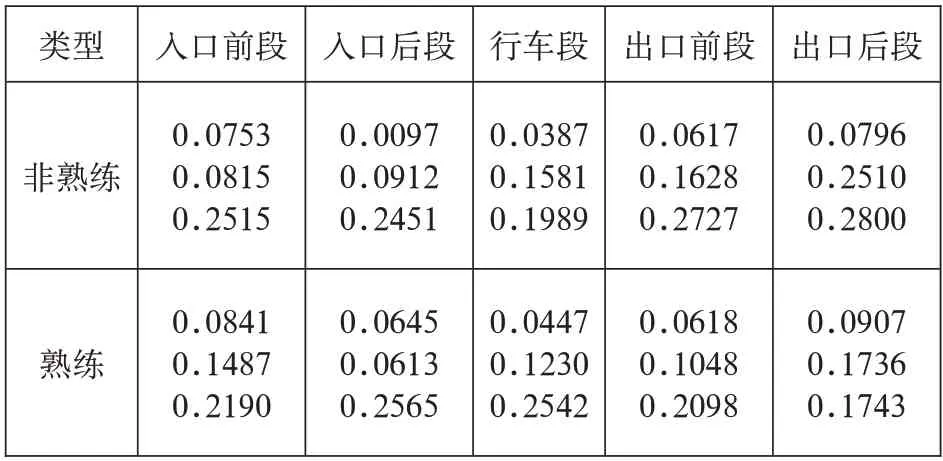
基于早晚高峰的考虑，此次试验选择了在天气晴朗的工作日展开，时间为9:30—16:30，平均光照强度为33000Lx。隧道划分为入口段、行车段以及出口段，入口段600m 分别由入口前段300m 与入口后段300m组成，出口段亦如此，剩下中间路段为隧道行车段。试验隧道路段光照强度由车载照度仪完成采集[1]。

1.3 被试人及仪器设备

试验所选择的人员由5 名娴熟驾驶人和5 名非娴熟驾驶人构成，被试人全身功能正常且矫正视力都在5.0 以上。试验车辆为轿车，仪器装置中使用了采样频率为60Hz 的头戴式Dikablis 眼动仪，部分试验数据由配置的D-Lab 驾驶行为分析系统获取。

1.4 试验过程

试验中需携带眼动仪，由试验起始点行驶至结束点。为了确保数据的准确性，每名测试对象均进行了3 次试验，取均值作为试验数据展开分析。

2 高速公路隧道环境驾驶人视觉注视转移特性研究

2.1 隧道环境下驾驶人注视点分布特性

以5 名视力差异较大的测试对象作为兴趣区域划分的研究对象，即对每位驾驶人行驶时的12000±10%个注视点坐标进行提取，并使用K 均值聚类算法完成对注视点坐标进行聚类[2]。聚类结果如图1 所示。

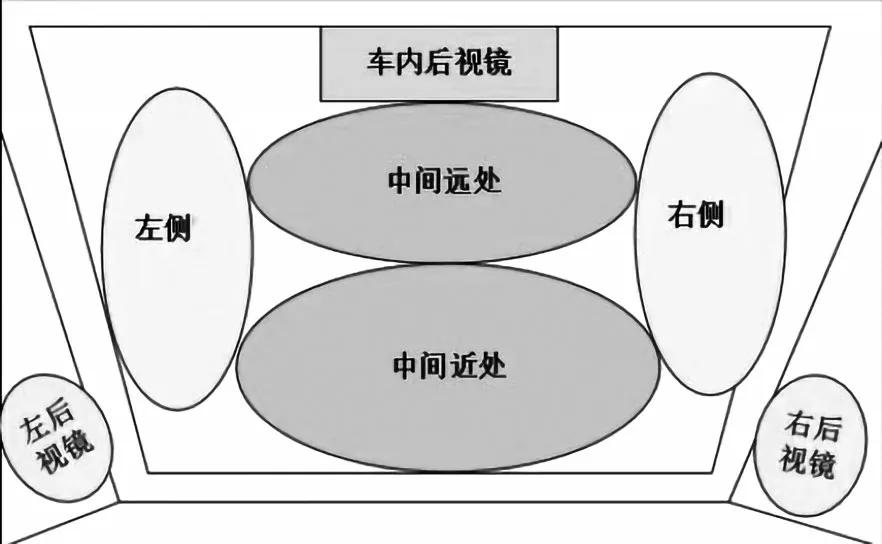
图1 注视区域聚类结果

深入研究入口段、行车段与出口段驾驶人在注视点分布上的差异与比例，所得数据如图2 所示。

图2 隧道不同路段注视点分布比例

2.2 隧道环境下驾驶人注视点转移特性

2.2.1 马尔可夫链

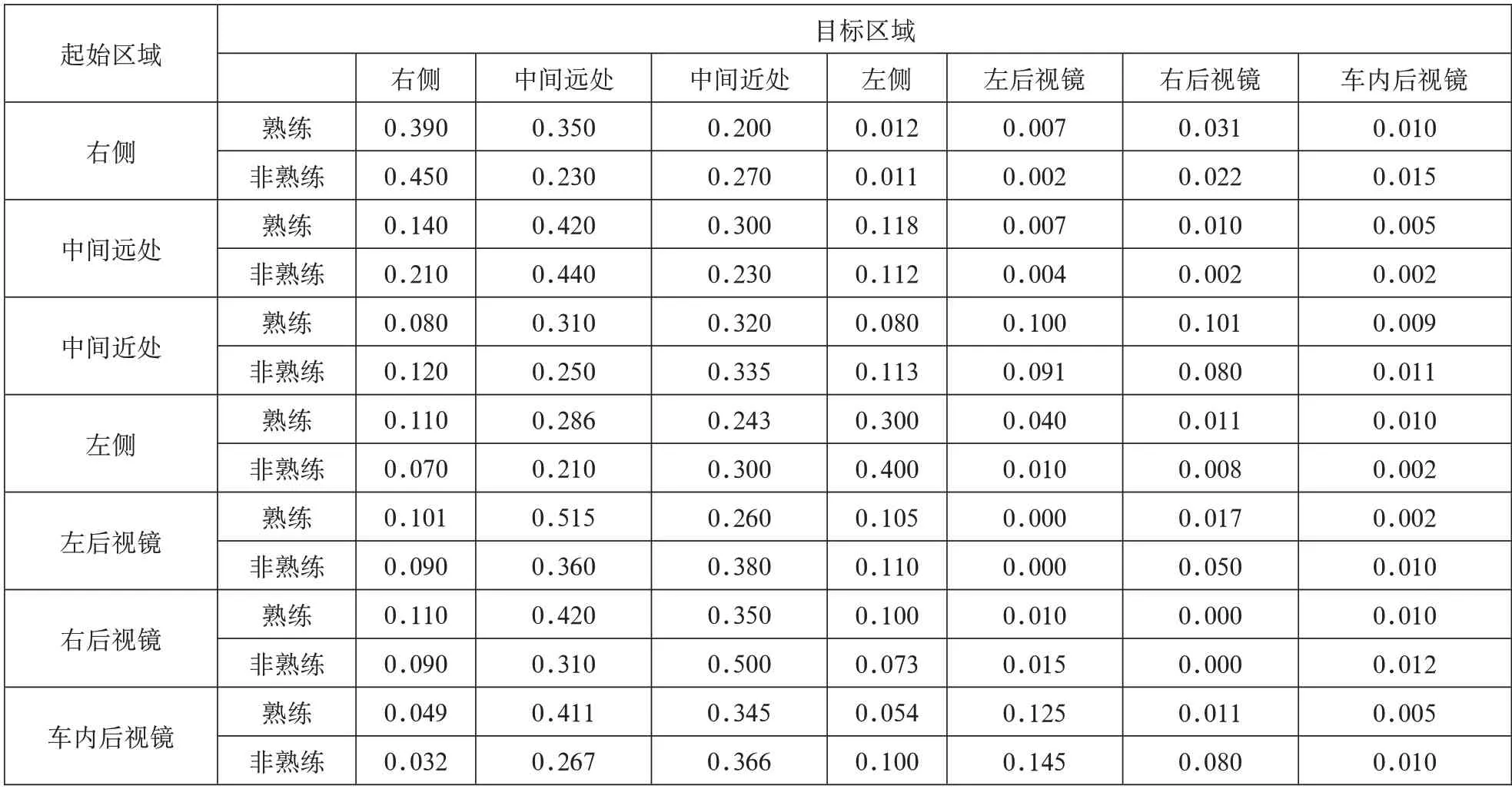
设随机序列{X(n),n=0,1,2,…} 的离散状态空间E为 {1,2,…}，若对于任意m个非负整数n1,n2,…,nm( 0 ≤n1

则称{X(n),n=0,1,2,…} 为马尔可夫链。在这一模型下，时刻t的状态仅与前一个时刻t−1 的状态相关，与其他时刻所处的状态无关，表现出十分显著的无后效性随机过程。

2.2.2 注视一步转移概率矩阵计算

条件概率形式如式（2）所示：

即马尔可夫链在时刻的步转移概率。在知道时刻处于状态i的情况下，经过k个步骤后系统处于状态j的概率称为转移概率。如果转移概率不依赖于时刻，那么便与起点无关，则称为齐次马尔可夫链。

上述转移概率可表示为Pij(n,n+k)，记为Pij(k)，当k=1 时，Pij(1)称为一步转移概率。

设P为一步转移概率Pij(1)所组成的矩阵，则有式（3）：

为系统状态的一步转移概率矩阵。

在此次研究中，借助马尔可夫链理论，并应用统计估算的方法对驾驶人在各视觉兴趣区域间的一步转移概率进行求解。

2.2.3 基于马尔可夫链的注视转移概率分析

基于不同的注视兴趣区域，分别对试验中5 名熟练驾驶人与5 名非熟练驾驶人的注视数据进行统计分析，取其均值。然后应用统计估算的方法对驾驶人在隧道5 个不同区段的注视一步转移概率矩阵进行求解，具体结果如表1、表2、表3 所示。

表1 高速公路隧道入口段的注视一步转移概率分布

表2 高速公路隧道行车段的注视一步转移概率分布

表3 高速公路隧道出口段的注视一步转移概率分布

2.2.4 基于马尔可夫链的注视行为平稳分布分析

设{Xn},n=0,1,…,n是齐次马尔可夫链，状态空间为I,转移概率为Pij,存在概率分布{πi,j∈I},若有式（4）：

则称{πi,j∈I} 为马尔可夫链的平稳分布。基于马尔可夫链平稳分布这一特性，当驾驶人行进时间较长后，其注视点分布的概率会逐渐稳定。

为此，可以借助不同经验驾驶人在隧道5 个不同区段的注视一步转移概率建立七元一次方程组，如式（5）所示：

详解如表4 所示，其中每列矩阵中的数值从上至下依次为1—7 区域的注视平稳分布概率。

表4 隧道5 个不同区段的注视平稳分布

3 结论

第一，在隧道路段，驾驶人很少将视线转移到左后视镜区域、右后视镜区域以及车内后视镜区域，并且重复观察的概率相当小，主要的注意力放在了中间区域，即更强调前方道路状况。

第二，通常情况下，驾驶人视觉转移往往集中在左、右侧区域及中间区域，在进入特殊路段时，驾驶人重复上述区域注视转移的概率会大大增加。

第三，当驶至隧道入口段时，驾驶人会将视线重复转移至右侧区域与中间近处区域，这与入口段车流密度较大有关。

综上所述，此次研究取得了一定的成果，但仍有待进一步深入，以期为保障高速公路隧道行车安全做出更多贡献。