井下水仓正铲清挖机构运动学及动力学分析

毛 君，李 博，谢 苗，刘治翔，李玉岐，王 帅，董钰峰，侯文博，田 博

（辽宁工程技术大学 机械工程学院，辽宁 阜新 123000）

0 引言

随着矿山机械化程度的不断提高，机械化清仓逐渐成为主流。目前国内煤矿主要采用清仓机和装载机清理水仓煤泥，现有井下水仓清挖机构多为螺旋机构，当煤泥含水量过高或过低时清挖效率会大幅降低。少数煤矿采用装载机进行清仓，当清理含水率较高的煤泥时，矿车运输途中容易洒漏。

国内外学者对井下水仓清挖机构和挖掘机构进行了大量研究。GAO等[1]建立了螺旋集料装置工作过程的离散数值模型，得出了螺旋轴转速、进料口顶部倾角和抛板数量三个关键参数对物料运输效率的影响。郭培红等[2]对防黏料无轴螺旋技术、防泄漏双螺旋上料技术、蛙形自行走技术、逻辑型全液压控制技术等进行了研究，提出了一种煤泥清挖泵送一体机。张兰锁等[3]根据国内大部分水仓中煤泥性质提出了一种挖斗式清仓结构，填补了我国井下自行式铲斗清仓机的空白。LI等[4]提出了一种新型液压挖掘机铲挖机构，通过仿真证明了所提出的装置具有很好的性能。刘畅等[5]采用多体机械系统仿真软件对工作装置进行运动学和动力学仿真分析，得到各杆件之间铰接点的位移与速度曲线。刘晓亮[6]通过在虚拟样机模型中输入各个液压缸随时间变化的数据，提取出了各构件的角速度和角加速度随时间变化的数据。SALINIC等[7]以凯恩方程的形式给出了液压挖掘机的运动微分方程，并探究了挖掘、提升和卸载等过程对挖掘机的影响。SALIKHOV等[8]研究了单斗挖掘机作业时间对其作业性能影响，确定了土壤挖掘的最佳技术参数。以上对井下水仓清挖机构的研究主要是针对螺旋机构进行的，对挖掘机构的研究主要是对传统的铲挖及运动方式的研究，对大翻转角度自装载的铲挖机构及运动方式的研究较少。

本文以煤矿井下水仓清挖机构为背景，研究一种具有大翻转角度的井下水仓清挖机构，并进行相应的运动学和动力学分析，得出井下水仓清挖机构的运动学和动力学特性。

1 井下水仓清挖机构基本结构和工作原理

1.1 井下水仓清挖机构

定义顺时针为负方向，设计井下水仓清挖机构示意见图1，结构参数见表1。

表1 井下水仓清挖机构主要参数Tab.1 main parameters of clearing mechanism of well sump

图1 井下水仓清挖机构示意Fig.1 schematic of clearing mechanism of well sump

1.2 井下水仓清挖机构工作原理

如图2所示，井下水仓清挖机构工作过程主要分为三个步骤。

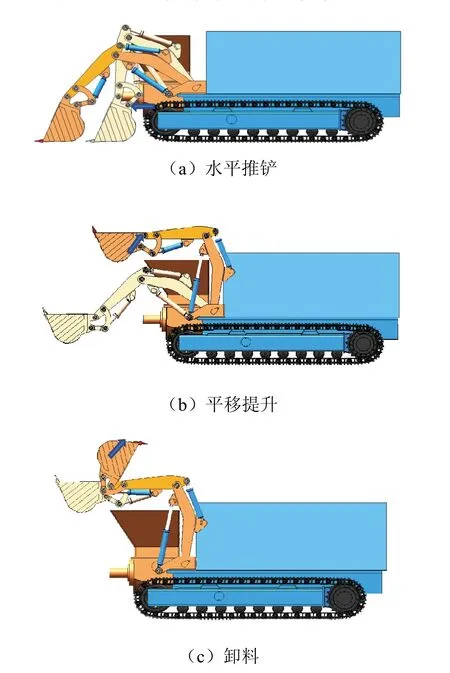
图2 井下水仓清挖机构工作过程Fig.2 the working process of the cleaning mechanism of well sump

（1）水平推铲：小臂液压缸、大臂液压缸和铲斗液压缸全部进行收缩，此时铲斗相对于地面的角度变化较小，铲斗向前推移，实现井下水仓清挖机构在水平面上推铲的动作。

（2）平移提升：铲斗液压缸收缩，大臂液压缸和小臂液压缸伸长实现井下水仓清挖机构的平移提升，此时铲斗相对于地面的角度变化较小，实现铲斗平移提升。

（3）卸料：大臂液压缸和小臂液压缸锁定，铲斗液压缸伸长，卸料至机身物料泵内，实现铲运一体。

2 运动学仿真分析

2.1 运动学正反解分析

根据多环路耦合机构的结构特点，将煤矿井下水仓清挖机构划分成4个基本运动链环路进行分析。利用大臂液压缸、小臂液压缸和铲斗液压缸的工作行程x1、x2和x3作为输入量，求解井下水仓清挖机构铲斗末端位置（LX，LY）和姿态转角φ，定义顺时针方向为负，环路图见图3。图3中，θ1为点A与点E连线与水平面之间的夹角，β2为点F与点J连线与水平面的夹角，θ2为点A与点E连线延长线与点E与点J连线的夹角，η为点E与点J与水平面的夹角，ζ为点A与点F连线与水平面之间的夹角，θ3为点E与点J连线延长线与点J与点L连线的夹角，以上夹角单位为°。

图3 井下水仓清挖机构环路Fig.3 loop of clearing mechanism of well sump

运动学正解参数方程如下。

在环路C1中，

在环路C2中，

在环路C3中，

在环路C4中，

式（1）～式（11）中：EX、EY分别为点E的横向坐标和纵向坐标；JX、JY分别为点J的横向坐标和纵向坐标；lAF为大臂-安装座铰点A与小臂-小臂液压缸铰点F距离；lJH为铲斗-小臂铰点J与连杆一-连杆二铰点H距离。

井下水仓清挖机构运动学反解是在获得井下水仓清挖机构铲斗末端位置（LX，LY）和姿态转角（φ）后，求出3组液压缸的输入长度，反求J、F、E点的位置坐标。

运动学反解参数方程为

在环路C1中，

在环路C2中，

在环路C3、C4中，

2.2 正反解验证

给定三组驱动液压缸工作形成变化见图4。

图4 液压缸输入Fig.4 hydraulic cylinder input

水平推铲阶段：在0～3 s内，大臂液压缸工作行程x1由784 mm缩短至694 mm，小臂液压缸工作行程x2由771 mm缩短至639 mm，铲斗液压缸工作行程x3由563 mm缩短至454 mm。

铲挖阶段：在3～8 s内，大臂液压缸工作行程x1和小臂液压缸工作行程x2无位移变化，铲斗液压缸工作行程x3由454 mm伸长到634 mm。

平移提升阶段：在8～13 s内，大臂液压缸工作行程x1由694 mm伸长到1063 mm，小臂液压缸工作行程x2由639 mm伸长至682 mm，铲斗液压缸工作行程x3由634 mm缩短至525 mm。

卸料阶段：在13～18 s内，大臂液压缸工作行程x1和小臂液压缸工作行程x2无位移变化，铲斗液压缸工作行程x3由525 mm伸长到728 mm。

由运动学正解求得齿尖位置（LX,LY），见图5（a）和图5（b），姿态角（φ）见图5（c）。由图5（c）可知，井下水仓清挖机构在8～13 s提升过程中保持姿态角不变，有效避免了煤泥洒漏。

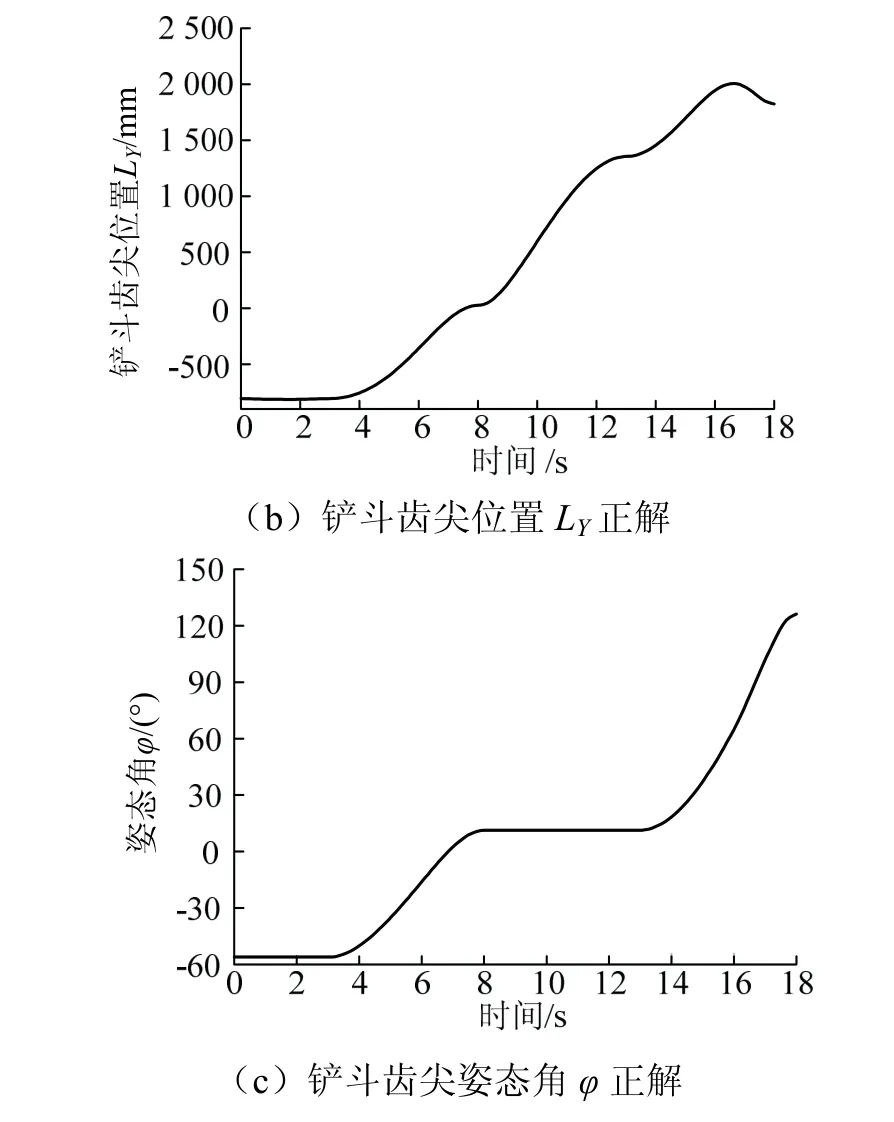
图5 运动学正解输出Fig.5 kinematics forward solution output

将求得的运动学正解设为反解求解的输入值，求解后得到该井下水仓清挖机构三组液压缸运动学反解输出值，见图6。绘制正反解误差曲线见图7。

图6 运动学反解输出Fig.6 kinematics forward solution output

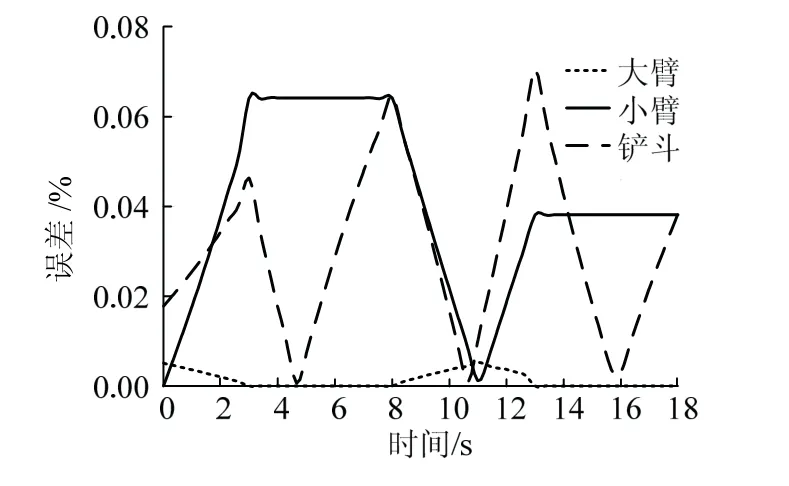
图7 误差曲线Fig.7 error curve

通过图7可知，正反解输出值之间存在微小的误差，这是由于小数取舍造成的，可以忽略不计，验证了该运动学正解与反解模型的正确性。

2.3 虚拟样机建立

将Solidworks三维模型导入到ADAMS中，并添加相关约束。设置液压缸驱动函数如下。

（1）大臂：

step(time,0,0,3,-90)+step(time,3,0,8,0)+step(time,8,0,13,369)+step(time,13,0,18,0)；

（2）小臂：

step(time,0,0,3,-132)+step(time,3,0,8,0)+step(time,8,0,13,43)+step(time,13,0,18,0)；

（3）铲斗：

step(time,0,0,3,-109)+step(time,3,0,8,180)+step(time,8,0,13,-109)+step(time,13,0,18,203)。

建立虚拟样机模型见图8。

图8 虚拟样机模型Fig.8 virtual prototype model

对模型约束进行检验，结果表明模型无冗余约束，验证了虚拟样机三维模型的正确性。

2.4 运动学仿真对比分析

在铲斗齿尖创建点MARKER_219，跟踪其运动轨迹，仿真结束后得到井下水仓清挖机构的清挖轨迹见图9。

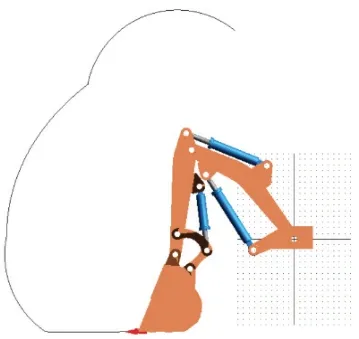
图9 清挖轨迹Fig.9 clearing track

将仿真结果和运动学正解理论计算值进行对比分析，见图10。

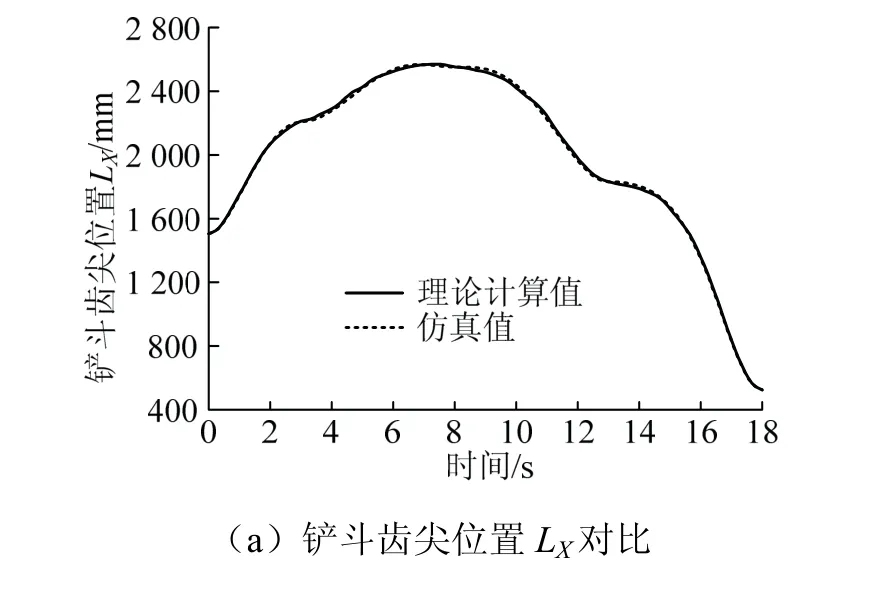
图10 仿真与理论计算结果对比Fig.10 comparison of kinematic parameters

由图10中可知，铲斗齿尖位置LX的理论计算值与仿真值均在500～2600mm内变化，铲斗齿尖位置LY的理论计算值与仿真值均在-800～2000 mm内变化，铲斗齿尖姿态角φ的理论计算值与仿真值均在-58°～130°内变化，且理论计算值与仿真值得到的曲线走势基本一致，仅存在微小的偏差，在可接受的范围内，证明了所建仿真模型的准确性。

2.5 井下水仓清挖机构各关节角及角速度仿真

为了证明井下水仓清挖机构的平稳性，通过ADAMS运动学仿真模型，测得井下水仓清挖机构各关节的角位移和角速度见图11和图12。

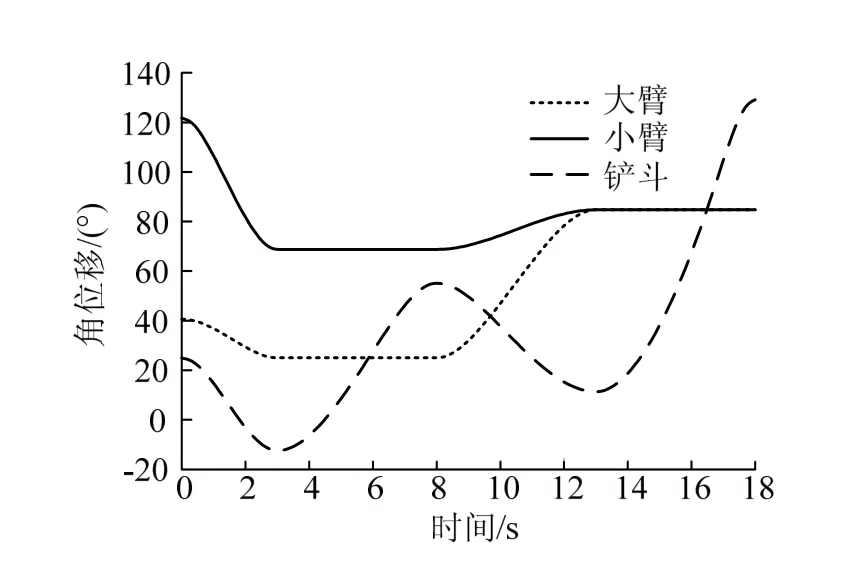
图11 各关节角位移Fig.11 joint angle motion

图12 关节角速度Fig.12 joint angular velocity

由井下水仓清挖机构运动学曲线分析可知井下水仓清挖机构在运动过程中，曲线变化较平稳连续，无突变，符合实际要求。

3 ADAMS动力学仿真分析

3.1 井下水仓清挖机构关节驱动力矩分析

将井下水仓清挖机构分为两部分：三连杆机构系统和液压缸-连杆系统，采用拉格朗日法建立系统的逆动力学理论模型[9]，受力分析见图13。

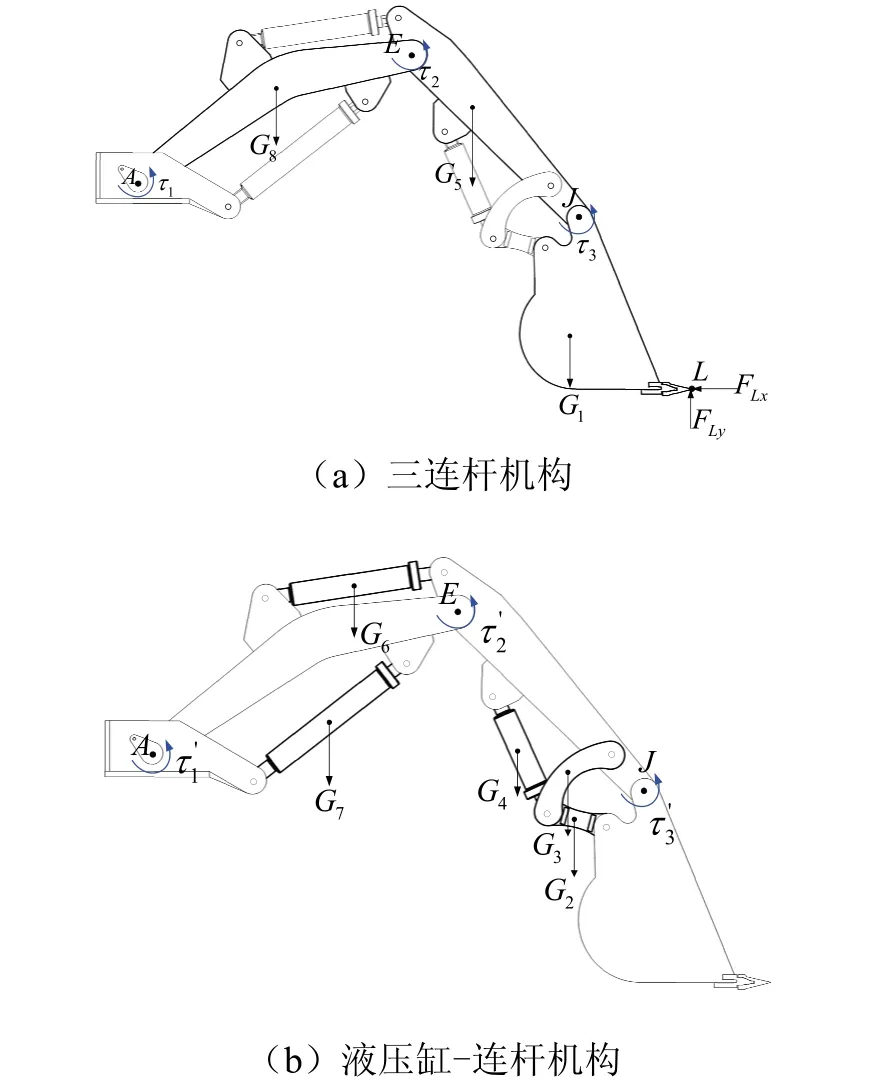
图13 井下水仓清挖机构受力分析Fig.13 driving torque of clearing mechanism of well sump

将点A所在的水平面设为基准面，势能、动能分别为

式中：Ti为构件i动能，J；Vi为构件i势能，J；Gi为构件i重力，N；mi为构件i的质量，kg；hi为构件i中心相对于基准点A的竖直距离，m；vi为构件i质心的运动速度，m/s；Ji为构件i的转动惯量，kg·m²；wi为构件i的旋转角速，rad/s；i为构件编号，i=1,…,8。

（1）三连杆机构

三连杆机构包括大臂、小臂和铲斗。由式（26）可得，大臂势能为G8h8，小臂势能为G5h5，铲斗势能为G1h1。

三连杆机构总势能为

三连杆机构总动能为

（2）液压缸-连杆机构

连杆一势能为G2h2，连杆二势能为G3h3，大臂液压缸势能为G7h7，小臂液压缸势能为G6h6，铲斗液压缸势能为G4h4。

液压缸-连杆机构总势能为

液压缸—连杆机构总动能为

系统总动能与系统总势能之差

式中：L为拉格朗日函数；T为系统总动能，V为系统总势能，。

依据拉格朗日方程可得

式中：jψ为关节变量的广义坐标；jψ˙为关节变量的广义坐标速度;jτ为三连杆机构关节驱动力矩，j=1,2,3。

对于井下水仓清挖机构构件j的势能求导得到液压缸-连杆机构关节驱动力矩

式中：'jτ为液压缸-连杆机构的关节驱动力矩；Vj为杆件j所对应的对驱动力矩作用的势能。

因此，井下水仓清挖机构的总关节驱动力矩为

3.2 液压缸驱动力仿真分析

运动学仿真结束后在齿尖位置添加切向力，以模拟挖掘阻力，并利用ADAMS对井下水仓清挖机构进行动力学仿真。由于运动学仿真时简化了对称分布的液压缸，所以仿真得到的液压缸驱动力数值为合力的数值结果。用数学方法求得单组液压缸的驱动力，得到的每个液压缸的驱动力见图14。

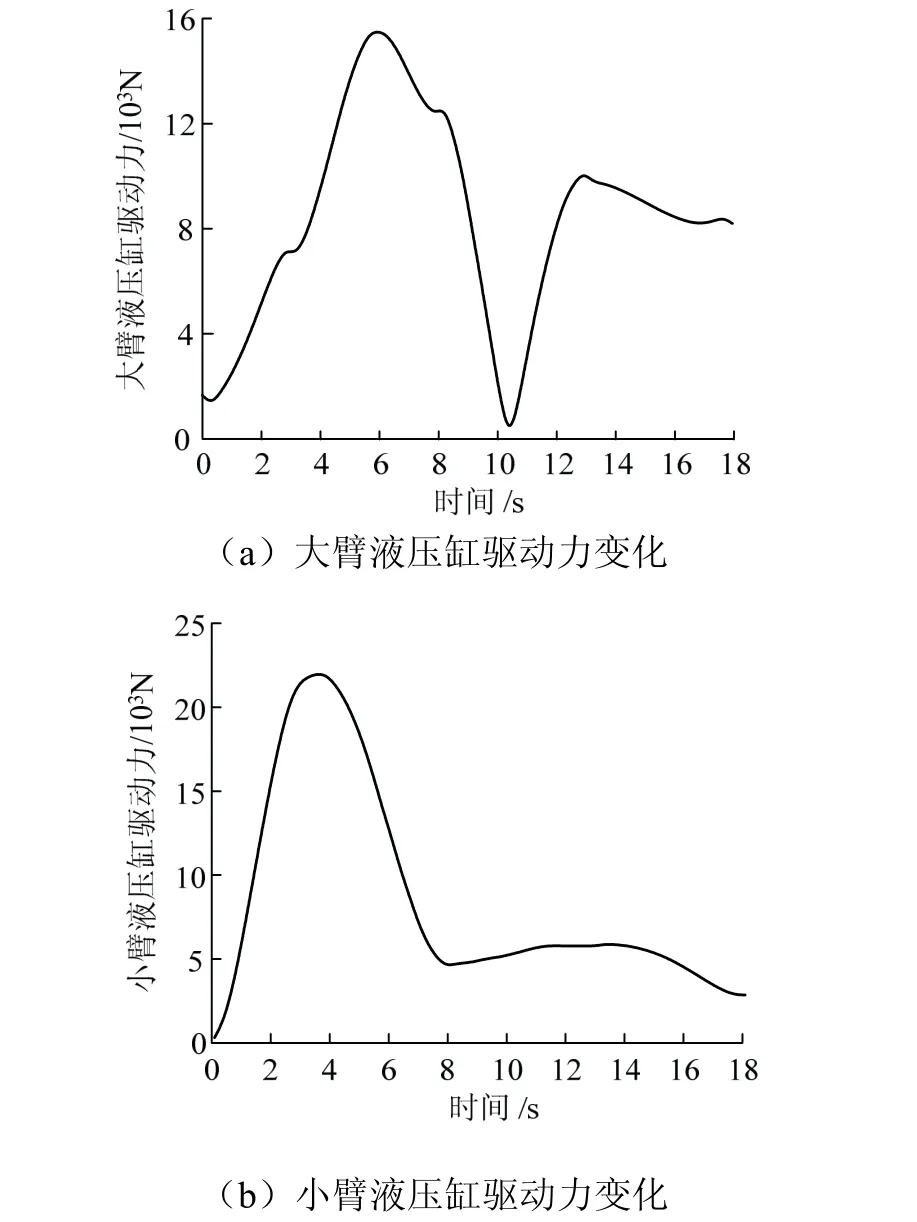
图14 液压缸驱动力Fig.14 driving force of hydraulic cylinder

液压缸驱动力具体变化如下。

（1）水平推铲阶段：在前3 s时段，大臂、小臂、铲斗液压缸的驱动力一直呈快速上升趋势，在第3 s时铲斗液压缸达到最大驱动力。

（2）铲挖阶段：在3～8 s时段，大臂、小臂的驱动力呈先增大后减小趋势，铲斗液压缸驱动力先快速减小后又略有增加，大臂液压缸驱动力在6 s左右达到最大，小臂液压缸最大驱动力在3.8 s左右达到。

（3）平移提升阶段：在8～13 s时段，大臂液压缸驱动力先快速减小后又快速增加，小臂液压缸驱动力略有增加，铲斗液压缸驱动力一直呈减小趋势。

（4）卸料阶段：在13～18 s时段，随着时间的增加大，臂和小臂液压缸的驱动力略有减小，铲斗液压缸的驱动力呈“W”形变化。

3.3 铰点受力仿真分析

选取井下水仓清挖机构组成构件的三个主要连接点进行仿真分析，各铰点受力情况见图15。

图15 主要铰点受力Fig.15 stress of main hinge points

从图15中可以看出，大臂-安装座铰点A处受力随着时间的增加先增大后减小，在5 s左右达到最大值。小臂-大臂铰点E处受力随着时间的增加先快速增大后快速减小，然后进入先缓慢增加后缓慢减小阶段，铰点受力最大值出现在3 s左右。铲斗-小臂铰点J处受力变化趋势与小臂-大臂铰点E处受力变化趋势相似，铰点受力最大值同样出现在3 s左右。铰点受力最大位置为铲斗-小臂铰点J。

4 结论

（1）研究了一种井下水仓清挖机构，建立了井下水仓清挖机构运动学模型，利用仿真数据与理论计算值进行对比，验证了所建立的运动学模型的正确性。

（2）基于建立的井下水仓清挖机构运动学仿真模型，得到了铲斗末端位姿变化曲线，表明井下水仓清挖机构移动轨迹具有连续性和平稳性，证明了该井下水仓清挖机构满足实际要求。

（3）通过对该井下水仓清挖机构进行ADAMS动力学仿真，得到了井下水仓清挖机构主要构件在工作过程中的受力特性，为进一步研究其清挖煤泥的性能及机构的优化奠定了基础。