基于改进入侵杂草算法的空调送风温度控制

杨世忠，逄 铄

（青岛理工大学 信息与控制工程学院，山东 青岛 266520）

0 引言

随着经济的快速发展，变风量空调在人们生活中愈加常见，同时对空调控制性能提出更高的要求，目前，实际应用最广泛的仍然是PID控制[1]，但由于变风量空调送风温度控制具有时变性和滞后性，传统PID控制已经很难满足精度和稳定性的需求。近年来专家们运用智能算法来对PID参数进行自整定，如粒子群算法（particle swarm optimization，PSO）、遗传算法（genetic algorithm，GA）。

萤火虫群算法（glowworm swarm optimization，GSO）[2]具有寻优速度快、搜索范围广等优点，因此被广泛用于多目标寻优，但萤火虫群算法搜索速度较慢，后期容易出现局部最优的问题，因此需要对基本GSO算法进行改进。李萍等[3]将改进萤火虫算法应用于SVR空气污染物浓度预测中，使预测精度有较大提升。周国光等[4]将萤火虫算法与神经网络结合，实现对气浮台自动调平衡的优化。于德鳌等[5]对萤火虫算法的固定步长进行优化，提出一种可变步长的萤火虫算法，并成功应用于风电系统的环境经济调度方面。ZHOU等[6]将改进萤火虫算法应用于人脸识别，发现识别率高于其他算法。范江波等[7]将萤火虫算法进行改进，引入了Pareto非支配解的更新机制，成功应用到机器人的多目标路径规划中。

本文在基本萤火虫群算法的基础上，提出一种入侵杂草优化萤火虫算法（invasive weed optimization glowworm swarm optimization，IWO-GSO），解决萤火虫群算法由于初始位置较差，容易造成局部最优和搜索时间过长的问题。

1 被控对象数学模型的建立

1.1 变风量空调送风温度-冷冻水阀结构

为保持冷冻水系统送风温度稳定，变风量空调需要根据房间负荷需求调节末端装置的送风量。但在实际空调系统运行中，送风温度在设定值不断发生变化，因此，有必要对送风温度进行控制，使系统在节能的同时兼顾控制的稳定性和精确性[8-9]，从而获得更优的控制效果。空调水系统示意见图1。由图1可知，传感器检测到送风温度实际值，与上位机送风温度设定值进行对比，根据对比结果调节冷冻水阀开度，从而调节冷冻水的流量，使送风温度达到设定值并保持稳定。

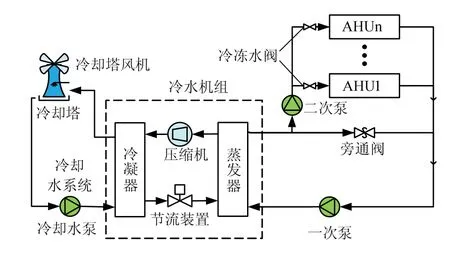
图1 水系统结构示意Fig.1 structural diagram of laboratory water system

1.2 建立系统数学模型

通过系统辨识的方法确定系统的数学模型。主要分为如下步骤。

步骤1确定过渡时间Ts。使空气处理机组冷冻水阀门开度的M序列幅值保持在5%～10%，给冷冻水阀开度一个阶跃信号并观察其静态特性。将冷冻水阀开度控制在5%，待送风温度达到稳定状态后，再给冷冻水阀门一个5%的阶跃信号，同时观察冷冻水阀门开度发生变化后的送风温度波动范围。经过多次试验得到过渡时间Ts约为800 s，延迟时间τ约为50 s。

步骤2求解系统的截止频率f。在保证M序列幅值不变的情况下，将不同频率的正弦波载入至控制回路，观察输出是否能跟随输入变化[10]。如果系统的频率变为某个固定值，同时输出幅值小于系统初始幅值的5%，那么此频率就是要求的截止频率，本次试验求得截止频率为0.005 Hz。

步骤3确定采样周期Np。M序列是一种随机序列，周期为T=NpΔt，Np为M序列周期长度，Δt为M序列采样时间，根据f，f为截止频率，可求Δt≤66.7，因此取整可得Δt=60，根据，可求得Np＞14.3，取整可得Np=15，再由Np=2n-1可得n为4，可知M序列为4级反馈移位寄存器产生。

经过系统辨识，并且对拟合出的模型进行处理，得到送风温度-冷冻水阀的传递函数为

由于送风温度控制具有大滞后性和时变性，因此运用传统PID控制很难达到令人满意的控制效果，本文选择改进后的IWO-GSO算法对PID控制进行优化，从而提高系统的控制效果。

2 优化控制算法设计

2.1 基本萤火虫算法

萤火虫群算法是一种群智能优化算法，它将萤火虫之间的相互吸引和移动过程应用在算法的搜索以及寻优过程，通过对目标函数的求解，从而判断萤火虫所处位置的优劣[11]。在萤火虫群算法中，每个萤火虫都均匀分布在D维目标函数搜索空间中，每只萤火虫都携有荧光素li并且拥有各自的决策半径Rdi，萤火虫的亮度与该萤火虫所在位置的目标函数值有关，亮度越大说明萤火虫在此处具有越好的目标函数值，反之则具有较差目标函数值。如果一只萤火虫i邻域内萤火虫数目越多，则萤火虫i的决策半径越小，反之萤火虫数目越少，决策半径越大。最终，大部分萤火虫会聚集在多个较好的目标函数位置[12]。萤火虫决策半径更新可表示为

式中：Rdi(t+1)为第i只萤火虫在第t+1代时的决策半径；Rs为萤火虫感知半径；β为决策半径更新系数；ni为萤火虫周围邻居的阈值；Ni(t)为邻域集合，为

式中，rij(t)为第t代萤火虫i和j之间的欧氏距离。

荧光素更新为

式中：li(t+1)为第t+1代萤火虫i所含荧光素值；ρ为荧光素的挥发因子；γ为荧光素更新速率；f(xi(t+1))为萤火虫i在t+1次迭代时所对应的目标函数值。

萤火虫i向在邻域集Ni(t)内萤火虫个体j移动的概率，为

萤火虫位置更新可表示为

式中：xi(t)为萤火虫i在第t次迭代时的位置；L为萤火虫i的移动步长。

2.2 入侵杂草优化算法

入侵杂草优化算法是Mehrabian等[13-14]提出一种模拟杂草繁殖的算法，该算法是模拟杂草种子的生成、扩散和繁殖以及适者生存的自然过程，具有良好的收敛性、鲁棒性和强随机性。算法运行原理为，在初始区域随机初始化一片杂草，算法运行的过程中，杂草产生的种子与其适应度成比例。杂草种子数目与适应度函数之间的关系为

式中：Pi为杂草种子的数；fi为杂草的适应度函数；Pmax和Pmin为种子数的最大值和最小值。

确定杂草种子数的原理见图2。

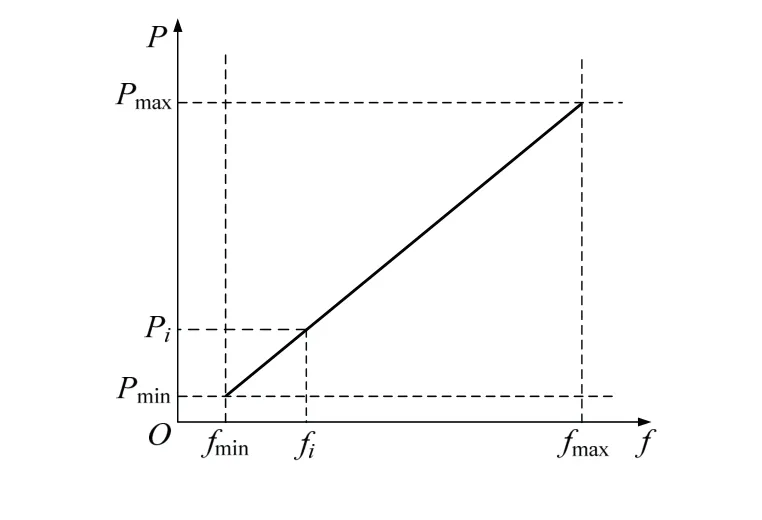
图2 确定杂草种子数Fig.2 determine the number of weed seeds

从图2中可知，杂草种子数与适应度有关，适应度越高，产生的种子越多，适应度越低，产生的种子越少。初始随机生成的种子在搜索空间中以正态分布分散在母株的周围，正态分布比标准偏差为

式中：σq为正态分布的标准偏差；q为当前杂草种群迭代次数；qmax为最大杂草种群迭代次数；σini为初始标准偏差；σfin为最终标准偏差。

式（8）确保了标准偏差分布是从初始值减小到最终值。经过多次迭代，种群数达到最大值，此时引入竞争过程，适者生存。将母株和子株根据适应度值按大小顺序排列，种群数目最大时，剩余植株被淘汰。

2.3 IWO-GSO算法

在基本GSO算法中，如果要优化的区域较广，那么初始化的萤火虫位置会更加分散，并且由于萤火虫亮度不足，所以无法进行单个萤火虫的搜索。空间中会出现很多单独分散的萤火虫从而导致资源的浪费，这会降低算法运行的效率，从而导致局部最优的问题。同时萤火虫目标选择和运动具有随机性，位置不断更新，萤火虫与最优值之间的距离无法精确。在算法运行时，如果步长太大，萤火虫会移动的很远，那么萤火虫个体会超过最佳位置。如果步长太小，迭代次数会增加，导致收敛速度过慢、鲁棒性较差。

因此，引入入侵杂草优化算法，入侵杂草优化算法中后代个体正态分布标准差σq为后代萤火虫的分布步长，σq更新见式（8），可知母体萤火虫产生的后代的分布步长σq会随着迭代次数的增加而减小，算法前期进行大规模搜索，后期进行小规模搜索，这增强了算法的局部搜索能力。根据目标函数值对所有个体进行排序，设置阈值δ，将低于该阈值的个体替换为高于该阈值的个体并进行下一次迭代；排序后，记录最佳个体的位置和目标函数值。每次迭代后，计算每个萤火虫的目标函数值，并与记录的最佳目标函数值进行对比。如果目标函数值优于记录值，则替换，如果低于记录值，则保持不变；最后使用记录的最佳目标函数值更新萤火虫的决策半径Rdi(t+1)和移动步长L。在IWO算法与GSO算法结合的过程中，需要选择合适的初始标准偏差σini、最终标准偏差σfin和阈值δ。利用测试函数进行参数测试，测试函数为

经过测试，当σini=1.5、σfin=0.5、δ=0.45时IWO-GSO算法寻优能力最佳，部分测试结果见表1。

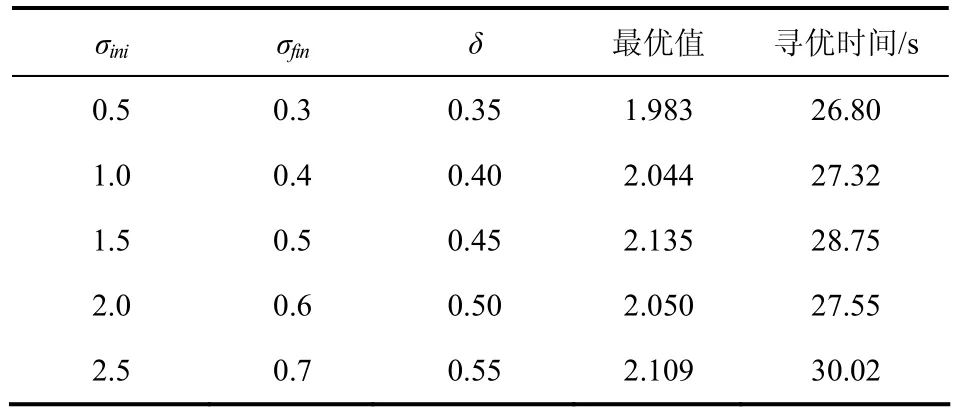
表1 实验参数选择对比Tab.1 comparison of experimental parameter selection

优化后的IWO-GSO算法可以有效解决GSO算法收敛速度慢、容易陷入局部最优的问题，算法流程见图3。

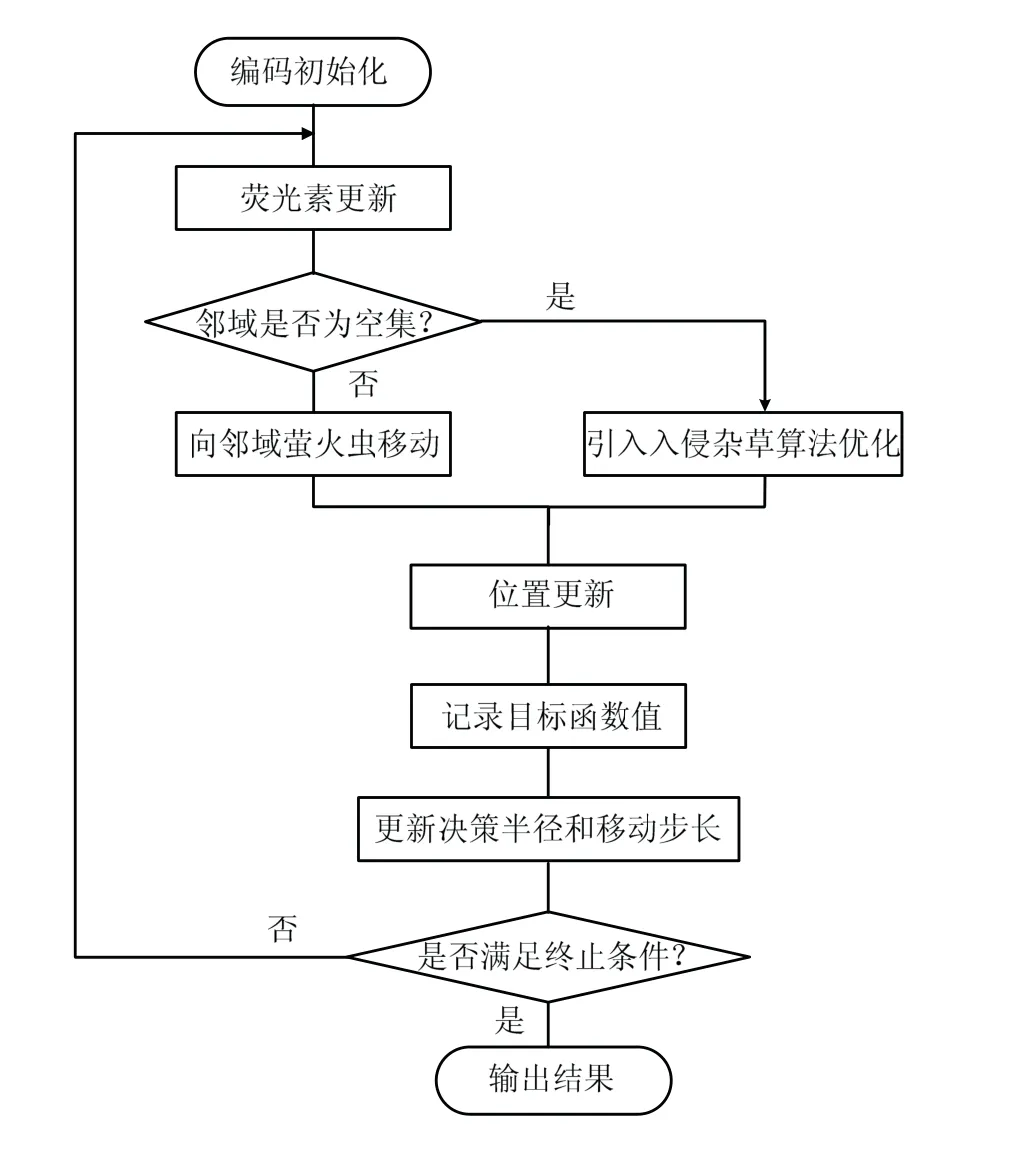
图3 IWO-GSO算法流程Fig.3 IWO-GSO algorithm flow chart

2.4 IWO-GSO优化PID控制

根据IWO-GSO算法对PID控制进行优化，首先要选择合适的适应度函数，本文选用常规PID参数整定性能指标ITAE[15-16]，ITAE可表示为

式中，e(t)为峰值误差。

对ITAE指标进行离散化，设T=ntΔ，可得适应度函数为

式中，t(i)=iΔt。

ISO-GSO优化的PID控制原理见图4。

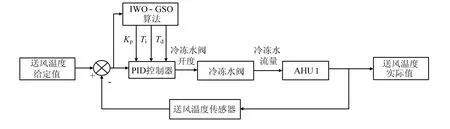
图4 IWO-GSO算法优化PID控制原理Fig.4 IWO-GSO algorithm optimized PID control schematic diagram

3 仿真及实验验证

3.1 Matlab仿真验证

利用Matlab对改进后的IWO-GSO算法进行效果验证，设置最大迭代次数tmax为100，萤火虫种群规模为50，荧光素浓度l0为5，荧光素挥发因子ρ为0.4，初始感知半径Rs为2.5，初始决策半径Rdi为2.5，步长L为0.2。

由于实验工况为夏季，因此送风温度设为13℃、14 ℃和15 ℃。基本GSO算法与IWO-GSO算法的训练误差对比见图5，图6，GSO优化PID、IWO-GSO优化PID、GA优化PID仿真对比见图7。

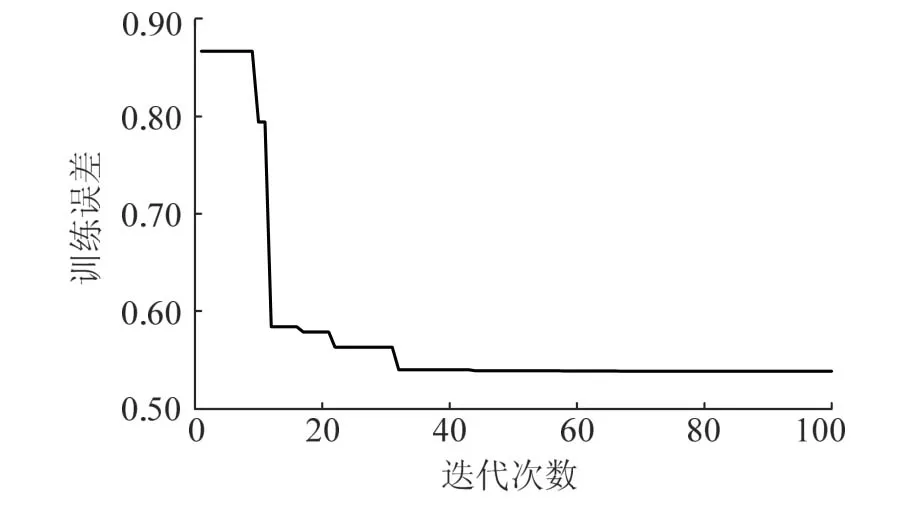
图5 GSO算法的训练误差Fig.5 training error of GSO algorithm

图6 IWO-GSO算法的训练误差Fig.6 training error of IWO-GSO algorithm

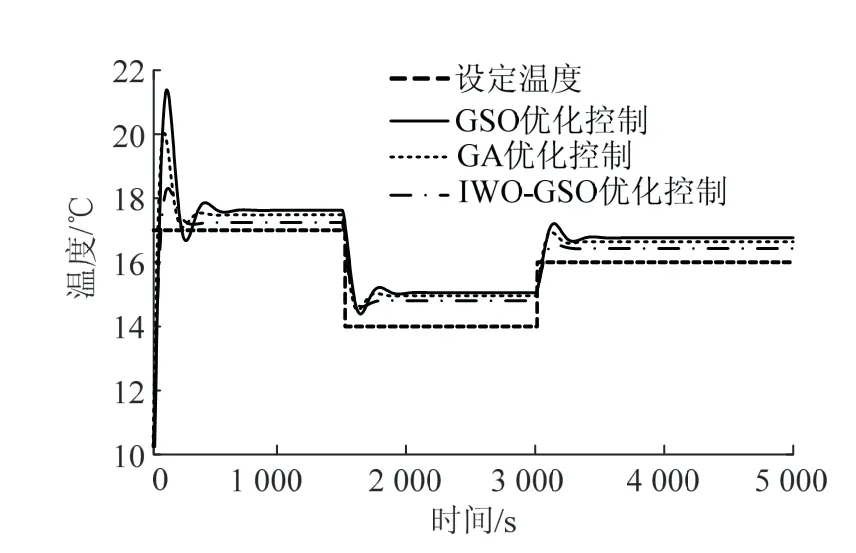
图7 各算法优化PID仿真曲线对比Fig.7 comparison of PID simulation curves for each algorithm optimization

基本GSO和IWO-GSO控制器仿真VAV空调系统送风温度控制效果动态性能指标对比见表2。

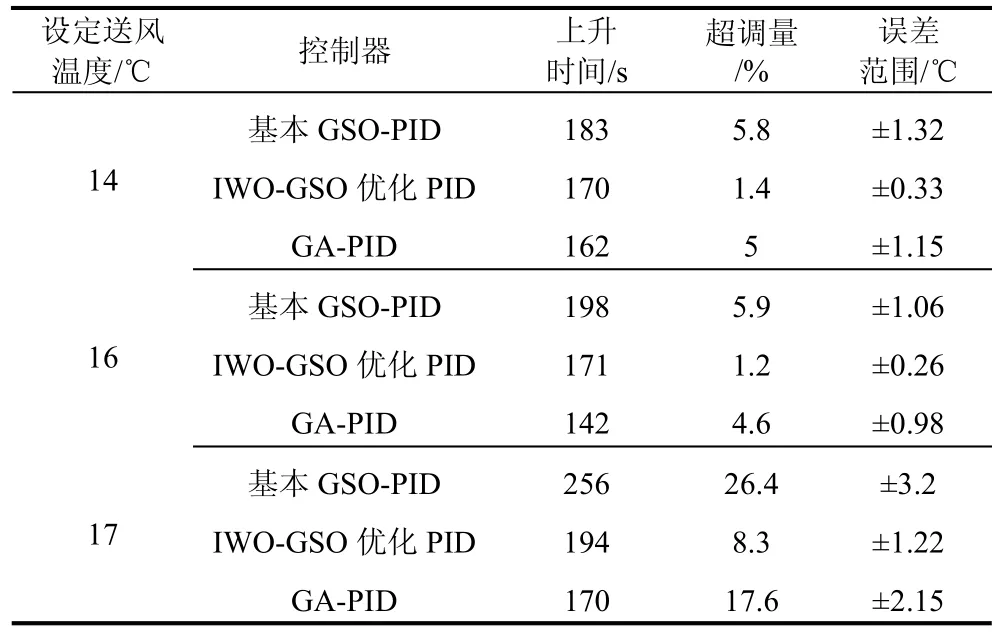
表2 仿真控制动态性能比较Tab.2 comparison of dynamic performance of simulation control

由图5、图6可见，IWO-GSO算法比GSO算法的训练误差有所下降，达到稳定时的迭代次数也有所减少，根据图7和表2的对比可以看出，IWO-GSO算法虽然比GA算法优化时间长，但系统超调量和误差明显下降，因此，本文提出的控制方法可以有效改善控制效果。

3.2 变风量空调实验验证

将基本GSO-PID和IWO-GSO优化PID控制应用到青岛理工大学变风量空调控制系统中，将传感器数据作为节点，通过监测送风温度，在夏季运行的情况下，设定送风温度为17 ℃、14 ℃、16 ℃，冷冻水阀门开度设定为5%。经过1 h的预处理后开始实验，实验时间为6000 s。送风温度实测值见图8～图10，为了更加明显地验证能耗情况，每30 min测量一次能耗，取10：00—13:00的7个时间点进行能耗统计，能耗对比见图11，控制系统动态性能对比见表3。

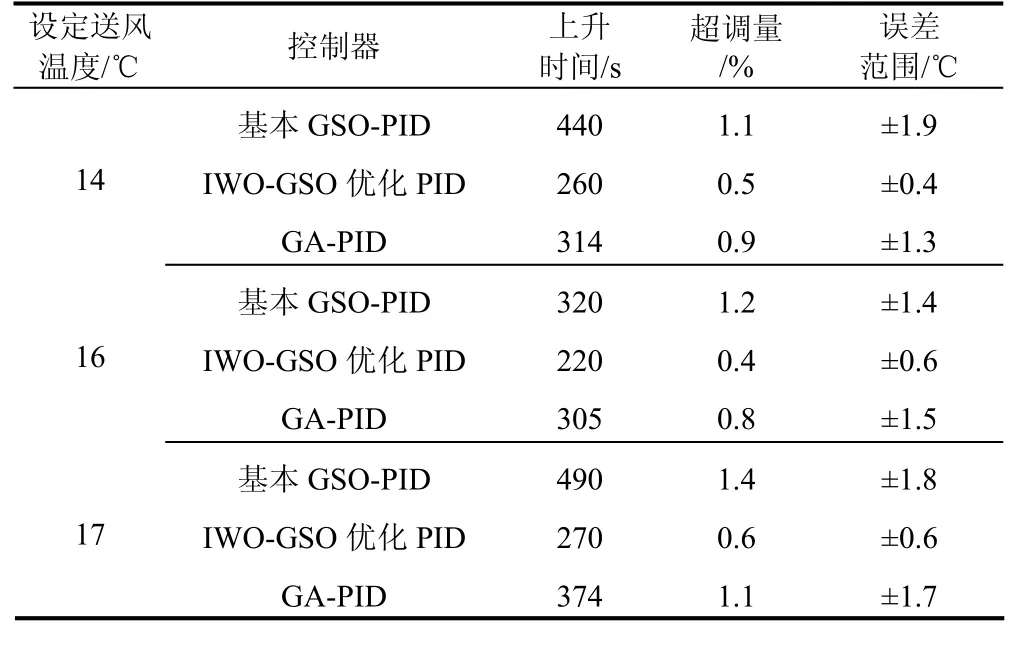
表3 控制系统动态性能比较Tab.3 comparison of dynamic performance of control systems

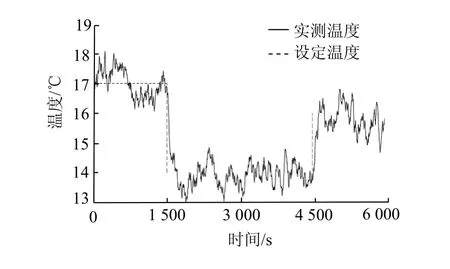
图8 基本GSO优化PID控制送风温度Fig.8 basic GSO optimized PID control of air supply temperature

图9 GA优化PID控制送风温度Fig.9 GA optimized PID control of air supply temperature

图10 IWO-GSO优化PID控制送风温度Fig.10 IWO-GSO optimized PID control of air supply temperature

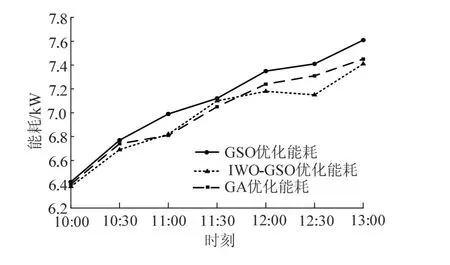
图11 能耗对比Fig.11 comparison diagram of energy consumption

由图8～图10和表3可知，IWO-GSO优化控制效果明显优于基本GSO优化控制和GA优化控制，其超调量较小，动态特性较好，温度误差波动范围较小，具有较强的鲁棒性。由图11可以看出，在实验的3 h内，与未改进的系统相比，改进后的系统能耗有所降低，说明该控制策略具有一定的节能效果。

4 结论

（1）根据变风量空调送风温度-冷冻水阀系统的特点，提出一种IWO-GSO优化控制，将入侵杂草优化算法与萤火虫群算法相结合，有效改善了传统PID控制存在的弊端，以及基本萤火虫群算法后期容易陷入震荡、局部最优和收敛速度较慢的问题。

（2）仿真结果表明，与基本GSO优化控制和GA优化控制相比，变风量空调送风温度-冷冻水阀系统的IWO-GSO优化控制使系统的超调量和稳定时间减少。实验证明改进后的控制方法能有效克服送风温度控制中的不确定性和扰动，系统能耗有所降低。该策略可为空调送风温度控制的工程应用提供一定参考。