新型高增益开关电容Zeta式DC-DC变换器

杨子鑫，陈忠华

（辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105）

0 引言

目前，光伏发电是最具可持续发展特征的新型绿色能源之一。由于光伏电池板输出电压较低，不能直接应用到并网逆变器直流负载。因此，需要利用DC-DC变换器将较低的电压升高，提高传统DC-DC变换器的电压增益成为近几年研究热点[1-2]。

传统Boost变换器的电压增益与占空比成正比，但高占空比会导致变换器的效率降低，同时功率器件的输出电压应力也会增加。文献[3]、文献[4]通过加入开关电容提升电压增益，但元器件数量的增多使变换器的导通损耗增加，而且存在电容充放电时电流较大的问题。文献[5]～文献[7]加入耦合电感倍压结构，利用副边给倍压电容储能，不仅减小了电容储能时的电流冲击，又改善了电压增益。文献[8]～文献[12]将耦合电感与倍压电容组合，把电容-二极管支路既当做钳位吸收支路，减小开关管电压应力，又做电容倍压支路，提升变换器电压增益。

本文提出一种高增益Zeta变换器，通过调节耦合电感的匝比N提升变换器的电压增益。同时将开关电容中的电容-二极管结构当做钳位支路吸收耦合电感的漏感能量，以此降低寄生电容储能时的电流冲击，减小开关管的电压应力，提高变换器的转换效率。

1 高增益开关电容Zeta变换器构成

通过等效变换Zeta变换器中的二极管-电容结构（diode-capacitor multiplier，DCM），得到等效Zeta变换器，再将两变换器中的DCM结构进行组合，形成开关电容结构，即得到开关电容Zeta变换器。将耦合电感原边作为开关电容Zeta变换器的前级电感，副边与DCM组成耦合电感倍压单元，再与其进行并联，构成新型高增益开关电容Zeta式DC-DC变换器。该变换器中，开关电容的两个DCM单元不仅作为钳位吸收支路，吸收耦合电感的漏感能量，还作为电压提升支路。变换器拓扑演变过程见图1。

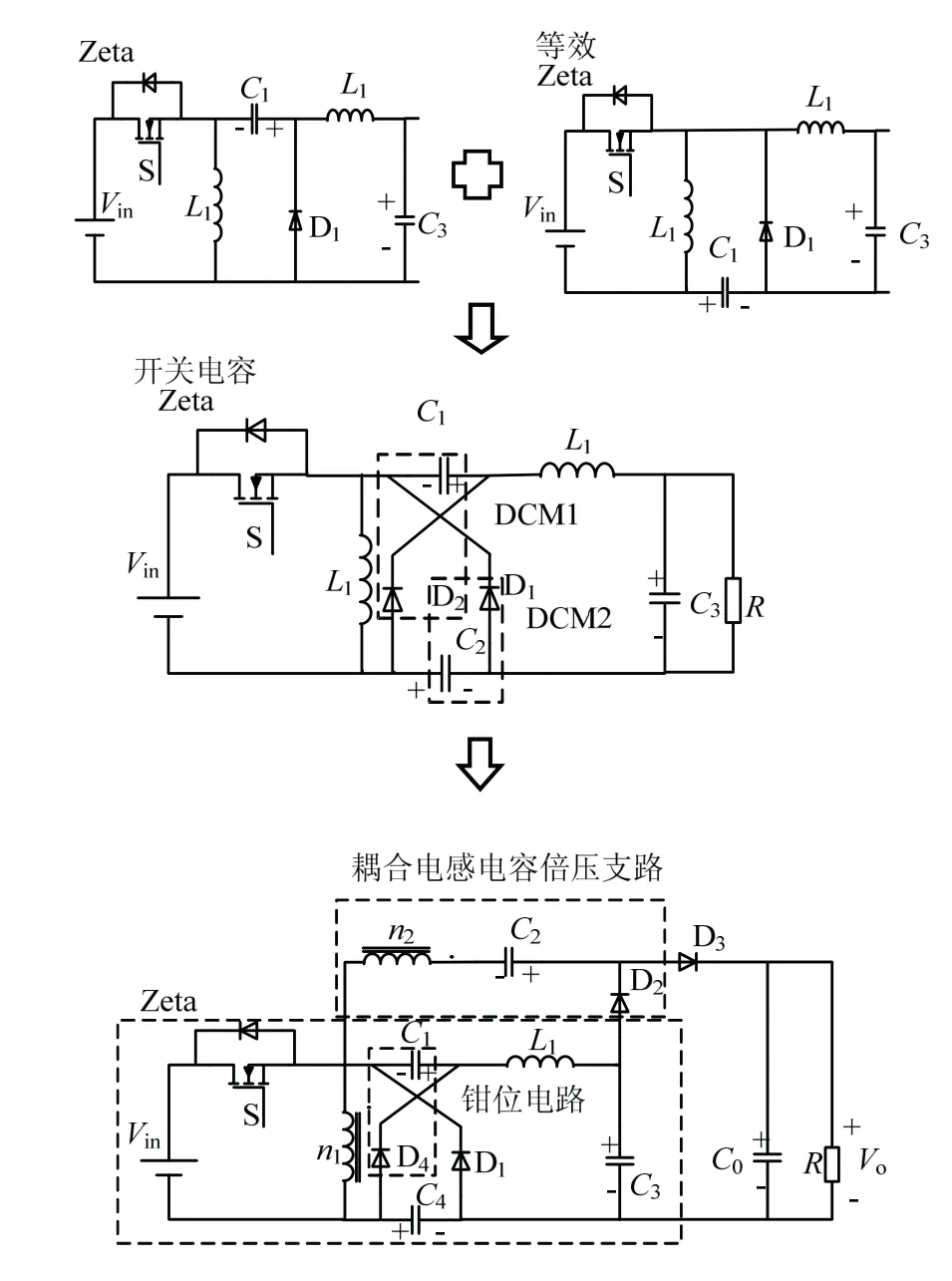
图1 变换器拓扑结构变换Fig.1 topology transformation of converter

2 工作原理

2.1 变换器等效电路

变换器等效电路见图2。

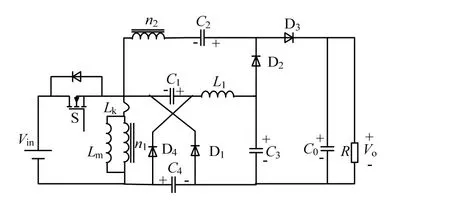
图2 等效电路Fig.2 equivalent circuit

为便于分析变换器的工作原理，假设：①所有电容足够大，忽略纹波效应；②耦合电感的耦合系数k=Lm/(Lm+Lk)，Lm为励磁电感，Lk为漏感；③电路中各个元器件均为理想器件。

2.2 变换器模态分析

连续工作模式下，变换器一个循环周期内有5种工作形态。变换器主要波形见图3，5种工作模态等效电路见图4。

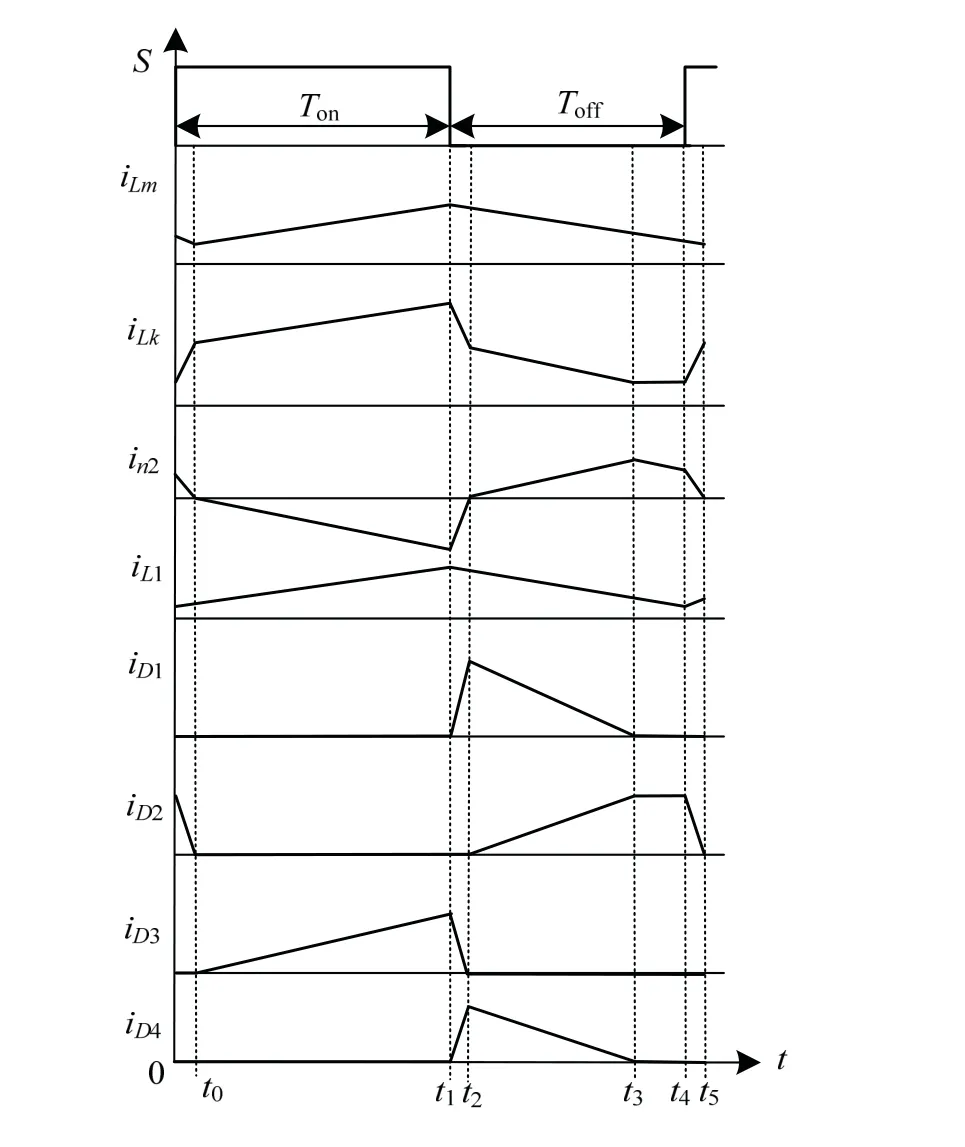
图3 变换器主要参量工作波形Fig.3 main parameters of the converter working waveform

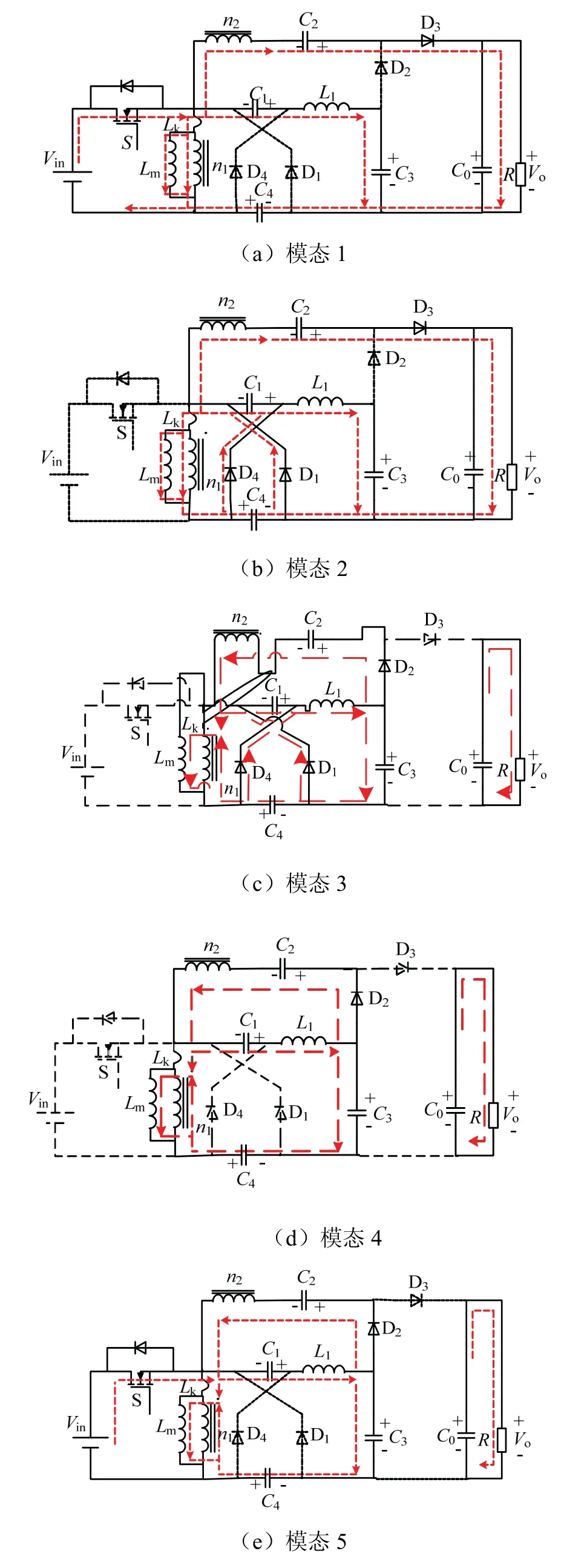
图4 变换器工作模态等效电路Fig.4 equivalent circuit of converter operating mode

模态1[t0，t1]：开关管S以及二极管D3导通；输入电源Vin给励磁电感Lm与漏感Lk提供能量，励磁绕组中的能量借助副边绕组n2与电容C2给负载与电容C0供电；同时，电源Vin与电容C1串联给电感L1进行能量的存储；iD3从t0时刻开始呈线性增加，二极管D3导通。此模态电流iLm、iLk分别为

模态2[t1，t2]：漏感能量由二极管D1与D4向电容C1、C4转移，因为漏感Lk较小，iLk迅速下降；同时，电感L1向电容C3充电；在t2时刻，副边绕组电流逐步减小至0，二极管D3关断，此模态结束。此模态电流iLm、iLk分别为

模态3 [t2，t3]：电感L1的能量通过二极管D4向电容C3、C4转移，电感L1的电流iL1逐渐减小；励磁绕组的能量经由耦合电感的副边绕组n2向电容C2充电，电感的电流in2逐步线性上升；在放电过程中，iLm、iLk不断减小，在t3时刻，iD1、iD4下降至0，此模态结束。此模态电流iLm、iLk分别为

模态4 [t3，t4]：仅二极管D2导通；励磁电感Lm和电容C1、电感L1串联向电容C3、C4充电，通过励磁电感电流iLm持续减小。此模态电流iLm、iLk分别为

模态5[t4，t5]：电源Vin连同电容C1、C3、C4为电感L1储能，电流iL1线性增大；在t5时刻，副边绕组电流下降至0，同时二极管D2关断，此模态时间较短暂。此模态电流iLm、iLk分别为

3 变换器工作性能分析

3.1 电压增益分析

为便于稳态分析，只考虑模态1和模态3。

当变换器工作在模态1时，由图4（a）可得

当变换器工作在模态3时，由图4（c）可得

基于电感平衡原理得出

由式（19）、式（20）可得电容的电压为

将式（21）～式（23）代入（14）得到变压器在理想情况下的电压增益为

D为0.6时，电压增益与匝比N、耦合系数k的关系见图5。由图5可见，匝比N不变时，输出增益随k增大而增大，反之，输出增益随k减小而减小。因此，在设计变换器时，耦合电感应尽量做到紧耦合。

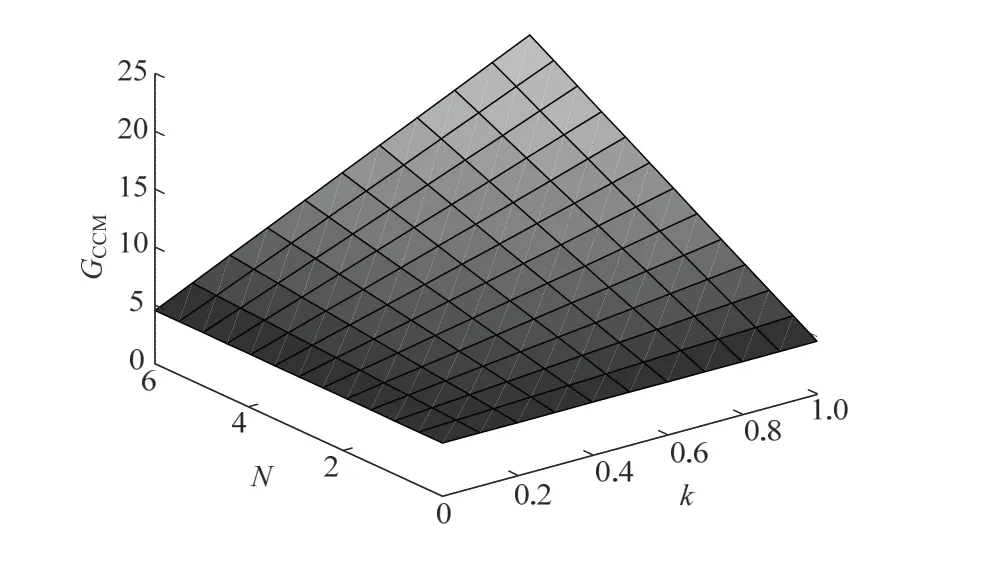
图5 电压增益GCCM与匝比N、耦合系数k的关系（D=0.6）Fig.5 relationship between voltage gain GCCM and turn ratio N，coupling coefficient k (D=0.6)

3.2 占空比丢失

受漏感的影响，变换器的增压效果通常都低于理想情况。为便于理解，忽略模态2和模态5，假设漏感和电容C1、C2的谐振周期很大，故漏感电流可为直线。图6为简化工作波形，其中ILm、IL1分别为励磁电感Lm、L1的平均电流，NIoT为时间DT内漏感增加的电量，IoT为T14时间内通过二极管D1的电量。T14为t1时刻到t4时刻的时间段。

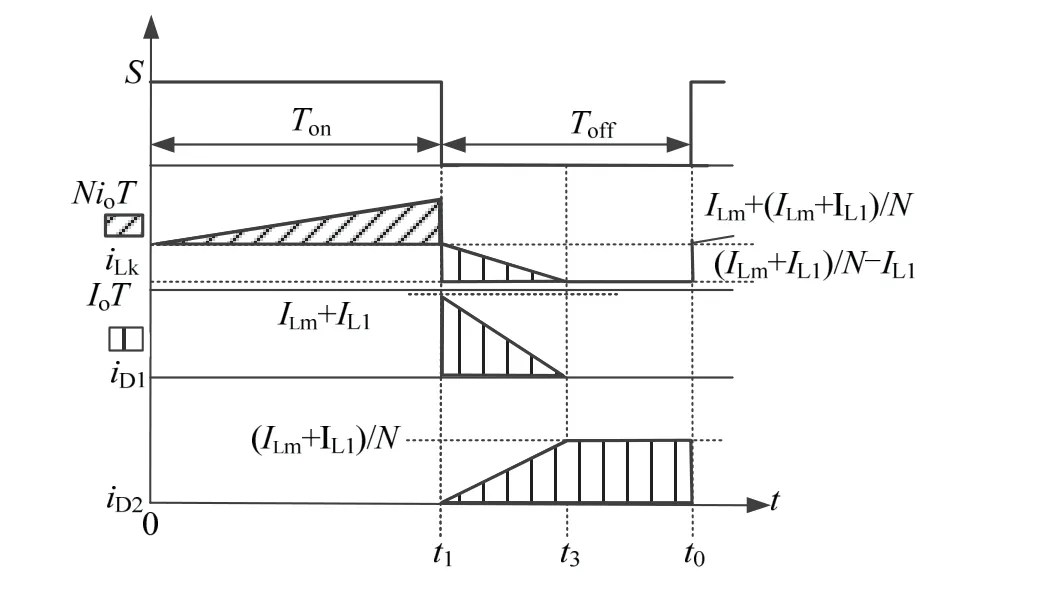
图6 简化工作波形Fig.6 simplified working waveform

由于在每个周期内，流经二极管的平均电流与输出电流相等，故而单位周期内二极管的电量均为IoT。

利用二极管D1、D2电量相等的关系，可以求出T13和T30。

设耦合电感原边电压为Vy，在T13时间段有

在T30时间段内有

在T01时间段内有

综上可得

令km=Lkfs/R，得到实际电压增益为

实际电压增益与漏感的关系见图7。

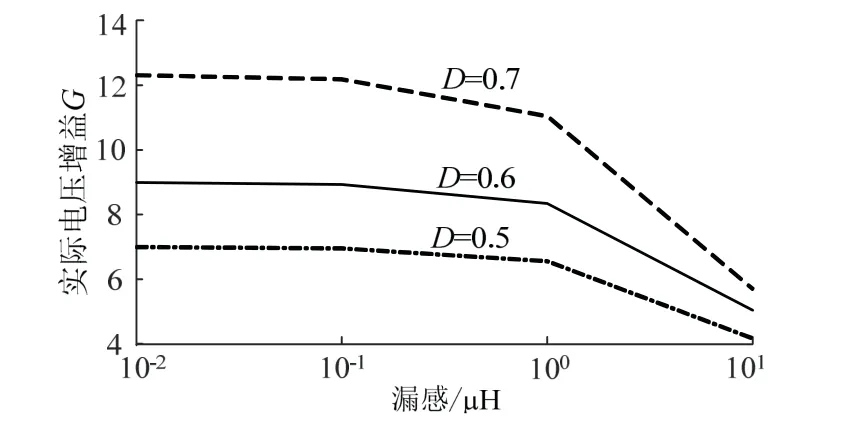
图7 实际电压增益与漏感的关系Fig.7 actual voltage gain connection with leakage inductance

由图7可知，占空比越大，实际增益越大，随漏感的增加，实际增益减小，同时漏感值较大时会导致占空比丢失，影响变换器性能，因此在实验时要尽量做到紧耦合，即耦合系数接近于1。

3.3 电压应力分析

令耦合系数k=1，得到电容C1、C2、C3、C4的电压应力为

功率器件的电压应力为

电压应力与匝比N的关系见图8。

图8 电压应力与匝比N的关系Fig.8 voltage stress and turn ratio

从图8中可知，增加匝比N，开关管S、二极管D1、D4的电压应力逐渐降低，但二极管D2、D3应力却在增加，故而在设计变换器耦合电感匝比时应考虑各个器件应力情况。

4 变换器的性能对比

将本文所提出的新型高增益开关电容Zeta式变换器与基本Zeta变换器、磁集成Zeta变换器[13]、开关电感Zeta变换器[14]，以及磁集成Boost-Zeta组合变换器[15]的性能进行对比，表1为各个变换器的性能参数。

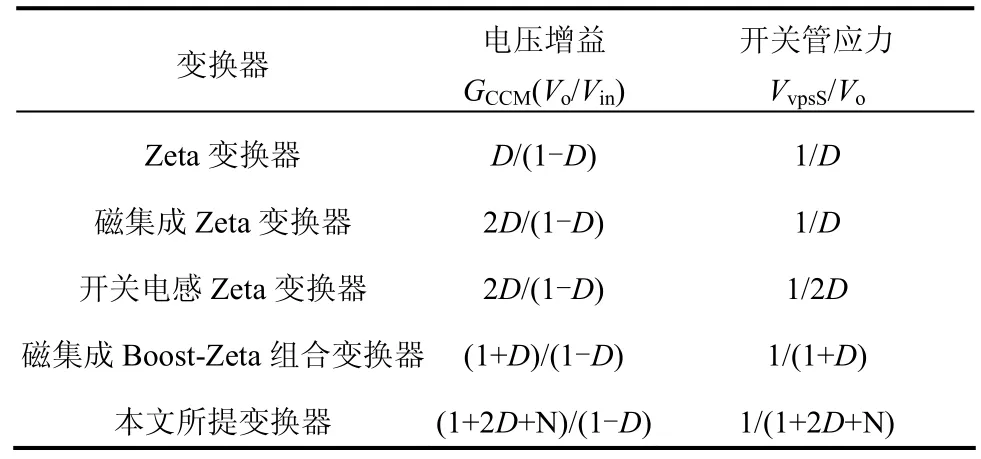
表1 变换器性能参数Tab.1 performance parameters of converter

当匝比N为2时，不同变换器电压增益与开关管应力对比见图9、图10。

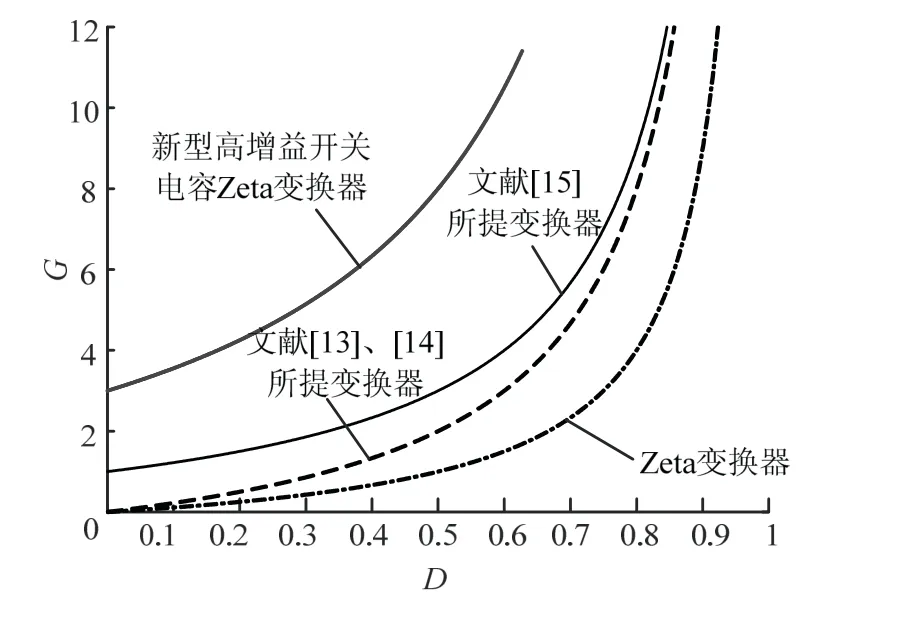
图9 电压增益对比Fig.9 comparison of voltage gain

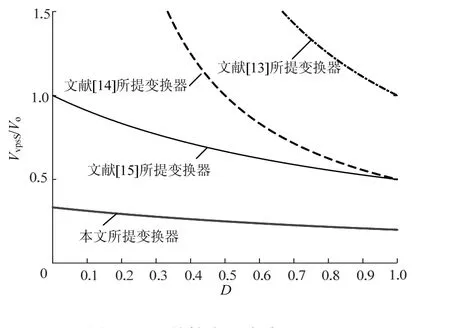
图10 开关管电压应力对比Fig.10 voltage stress comparison of switchgear

从图9可见，本文所提Zeta变换器的电压增益最高。从图10中可知，本文所提变换器的开关管电压应力明显小于其它变换器，因此，可采用低导通电阻、低电压等级的MOSFET搭建实验平台，有利于减少实验成本。

5 实验结果分析

为验证理论分析的正确性，搭建了一台150 W的实验样机，实验参数见表2，实验样机见图11。

表2 实验参数统计信息Tab.2 statistical information on experimental parameters

图11 实验样机Fig.11 test sample

图12 为变换器的输入输出电压，可见，电压由20 V提升到200 V。图13为漏感与副边的电流波形。图14为功率器件的电压、电流波形，其中开关管S的电压约为52 V，远小于Vo；二极管D1～D4具备零电流关断功能，证明理论分析的正确性和实用性。

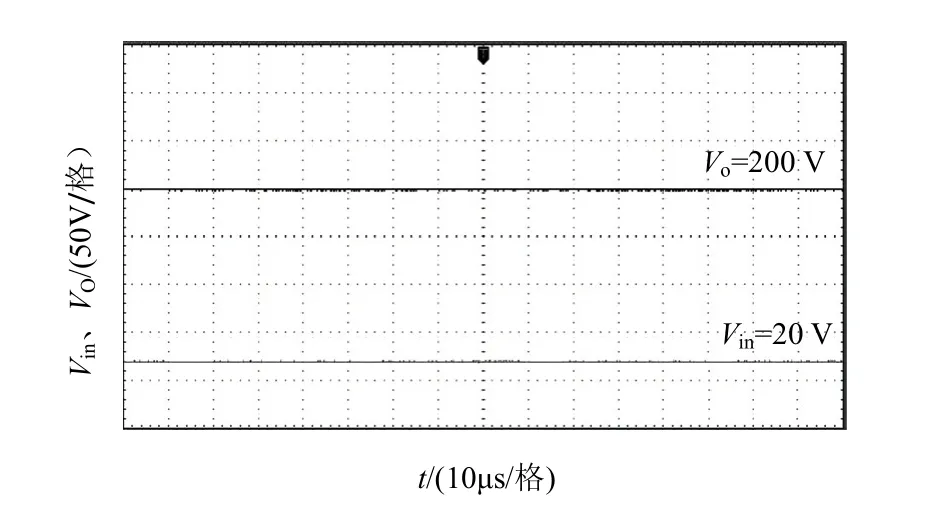
图12 输入输出电压波形Fig.12 Input-output voltage waveform

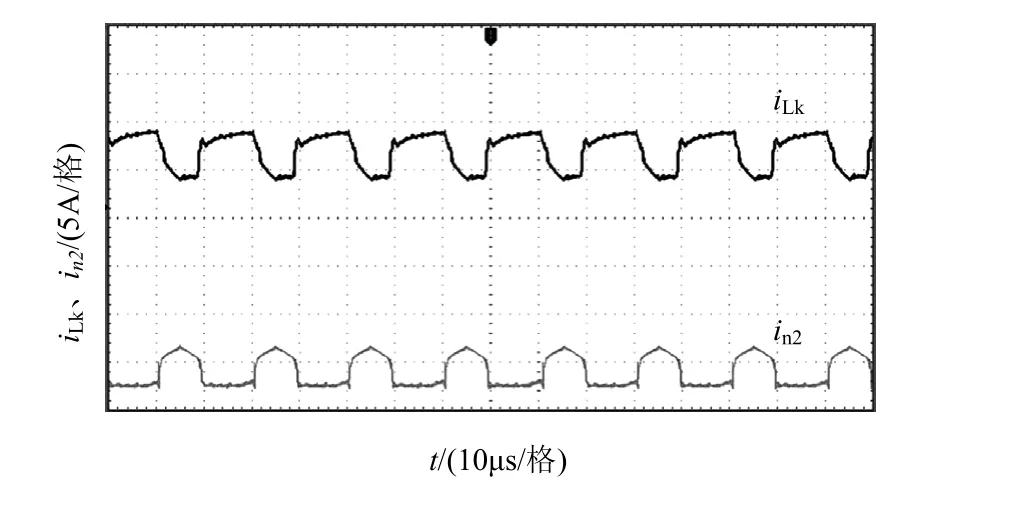
图13 漏感与副边电流波形Fig.13 leakage sense and secondary edge current

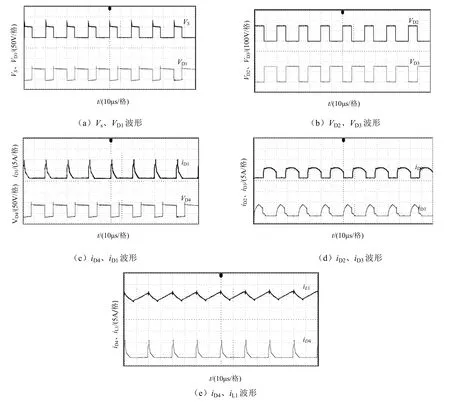
图14 功率器件的电压、电流的波形Fig.14 voltage and current of power device

该变换器在不同功率下的参考效率曲线见图15，变换器最高效率约为95.5%，额定功率时效率约为94.9%。由此可见，该变换器具有较高的效率可以满足光伏发电的要求。

图15 参考效率Fig.15 reference efficiency

5 结论

本文设计了一种新型高增益开关电容Zeta式变换器，分析了变换器在连续工作模式时的工作模态，给出性能指标数据，利用实验验证了理论分析的正确性，主要结论如下。

（1）把耦合电感和开关电容加入到Zeta变换器，利用提升耦合电感匝比进一步提高变换器的电压增益。

（2）由于输出电压远高于开关器件的电压应力，故可采用低导通电阻、低电压等级的开关器件，降低了导通损耗。

（3）利用开关电容中的二极管-电容支路即倍压钳位支路，控制了漏感谐振产生的电压尖峰，使变换器效率得到改善。