改进快速群搜索算法在配电网无功优化中的应用
单亚峰,杜天霖,金 岑,付 昱,徐 胜
(1. 辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105;2. 国网葫芦岛供电公司,辽宁 葫芦岛 125100)
0 引言
传统电力系统无功优化是指在满足约束条件下,通过调整配网中控制发电机及补偿电容器装置的无功出力,以及可调档变压器档位,达到有功损耗最小,提高电压总水平,对于保证电力系统的安全、稳定和高效率运行具有重大意义。电网的无功优化是一个多约束、多控制参数、离散参数和连续参数共存的非线性组合优化问题。智能优化算法在求解此类非线性组合优化问题的方面具有优势,常用算法包括经改进的遗传算法[1]、免疫算法[2]、自适应粒子群算法[3]、禁忌搜索法与其他混合算法[4]等。
文献[5]在基本粒子群(PSO)算法的基础上引入自适应权重和遗传算法,提出一种新型改进HPSO算法进行无功优化,但其收敛速度较慢。Barnard等提出的群搜索优化(group search optimizer,GSO)算法[6],其灵感来源于自然界中具有群居特性动物的搜寻食物行为,如鸟类、鱼类、狮子等。这种优化算法的优势在于考虑了群体中个体间的“相互合作”和“信息共享”的特性,群成员分别是发现者、加入者和游荡者。从文献[7]中可见,除发现者数目和搜索者比例外,其他参数对GSO基本上不存在干扰因素,这充分体现出GSO算法的鲁棒性。但该算法计算量大,收敛速度缓慢。文献[8]以分布式电源消纳最大、网损最低、电压偏差最小为目标,构建了主动配电网分区分布式优化控制模型,解决了配电网分区主动管理的边界耦合问题,降低了区域配电网的网络损耗。文献[9]在经典无功优化模型的基础上,建立最优无功优化模型,在建模过程中引入罚函数处理变量越界问题,并提出快速群搜索优化算法(fast group search optimizer,FGSO),应用标准IEEE30节点系统对该算法进行了验证。
1 无功优化数学模型的建立
无功优化问题[10]是影响电力系统经济运行特性主要因素之一,考虑其独有的多变量、多约束、非线性和变量种类混杂的特点[11],建立无功优化模型。选择电力系统的有功损耗值最小化为优化目标函数,为解决状态参数节点电压和发电机无功输出超边界的问题,引入惩罚因子,采用罚函数法进行处理。
1.1 无功优化目标函数
系统无功优化的目标函数为
式中:Gij为节点i和节点j间的支路电导;iV、Vj为节点i和j点间电压的模值;ijθ为节点i和节点j间的相位差;vλ为超出电压限制的惩罚因子;gλ为超出发电机无功输出的惩罚因子;集合P、G分别为超出限制条件的电压点集合和无功输出的点集合;Vi.lim和Ql.lim分别为i节点的电压和无功约束边界值,可以表示为
式(2)、式(3)中:Vi.max、Vi.min分别为节点电压的上边界值与下边界值;Ql.max、Ql.min分别为发电机无功输出的上边界值与下边界值。
1.2 功率平衡等式约束条件
功率平等的等式约束条件为
式中:Pi、Qi分别为发电机在i节点处的有功输出与无功输出;N为节点集合;Gij、Bij分别为电力系统各节点导纳矩阵中的实部和虚部。
1.3 无功优化的不等式约束条件
在无功优化建模中,考虑到控制参数限制条件和状态参数限制条件,控制参数选择各发电机端电压的幅值UG、可调档变压器分接头位置值KT、无功补偿装置投切组数UC。
约束条件为
式中,UGmax(UGmin)、KTmax(KTmin)、UCmax(UCmin)分别为UG、KT、UC的上(下)极限值。
选择电力系统中节点电压的模值UL、电力系统中发电机无功输出值QG为状态参数。
约束条件为
式中:ULmax(ULmin)、QGmax(QGmin)分别为UL、QG的上(下)极限值。
2 改进的快速群搜索优化算法
2.1 改进的群搜索算法
设在n维搜索空间中,第i个个体在第k次迭代后,其位置可表示为在搜索空间中的搜索角为,搜索方向为其中
在传统的种群搜索算法中,觅食行为模式包括发现者、搜索者、游荡者,其中发现者按照以下步骤遍历性寻找食物[12]。
(1)设发现者初始搜索角为 0°,按式(8)向正前、左侧方、右侧方各搜索一个点。
式中,Ui、Li分别为设计变量的上、下界。
(2)计算得出各个位置的适应度。若新探索出的位置与原个体位置相比有更优的个体位置适应度,种群中的发现者会以最快的速度移动至此位置;否则,维持原个体位置不变,按式(10)调整搜索方向,准备进行下一次迭代搜索。
式中,αmax为最大搜索转角。
(3)假设种群中的发现者个体经过a次迭代,在种群搜索空间内依然没有探索到更优的位置,则依据式(11)将此个体的空间搜索角重置为 0°。
式中,a为设定的常数。
80%的剩余个体作为搜索者,追随发现者的位置可表示为
式中,r3为[0,1]区间内具有均匀分布特性的任意数。20%的剩余个体视为种群搜索中的游荡者,分散在种群内,此参数依据表达式(10)的逻辑重新判定搜索角度,按式(13)确定搜索距离,再按式(14)移动到更优位置上。
2.2 优化快速群搜索算法
优化后的快速群搜索算法(FGSO)不改变原传统种群搜索算法GSO的群体内各个个体贡献行为模式分类,仍采取发现-搜索的模式进行空间范围内随机搜索。
针对原始算法存在的问题,文中所提改进算法在算法运算的三个步骤进行了相应的优化处理.
(1)若算法停止运算不再前进时,可依据算法的进程情况合理选择增加游荡者存在的数量。
(2)改进个体位置极坐标向笛卡尔坐标的转换方法,由于多个接近于0的数乘积也趋于0,所以将的前n-t0-1个数值,直接置0,其中t0用于控制置0个数,这样缩短了计算用时,减少运算步骤,而且算法的遍历搜索能力不受影响,这里t0取值为8;将目标循环平移因子引入到算法搜索当中,即Circshift(X,y),其含义为将向量X进行循环平移,平移y个元素,如
则改进后的坐标转换公式为
式(8)改进后为
式(14)改进后为
(3)引入遗传算法,将遗传算法与群搜索算法进行耦合,通过搜索到的个体最优值和种群空间最优值的融合产生新的游荡者。
2.3 快速搜索实现过程
初种群每个个体的初始位置设为任意值,在n维空间中搜索,空间中存在的第i个个体在进行了k次迭代后的位置设为。
在进行第k次参数迭代时,计算出每一个种群个体的位置适应值,将位置适应值更优者作为发现者,其位置表示为。余下的种群个体中任选80%的个体作为搜索者,引入循环平移因子,搜索者以任意步长向确定发现者靠近,可表示为
式中,r为n维向量,其元素为[0,1]中具有均匀分布特性的任意数;ω1、ω2是搜索过程中负责觅食信息传递的算子;为第i个个体在第k次迭代时的最好历史位置。
搜索者靠近发现者后接收发现者的位置信息和自身信息。其余个体的20%作为游荡者,寻找下一个发现者,其公式为
式(19)~式(21)中:4ω为维度内个体发生变异的概率;rand(n,1)为n维均匀分布任意数的函数,所生成随机数表示出现正向分量的概率;“<”表示比较“=”号两端所表示的分量数值,据此可得到所需的布尔值。I为全1向量。
式(21)表示种群中的游荡者以不变的维度变异概率与发现者进行信息置换,使游荡者获取足够的位置信息,以便于搜寻下一个位置适应值更好的发现者,大大提升了算法的收敛速度。
在约束边界处理上,借鉴改进粒子群算法中[13],对于飞出自变量边界的个体,重新生成位置值,步骤如下。
步骤1找到飞离自变量边界的个体。
步骤2分析个体位置Xi,辨识分量是否违反了相应自变量的边界条件,即
步骤3在种群个体历史位置最优矩阵Pbest中的相应个体位置任选一个值来代替该维分量,即
3 基于FGSO算法的配网无功优化
将FGSO算法应用于电力系统无功优化过程,步骤如下。
步骤1系统初始化。输入潮流数据、控制变量的约束范围等。
步骤2算法初始化。利用随机值初始化种群内个体位置和搜索速度,设定快速群搜索算法的种群规模及最大迭代次数。
步骤3潮流计算。对当前种群中所有个体进行潮流计算,将其中有功网损最小的个体作为发现者,剩余种群的80%作为搜索者,20%为游荡者。
步骤4对发现者进行局部寻优。
步骤5利用式(18)更新发现者位置,根据式(21)更新游荡者位置。
步骤6计算更新的种群个体适应度,即求电力系统的有功损耗。将电力系统有功损耗最小者作为发现者,对终止条件进行判断,若满足,执行步骤7;否则,返回步骤3。
步骤7无功优化算法进程结束,输出系统有功网损最小值。
FGSO算法流程见图1。
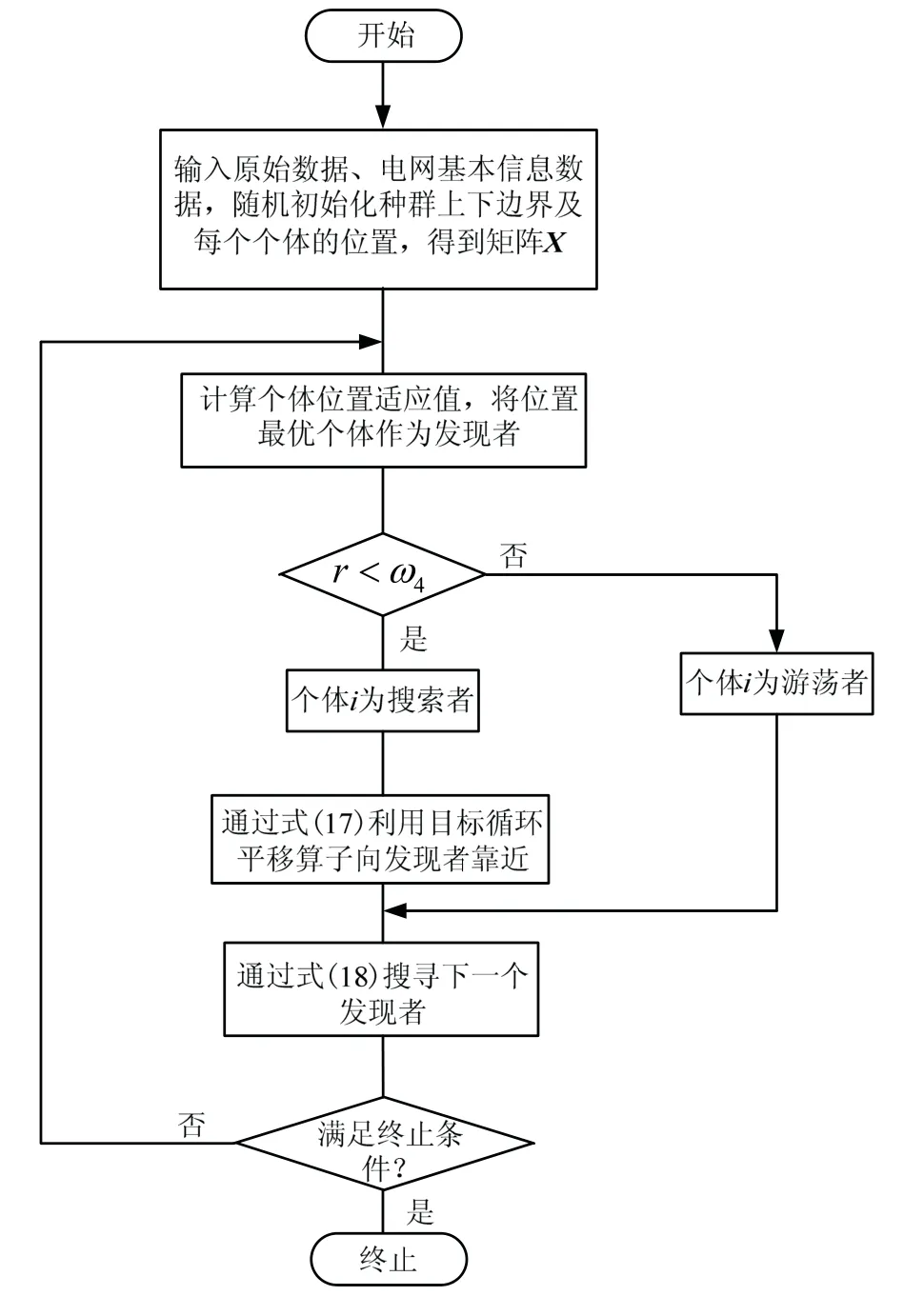
图1 FGSO算法流程Fig.1 flow of FGSO algorithm
4 算例分析
采用标准IEEE30节点系统来验证FGSO算法的可行性和优越性,将其无功优化结果分别与HPSO(改进粒子群算法)及GSO算法的优化结果进行比较。开展3种算法的仿真分析。其中,HPSO算法参数取值如下:种群规模为50,惯性因子遵从0.9→0.4的线性衰减规律,加速因子c1和c2均取8。GSO算法参数取值如下:初始搜索角φ0取45°,常数a取的整数,最大搜索角度θmax取π/a2,最大搜索转角αmax取π/2a2,迭代次数取200。FGSO算法参数取值如下:当目标向前进行时,惯性因子ω1、ω2、ω3、ω4分别取4、4、0.2、0.65;当目标停止向前时,惯性因子ω1、ω2、ω3、ω4分别取0.8、1.5、0.35、0.85;迭代次数取200。
仿真算例采用标准IEEE30节点电力系统,其发电机的无功输出上下界限见表1。
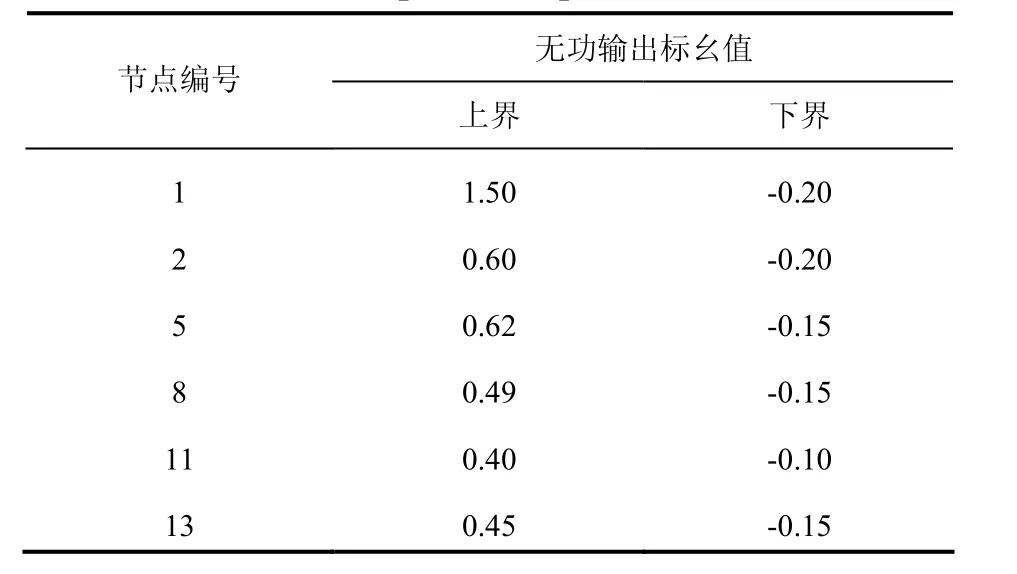
表1 发电机无功出力上、下限标幺值Tab.1 upper and lower limits of generator reactive power output
系统中,各发电机节点的电压标幺值上、下限分别为1.1和0.9;各用户负荷节点的电压标幺值上、下限分别为0.95和1.05;配电变压器的变比调整上、下限分别为0.9和1.1;搜索调整步长设为0.02;无功补偿装置的电容器最大投切组数设为4,节点10和节点24的单组补偿容量依照标准值设定;基准容量S为100 MVA,设可调变压器的初始变比为1,发电机初始电压标幺值为1,无功补偿点初始标幺值为0,则系统初始网络损耗Ploss为0.0855。
为验证各算法的稳定性,将HPSO算法、GSO算法、FGSO算法分别计算50次,得出每种算法有功网损的最大值、最小值和平均值,见表2。
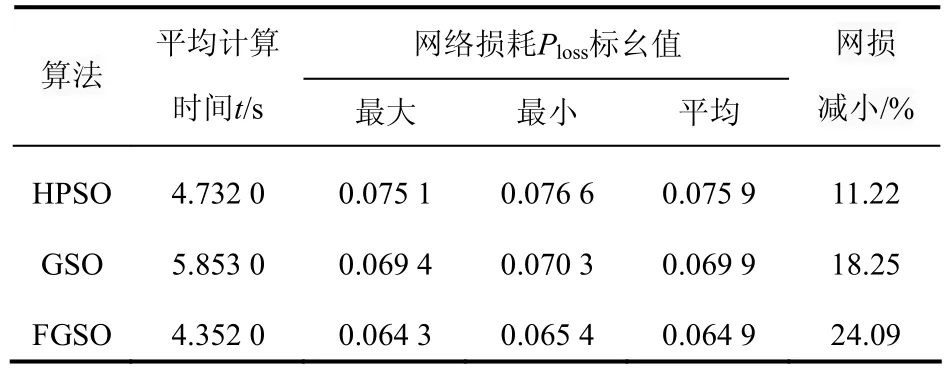
表2 3种算法的网络损耗优化结果Tab.2 optimization results of three algorithms
从表2可以看出,与其他2种算法相比,FGSO算法计算时间最短,其有功网损减小最大,为24.09%,证明FGSO算法有较高的计算效率和收敛精度,有较强的全局搜索性能,能更精准、更快速地求得优化问题的最优解。
FGSO算法进行优化后的控制参数见表3。
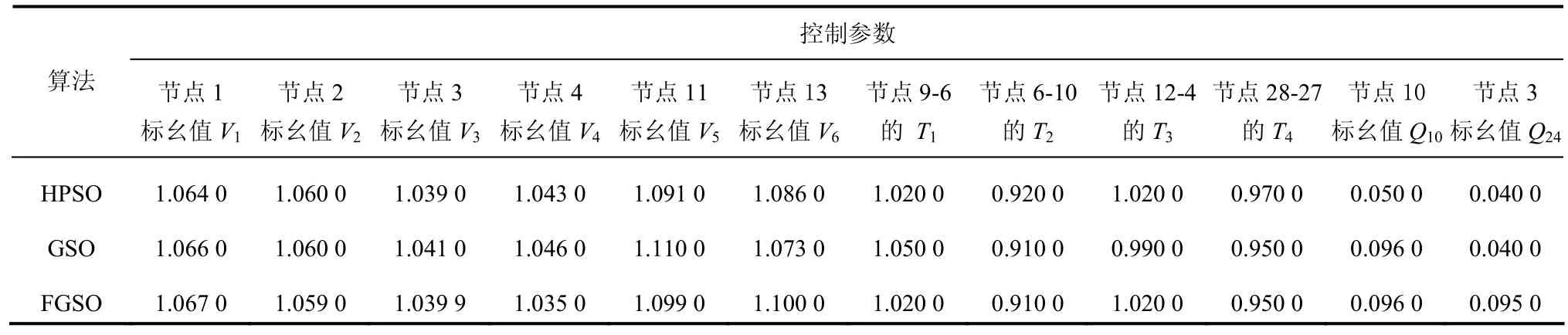
表3 IEEE30节点经优化后的控制参数Tab. 3 optimized control parameters of IEEE-30 node
在200次的迭代过程中,不同算法的目标函数值收敛情况见图2,电网无功优化后的系统节点电压见图3。
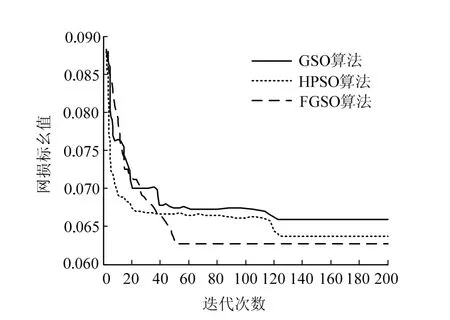
图2 3种算法的目标函数值Fig.2 objective function values of the three algorithms

图3 3种算法节点电压Fig.3 voltage of three algorithms
从图2可见,FGSO算法的收敛速度明显高于其他两种算法,迭代50次左右,该算法就已经收敛。从图3可见,与其他两种算法相比,FGSO算法优化后的系统各节点电压没有电压越限,FGSO的对电压幅值提升较为显著。
5 结论
在传统群搜索算法的基础上提出一种快速群搜索算法(FGSO算法)。当FGSO算法不前进时加大游荡者数量,将种群中个体位置的极坐标向笛卡尔坐标转换;引入目标循环平移因子,加快算法的运算速度;融合遗传算法,将个体最优值和种群最优值相结合,杂交产生新的游荡者,提高种群多样性。利用国际标准的IEEE-30电力节点系统对FGSO算法进行性能验证,结果表明:与HPSO算法、GSO算法相比,FGSO算法的优化能力和鲁棒性更强,在一定程度上解决了现有算法求解过程复杂、收敛速度较慢、计算效率低等问题。

