电力巡检机器人机械臂的运动规划虚拟系统

余 凌，刘 飘，罗金满，王湘女

（广东电网有限责任公司东莞供电局，广东 东莞 523008）

0 引言

带作业机械臂的电力机器人可以减轻人工劳动强度，解决现有巡检设备只有检测功能没有操作功能的问题，实现电力机器人代替人工来安全地完成作业，某种程度上解决了人工作业效率低和高风险等问题［1-5］。电力机器人作业时是依靠机械臂来完成任务的，机械臂的末端装有末端执行器来操作不同的任务。为了高效安全地实行机械臂自主执行任务，如带电导线捡拾、螺栓紧固等，需要对机械臂的关节空间进行实时的运动轨迹规划。如日本公司所研发的带电作业机器人Robot-PhaseⅢ可实现半自动化作业，能自主识别目标位置并进行运动规划。

目前大部分对机械臂的运动规划研究集中在运动规划方法上。栾庆磊提出一种改进型渐进最优快速随机扩展树（RRT*）算法用于路径规划，解决机械臂在运动路径规划上搜索随机性强、成功率低的问题［6］；陶志远针对断路器带电检修机器人的机械臂作了路径规划关键技术研究［7］；邾根豪提出了一种针对带电作业机器人基于时间最优的轨迹规划算法和控制策略研究［8］。韩波等对机械臂的运动学算法进行了建模和设计［9-14］。以上研究在不同方向上对机械臂的运动规划方法优化等做出了贡献，但较少涉及其规划算法后对机械臂的三维动态仿真内容。在实际的机械臂作业过程中，单凭操作人员的想像很难预测机械臂的运动规划后的轨迹，一旦规划出现问题，机械臂的运动状况将无法预测。基于此，以用户设计为中心，本文设计一个基于四自由度电力巡检机器人机械臂的运动仿真系统来模拟机械臂的运动过程，实现机械臂的常规运动仿真和轨迹规划仿真。

1 作业机械臂的建模

电力巡检机器人的作业环境通常是非规则化的，当需要机械臂进行操作时，如需要快速将带电导线与被保护物分离时，操作导线的周边物品会不可避免地成为障碍物，给作业带来不便。为此，面向普适计算方法，对操作机械臂先进行运动建模研究。机械臂的运动学分析是运动规划的前提基础，可分为机械臂的正运动分析与逆运动分析两个方面［15-16］。本文采用四自由度的操作机械臂作为研究对象，只对主要运动部件进行建模型，分别为基座、旋转平台、大臂和小臂以及末端机构，四个自由度均为旋转型关节，如图1所示。

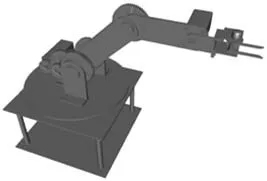
图1 四自由度操作机械臂Fig.1 Manipulator arm with four degrees of freedom

1.1 机械臂正运动分析

机械臂正运动分析是指根据已知机械臂连杆参数与机械臂的运动坐标系，建立一数学模型。该模型是以机械臂各关节量(θ)作为输入变量，以机械臂末端执行器坐标值为输出变量。然后利用该模型可根据已知的机械臂各关节量得出机械臂末端执行器在空间坐标系的坐标值。首先根据机械臂关节坐标系和广义连杆的4 个Denavit-Hartenberg（D-H）特征参数(d，k，a，θ)定义，绘制出机械臂处于初始状态时的运动学坐标系，具体如图2 所示。(d，k，a，θ)4 个参数含义分别是d为连杆偏距，k为连杆长度，a为连杆转角，θ为关节角；然后根据机器人矩阵学知识求出各机械臂连杆的相对变换矩阵T（其中i表示机械臂连杆的编号，i-1 即表示上一连杆的编号，i≥1）；最后将各机械臂连杆的变换矩阵相乘得出末端执行器相对于基座标的变换矩阵05T。05T变换矩阵能够根据机械臂各连杆关节变量(θ)的具体值，通过计算后得出末端执行器在基坐标系的位置和姿态。05T的得出如公式（1）所示。

图2 机械臂运动学坐标系Fig.2 Kinematic coordinate system of manipulator

式（1）中，用n，o，a，p分别表示矩阵中的元素。nx表示矩阵中第一行第一列的元素；ox表示矩阵第一行第二列的元素；ax表示矩阵第一行第三列的元素；px表示第一行第四列的元素；ny表示矩阵中第二行第一列的元素，其余类推；nz表示第三行第一列的元素，其余类推。

1.2 机械臂逆运动分析

机械臂逆运动分析是正运动分析的逆过程，是指在已知各连杆几何参数的情况下，给定末端执行器在其坐标系中的期望坐标值，求出要使末端执行器运动到期望位置时每个关节所应该运动的数值量。利用变换方程式（1）求出各连杆关节变量(θ)。机械臂逆运动分析的最终目标是求出各关节变量(θ)的解析表达式，常用的方法有代数解法与几何解法。根据实际的操作机械臂结构与对计算量的考虑，本文采用几何解法与代数法相结合解法。先用代数解法求出底座旋转关节的表达式，然后绘制出机械臂各连杆（大臂旋转a1，中臂旋转a2，小臂旋转a3）的姿态位置图，如图3 为机械臂运动到某一时刻时的姿态位置简图，最终得出其他各变量的解析表达式。

图3 机械臂连杆位置简图Fig.3 Mechanical arm link position diagram

2 改进A*算法的机械臂避障路径规划

由于C 空间具有直观、易于实现以及在运用合适搜索方法的情况下可找到最优运动路径，且机械臂常用的路径规划方法为C 空间法，因此本文采用基于C空间的路径规划方法［17］。根据C空间的特点建立机械臂的C 空间并进行了C 空间障碍的栅格化表示后，采用A∗搜索算法，搜索一条以起始位置点为起点，目标位置点为终点的无碰撞路径［18-28］。

A∗搜索算法在搜索过程利用一个估价函数作为搜索指标，该函数表示为f∗(x) =g∗(x) +h∗(x)，其中f∗(x)表示从起始节点到节点x的一条最佳路径的实际代价加上从节点x到目标节点的一条最佳路径的代价之和；g∗(x)表示从起始节点到节点x之间最小代价路径的实际代价；h∗(x)表示从x节点到目标节点的最小代价路径上的代价。然而实际上f∗(x)是无法预先知道的，解决办法是用函数f(x) =g(x) +h(x)来近似代替以上估计函数，其中必须满足条件g∗(x) ≤g(x)，h∗(x) ≥h(x)。对于搜索算法在二维C-空间栅格平面上进行搜索时，每次搜索的方向有8 个，如图4所示。

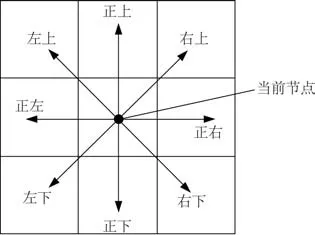
图4 二维平面的8个搜索方向Fig.4 Eight search directions in a two-dimensional plane

由于机械臂的运动空间属于三维空间，使用搜索算法搜索时每次搜索的方向就变为26个，每次扩展的节点也变为26个，此时搜索算法每次扩展的节点一下子变成了二维平面的3 倍之多，这样不仅会增加节点存储空间的使用，而且会严重影响搜索的速度。为了让A∗搜索算法能够适用于三维栅格C-空间，对A∗搜索算法的实现进行改进，具体为：对三维C空间上的任意一点，可以看成是三维空间的xy平面、yz平面以及xz平面这3个平面上的一点，因此，对于起始点与目标点不在同一个平面的情况，可先分别对起始点与目标点设定不同的从属平面，如起始点从属于R 平面而目标点从属于r0平面，如图5所示。

图5 改进的A∗搜索算法原理图Fig.5 Improved A∗ search algorithm schematic

然后在这两个从属平面的相交处找出一个中间点，此时三维路径搜索问题可转换成两个二维平面的路径搜索问题的合成，这样便可利用A∗搜索算法分别在两个从属平面搜索出最优路径，然后再将这两条路径组合成最终的搜索路径。具体的操作步骤如图6所示。改进后的A∗搜索算法分别从两个平面上搜索出两条路径，然后组合起来得出最终三维C 空间的运动路径，其相对于直接使用A∗搜索算法在三维空间中搜索，不仅节省了搜索过程节点的存储空间，而且还加快了搜索的速度。

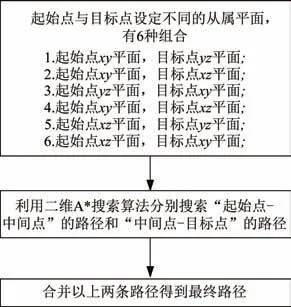
图6 改进的A∗搜索算法流程图Fig.6 Improved A∗ search algorithm flow chart

3 操作机械臂的运动规划仿真系统

3.1 机械臂运动仿真系统设计

本次仿真采用Visual Studio 为编程工具，使用Eon Studio 作为仿真程序接口，实现了单一障碍物的操作机械臂避障运动仿真。为了便于研究，用经过简化处理的四自由度运动模型实体代表操作机械臂，以长圆柱体模型作为障碍物以及用小圆球代表运动目标点。为了配合路径规划，将机械臂简化为二自由度，只实现两连杆的运动，仿真的目标是让连杆2 的端点运动到指定的目标点。首先，利用Visual Studio 编写主体程序框架，在程序里实现运动反解程序，路径搜索程序以及轨迹规划程序；其次，把操作机械臂运动模型导入Eon Studio 中进行虚拟仿真程序的设计；最后，Eon 虚拟仿真程序以Eon Studio控件形式嵌入到Visual Studio主程序框架中，利用Eon Studio 控件提供的接口函数，Visual Studio 可对仿真程序进行控制以及对仿真程序事件进行响应，仿真流程如图7所示。

图7 操作机械臂运动仿真流程图Fig.7 Movement simulation flow chart of manipulator

3.2 机械臂运动仿真系统测试验证

机械臂运动仿真系统的目的是在设定的具体条件下验证规划后的运动轨迹光滑平稳性。所设置的机械臂包括连杆1和连杆2，并设置抓取的对象为目标小球和设定障碍物。具体步骤为：

1）设定仿真条件，设连杆1与连杆2长度同为500，两连杆关节初始值同为00。假设目标点在基座标系的位置为（600，0，300），障碍物的位置为（600，0，200）。

2）运行运动学反解程序，路径搜索程序以及轨迹规划程序，得出两关节运动路径点和平滑后的运动曲线，如图8和图9所示。

图8 连杆1关节位移时间运动曲线Fig.8 Joint displacement time motion curve of Connecting Rod 1

图9 连杆2关节位移时间运动曲线图Fig.9 Joint displacement time motion curve of Connecting Rod 2

3）在Visual Studio主程序框架中根据设定的路径曲线进行运动仿真。为了让机械臂的运动更逼近两关节的运动曲线，在主框架程序中设定仿真运动每隔0.1 s 更新一次关节的位置，如图10 所示。图10（a）表示机械臂的初始状态，此时两连杆关节的值为00；图10（b）表示机械臂运动仿真过程的某一状态，由于运动位置点经过路径规划以及轨迹规划，因此连杆的运动不但可避开障碍物，而且还可实现平稳过渡；图10（c）表示机械臂运动到目标位置点。算例验证了所搭建的电力机器人机械臂运动的有效性。

图10 机械臂避障运动仿真Fig.10 Simulation of obstacle avoidance motion of mechanical arm

4 结语

应用虚拟现实技术、普适任务计算的思想，把机器人机械臂的任务分解，从操作目标、运动规划和计划计算出发，构建了机器人运动规划数学模型，在虚拟环境下进行了三维运动仿真。利用Visual Studio 编程工具以及Eon Studio 仿真软件对以上研究结果进行仿真实验，为实际操作机械臂运动控制提供参考依据，也为虚拟人体运动和机器人运动提供了一种计算方法。