面向电厂设备异常检测的自组织映射深度自编码高斯混合模型研究

耿 波，李青松，潘曙辉，董晓旭

（1.核动力运行研究所，湖北 武汉 430223；2.华中科技大学计算机科学与技术学院，湖北 武汉 430074；3.华北理工大学冶金与能源学院，河北 唐山 063210）

0 引言

随着现代技术的飞速发展，工业生产设备也正在走向高度机械化、自动化和智能化［1］。工业设备的高效生产和稳定运行维持着社会的稳定发展。为降低生产设备的维护成本、提高生产效率，有关生产设备异常检测的研究显得尤为重要。

生产设备是指企业或工厂中产生能源、物质产品等的机械、仪器或装置。例如，电能如今已成为人们工作、生活、娱乐的不可或缺的能源，然而当电厂的生产设备一旦发生异常或故障，极易带来社会的损失和不便［2］。当机组设备发生异常时，若不及时处理，容易损坏，进而产生紧急成本和较长的维护时间，情况严重时伤亡事故也有可能发生［3］。直接来说，因生产设备故障造成工厂停机，会导致每小时产生上万甚至十万美元损失，甚至一天可能产生高达上百万美元经济损失［4］。因此，尽可能在早期检测出电厂生产设备的异常情况，给予工作人员排查和诊断的时间更有利于减少不必要的时间和经济损失。

生产设备的异常检测是通过一系列传感器件或智能感知设备，采集设备在运行状态下的各项参数，利用基于数据驱动的手段和数据分析方法，判断设备当前是否处于异常状态。近数十年来，出现了很多的异常检测技术。其中，针对研究领域的不同可分为专业领域和普通情景两类；基于在训练数据时是否带有标签信息，又分为无监督、半监督和有监督3类。现有的异常检测技术庞杂，而现实应用中无监督情况较多［5］，故无监督的异常检测技术的研究更具现实意义。异常检测技术的广泛应用推进了它的方法优化［6-8］。

目前的无监督传统异常检测技术分为以下四类：1）基 于 相 似 性 度 量，如K 近 邻 算 法（K-Nearest Neighbor，KNN）［9］、局部异常因子算法（Local Outlier Factor，LOF）［10］等；2）基于聚类，如基于K-means 算法［11］，基于DBSCAN算法［12］，基于高斯混合模型［13］等；3）基于降维，主要是使用合适的方法最大程度地保留原始数据的关键信息。此类方法包括主成分分析（Principal Component Analysis，PCA）［14］以及基于它的改进算法。4）基于分类，即构造出异常检测的分类器，此类方法通常包括了一类支持向量机（One-Class Support Victor Machine，OCSVM）［15］，孤 立 森 林（Isolation Forest，iForest）［16］等。目前，深度学习在学习高维数据、时序数据和图片视频等复杂数据的特征表达上展现出了强大的能力。深度异常检测（Deep Anomaly Detection，DAD）是通过神经网络来学习特征表示以便进行异常检测的方法［17］，近几年，已出现的深度异常检测技术、方法、模型有很多，如RandNet［18］、AE-1SVM［19］，在处理各种实际使用中存在挑战的异常检测问题方面，表现出比传统异常检测明显更好的检测效果。

高斯混合模型（GMM）是工业界内使用最广泛的异常检测技术之一。深度自编码高斯混合模型（DAGMM）［20］是基于高斯混合模型改造的深度异常检测技术，由一个压缩网络和一个估计网络构成，并且可以进行端到端的训练，克服了之前部分模型无法在低维空间中保存信息的问题。但DAGMM 仍面临着GMM 的低维需求和保留高维结构需求之间选择的两难境地。

本文针对深度自编码高斯混合模型存在的异常检测问题进行改进。首先针对DAGMM，利用UMAP 算法原理将其改造成一个降维网络，通过在原有损失函数上增加交叉熵的方式将高维数据分布信息补充进去，得到基于均匀流形近似与投影增强的深度自编码高斯混合模型UMAP-DAGMM，再结合自组织映射网络依靠竞争学习的特性，最终得到自组织映射辅助的增强型深度自编码高斯混合模型SOM-UMAPDAGMM。

1 自组织映射辅助的增强型深度自编码高斯混合模型

深度自编码高斯混合模型由于其压缩网络采用的深度自编码器仅仅是一个基础的结构，主要目的是用于压缩满足后续密度估计的低维需求，所以几乎不能保留原始数据分布和空间拓扑这些高维信息。均匀流形近似与投影（Uniform Manifold Approximation and Projection，UMAP）［21］，是一种新的降维可视化技术，由于其是非线性的，可以更好地保留高维空间的全局和局部信息。自组织映射（Self Organizing Map，SOM）［22］方法可以保留输入空间的拓扑结构。因此本文提出自组织映射辅助的增强型深度自编码高斯混合模型（Self-Organizing Map assisted Deep Autoencoding Gaussian Mixture Mode with Uniform Manifold Approximation and Projection，SOMUMAP-DAGMM），通过将UMAP算法改为降维网络融合进DAGMM中，并借助预训练的SOM，以补充高维数据分布信息以及空间拓扑结构信息。

1.1 UMAP-DAGMM

由于UMAP算法是以交叉熵为损失函数，利用梯度下降进行迭代更新，尝试通过将UMAP算法修改为降维网络，通过新增的交叉熵损失函数来增强低维表示中的高维数据结构信息，提出基于均匀流形近似与投影改进的模型（Deep Autoencoding Gaussian Mixture Model with Uniform Manifold Approximation and Projection，UMAPDAGMM）。

1.1.1 UMAP-DAGMM网络结构

UMAP-DAGMM 的网络结构如图1 所示，压缩网络保持与原来DAGMM 中不变，UMAP 网络是由全连接层组成，输出特征向量、重构误差和深度编码器压缩特征共同组成估计网络的输入特征向量。估计网络结构也保持原网络结构不变。其中UMAP网络使用欧式距离作为度量计算高维分布，利用神经网络的随机正态初始化来代替原本UMAP 低维坐标初始化方法，并利用一些神经网络中调参技巧来解决欠拟合和过拟合问题。

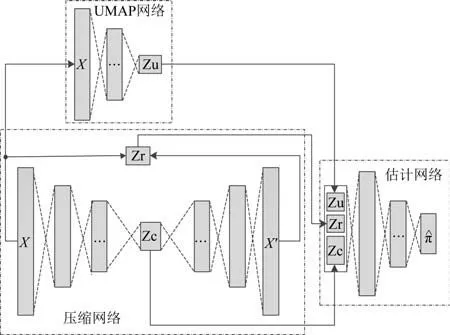
图1 UMAP-DAGMM结构示意图Fig.1 Schematic diagram of UMAP-DAGMM structure

UMAP-DAGMM 的工作原理如下：1）压缩网络使用深度自编码网络，对训练样本降维；2）UMAP改编而成的网络对训练样本降维补充高维信息；3）估计网络在GMM框架下预测样本的能量。进行异常检测时，样本能量超过设定阈值则为异常，运用异常检测评价指标对模型性能进行分析。

1.1.2 UMAP-DAGMM损失函数UMAP-DAGMM的完整损失函数如公式（1）所示。

式（1）中，等式左侧中，θu、θc、θd、θm分别为UMAP 网络、编码网络、解码网络、估计网络的参数。

式（1）等式右侧中，N为样本数量，λ0、λ1、λ2为3个超参，分别设为1、0.1和0.005。

UMAP网络使用交叉熵。由于梯度下降算法与梯度有关，为了加快运算速度，忽略包含原始分布P的常数项，对交叉熵公式优化如式（2）所示。

式（2）中，P为原始数据高维空间数据分布；Q为UMAP降维后的数据分布。由此可得，简化后交叉熵如式（3）所示。

压缩网络的重构误差同自编码器，计算公式如式（4）所示。

估计网络的样本能量（energy）损失利用GMM 的概率密度函数，尽可能使样本的概率密度更大，密度估计的输入z由压缩网络的瓶颈层与重构误差构成，估计网络的样本能量损失函数如式（5）所示。

为防止估计网络计算时协方差矩阵的对角线变为0 最终导致矩阵不可逆，加入以下正则项如式（6）所示。

式（6）中，d表示低维压缩特征的维数，Σ̂kj表示第k个高斯分量的协方差矩阵中第j个对角元素。

1.2 SOM-UMAP-DAGMM

为了进一步优化UMAP-DAGMM，不同于UMAPDAGMM 仅利用一种降维方法，SOM-UMAP-DAGMM同时利用UMAP 和SOM 来补充原始数据的不同高维信息，以此改善在实际生产设备上DAGMM 的性能不足问题。

自组织映射（Self Organizing Map，SOM）是一种基于竞争性学习的无监督降维可视化算法，它使用人工映射神经网络将训练样本离散化到低维（通常是二维）空间，因此该技术广泛应用于数据分析或数据可视化等［23］。SOM 与使用反向传播训练的一般神经网络不同，它采用竞争学习的策略，依靠神经元之间互相竞争逐步优化网络。SOM强调生成一个低维、离散的映射空间，并具有输入空间的拓扑结构，故而训练过程中采用近邻关系函数来维持输入空间的拓扑结构。因此，SOM 可作为一个独立的分支，作为辅助工具，获取低维平面上反映原始数据的空间拓扑关系的数据。

1.2.1 SOM-UMAP-DAGMM网络结构

如图2所示，展示了SOM-UMAP-DAGMM 的总体层次结构，该图在UMAP-DAGMM 的基础上增加了SOM预训练辅助。如前所述，通过SOM强大的保持空间拓扑能力进一步加强模型性能。

图2 SOM-UMAP-DAGMM网络结构示意图Fig.2 Schematic diagram of SOM-UMAP-DAGMM network structure

具体来说，采用分阶段训练方法［24-32］解决梯度下降与无梯度竞争学习之间的冲突。给定原始特征x作为输入，第一阶段首先训练SOM以生成低维表示zs；第二阶段进行UMAP-DAGMM训练，UMAP用x生成的低维空间为zu，深度自编码器用x生成的低维码zc，并用x和x'计算重构误差zr。低维表示定义如式（7）所示。

另外，SOM 及其对应的编码zs在第二阶段训练时保持不变；损失函数与UMAP-DAGMM相同；决策函数使用样本能量，如式（8）所示。

1.2.2 SOM-UMAP-DAGMM训练策略

如图3 所示，SOM-UMAP-DAGMM 的训练过程包括：1）依赖于无梯度的竞争学习规则的SOM 子过程；2）依赖于梯度的UMAP-DAGMM子过程。

图3 SOM-UMAP-DAGMM训练示意图Fig.3 Schematic diagram of SOM-UMAP-DAGMM training

具体来说，将数据集分成训练集和测试集。鉴于此模型为无监督的，训练集无需标签，而测试集则保留标签用于性能评价。训练数据先对依赖竞争学习的特殊神经网络SOM 进行训练，训练结束后将训练好的SOM 保存下来。经过训练的SOM 和由此获得的zs在后续UMAP-DAGMM训练期间不参与更新。之后利用神经网络的反向传播完成梯度下降的迭代更新。

SOM-UMAP-DAGMM 继 承了SOM-DAGMM 核心思路和训练流程，通过预训练SOM，更好地完整保留高维空间拓扑信息，从原来的网络入侵数据集来看，这种做法确实能有效提升模型的性能和稳定性。

为了更加清晰地理解整个算法流程，详细给出SOM-UMAP-DAGMM的伪代码如图4所示。

图4 算法的过程描述Fig.4 Process description of Algorithml

2 实验结果和分析

2.1 实验数据集

本文中实验所采用的数据集分为公开数据集和国内某电厂生产设备数据集两部分。公开数据集是采用异常检测常用的数据集Arrhythmia 和Thyroid，如表1所示。Arrhythmia 是心律失常数据集，用于区分是否存在心律失常并分类；Thyroid 是甲状腺数据集，根据甲状腺的存在和缺失分布定义为正常和异常。

表1 公开数据集Table 1 Public dataset

生产设备数据集来自于国内某火电厂，为生产设备运行时传感器每分钟回传的参数，数据共3组，分别来自3 个不同的生产设备，高压加热器（JRQ）、一次风机（FAN）、凝泵电机（NJSB），如表2所示。异常数据经过人工标记（标记可能存在少量误差），特征维数中包含标签。

表2 国内某电厂生产设备数据集Table 2 Dataset of production equipment of a domestic power plant

2.2 评价指标

异常检测的数据集一般都是不平衡数据集，因此不能简单地使用二分类的准确率去评价算法的好坏，对于更加注重异常的这些模型而言评价指标更为复杂。

对于异常检测模型，预测为真真实为真为真阳数（TP），预测为真真实为假为假阳数（FP），预测为假真实为真为假阴数（FN），预测为假真实为假为真阴数（TN）。

则准确率如式（9）所示：

精确率如式（10）所示

召回率如式（11）所示

计算F1Score如式（12）所示

F1Score是精度与召回率权衡的指标，能更好地直接评价异常检测模型的好坏。对于生产设备而言，精度过低会导致误报加重维修人员排查工作量，召回率过低会产生漏报导致设备无法尽早维护产生损失。故而在召回率不差的情况下，精度较高才是符合实际情况的。

2.3 实验参数设置

在公开数据集Arrhythmia 中，UMAP 网络、压缩网络、估计网络参数设置如下：

FC（274，64，tanh）→Dropout（0.5）→FC（64，32，tanh）→Dropout（0.5）→FC（32，2，tanh）；

FC（274，10，tanh）→ FC（10，2，none）→FC（2，10，tanh）→FC（10，274，none）；

FC（6，10，tanh）→Dropout（0.5）→FC（10，2，softmax）。

在公开数据集Thyroid 中，UMAP 网络、压缩网络、估计网络参数设置如下：

FC（6，10，tanh）→Dropout（0.5）→FC（10，5，tanh）→Dropout（0.5）→FC（5，2，tanh）；

FC（6，12，tanh）→FC（12，4，tanh）→FC（4，1，none）→FC（1，4，tanh）→FC（4，12，tanh）→FC（12，6，none）；

FC（5，10，tanh）→Dropout（0.5）→FC（10，2，softmax）。

其中，FC 指全连接层，数字表示全连接的节点数量；Dropout 表示按照概率将神经元在训练时丢失；tanh、softmax表示对应的激活函数；none表示该层无激活函数。

对于生成设备的数据集，实际参数可能包括温度、压强、气流等特征参数，这些参数的量纲存在很大的差别，因此在传入网络之前先使用Z-Score 方法进行预处理。

对于深度自编码高斯混合模型，针对数据集的维度和大小，设置参数如表3所示。

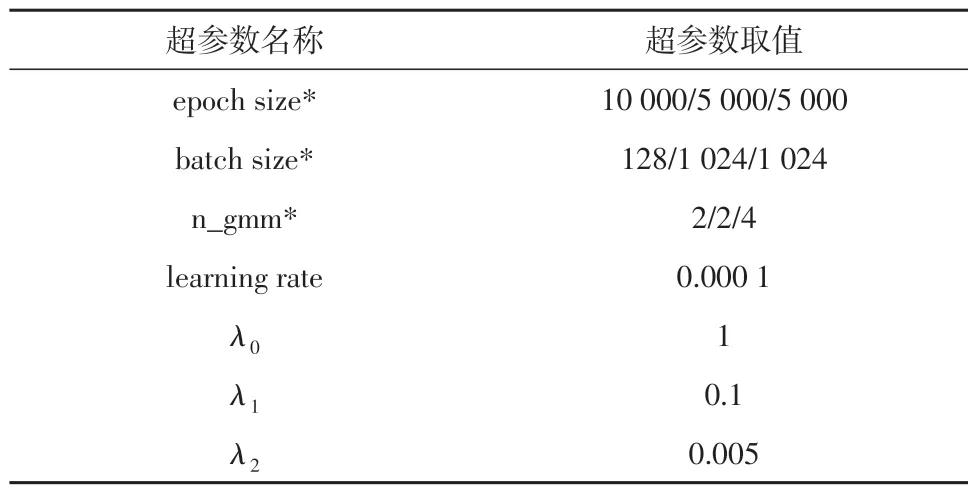
表3 DAGMM默认超参数设置Table 3 Default hyperparameter setting in the DAGMM

UMAP 算法有两个重要的超参数：min_dist 和n_neighbor，用于调节最后投影中全局与局部结构间的平衡。其中，min_dist 即在低维空间中点之间的最小距离，用于控制低维点聚集的密集程度，低值紧密，高值松散；n_neighbor 即初始高维空间近似最近邻居点的数量，用于控制局部细节与全局结构平衡。不同的参数取值对UMAP-DAGMM 模型性能有一定的影响，在实验中对于两个公开数据集以及四个生产数据集，UMAP的超参数取值如表4所示。

表4 UMAP-DAGMM超参数设置Table 4 Hyparameter setting in the UMAP-DAGMM

SOM 可以通过调整初始学习率（η_SOM）和领域函数（f_neighborhood）来提高性能。SOM-UMAPDAGMM中SOM的参数设置如表5所示。

表5 SOM-UMAP-DAGMM超参数设置Table 5 Hyparameter setting in SOM-UMAP-DAGMM

2.4 实验结果及分析

按照以上2.3 节的超参数设置，在公开数据集Arrhythmia 上 ，DAGMM、UMAP-DAGMM、SOMUMAP-DAGMM模型的实验结果如表6所示。

表6 Arrhythmia数据集实验结果Table 6 Dataset experimental results of Arrhythmia

在公开数据集Thyroid 上、DAGMM、UMAPDAGMM，SOM-UMAP-DAGMM 模型的实验结果如表7所示。

表7 Thyroid数据集实验结果Table 7 Dataset experimental results of Thyroid

在生产数据集JRQ 上，DAGMM、UMAP-DAGMM、SOM-UMAP-DAGMM模型效果如表8所示。

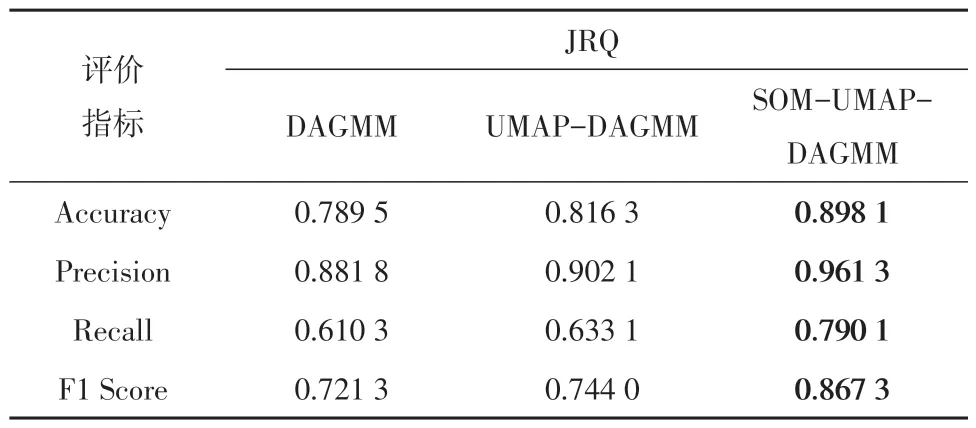
表8 JRQ数据集实验结果Table 8 Dataset experimental results of JRQ

在生产数据集FAN上，DAGMM、UMAP-DAGMM、SOM-UMAP-DAGMM模型效果如表9所示。

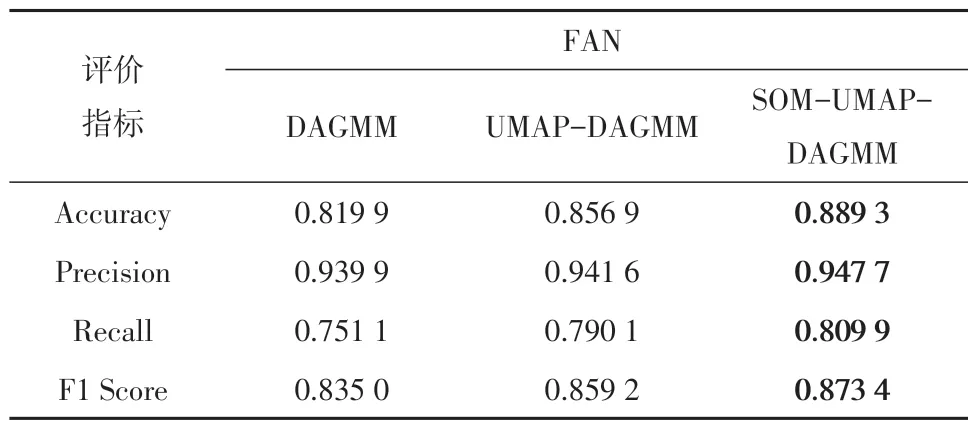
表9 FAN数据集实验结果Table 9 Dataset experimental results of FAN

在生产数据集NJSB上，DAGMM、UMAP-DAGMM、SOM-UMAP-DAGMM模型效果如表10所示。

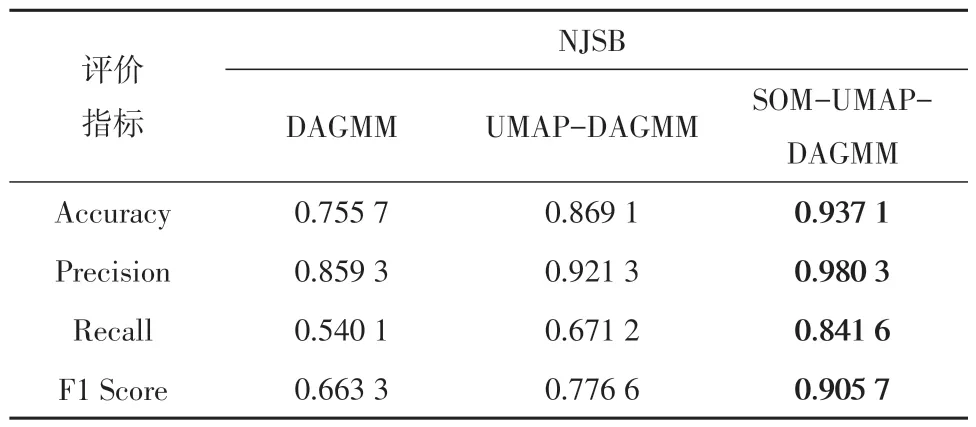
表10 NJSB数据集实验结果Table 10 Dataset experimental results of NJSB

从以上实验结果表中，可以看出在Arrhythmia 数据集上，UMAP-DAGMM的F1Score比DAGMM提高了0.131 7。在Thyroid 数据集上，UMAP-DAGMM 的F1Score比DAGMM提高了0.17。在3个生产数据集JRQ、FAN、NJSB 上，UMAP-DAGMM 的F1Score分 别 比DAGMM 提升了0.022 7、0.024 2、0.113 3；这也证实了UMAP 网络的加入确实能增加低维表示的高维信息，从而提高DAGMM的性能。

在3 个生产数据集JRQ、FAN、NJSB 上，SOMUMAP-DAGMM分别比DAGMM提升了0.146、0.038 4、0.242 4；比UMAP-DAGMM 提高了0.123 3、0.014 2、0.129 1。

同时SOM-UMAP-DAGMM 的性能在2 个公开数据集和3 个生产数据集中都是最好的，证明了SOM 强大的空间拓扑保存能力可以在UMAP-DAGMM的基础上进一步提升效果。

3 结语

本文针对在生产设备数据集上，针对DAGMM 高维信息不足导致性能欠佳问题，提出UMAP-DAGMM，通过在原来的损失函数上新增交叉熵与DAGMM联合训练，在维持端到端的训练模式下，补充了低维表达中的高维数据分布信息。为了进一步提升效果，提出SOM-UMAP-DAGMM，通过预训练SOM，再训练UMAP-DAGMM，继续补充空间拓扑信息。经过调参实验设置较优的参数后，UMAP-DAGMM 较DAGMM有所提升，SOM-UMAP-DAGMM性能最优。