基于优化扰动法的光伏发电系统最大功率控制方法的研究

赵东强

（大唐陕西发电有限公司延安热电厂，陕西 延安 716004）

0 引言

最近十年，光伏发电行业得到了迅猛发展，其在缓解能源危机和环境保护方面都做出了巨大的贡献。但现今光伏发电系统仍旧存在电池转换效率低、前期投资大以及发电成本高等缺点［1］；光伏电池由于其输出的电压和电流会随着日照强度和环境温度的变化呈现明显的非线性，因此，在实际应用环境中，光伏阵列输出功率呈现多波头，为了在同样的日照和环境温度下获得尽可能多的电能，就存在着一个系统最大功率输出点（MPPT-Maximum Power Point Tracking）的问题［2］。通过采用合理的控制算法，实现光伏发电系统工作在最大功率点是解决问题的措施之一。

本文按照控制理论的出发点以及MPPT控制方法的发展历程，对常用的控制方法进行了分类分析与总结，提出了一种基于优化扰动算法的MPPT，即依据光伏阵列的输出特性，确定阵列中可能出现的极值点位置，通过在局部极值点附近寻优确定极值点，最终通过比较极值点的功率大小，确定最大功率点。这种方法避免了陷入局部最优，并且只搜寻可能的极值点区域，具有较好的实时性。

1 光伏阵列最大功率点跟踪控制方法

在光伏阵列的实际工作中，由于环境因素的变化，会造成光伏阵列输出特性发生变化，其输出功率及最大功率点也会相应地发生改变，而且，试验分析认为光伏阵列输出电流受光照强度变化影响，而其输出电压受外界环境温度变化影响。早期时，光伏阵列MPPT技术研究主要有以下3 种：定电压跟踪法［3］（CVT）、光伏阵列组合法［4］、实际测量法也可以称为“模型建立法”［5］。随着光伏阵列容量的增大及近年来研究人员对光伏控制技术的进一步研究，现如今，对于光伏阵列最大功率的跟踪算法和控制精度都取得了长足的发展，目前的控制算法主要有以下3种，并且某些研究方向还在改进或研究当中。

1.1 基于优化数学模型的MPPT控制方法

此类方法以实物为基础建立数学模型，构造数学方程并且绘制模型特性曲线，最终求解光伏发电系统的最大输出功率点。因此，这种方法的光伏阵列的等效电路模型和各种参数的精确性直接影响光伏发电系统的控制性能。

1）开路电压比例法

根据光伏组件的输出特性分析得：运行环境（日照强度、温度）变化时，光伏组件的开路电压UOC与其最大功率点所对应的电压Umax呈现近似线性关系，可得式（1）：

式（1）中，k1为线性比例系数，并且其值小于1。

这种方法的优点是原理简单，不会产生振荡，并且通过简单模拟电路就可实现功能。比例系数k1的值根据组件参数的不同有所差异，其范围为0.71～0.80。为了获得较高精度通常采用断开光伏负载，求取开路电压UOC进而求得最大功率点Umax，但式（1）在原理分析推导时应用近似关系，造成计算值Umax并不是真正最大功率点电压，产生理论误差，除此之外，断开负载测量UOC本身存在功率损耗。

2）短路电流比例法

通过光伏组件的输出特性分析得：运行环境（日照强度、温度）变化时，光伏组件的短路电流IOC与其最大功率点所对应的工作电流Imax呈现近似线性关系，可得式（2）：

式（2）中，k2为小于1的线性比例系数。

这种方法具有与开路电压比例法相同的优缺点，除此之外，开路电流IOC的测量难度要大于UOC。

3）电流扫描法

电流扫描法是通过控制斩波占空比［6，7］，实现0～100%对应控制，测量太阳能电池板的电流和对应电压，从而通过DSP 计算获得光伏电池板的输出功率。再利用寄存器存在的功率值进行比较得出最大功率时，斩波的占空比，最后做到最大功率跟踪。这种方法由于要实现0～100%的占空比控制，因此，速度比较慢。

1.2 扰动观察法

扰动观察法也称为爬山法［8，9］，目前，此类MPPT控制方法在光伏发电系统最大功率跟踪研究中，研究较广，使用也比较普遍。基于扰动观察的控制方法直接根据光伏组件的输出电压和电流等信息进行控制，不直接考虑复杂的外界环境因素，可以简化控制系统［10-12］。此类方法采用给光伏组件的输出电压周期性增加扰动，根据其输出电压的变化趋势进而判断需要增加扰动方向，例如趋势未发生改变，则下一周期增加扰动方向不改变，若趋势发生改变，则附近存在最大功率输出点。此类方法的缺点是容易陷入局部最优，无法实现真正得到光伏最大功率跟踪。

1.3 电导增量法

电导增量法［13］是通过比较光伏阵列的瞬时电导和电导的变化量来实现最大功率跟踪。根据光伏阵列的P-U曲线可得式（3）：

即为功率最大点。

1.4 智能控制算法和非线性策略的MPPT控制方法

目前，包括模糊逻辑控制、神经网络算法和蚁群算法等在内的诸多人工智能控制算法及理论都已经在电气工程的各个领域得到广泛应用研究［13-17］。近些年，许多研究机构及高校将其应用在光伏阵列最大功率点跟踪控制方法中，并出现了许多具有实用价值的研究结果。以光伏阵列的非线性为出发点，中外众多研究人员在MPPT控制方法采用了非线性控制策略如单周控制、滑膜控制等，并最终获得最大功率［18-27］。

2 基于优化扰动法的MPPT算法

扰动观察法也称为“爬山法”。其工作原理为测量当前阵列输出功率，然后在原输出电压上增加一个小电压扰动分量后，根据增加扰动后的输出功率与扰动前的功率进行比较，即可获知功率变化的方向。如果功率增大就继续在扰动方向上增加扰动，如果功率减小则改变原扰动方向。扰动观察法结构简单、测量参数少、容易实现，因此广泛应用于光伏电池的最大功率点跟踪。其缺点是到达最大功率点附近后，会在其左右振荡，造成能量损耗，而且在实际运行中由于局部阴影等恶劣运行条件，会使得光伏板输出功率出现多峰现象，这样传统的扰动观察法会陷入局部最大功率无法实现真正的最大功率跟踪。

优化扰动法MPPT算法采用多极值函数全局优化方法，通过理论分析可能出现峰值的极值点的关系，定位可能出现的极值点位置，在其附近采用扰动法进行最大功率跟踪。因为每个潜在极值点都有可能是最大功率点。因此，在整个过程中，将电压分为3 个向量组：其中，可能出现极值点的位置表示向量v=(v1，v2…vi…，vn)，i= 1，2…，n；当前实际电压值表示为向量xi=(xi1，xi2…，xin)，i= 1，2…，n；搜寻过程中的最优点也就是实际极值点的电压向量为V=(V1，V2…Vi…，Vn)，i= 1，2…，n；搜寻过程中光伏阵列实际电压对应的输出功率向量为W=(W1，W2…Wi…，Wn)，i= 1，2…，n；在第i个极值点搜寻过程中，如果xik和xik-1所对应的功率W变化较大时调整量ΔU较大，当对应的功率W变化较小时，相应的ΔU较小，知道对应的功率W变化小于±5%，则确定这点为极值点电压。即N个光伏组件组成的光伏板可能出现N个极值点，每个极值点都与组件开路电压Uoc存在一定的线性比例关系，具体为第1 个极值点为0.8Uoc，第2 个极值点2*0.8Uoc，依次类推，N-1 个极值点为（N-1）*0.8Uoc，第N个组件的极值点为0.85*Uoc_M（Uoc_M为光伏板的短路电压，理论值为N*Uoc））。因此，可以确定所有需要搜寻的极值点。在每个极值点的搜寻过程中，根据功率的变换率，从而确定不同的占空比，做到功率变化较大时，占空比的调节量响应变大，功率变化较小时，占空比的调节量响应变小。以在第i个极值附近为例：

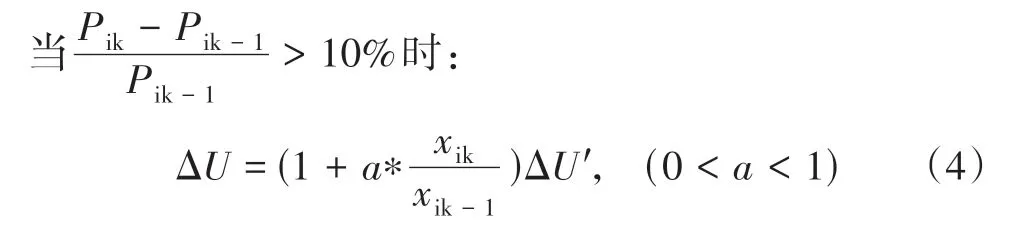
式（4）-式（8）中Pik为第i个极值点附近利用扰动法寻找第k次对应的功率，a为调节因子。

光伏发电系统MMPT控制中，目标函数值为测量的阵列输出功率。xi的位置代表阵列电压值，假设有n个组件，则搜索位置分别为阵列电压可能的极值点，由式（4）-式（8）得知，n阵列最多有n个可能的极值点，为了不丢失极值点，第1个粒子选为v1= 0.65 ×Voc，第2个粒子位置选为v2= 0.65 ×Voc+ 0.75 ×Voc，并依次类推，第n-1 个粒子位置选为vn= 0.65 ×Voc+(n- 1) × 0.75 ×Voc，当为第n个粒子位置选为vn= 0.8 ×VOC_MODLE。当进入程序，令BOOST开关管占空比D=0，获取组件开路电压Varry的值，而Voc=Varry/n。粒子电压搜索范围为0～vn。如主流程图图1系统首先获得组件开路电压Voc，阵列短路电压Varry，首先定义初始极值点电压v1=0.65 ×Voc，应用扰动法依次寻找极值点，并记录，当-5% << 5%时，则跳出循环，i+1进行下次局部寻优，最终获得所有极值点电压V=(V1，V2…Vi…，Vn)，i= 1，2…，n，依次比较极值点对应功率，获得最大功率，确定其对应占空比Dmax，退出程序。

3 仿真与实验

3.1 光伏阵列输出特性分析

引入LambertW 函数可以对光伏阵列输出电流和电压进行解藕可得式（9）、式（10）：

相同运行条件下M个相同参数的组件串联运行时可得式（11）：

则：IM=Im；VM=MVm。

同理，相同运行条件下N个相同参数的组件并联运行时则有：IM=NIm；VM=Vm。

相同运行条件下M个相同参数的组件串联，之后再与N个M相同参数组成的阵列并联所得的最大功率点有：IM=NIm；VM=MVm。因此，相同运行条件下相同参数组件串联运行时，只有一个极值点即最大功率点。

当组件参数不同进行串并联后，由于参数不一致，阵列输出功率公式中各项很难合并，无法直接给出各单体参数与并联后的新参数之间的关系，但光伏组件的极值点之间具有近似整数倍的关系。N 个阵列串联时出现的极值点最多有N个，且前N-1 个极值点之间存在整数倍关系，即Vi-1≈(N- 1)*Vm≈(i-1)K*Voc，第N个极值点VN≈K*VOC_MODLE，K的取值范围（0.7～0.85）。在串联了N个太阳能电池组件的支路中，当受到K个不同强度的入射光强照射时，组件的I-V 特性曲线将出现K个膝形，P-V 特性曲线出现K个峰。

3.2 仿真模型搭建

在Matlab/Simulink 软件中搭建了光伏模块采用5*5 阵列进行仿真实验。设置每一行的组件仿真温度，光照强度相同，仿真模型框图如图2 所示，其中光伏 组 件 的 基 本 参 数 为 ：ISC= 0.760 3 A，UOC= 0.574 V。

图2 光伏仿真模型框图Fig.2 Block diagram of photovoltaic simulation model

在仿真过程中，设置3 种情况，第一种情况：设置环境温度25 ℃，光照强度G1=1 000，G2=400，G3=600，G4=800，G5=1 200；第2种情况：设置环境温度25 ℃，光照强度G1=300，G2=500，G3=700，G4=900，G5=1 100；第3种情况：设置环境温度25 ℃，光照强度G1=420，G2=580，G3=750，G4=880，G5=1 000。在3 种情况下通过从小到大，线性连续改变负载得出光伏阵列的输出曲线如图3。

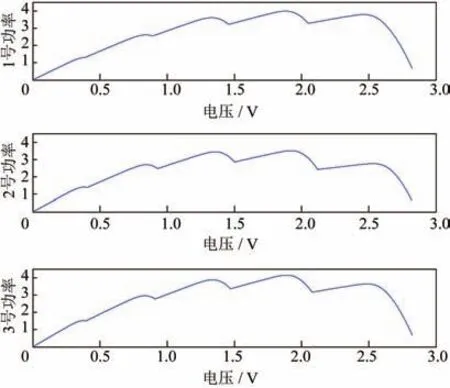
图3 光伏阵列的输出曲线图Fig.3 Output curve of PV array

根据表1 可得第1 种情况下：U1/Uoc=0.66；U2/Uoc=1.46；U3/Uoc=2.35；U4/Uoc=3.29；U5/5*Uoc=0.87。第2 种情 况：U1/Uoc=0.66；U1/Uoc=1.47；U1/Uoc=2.37；U1/Uoc=3.34；U5/5*Uoc=0.88。第3 种情况：U1/Uoc=0.67；U2/Uoc=1.47；U3/Uoc=2.31；U4/Uoc=3.27；U4/5*Uoc=0.85；与理论光伏模块前N-1个出现的可能极值点在（N-1）*0.8Uoc附近，第N个组件的可能极值点为0.85*Uoc_M相吻合。

表1 搜索区域初始位置参数表Table 1 Initial location parameters for the search zones

3.3 光伏阵列特性测试

进行优化扰动法的MPPT 仿真时，在Matlab/Simulink软件中搭建了光伏模块采用5*5阵列的Boost电路进行仿真实验，仿真模型图如图4 所示。仿真参数如下：BOOST 电路升压电感L=1 mH，阵列输入滤波电容C=5 µF，直流母线电容C1=50 µF，负载R=3 Ω。

如图4光伏阵列仿真模型，设置环境温度25 ℃，光照强度G1=1 000，G2=400，G3=600，G4=800，G5=1 200；负载R=3 Ω。系统0.006 s前，模型中BOOST电路开关器件占空比D=0；0.006 s-0.031 s模型中BOOST电路开关器件占空比D采用固定步长从0增加至1，从而获得固定负载时，光伏阵列的功率曲线，如图5所示，根据图5分析可得光伏阵列的最大输出功率Pmax= 4.130 1（W），D=0.46。

图5 5*5光伏阵列固有特性仿真结果Fig.5 Simulation results of 5*5 PV array inherent characteristics

3.4 基于优化扰动法的MPPT仿真分析

采用基于优化扰动法的MPPT仿真设置模型的工作参数相同，即设置环境温度25 ℃，光照强度G1=1 000，G2=400，G3=600，G4=800，G5=1 200；负载R=3 Ω。系统0.006 s 前，模型中BOOST 电路开关器件占空比D=0；系统0.006 s 时投入优化扰动法的MPPT 控制器，可得阵列的输出功率曲线如图6所示。根据基于优化扰动法的MPPT 算法原理可得，搜索区域共有5 个区域，区域的起始位置如表2 所示，在搜索过程中，根据截止条件，最终经过极值点对应功率比较确定第3 个极值点对应最大功率，其输出功率为Pm=4.094 W，对应占空比D=0.424 9，与实际最大功率4.130 1 W 相差0.036 1 W，相对误差0.8%。结果表明基于优化扰动观察法的最大功率跟踪法能够实现可靠的最大功率追踪，且效果较好。

表2 搜索区域初始位置参数表Table 2 Initial position parameters for the search zone

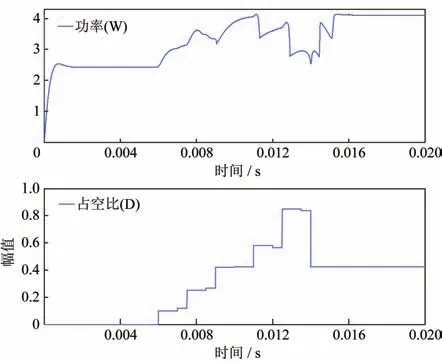
图6 5*5光伏阵列基于优化扰动法仿真结果Fig.6 Simulation results of 5*5 PV array based on optimal perturbation method

4 结语

本文通过对现有光伏发电系统MPPT控制方法的分析，提出了基于优化扰动搜索的MPPT控制方法，这种方法可以将搜索范围定位在多个可能的极值点附近，进行局部寻优，最后通过比较局部最优确定全局最大功率点。通过仿真验证，极端条件下阵列多波头运行时，此种算法仍能够准确地确定最大功率点；除此之外，这种方法原理简单，容易实现，能够避免传统扰动法易陷入局部最优的缺点，并且采用分区局部寻优，跟踪速度更快。