稳健的重尾线性赌博机算法
马兰霁弘 赵 鹏 周志华
(计算机软件新技术国家重点实验室(南京大学)南京 210023)
许多现实世界的应用可以被建模为面对不确定因素时的序列决策问题,其基本挑战是探索(exploration)和利用(exploitation)之间的权衡困境.多臂赌博机[1]是一种系统化模拟这类问题的模型,在该模型中,学习者每轮从摇臂池中选择1 个摇臂,随后从环境中收到选择的摇臂所对应的奖赏.学习者的目标是尽可能最大化所获得的累积奖赏,因此学习者必须在收集更多关于奖赏分布的数据(探索)和选择到目前为止最有可能取得最高奖赏的摇臂(利用)之间取得平衡.
随机线性赌博机是多臂赌博机在实际应用中的一个自然和重要的变体,已经引起了相当大的关注.其通常假设每个摇臂都具有其对应的d维特征,这些特征通常被称为“上下文信息”(contextual information),学习者需要根据上下文和所获得的历史奖赏信息来选择下一个摇臂.在第t轮中用xt表示所选摇臂的特征信息,该摇臂所能获得的奖赏可参数化为其上下文信息的线性函数,额外加上满足一定性质的噪声 ηt.其形式化为
其中θ ∈Rd是未知的回归系数,ηt是服从亚高斯分布的噪声.尽管该模型非常简单,但是它已被广泛应用于许多现实场景,如临床试验[2]和个性化推荐[3].
在现实世界的应用中,在线数据通常是从开放动态的环境中收集的,导致数据的不规范性经常出现,而这些不规范性又进一步限制了标准模型式(1)及其相应算法的使用.在本文中,我们特别关注2 类开放动态环境下经常出现的数据不规范性——分布变化(distribution charge)和重尾噪声(heavy-tailed noise).分布变化指的是摇臂的奖赏分布可能随时间变化,导致标准模型式(1)中的回归系数 θ随时间变化,这意味着根据以往的历史数据学习很可能得到一个对当前时刻有偏的模型;重尾噪声指的是标准模型式(1)中的噪声 ηt可能服从重尾分布,而不是统计性质良好的亚高斯分布,如金融市场投资的极端收益[4]和神经振荡的波动[5]等实际场景.这2 种数据不规范性使得传统的决策模型不再具有以往的独立同分布性质而难以分析.据我们所知,在线性赌博机问题上,目前还没有相应的算法能同时处理这2 个因素.
在本文中,我们研究了重尾线性赌博机算法(heavytailed linear bandits algorithm),名为RM-LinUCB,该算法同时对分布变化和重尾噪声具有稳健性.该算法由3 个关键部分组成:置信上界,用于解决序列决策问题中的探索与利用的平衡;均值中位数估计器,用于减少潜在的重尾噪声所引起的估计误差;重启策略,用于解决分布变化问题,当历史上下文和奖赏分布不符合当前数据分布时,定期重启并开始新的参数估计.在理论保障方面,对同时包含分布变化和重尾噪声的线性赌博机问题建立了遗憾下界,其结果表明:最坏情况下,存在某个特例使得任意算法的遗憾界至少为其中的物理含义是回归系数在总时间T中的累积变化,其反映了环境的动态变化程度.除此之外,我们对本文提出的算法进行了遗憾界分析,证明了该算法具有的遗憾上界保障,这意味着本文的算法所产生的遗憾界随总时间T是次线性的,即该算法产生的每轮平均遗憾将随总时间T的增大收敛至0,有时也称该算法是“无悔的”(no-regret).此外,该算法所产生的遗憾界包含了没有分布变化或重尾噪声情况下所产生的遗憾界.在此基础上,本文还设计了一个实用的技巧,使得本文的算法在缺乏对于数据不规范性的先验信息时仍能够应付未知的环境变化.最后我们在合成和真实世界的数据集上进行实验来验证算法的有效性.
1 相关工作
本节首先介绍随机线性赌博机的发展,然后就数据不规范的2 类问题(分布变化和重尾噪声)分别讨论一些相关的工作.
1.1 随机线性赌博机
对于随机线性赌博机问题的研究可以追溯到Naoki 等人[6]的工作.Dani 等人[7]首先建立了(稳态)线性赌博机问题的最小下限,表示对于时间长度为T、特征维度为d的随机线性赌博机问题,任意在线算法在该问题上都至少具有的遗憾下界;并且进一步设计了一种基于置信上界的算法,证明了其具有的遗憾上界,其中O(·)省略了与T相关的对数项.随后,Abbasi-Yadkori 等人[8]的开创性工作通过引入自归一化过程的分析技巧,大大简化了算法设计和遗憾分析过程,并证明了与Dani 等人[7]相同的(甚至在一些lnT阶更紧的)遗憾上界.该研究思路在后来的研究中[9-13]得到了积极的发展.更多关于随机线性赌博机的介绍,我们推荐读者参考该领域专著[14].
1.2 分布变化
传统机器学习依赖于环境封闭的静态假设,当环境发生动态变化时可能不够稳健[15-17].由于数据收集环境可能不断变化,在线数据的分布随之不断变化,这为在线学习技术带来了巨大的挑战.此问题已经引起许多研究者的关注,并尝试在一些具体的在线学习场景中处理环境变化带来的影响[18-24].Cheung 等人[25]对分布变化场景下的随机线性赌博机问题进行建模,并证明了该问题的最小遗憾下界为其中代表回归系数在总时间T内的累积变化,有时 PT又被称为路径长度(path-length).此外,Cheung 等人[25]提出使用滑窗最小二乘估计器来估计回归系数,并基于此估计进一步执行置信上界算法,证明了该算法具有的遗憾上界.通过使用加权最小二乘估计器[26-27]代替滑窗最小二乘估计器,Russac 等人[28]提出D-LinUCB 算法,在不存储历史数据的情况下得到了与Cheung 等人[25]相同的遗憾上界.D-LinUCB 的优势在于其是在线更新的,其劣势是需要计算较大的2 个协方差矩阵,计算效率不高.然而,Zhao 等人[29]指出文献[25,28]遗憾上界结果的理论证明中存在技术缺陷,导致其给出的遗憾上界实质上不成立.Zhao 等人[29]还提出了一种技术修补方案对遗憾上界进行重新分析,证明文献[25,28]算法的遗憾上界应修正为除此之外,Zhao 等人[29]还提出了一种新颖的基于重启策略的线性赌博机算法,该算法同样能够得到的遗憾上界保障,但在计算存储上更加高效,且理论分析也更加简洁.
1.3 重尾噪声
重尾噪声是指噪声服从一个具有有限1+ε阶中心矩的无界分布.Liu 等人[30]首先考虑带有重尾噪声的赌博机问题.Bubeck 等人[31]和Vakili 等人[32]分别表明 ε ≥1的条件足以使带有重尾噪声的赌博机问题恢复到与亚高斯噪声相同的遗憾界.因此,在带有重尾噪声的赌博机模型的研究中,大多数工作都集中在ε ∈(0,1]时的更为困难的情况.Hsu 等人[33]提出使用均值中位数估计器进行估计,其主要思想是统计多个采样平均值的中位数以避免极端离群值的干扰.Audibert 等人[34]提出截断策略,其思想是截断超过给定阈值的异常值以过滤极端离群点.在文献[33-34]的工作的基础上,Medina 等人[35]首先解决了ε ∈(0,1]时的重尾线性赌博机问题,实现了的遗憾上界.这个结果后来被Shao 等人[36]改进,达到了近似最优的遗憾上界随后,Xue 等人[37]将重尾噪声的处理拓展到有限摇臂场景的随机线性赌博机问题.
2 RM-LinUCB 算法
本节首先简述问题设定和本文提出的RM-LinUCB算法框架,然后详细介绍该算法中的3 个核心组件,即置信上界算法、均值中位数估计器和重启策略.
2.1 问题设定
本文关注同时具有分布变化和重尾噪声下的线性赌博机问题.在某个特定的时刻t,决策者根据上下文和历史奖赏信息选择一个摇臂,所选摇臂由其上下文信息xt∈Rd表示.决策者在某一轮通过摇臂xt所能获得的奖赏是yt随机线性赌博机的变体.
与标准模型式(1)不同的是,θt∈Rd是可能随时间变化的回归系数.我们假设回归系数的可行集被限定为
除此之外,与Dani 等人[7]工作的不同之处在于,仅仅要求噪声 ηt的1+ε阶矩有限(即满足重尾分布):
其中c∈(0,+∞).Vakili 等人[32]已经证明,当ε ≥1时,噪声分布的方差是有限的,因此与亚高斯噪声的情况一样具有相同的遗憾上界.因此,我们把重点放在ε ∈(0,1]的更困难的情况下.
分布变化使得流式数据不再满足独立同分布假设,这将使得重尾噪声场景下的线性赌博机问题极端困难、难以分析,特别是难以通过统计方式对重尾分布进行处理.我们对于流式数据的要求进行了适当的放松:本文中只考虑批量大小为B的小批量流式数据.假设同一个批次内的回归系数 θt保持不变,而θt将在不同批次之间发生变化,此假设在许多现实应用场景中都容易满足,例如可互换的专家系统[38]和季节性推荐系统[39].
参照文献[29]的研究,本文选择动态遗憾界作为评价算法的性能指标,其定义为
即将算法所获得的累计奖赏与一个能够获得回归系数全部信息的每轮最优策略的累积奖赏进行比较.与之相比较的是静态遗憾界,其将累计奖赏与动态遗憾界相比较.我们认为在开放动态环境中,将本文算法与可能变化的每轮最优策略作对比更为合理.
2.2 算法框架
本文所提出的算法框架如图1 所示,我们首先将一个批量大小为B的数据分割为长度为k的N=个列.在第p列开始时,首先根据置信上界算法选择一个摇臂xp,并在接下来的整个第p列,即t=(p-1)k,(p-1)k+1,(p-1)k+2,…,pk时,都选择这个摇臂共k次,并观察相应的奖赏.在第p列结束时,根据均值中位数估计器得到共k个估计θˆp,k,我们从中选择一个系数 θˆp作为回归系数的估计,并根据置信上界算法指导下一列,即第p+1列的摇臂选择.随着数据不断到达,当不同批次之间的数据分布变化过大时,我们认为历史数据对当前的学习任务已经没有帮助,因此将重启整个学习过程.
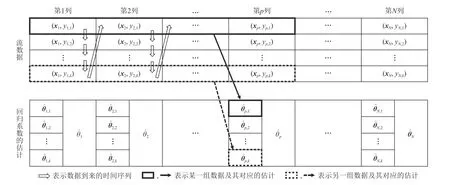
Fig.1 Illustration of RM-LinUCB algorithm.图1 RM-LinUCB 算法示意图
本文提出的RM-LinUCB 算法包含3 个组件:
1)均值中位数估计器(median-of-means estimator)解决数据分布存在重尾噪声的问题;
2)置信上界(upper confidence bound)算法处理赌博机问题中探索与利用的均衡问题;
3)重启策略(restart strategy)解决数据分布中存在的分布变化的问题.
2.3 均值中位数估计器
重尾噪声带来的主要困难体现在极端值的存在将使得数据整体没有很好的统计特性.为了减少由此产生的估计误差,基于Hsu 等人[33]和Shao 等人[36]的算法,我们使用均值中位数估计器来对回归系数进行估计.根据假设,回归系数在同批次内不变,算法以批次为基本单位来估计回归系数.如图1 所示,当某批次数据到达时,首先将该批次(共B轮)分为N=B/k列,每列含有k轮.在该批次的第p列开始时,算法首先选择一个摇臂xp.随后在第p列的所有k轮中,重复选择相同的摇臂xp共k次,并获得相应的奖赏反馈yp,1,yp,2,…,yp,k.在第p列的最后一轮决策之后,将得到k行、大小为p的历史数据,i∈[p],j∈[k],我们在图1 中用不同线型的加粗框表示不同行的数据及其估计.对每行历史数据,使用正则化最小二乘估计来估计回归系数,其形式化为
其中λ >0为正则化系数.上述方程的闭式解为
其中rj是和其余估计定义在Vp上距离的中位数:
随后,算法将根据置信上界算法选择下一列所使用的摇臂xp+1并重复此估计过程.
2.4 置信上界
均值中位数估计器估计了第p列所得到的回归系数 θˆp,在此基础上构建每个摇臂的置信上界作为摇臂选择的标准.根据面对不确定时乐观选择[8]的原则,选择摇臂池中拥有最大置信上界的摇臂作为第p+1列的摇臂,其形式化为
RM-LinUCB 的伪代码如算法1 所示:
算法1 中,βp为第p列的置信半径,其计算公式为
算法1 遵循过程:在第p列开始前,算法首先根据式(8)选择一个摇臂xp,然后在第p列的所有k轮中重复选择这个摇臂并获得相应的奖赏反馈;根据这些反馈,算法通过均值中位数估计器式(5)(6)对第p列的回归系数进行估计;算法通过式(9)计算置信半径以进行下一列,即第p+1列的摇臂选择.
2.5 重启策略(restart strategy)
为了处理模型在总共T轮上的分布变化,本文采用了带有固定重启参数H的重启策略.算法首先将总共T轮决策划分为T/Hk-1次重启,表示每进行Hk轮决策后就重启1 次.这意味着算法每隔H列就重启1 次学习过程.为了更好地简化所使用的重启策略,引入了一个新的变量M=H/N,M表示一个重启周期内的批次数,其中N=B/k是一个批次中的总列数.如果历史数据的批次数达到M,则表示算法已经进行了至少Hk轮决策,此时分布变化可能已经过大,本文算法选择重启学习过程重新对分布进行估计.此外,Zhao 等人[29]证明了一个固定的H足以保证无悔的性质,本文算法将H设为固定的超参数.
3 理论保证
本节首先建立了在分布变化和重尾噪声下的线性赌博机的遗憾下界,然后分析了所提出算法的遗憾上界,以验证所提出算法是无悔的.
3.1 问题的遗憾下界
首先根据定理1 建立了问题的遗憾下界,它描述了问题的难度,因为在最差情况下没有算法能比该理论极限做得更好.
定理1.对于任何T≥d,任何策略 π的遗憾都满足遗憾下界:
3.2 算法的遗憾上界
下面的定理2 表明,RM-LinUCB 具有无悔的遗憾上界,即每轮平均遗憾随时间T渐进收敛于0.
定理2.RM-LinUCB 在共T轮上的动态遗憾RT以至少1-δ的概率有
注1:将得到的遗憾上界与定理1 中的遗憾下界进行比较,可以看到它们存在一定的差距.然而,这个差距存在于所有处理分布变化的线性赌博机的算法中[25,28-29],本文的算法保证了重尾噪声不会让这个遗憾上界变得更差.
注2:当ε=1时,即重尾噪声退化到亚高斯噪声时,本文的遗憾上界为这与具有分布变化和亚高斯噪声的线性赌博机算法的遗憾上界[25,28-29]相同;当PT=0时,即没有分布变化时,现在设定重启系数H=T(即在分布变化不存在时不需要重启),定理2 中的遗憾上界退化为这与Shao等人[36]的最优遗憾上界相匹配;当ε=1,PT=0时,即当噪声服从亚高斯分布,且环境分布不发生变化时,上述遗憾上界为,这与随机线性赌博机最优遗憾界相同[8].
证明.首先,在算法RM-LinUCB 中,以n表示算法自上次重启以来的累计列数,而p表示批量数据的当前列数.由于以 θn表示第n列的真实回归系数,首先分析均值中位数估计器的估计误差.由式(2)(6)和柯西-施瓦茨不等式,可得
4 在线集成适应技术
第3 节分析了算法的遗憾上界.由定理2 可知,重启参数H在RM-LinUCB 算法中起着重要作用.然而,为了得到最小的遗憾上界,H的最优设置需要提前知道路径长度 PT的先验信息,即算法要提前得知回归系数 θt的累积变化,然而这在一些实际场景中是不可能的.本节针对该问题进一步提出了一种在线集成技巧以处理该问题.
我们注意到,在亚高斯噪声下拥有分布变化的线性赌博机中也出现了需要先验信息的问题.双层赌博机(bandits-over-bandits)[25]算法能够在一定程度上解决该问题.其主要思想是对H可能的最优取值进行多次猜测,并根据一定的概率选择其中的一个作为算法的超参数H运行原算法.在1 次重启后,算法可以根据收到的奖赏反馈对各个备选超参数进行其对应概率的调整,以便在重启后以更高的概率选择一个更好的超参数H.
具体来说,算法首先初始化参数:
其中K是备选参数的数量,J是备选参数H的集合,γ可视为更新系数,sj,i是与选臂概率有关的特殊参数,d,S分别是摇臂的维度和回归系数的模长上界.若用pj,i表示第j个备选参数在第i次重启后被选中的概率,算法首先通过式(14)计算pj,i:
随后,算法以概率pj,i为第i次重启选择H=Hj,随后用所选的参数H运行RM-LinUCB 算法,并在算法的下次重启前收到累计奖赏反馈yi.确保双层赌博机算法的一个非常重要的假设是,所获得的奖赏是大概率有界的,这与重尾噪声问题相矛盾.为了解决这个问题,将双层赌博机和截断策略[34]结合起来.具体来说,设置截断阈值为Q=2H,这意味着如果重启前的累计奖赏yi的绝对值超过Q就会被截断到Q,这样就可以得到有界的累计奖赏yi.最后算法通过式(15)更新参数.
我们将该在线集成技巧称为RM-LinUCB-TBOB,其伪代码由算法2 给出.
5 实 验
本节分别在仿真数据和真实数据集上进行了实验,以验证所提出算法在处理数据不规范时的有效性.此外,还研究了在第4 节中提出的在线集成算法的有效性.
5.1 仿真数据
我们首先在仿真数据上进行了实验,分别考虑了2 类分布变化环境和2 种重尾噪声的共4 种情况.1)对比算法.本文将提出的RM-LinUCB 与Lin-UCB[3],RestartUCB[29],MENU[36]进行比较.LinUCB[3]是为有亚高斯噪声的随机线性赌博机而设计的.在此基础上,RestartUCB[29]引入重启策略以处理分布变化的情况,而MENU[36]引入均值中位数估计器以处理重尾噪声.分布变化和重尾噪声的先验信息是已知的,即对于RestartUCB,根据分布变化的路径长度设置其最优参数设置对于MENU,我们将重尾噪声的参数化信息(ε,c)作为输入直接运行.
2)全局设定.在所有实验方案中,总轮数T=6000,摇臂的数量n=20.摇臂的特征从高斯分布N(0,1)中随机采样得到后按L=1进行归一化.此外,设定δ=0.1,正则化参数λ=1,回归系数最大模长S=1和特征维度d=2.最后的结果在100次独立实验上取平均数.
3)分布变化设定.按照Russac 等人[28]的实验设置创建分布变化.具体而言,构建了2 类环境变化,称为逐渐变化和突然变化.对于逐渐变化的环境,设定回归系数 θt在t<3000 时沿单位圆按逆时针方向从[1,0]变化到[-1,0],然后在t≥3000时在[-1,0]处保持静止;对于突然变化的环境,当t<1000时,设置基本参数θt=[1,0],然后当1000 ≤t<2000时 θt转移到[-1,0],2000 ≤t<3000时 θt转移到[0, 1],在最后的3000 轮中,θt保持在 [0, -1]的静止状态.此设定下的逐渐变化和突然变化对应的路径长度 PT分别是3.14和5.41.
4)重尾噪声设定.按照Shao 等人[36]的实验设置,在奖赏产生时添加的随机噪声 ηt由学生t-分布产生,ηt的2 阶中心矩的上界由自由度c所限制.具体来说,分别将标准学生t-分布的自由度设定为3和 10作为重尾噪声的2 种类型,其中t-分布的自由度越大,对应的重尾分布越明显.最后,将分布变化和重尾噪声两两组合,构建了4 种数据不规范场景,分别以场景S1~S4 表示,4 种场景的具体参数见表1.

Table 1 Four Scenarios of Simulation Data表1 仿真数据的4 种场景
4 种算法的每轮平均遗憾如表2 所示,同时,在图2 中展示了算法在场景S1~S4 的累积遗憾变化.在场景S3 和S4 中,当噪声类似于亚高斯噪声,即自由度c值较大时,RestartUCB 和RM-LinUCB 表现良好,而MENU 和UCB 则受到分布变化所带来的影响较大.在场景S1 和S2 中,即当噪声变得更加重尾时,RM-LinUCB 的结果更好,表明它在处理重尾噪声时具有更好的稳健性.总的来说,相较于RestartUCB,由于均值中位数估计器能够很好地处理重尾噪声,RM-LinUCB 对重尾噪声更加稳健.同时,相较于MENU,RM-LinUCB 对分布变化的稳健性更高.因此RM-LinUCB 在同时处理分布变化和重尾噪声时相较于处理单一情况的算法具有更高的稳健性.

Fig.2 The cumulative regret on scenarios from S1 to S4图2 S1~S4 场景下的累积遗憾
5.2 真实数据
现实数据集可能存在分布变化或重尾噪声等数据不规范现象,且难以处理.在本节评估了本文的算法在处理真实世界数据集时的整体表现.从StatLib和UCI 机器学习资源库[40]中选择了 6个基准数据集,即bolts,cloud,kidney,forestfire,slumptest,pokerhand.此外,还对Last.fm,Delicious[41],COMPAS[42]和30 天的Criteo 实时流量数据[43]这些规模较大的数据集进行了实验.
1)数据预处理.在处理原始数据时,按照Cesa-Bianchi 等人[41]的预处理来构建摇臂的上下文特征向量.具体而言,将样本的特征作为摇臂的上下文特征,然后通过PCA 降维后进行归一化处理,使所有实例的特征向量满足x2≤L=1.
2)构造赌博机问题.用预处理过的特征向量和它们的标签构造赌博机问题:每个样本数据都被视为一个可选摇臂,其标签是其对应的奖赏.总共的时间跨度T=10000.在每一轮中,通过随机选择1 个非零标签(奖赏)的样本,然后随机选择其他24 个样本来构建1 个可选摇臂池,这样每个摇臂池都应至少包含1 个具有非零奖赏的摇臂.因此,对于所有的数据集,摇臂池的大小被固定为25.此外,与仿真数据实验中相同,δ=0.1,λ=1,S=1.表3 中列出了数据集的特征维度(摇臂的上下文特征维度d)和样本(摇臂)总数.
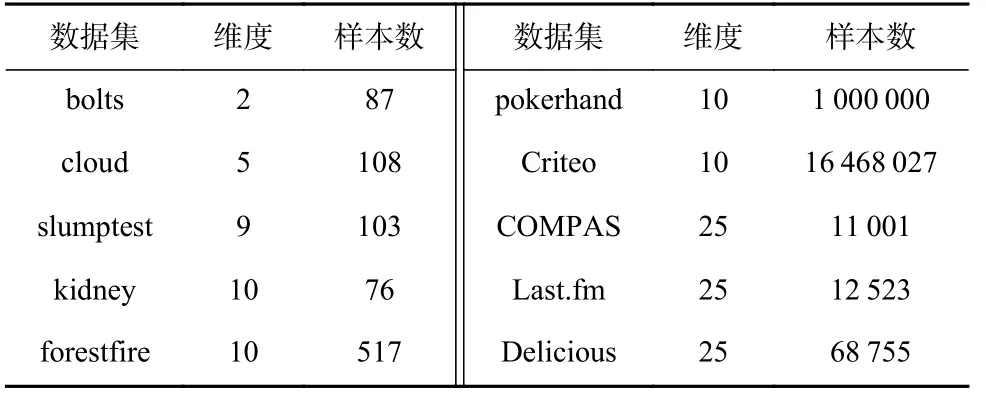
Table 3 Statistics of Real-world Datasets表3 真实数据集统计信息
3)对比算法.与之前的合成数据实验不同,在处理真实世界的数据集时,故没有任何关于重尾噪声或分布变化的先验信息,因此所有算法的参数都是通过网格搜索进行微调的.此外,因数据不规范对LinUCB 的影响较大,故省略了LinUCB 的结果.
4)实验结果.我们参照Zhao 等人[27]的实验设计,对RestartUCB,LinUCB 和RM-LinUCB 进行稳健性分析(robustness analysis).首先给出赌博机算法 A的稳健性(robustness)的定义:
其中CP(A)是算法 A的平均累积奖赏.对于最佳算法,有r(A)=1,而其他算法则满足r(A)<1.算法的稳健性总和越高表示整体性越好.
如图3 所示,RM-LinUCB 在10 个数据集上获得的稳健性总和为9.94,在所有对比算法中获得了最高的稳健性,从而验证了其在处理具有数据不规范性的真实世界数据时的稳健性.此外,通过仔细观察结果,可以得到更多有趣的结论.RM-LinUCB 和Restart-UCB 在bolt,cloud,forestfire 上的表现都优于MENU,这意味着在这些数据集上,MENU 受到了潜在的分布变化的影响.同时,RM-LinUCB 和MENU 在Last.fm和COMPAS 上的表现都优于RestartUCB,这意味着RestartUCB 收到了潜在的重尾噪声的影响.最后,RMLinUCB 在pokerhand 上的表现远远优于RestartUCB和MENU,验证了分布变化和重尾噪声同时存在于该场景中.

Fig.3 Robustness analysis图3 稳健性分析
5.3 在线集成适应技术
本文介绍了一种能够在重尾噪音下有效适应未知环境变化程度的在线集成技术.本节将验证所提出算法的有效性.
1)实验设定.采用与仿真实验情景S2 相似的环境,唯一的区别在于,总轮数T=10000,回归系数 θt在单位圆上以1 000 轮为间隔随机变化.
2)对比算法.将TBOB 与其他算法进行对比:
①当算法事先知道分布变化时间时,每当回归系数变化,该算法都会重新启动RM-LinUCB,我们称之为Oracle;时,以最佳参数
②若提前得知关于路径长度 PT和 ε的先验知识运行RM-LinUCB,我们将该算法称为Prior;
③当不知道关于路径长度 PT的先验知识时,从式(11)中随机猜测参数H并运行RM-LinUCB,我们称之为Guess.
3)实验结果.如图4 所示,各条曲线为对应的算法在100次独立实验上的平均遗憾.可以看到,所提出的TBOB 远好于Guess;即使不需要关于路径长度PT的先验知识,TBOB 的表现依旧与Prior 非常接近,这证明了TBOB 在缺乏对数据不规范的先验信息时仍能对环境有较强的稳健性.

Fig.4 Regret generated by TBOB图4 TBOB 所产生的遗憾
6 结 语
本文研究了有分布变化的重尾线性赌博机问题,其中噪声可能是重尾的,并且描述奖赏分布的回归系数可能随时间变化.针对该问题,我们首先建立了的遗憾下界以表征学习问题的难度.进而提出了一种新的基于置信上界的赌博机在线算法,其核心在于均值中位数估计器以应对重尾噪声的干扰,使用自适应重启策略以处理环境可能的分布变化.理论上,我们证明了该算法具有的遗憾上界,因而本文算法的每轮平均遗憾随时间T增大渐进收敛至0.此外,我们进一步设计了在线集成算法来应对数据不规程度未知的场景,得到的新算法仍然能够选择较好的参数以保持稳健性.最后,我们在仿真数据和真实数据上进行了实验,验证了所提出的算法在应对潜在的分布变化和重尾噪声时具有稳健性.
作者贡献声明:马兰霁弘负责论文相关文献调研、算法设计、理论推导、实验设计和论文撰写;赵鹏负责对算法的分析方法提供指导和修正,并辅助修订论文;周志华负责对论文的总体规划进行设计,指导整体研究方向.

