KdV-Burgers方程的一类新本性并行差分格式*
潘悦悦, 杨晓忠
(1.华北电力大学 控制与计算机工程学院, 北京 102206;2.华北电力大学 数理学院 信息与计算研究所, 北京 102206)
0 引 言
KdV-Burgers方程是一种带阻尼的KdV方程模型,也是一个典型的非线性波动方程.其一方面,可以描述同时含有色散、非线性水平对流、黏性流体的浅水长波的传播过程[1-2];另一方面,可以用来描述同时含有色散和耗散的等离子物理中的一些重要物理现象[3-5].KdV-Burgers方程求解的快速算法一直是计算数学研究的热点问题,其高效数值解法具有重要的科学意义和应用价值.
随着越来越多大规模科学计算问题的出现,人们开始对串行计算程序的合理化和并行化进行深入研究.近年来的大多数并行差分方法是条件稳定的,或者是无条件稳定但精度只有一阶.为了得到稳定性条件更宽松、计算精度更高的并行方法,实现串行差分方法的合理并行化,一种新的高效并行方法是必不可少的.针对抛物型方程,Evans和Abdullah[6]提出了分组显式(group explicit,GE)的思想,设计出交替分组显式(AGE)差分格式.通过计算网格区域中的两个相邻点,将得到的隐式方程转化为显式方程.交替使用这种方法,截断误差项可以部分抵消,从而提高了算法的精度.
隐格式具有良好的稳定性,但不适合并行计算.受到构造AGE方法的启示,张宝琳等[7]提出了用Saul’yev非对称格式构造分段隐式的思想,并且恰当地使用交替技术建立了多种交替分段显-隐式(ASE-I)和交替分段Crank-Nicolson(ASC-N)并行方法,得到了稳定性和并行性兼顾的研究成果.周毓麟院士[8]将最一般的抛物型方程的显隐混合格式称之为具有并行本性的差分格式,对其差分解的存在性、唯一性、收敛性和稳定性等理论问题进行了研究,建立了抛物方程并行本性差分方法的基本理论.现在,并行本性差分方法已经推广到很多发展方程的数值求解中[9-10].
王文洽[11]使用一组非对称格式构造了具有本性并行的ASC-N差分格式,求解了KdV方程,给出了线性绝对稳定性的理论分析.Yuan等[12]针对非线性抛物型方程组提出了一类无条件稳定,空间二阶精度的并行差分格式.Borhanifar和Abazari[13]应用无条件稳定的差分格式求解了电报方程.数值算例表明了新方法的稳定性和准确性.针对四阶抛物型方程,Guo和Liu[14]给出了经典的显式、隐式和C-N格式,主要分析了格式的无条件稳定性.Namjoo等[15]提出了广义Burgers-Fisher方程的3种格式:两种精确有限差分格式和一种非标准有限差分格式.通过误差分析,验证了该格式的精确性和有效性.Xue和Feng[16]建立了求解抛物型方程的有效算法.在第n层使用两种区域分解法,两种方法的解取平均值,得到第n+1层的解.该方法保持了并行性和稳定性.并行本性方法既适用于并行计算,又是无条件稳定或线性稳定的.然而,这些方法误差稍大,精度较低[17-18].
受到上述差分方法的启发,本文结合经典的显式、隐式和C-N格式,提出了一种求解KdV-Burgers方程的新并行差分方法.MASC-N方法具有更精确的结果和更宽松的稳定性条件.理论分析和数值算例表明,MASC-N格式线性绝对稳定,收敛阶为二阶.本文格式的计算效率远高于C-N格式的计算效率,新方法对于求解KdV-Burgers方程是高效合理的.
1 KdV-Burgers方程的混合交替分段C-N差分格式
1.1 KdV-Burgers方程
KdV-Burgers方程的一般形式为[1-2]
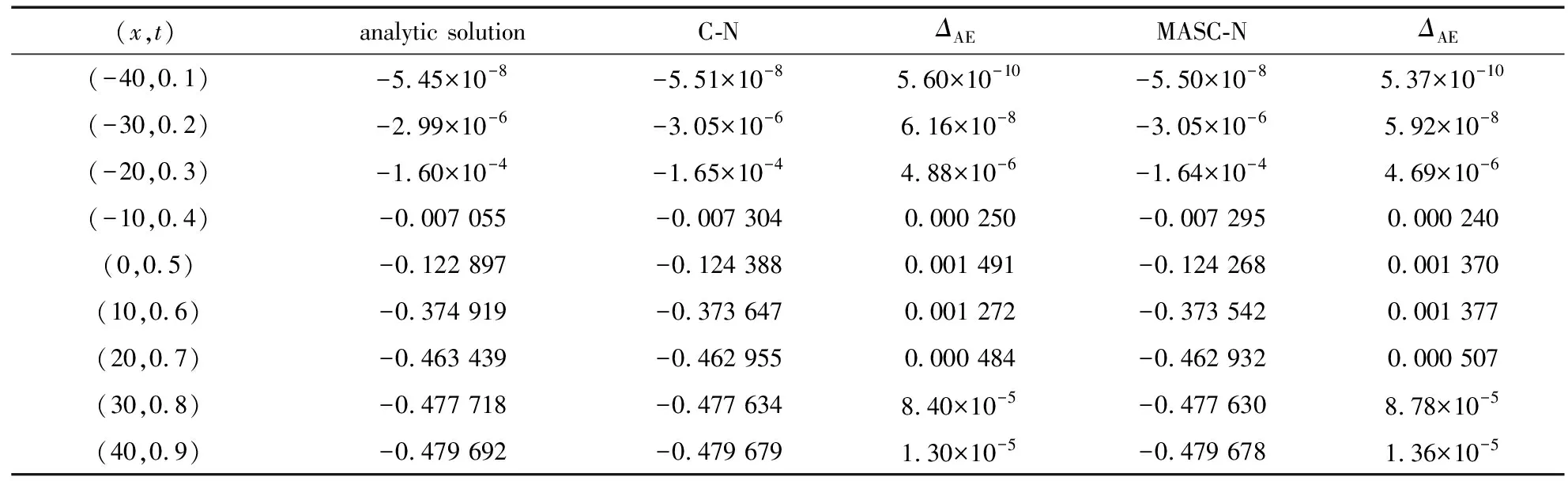
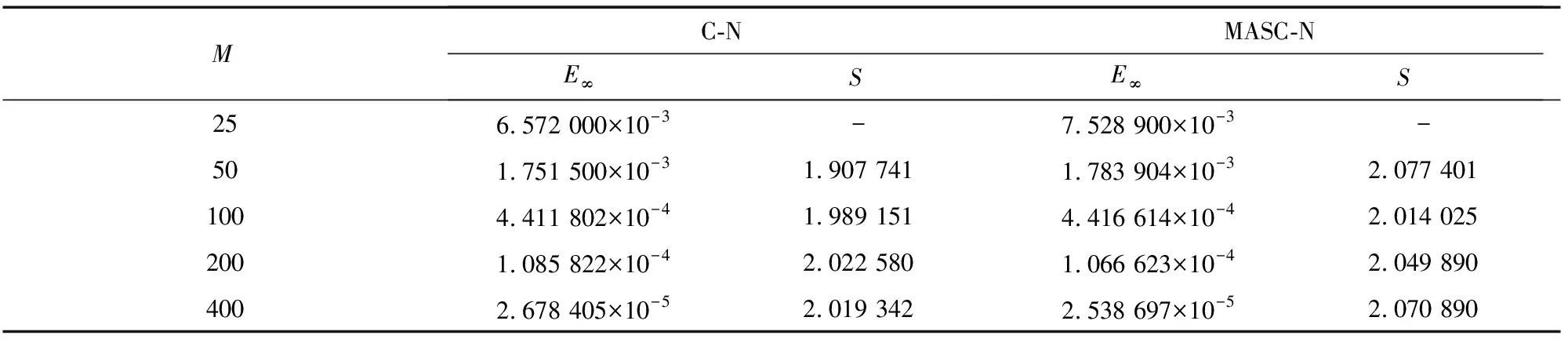
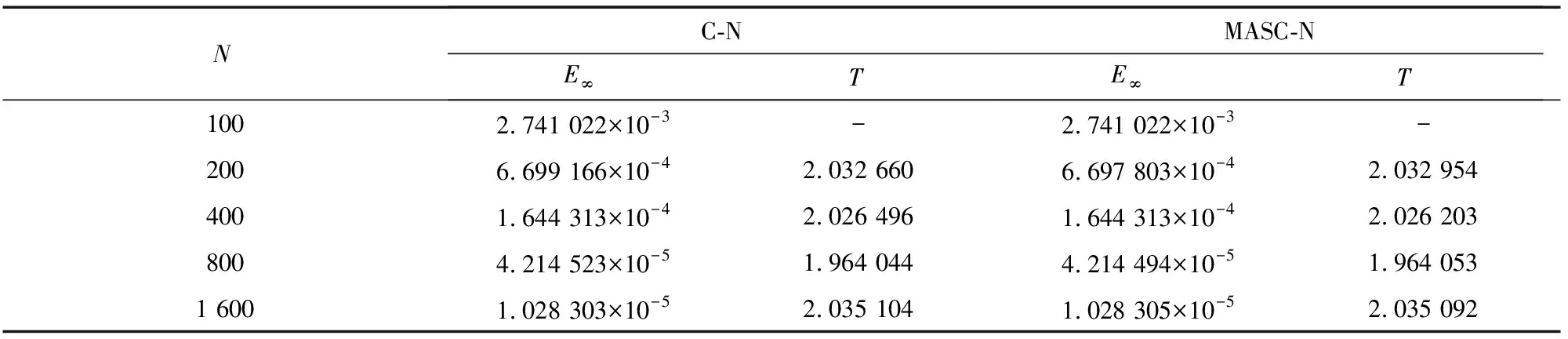
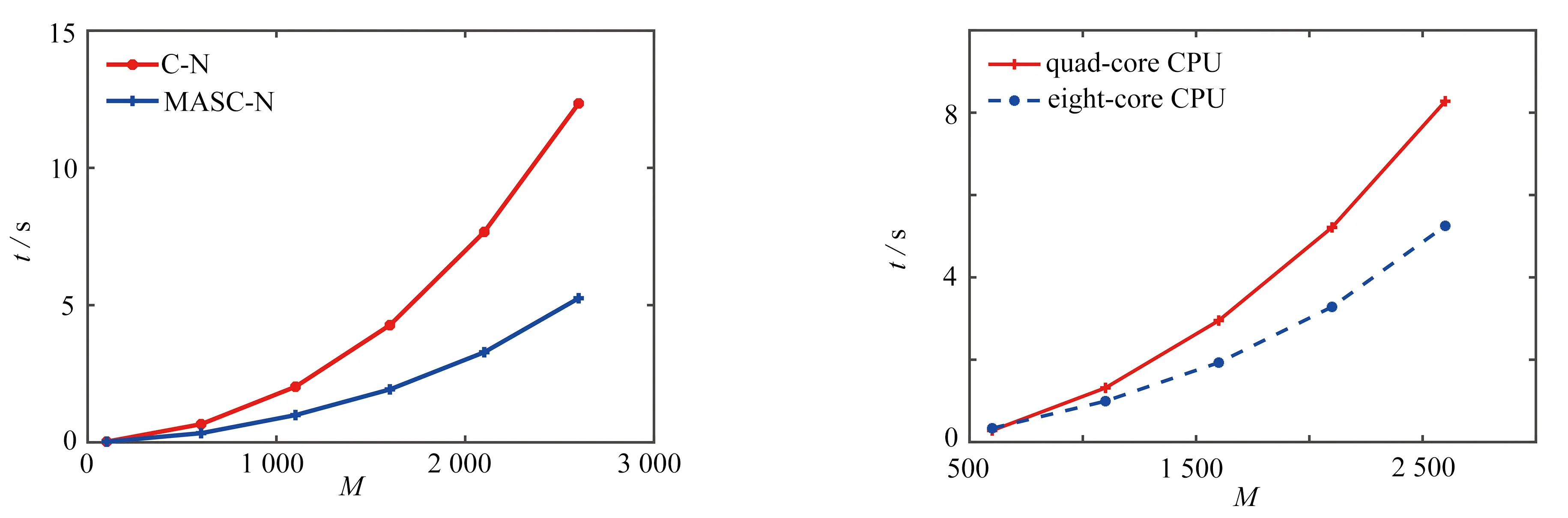
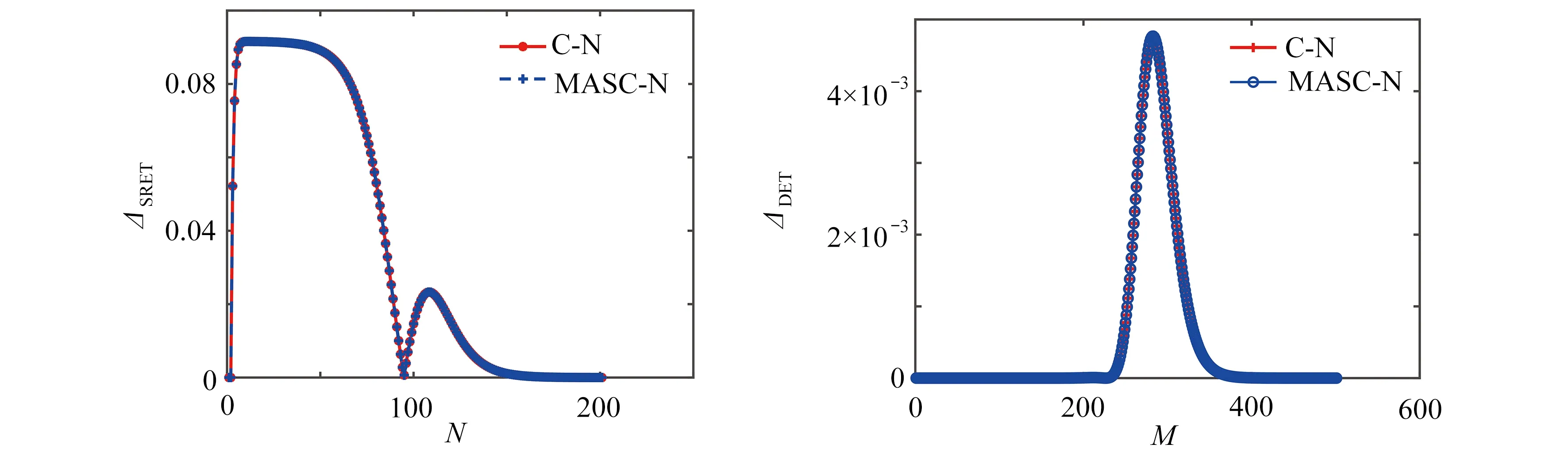
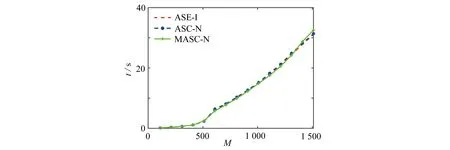
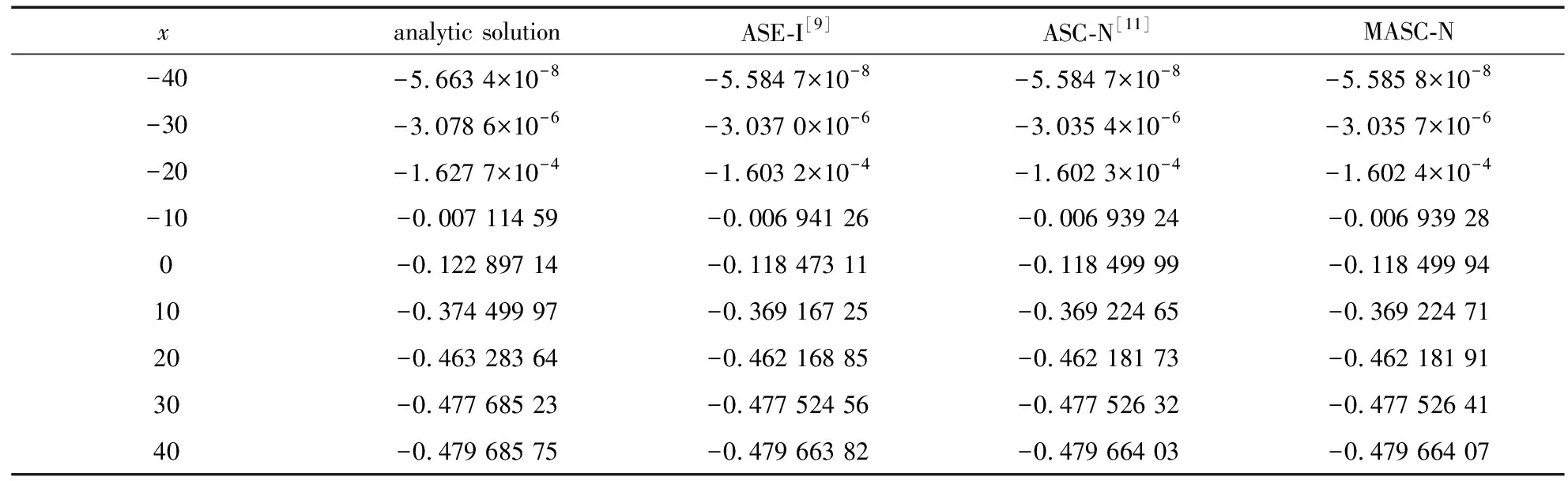
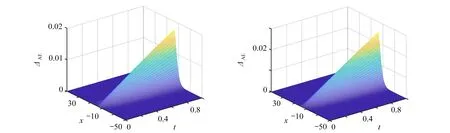
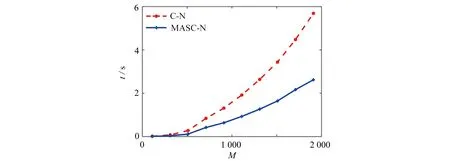
ut+αuux+βuxx+εuxxx=0,L1 (1) 其中α>0,β<0,ε>0.初始条件和边界条件为 u(x,0)=f(x),L1≤x≤L2, (2) u(L1,t)=g1(t),u(L2,t)=g2(t), 0 (3) 其中L1,L2都是适当大的数. 以下是方程(1)的显格式、隐格式和C-N格式: (4) (5) (6) 其中 现在讨论KdV-Burgers方程的交替分段并行差分格式,本文的MASC-N格式(图1)将结合以上几种差分格式使用. 图1 MASC-N格式构造示意图 (7) 式中 Un,F1,F2是M-3维向量,I是M-3阶单位矩阵,A1和A2均是M-3阶对角矩阵,且满足A1+A2=I,A1=diag(θ1,θ2,…,θM-4,θM-3), 引理1(Kellogg引理)[19]设θ>0,矩阵G+GT是非负定的,则(θI+G)-1存在,并且有 ‖(θI+G)-1‖2≤θ-1. 引理2 MASC-N格式的A1G和A2G是非负定矩阵. 其中c<0.显然A1G+(A1G)T是弱对角占优矩阵,对角线上的元素是非负实数.因此A1G+(A1G)T是非负定矩阵,A2G+(A2G)T也是非负定矩阵,则A1G和A2G是非负定矩阵. 由初始条件得,U0已知,假设U2n已知,求U2n+1.由式(7)得到求解U2n+1的公式为 (I+A1G)U2n+1=(I-A2G)U2n+F1. (8) 显然,等式右边已知,(I+A1G)-1存在,式(8)有唯一解.同样地,使用MASC-N格式计算2n+2层的点: (I+A2G)U2n+2=(I-A1G)U2n+1+F2. (9) 同理可得式(9)有唯一解,定理得证. 定理1 KdV-Burgers方程MASC-N格式(7)的解是存在且唯一的. 引理3[19]设θ>0,矩阵G+GT是非负定的,则‖(θI-G)(θI+G)-1‖2≤1. 定理2 KdV-Burgers方程的MASC-N格式(7)是线性绝对稳定的. 古典显格式为 古典隐格式为 由图1可知,在每段的“内点”使用C-N格式,其计算精度为二阶.在每段的“内边界点”使用古典显式和古典隐式,计算精度为O(τ+h2τ+h2).在T1(τ,h)和T2(τ,h)的表达式中,分别包含了绝对值相同但符号相反的项.古典显式和古典隐式在每一时间层交替使用,部分项将相互抵消.因此,MASC-N格式的计算精度近似为二阶. 定理3 KdV-Burgers方程的MASC-N格式(7)的计算精度为O(h2+τ2),内边界点的计算精度为O(τ+h2τ+h2). ‖en+2‖≤‖(I+G2)-1(I-G1)(I+G1)-1(I-G2)en‖+ ‖(I+G2)-1(I-G1)(I+G1)-1Rn+1‖+‖(I+G2)-1Rn+2‖≤ C′n+2(τ2+h2). 定理4 KdV-Burgers方程的MASC-N格式(7)是收敛的. 为了验证理论分析,给出数值算例证明MASC-N格式的计算精度、稳定性、收敛性和并行性.同时给出MASC-N格式与ASE-I格式和ASC-N格式的比较试验、MASC-N格式扩展到mKdV-Burgers方程的数值试验. 例1 令ε=1,γ=1,μ=1,考虑以下KdV-Burgers方程[20-21]: ut+εuux-γuxx+μuxxx=0, -50≤x≤50, 0≤t≤1. (10) 初始条件为 边界条件为 解析解为 取时间层N=500,空间层M=500,图2和3分别给出了式(10)的孤立波解从时间t=0到t=1的精确解和MASC-N格式解的波形图.从图中可以看到,数值结果稳定可靠,保持了与精确解几乎完全一致的波形. 图2 精确解的波形 图3 MASC-N格式解的波形 表1 两种格式解相对于解析解的绝对误差 以下给出C-N格式和MASC-N格式收敛阶的数值试验.在点(xi,tn)处,定义误差E∞(h,τ)、空间收敛阶S和时间收敛阶T[22-23]: 令M=25,50,100,200,400,N=500和N=100,200,400,800,1 600,M=100,表2和3分别给出了C-N格式和MASC-N格式的空间和时间精度.由表中数据可知,两种格式的空间和时间精度为二阶.因此本文MASC-N 格式和已有的C-N格式有相同的阶数,数值试验结果与理论分析相符. 表2 两种格式的空间收敛阶 表3 两种格式的时间收敛阶 定义加速比Sp=T1/Tp和效率Ep=Sp/p[24],T1和Tp分别是C-N和MASC-N格式的运行时间,p是处理器的数量.使用八核处理器,令N=1 000,M=600,1 100,1 600,2 100,2 600,计算结果见表4.表4表明当M增加时,两种格式的运行时间都增加.但与C-N格式相比,MASC-N格式的运行时间增加缓慢.Sp和Ep都逐渐增加.随着M的增大,MASC-N格式的效率大幅度提高.当M>600后,MASC-N 格式的运行时间比C-N格式节约56%. 表4 两种格式运行时间的比较 图4给出了C-N和MASC-N格式的计算时间.可以看到C-N格式的计算时间迅速增加,变化率大.本文构造的MASC-N格式的计算时间更少,且变化率小.C-N格式是串行格式,通过LU分解计算5对角方程.但使用MASC-N 格式计算时,全局问题被分解成多个不相关的问题同步进行计算.程序循环有效地提高了计算效率,缩短了计算时间.从时间的角度来看,MASC-N格式具有明显的优势. 图4 C-N和MASC-N格式的计算时间 图5 不同CPU核数的MASC-N格式计算时间 图5给出了MASC-N格式在四核和八核CPU下的计算时间.可以看到随着空间网格数的增加,八核CPU的计算时间比四核CPU更少,MASC-N格式并行性明显. 为了验证MASC-N格式的稳定性和精度,给出随时间和空间变化的相对误差.定义时间层相对误差和(the sum of relative error for every time level,SRET,ΔSRET)与误差能量(difference total energy,DTE,ΔDTE): 取N=200,M=200,图6表明当N增加时,两种格式解的ΔSRET迅速减小,且趋向于0.因此,MASC-N方法求解KdV-Burgers方程是计算稳定的. 图6 C-N和MASC-N格式解的SRET 图7 C-N和MASC-N格式解的DTE 取N=500,M=500,从图7可以看出两种格式ΔDTE的最大值是5×10-3.表明两种格式数值解与解析解非常接近,误差很小,MASC-N方法有良好的计算精度. 例2 令L=100,T=1,考虑以下KdV-Burgers方程[25]: ut+uux-uxx+uxxx=0. (11) 初边界值由解析解给出,解析解为 比较3种并行格式的计算时间.固定时间层N=10 000,计算结果见图8和表5.ASC-N格式有最长的运行时间.ASE-I和MASC-N格式运行时间相似且MASC-N格式计算时间略短. 表5 3种并行格式的计算时间 图8 3种并行格式计算时间比较 比较解析解和ASE-I[9]、ASC-N[11]、MASC-N格式解.令N=210,M=210,t=0.5,表6给出了计算结果.表中数据表明3种格式的数值解相似,且MASC-N格式解最接近解析解. 表6 数值解和解析解 最后,取计算精度的权重为0.6,计算时间的权重为0.4.根据计算精度和时间比较3种并行格式,见表7.可以看到,MASC-N格式的加权排序总和数最小,可知其具有最好的性能和实用性. 表7 3种并行格式的比较 例3 令β=-1,ε=-1,考虑以下mKdV-Burgers方程[26-27]: ut+u2ux+βuxx+εuxxx=0, -50≤x≤50, 0≤t≤1. (12) 初边界值由解析解给出,解析解为 令N=210,M=210,t=0.5,表8为mKdV-Burgers方程解析解和两种格式数值解的比较.可以看出C-N格式解和MASC-N格式解几乎相同.图9和10分别是C-N和MASC-N格式的绝对误差,对比发现两种差分格式绝对误差最大值的级数为10-2. 表8 数值解和解析解 图9 C-N格式解的绝对误差 图10 MASC-N格式解的绝对误差 令时间层N=1 000,图11是C-N和MASC-N格式的运行时间.可以看到C-N格式的运行时间远大于MASC-N格式的运行时间.与C-N格式相比,MASC-N格式求解mKdV-Burgers方程更为高效. 图11 C-N和MASC-N格式的运行时间 KdV-Burgers方程的MASC-N并行差分格式是线性绝对稳定的,格式解存在唯一,与C-N格式的收敛阶同为二阶.在保证计算精度的前提下,MASC-N格式比C-N格式有更高的效率.与ASE-I和ASC-N格式相比,MASC-N并行差分格式对求解KdV-Burgers方程有更好的性能.同时,将MASC-N并行差分格式扩展到求解mKdV-Burgers方程,本文的数值试验结果表明,MASC-N格式的计算效率明显高于C-N格式的计算效率,MASC-N 格式求解各种类型的并行计算系统是有效的. 致谢本文作者衷心感谢德国阿尔弗雷德韦格纳研究所Sergey Danilov教授和王强博士在写作过程中提出的宝贵建议和意见;同时衷心感谢华北电力大学国内外联合培养博士生项目(2020)对本文的资助.1.2 MASC-N并行差分格式的构造
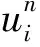

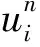
2 MASC-N并行差分方法的数值分析
2.1 MASC-N格式解的存在唯一性
2.2 MASC-N格式的线性绝对稳定性
2.3 MASC-N格式的收敛性

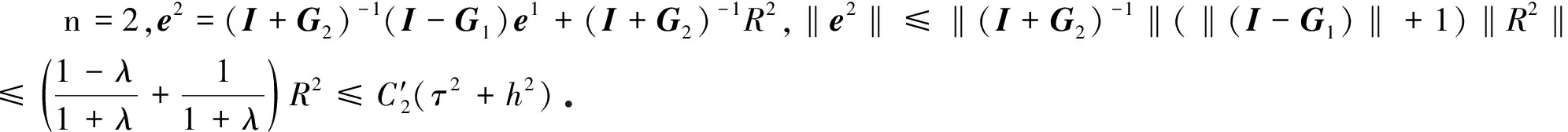
3 数 值 试 验

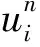




4 结 论

