微分求积法求解悬臂L梁固有振动特性研究*

李智超, 郝育新

(北京信息科技大学 机电工程学院, 北京 100192)

0 引 言

相比于常见的悬臂直梁结构,悬臂L梁结构由于其柔性更大、可设计性更强、空间利用更充分、振动过程中变形方式更多样等优点,被广泛投入到工程应用中,尤其是近年来作为压电俘能结构的主体而倍受关注与研究.在这些研究中,Chen等[1]以悬臂L梁为研究对象,研究了其2∶1内共振及其幅频响应特性,继而研究了如何改善其作为能量泵时的带宽,并研究了L梁参数对带宽的影响.Erturk等[2]提出了一种新型L型梁-质量可调结构作为压电能量收集器应用于无人机起落架,通过使结构前两阶固有频率相对接近,从而实现在更宽的频带内收集更多的能量.Harne等[3]提出的L型梁振动能量收集系统可以在谐波激励条件下利用1∶2内共振与饱和现象来提高能量转换性能,即使输入振动包含高水平的附加白噪声.Li等[4]研究了几何和材料特性对L型梁压电俘能器响应的影响,证明了考虑非线性效应时有助于提高在外激励振幅较大和强电场条件下俘能器性能的预测精度.Kim等[5]提出并研究了一种由悬臂梁和刚性臂组成的频率可变的L型能量采集器,该梁的特点是两根梁都水平放置,他们还深入研究了刚性梁的长度对系统固有频率的影响,并研究了该能量采集器的输出电压特性.

值得注意的是,在这些关于L型梁压电俘能应用的研究中,往往用到了悬臂L梁结构的内共振关系.因此,对L梁结构的固有振动特性进行深入研究,得到L梁各参数对其固有振动特性的影响规律,对其作为压电俘能结构的设计与应用具有重要的指导意义.

虽然运用有限元软件可以得到悬臂L梁结构的固有振动特性,但是不便于我们研究影响其固有振动特性的机理,因此有必要建立悬臂L梁的固有振动动力学模型,从理论上对其固有振动特性进行研究.自Bert等[6]首次将微分求积法投入结构力学求解与分析中起,该方法便已成为除Galerkin法、Rayleigh-Ritz法、拟谱法等传统空间离散方法外的又一高阶偏微分方程近似求解方法[7-8].其优势在于可以直接得到系统在物理空间中的解,而不是模态空间.Wang[9]和Tornabene等[10]将近年来微分求积法与微分求积单元法的最新进展做了详细的总结,列举了多种插值基函数的选取方式,讨论了多种边界条件的施加方法,并比较了各种方法的适用情况和优缺点.在实际应用方面,夏雨等[11]采用微分求积法研究了4种边界条件情况下等截面梁与变截面梁的内力和位移,并获得了变截面轴向功能梯度Euler-Bernoulli梁若干低阶固有频率.葛仁余等[12]利用微分求积法理论将变系数常微分控制方程转化为标准型的广义代数特征值问题,并提出了一种令节点呈等比数列分布的方法,以研究变截面轴向功能梯度Timoshenko梁的屈曲临界荷载.Khakpour等[13]利用三阶剪切变形理论,研究了热环境下弹性基体简支功能梯度多孔梁的固有频率,并使用了微分求积法对控制方程进行离散.Peng等[14]研究了预压缩梁横向自由振动的固有振动特性,将微分求积法直接应用于修正后的横向自由振动控制方程,求得固有频率的数值解.近年来,有学者还将微分求积法的应用范围延伸至二维板、壳、盘型结构振动领域.Szekrényes[15]采用微分求积法对分层复合板进行了数值模拟,解决了一些具有简单支撑和刚性固定边缘的包含材料缺陷的板问题.Liu等[16]采用修正偶应力理论(MCST),对层合旋转微系统进行了频率模拟和临界角速度模拟,并利用二维广义微分积分方法求解了各种边界条件下的非经典控制方程.Al-Furjan等[17]研究了具有蜂窝芯、两层含有SMA纤维的中间层和两层MHC外层的夹层盘的频率响应,根据Hamilton原理,运用广义微分求积法推导并求解了该结构的动力学方程.刘旭等[18]基于Kirchhoff薄板理论与非局部弹性理论,对热环境中旋转功能梯度纳米环板的振动频率进行研究,通过微分求积法对径向和横向耦合运动变系数微分方程进行离散并求解.葛仁余等[19]通过应用微分求积法,将双材料平面接头问题转化为含应力奇性指数的常微分方程组的特征值求解问题,通过奇性指数的计算以确保工作条件下连接件在连接点处的强度足够.

本文以末端附加质量块的矩形等截面均质悬臂细长L梁为研究对象,根据所建立的动力学方程以及边界条件,用微分求积法对其固有振动特性进行了研究.首先通过对比研究,验证了本文所用的微分求积法计算过程与结果的正确性,并研究了末端质量、内外梁的长度比、宽度、厚度对各阶固有频率的影响.特别地,本文创新地运用微分求积这一方法求解悬臂L梁的固有振动特性,相比于传统的直梁结构,额外考虑了其内梁的扭转变形与拐点处特殊的连续性条件,从而确保了计算精度,推广了该方法在工程结构中的适用范围.此外,本文创新地将边界条件精确施加于边界点上,在进一步提高计算精度的同时简化了计算.

1 模型与动力学方程的建立

末端附加质量块的矩形等截面均质悬臂L梁模型如图1所示,L梁在计算过程中被分为内、外两段,以内梁末端(固支端)为原点建立正交固定坐标系O1X1Y1Z1,并以内、外梁连接拐点处为原点建立正交运动坐标系O2X2Y2Z2.

本文考虑内、外梁在振动过程中发生的XOZ面内的横向弯曲振动与内梁发生的扭转振动,由此引入内梁挠度w1、外梁挠度w2和内梁扭转角θ.令内、外梁均为满足跨高比大于10的细长梁,故可将两段梁均视为Euler-Bernoulli梁,忽略其剪切变形及绕中性轴转动惯量的影响.此时动力学方程为内梁的XOZ面内横向弯曲振动方程(1a)、扭转振动方程(1b)与外梁的XOZ面内横向弯曲振动方程(2):

(1a)

(1b)

(2)

其中EI为L梁的抗弯刚度,GIp为L梁的抗扭刚度,ρ为梁的密度,S为梁的横截面面积.

2 微分求积法求解

2.1 节点坐标的选取

分别将内、外梁的长度正规化为[0,1]后,取Chebyshev多项式的根作为节点坐标进行划分.在内、外梁各自的长度方向上分别划分N1与N2个节点,此时各节点坐标为

(3a)

(3b)

其中l1,l2分别为内、外梁的长度.

2.2 插值基函数的选取

选用Lagrange插值基函数进行离散,由插值理论可得

(4a)

(4b)

其中p1j(X),p2j(X)选用Lagrange插值基函数:

(5a)

(5b)

2.3 权系数矩阵的计算

将式(4a)两侧对X1求m阶导数,式(4b)两侧对X2求m阶导数,分别代入X1=x1i和X2=x2i并化为矩阵形式可得

(6a)

(6b)

其中内、外梁权系数矩阵中的每个元素分别为

(7a)

(7b)

将式(5)代入式(7),可得到一阶权系数表达式(8a)与高阶权系数表达式(8b):

(8a)

i,j=1,2,…,N1,2;i≠j;m=2,3,…,N1,2-1.

(8b)

2.4 边界条件的处理

在传统的节点替代法(δ法)的基础上,将施加于内部点的边界条件全部改为施加于边界点,并减少靠近边界点处相应数量内部点的四阶微分控制方程,得到改进后的边界条件:

固支端X1=0处

w1(0,t)=0,w′1(0,t)=0,θ(0,t)=0;

(9)

自由端X2=l2处

(10)

其中M2为外梁截面弯矩,Fs2为外梁截面剪力.

L梁拐点处的连续性边界条件可表示为

(11)

其中M1为内梁截面弯矩,T1为内梁截面扭矩,Fs1为内梁截面剪力.

将X1=x1i代入式(1a)、(1b),得到内梁的内部节点控制方程:

(12a)

(12b)

将X2=x2i代入式(2),得到外梁的内部节点控制方程:

(13)

由以上改进的节点替代法得到边界条件方程(9)、(10)、(11)共10个,内部节点控制方程(12)、(13)共2N1+N2-10个.

2.5 固有振动特性的求解

设w1(X1,t),w2(X2,t),θ(X1,t)的位移形式为

w1(X1,t)=φ1(X1)e-iωt,w2(X2,t)=φ2(X2)e-iωt,θ(X1,t)=φ(X1)e-iωt.

(14)

联立式(9)—(13),并将式(14)中的位移形式代入得

(15)

利用微分求积法将高阶微分方程组(15)转化为代数方程组:

(16)

上式可化简为如下矩阵形式:

(K-ω2M)α=0,

(17)

其中

α=[φ1(x11),φ1(x12),…,φ1(x1N1),φ2(x21),φ2(x22),…,φ2(x2N2),

φ(x11),φ(x12),…,φ(x1N1)]T.

3 结果对比验证

为了验证计算结果的正确性, 将本文结果与Cao等[20]利用Galerkin法得到的该系统的各阶固有频率进行对比.对比所用的材料与几何参数值如表1所示, 表2为微分求积法收敛性研究, 本文理论计算结果与Cao等[20]的理论计算结果以及PATRAN、COMSOL有限元结果的对比情况见表3.

表1 悬臂L梁的几何与材料参数表

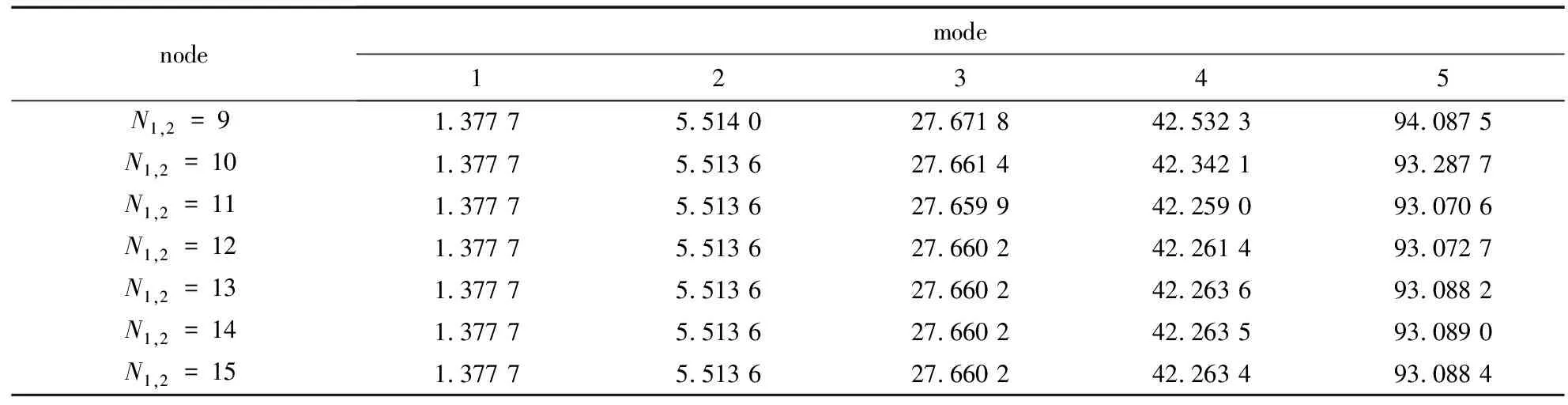
表2 不同节点数下的结构前五阶固有频率表(单位: Hz)

表3 结构前五阶固有频率对比表(单位: Hz)

如表2所示,当N1,2=13时,结构前五阶固有频率已经收敛,故随后的计算中取节点数N1,2=13.表3中对比结果显示,本文通过微分求积理论计算得到的各阶固有频率误差均不超过2%,故本文提出的用微分求积法求解悬臂L梁固有频率的方法是可行的.有限元求解得到结构前五阶模态如图2所示.

(a)一阶,1.405 3 Hz (b)二阶,5.554 0 Hz (c)三阶,27.779 0 Hz

4 参数讨论与分析

首先通过改变外梁长度l2调节内、外梁的长度比,其中当l2/l1为0时,悬臂L梁退化为悬臂直梁.如图3所示,随着长度比的增加,结构各阶固有频率均下降,且下降幅度逐渐减小.

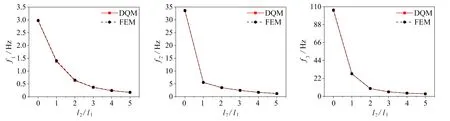
(a)一阶 (b)二阶 (c)三阶

图4为梁的宽度b的增加对系统固有频率的影响.由图可见微分求积法求得的各阶固有频率均呈现上升趋势,且上升幅度逐渐减小.

(a)一阶 (b)二阶 (c)三阶

如图5所示,随着梁厚h的增加,结构各阶横向弯扭振动固有频率均显著上升,在本文研究范围内,这一变化趋势接近线性.

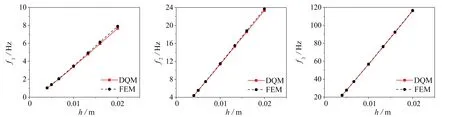
(a)一阶 (b)二阶 (c)三阶

图6为梁的末端质量m的增加对系统固有频率的影响,由图可知各阶固有频率均呈现下降趋势,且下降幅度逐渐减小.

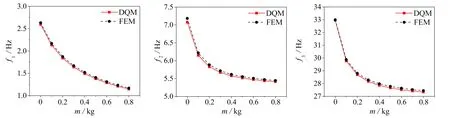
(a)一阶 (b)二阶 (c)三阶

综上所述,通过增大梁长比l2/l1、末端质量m,或减小梁宽b、梁厚h等方式均可实现固有频率的降低.在本文研究范围内,利用微分求积法求解得到的前五阶固有频率与COMSOL有限元结果的对比误差均不超过5%,故该算法具有高阶精度.值得注意的是,造成这一误差的主要原因在于:梁结构参数的某些改变导致该结构与Euler-Bernoulli梁理论适应性降低,因此为保证各阶固有频率的计算精度,末端质量m和梁宽b均不宜取值过大,梁长l1,l2也不宜取值过小,应满足l1,2≥10b.

5 结 论

本文利用微分求积法,对末端附加质量块的矩形等截面均质悬臂细长L梁的各阶固有频率与模态进行了计算.首先在内、外梁末端分别建立正交坐标系后,建立了结构的动力学方程.之后运用微分求积法,将内、外梁长度方向上的计算区间正规化为[0,1],选取Chebyshev多项式的根作为节点坐标划分计算区域,并选用Lagrange插值基函数进行插值,进一步求得各阶权系数.在列出直接法或改进后的节点替代法处理后的边界条件方程与连续性条件方程以及内、外梁的内部节点控制方程后,可将方程中给定节点处的函数与其各阶导数项用求解域内全部节点函数值的加权和进行表示,整理得到代数方程组并表示为矩阵形式,通过求解广义特征值问题得到结构各阶固有频率与模态.最后研究了末端质量、内外梁的长度比、宽度、厚度对结构各阶固有振动特性的影响.本方法可以进一步应用推广到相关结构振动的研究中.