乙醇液滴撞击高温壁面蒸发过程的模拟预测研究*

马小晶, 周 鑫, 吐松江·卡日, 许瀚文

(新疆大学 电气工程学院, 乌鲁木齐 830047)

0 引 言

液滴撞击高温壁面后的蒸发现象普遍存在于自然界和工业生产中[1].液滴撞击高温壁面后,由于相变作用内部产生大量气泡,气泡破碎产生二次液滴,液滴表面产生不规则形变.显然,液滴撞击蒸发过程是一个伴随着能量交换和相变过程的复杂传热传质问题.

目前,国内外学者已采用多种研究方法,对液滴撞壁这一复杂的流动过程展开了大量研究.沈胜强等[2]通过高速摄像仪观测了水和乙醇两种液滴撞击高温壁面的流动及蒸发过程,分析讨论了液滴的蒸发特性.Guo等[3]通过实验研究了液滴冲击高温圆柱表面的流动传热问题,探讨了柱面温度等因素对液滴沸腾流动过程的影响.He等[4]通过粒子图像测速法研究了不同体积比乙醇水溶液液滴蒸发过程,并分析了液滴蒸发机理.Susmita等[5]通过实验方法研究了水滴在光滑疏水表面的蒸发特性,观察研究了液滴几何参数随时间的变化.

近几年以来,数值模拟方法已经广泛应用于多相流动和传热等领域,并且取得了大量研究成果[6].吴苏晨等[7]基于格子Boltzmann方法建立了数值模型,研究了液滴撞击过程中的相变传热机制,并分析讨论了壁面温度和Weber数(We)的影响规律;董佰扬等[8]基于分段模拟蒸发的数值模型,通过引入动态接触角实现了恒接触半径蒸发模式到恒接触角蒸发模式的连续模拟;Semenov等[9]结合蒸发扩散模型和动力学模型,研究了蒸发潜热等因素对静置在高导热基底上不同大小液滴蒸发速率的影响.

目前,学者对液滴撞击高温壁面后液滴沸腾蒸发过程中剩余液滴随时间的变化过程研究还较少,因此本文采用CLSVOF(coupled level set and volume of fluid)方法,基于Lee模型建立液滴撞击高温壁面沸腾蒸发模型,模拟研究了乙醇液滴撞击高温壁面后的沸腾蒸发过程,分析总结了液滴蒸发剩余量随时间的变化规律,并通过与相关实验结果进行对比,验证了模型的有效性.在此基础上,模拟分析了壁面润湿性和撞击速度等对乙醇液滴沸腾蒸发过程的影响.鉴于模拟液滴沸腾蒸发过程中存在计算量大和时间消耗长的问题,本文在模拟研究的基础上,通过引入机器学习算法,对乙醇液滴蒸发剩余量随时间的变化规律进行了预测研究.

1 计算模型和模型验证

1.1 控制方程

本文基于CLSVOF方法建立数值模型,将乙醇和乙醇蒸汽均视作不可压缩流体,控制方程包括连续性方程、动量守恒方程和能量守恒方程[10],即

∇·u=0,

(1)

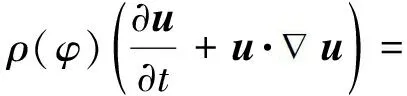
(2)

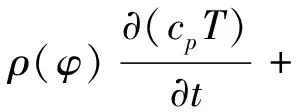
(3)

式中,u为速度,m·s-1;T为温度,K;P为压强,Pa;μ为动力黏度系数,N·s·m-2;ρ为密度,kg·m-3;σ为表面张力系数,N·m-1;κ为界面曲率,m-1;cp为定压比热容,J·(kg·K)-1;λ为导热系数,W·(m·K)-1;δ(·)为Dirac函数;φ为距离函数.为了在相界面处实现流体之间密度和黏度参数的光滑过渡,在计算流体密度ρ(φ)和黏度μ(φ)时,引入了Heaviside函数,其定义为

(4)

式中,h为相界面过渡区域宽度的一半,本文取为1倍的网格单元宽度.黏度μ(φ)和密度ρ(φ)为

μ(φ)=μl(1-H(φ))+μgH(φ),

(5)

ρ(φ)=ρl(1-H(φ))+ρgH(φ).

(6)

在运算过程中,每次循环计算均需要结合VOF相函数α和level set距离函数φ重新构造气液两相的界面,并对level set距离函数φ初始化.CLSVOF方法通过求解VOF相函数α和level set距离函数φ的对流输运方程,精准捕捉两相流界面.

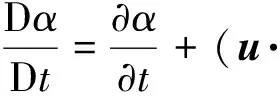
(7)

(8)

通过level set距离函数φ可得界面法向量n和界面曲率κ,即

n=∇φ/|∇φ|,

(9)

κ=∇·(∇φ/|∇φ|).

(10)

考虑到壁面黏附作用,通过接触角调整壁面附近单元的表面法向量ns为

ns=nwcosθ+τwsinθ,

(11)

式中,nw和τw分别为壁面单位法向量和切向量;θ为接触角.

重新对距离函数φ初始化,函数φ的值是计算单元中心到相界面的最小距离,函数φ的符号可以由VOF相函数α来确定,即

Sφ=sgn(0.5-α),

(12)

式中,sgn(·)是符号函数.

1.2 Lee模型

乙醇液滴撞击高温壁面后,由于固液传热作用,液滴在达到饱和温度后产生沸腾蒸发现象,本文采用应用较广的Lee模型[11]模拟液滴相变过程.在Lee模型中,质量转移由蒸汽和液体相间的输运方程控制决定,即

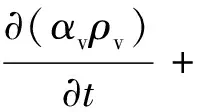
(13)

(14)

(15)

式中,ml和mg分别为液相和气相的相变质量转移速率,即蒸发速率;Tc为控制单元温度,Ts为饱和温度;γ为相变调节系数.Lee模型通过汽化潜热r和质量转移速率ml来计算蒸发过程向外散发的热量,即在单位时间内蒸发散热Qv等于液滴的汽化潜热r和质量转移速率ml的乘积:

Qv=mlr.

(16)

1.3 动态接触角模型

由式(11)可知,接触角会通过壁面黏附作用影响液滴流动过程,同时接触角又会随流动过程发生改变,采用静态接触角求解会导致模拟结果出现较大偏差[12].因此,本文引入Kistler经验公式计算动态接触角[13],即根据静态接触角θe,可得动态接触角θd为

θd=F(Ca+F-1(θe)),

(17)

(18)

式中,Ca为毛细数.

1.4 模型的验证

模拟研究可以将物理模型简化为二维平面模型[10],初始液滴视为球形.初始时刻液滴底部与壁面相切,此时液滴的初始速度u0可视为液滴的撞击速度uc,即uc=u0.压力与速度耦合采用PISO方法,求解压力采用PRESTO方法,对level set方程求解采用QUICK格式,动量和能量方程求解采用二阶迎风格式.模拟过程中,通过相函数α来计算乙醇液滴的蒸发剩余量Sv,并进行无量纲处理,即

(19)

式中,s为一个计算网格的大小,a和b分别为计算域内沿坐标方向上的网格数量,S0为液滴初始量,计算过程液滴的体积分数为1.

为了验证二维模型网格无关性,计算域取1 cm×2 cm的长方形区域,分别采用80×160,100×200,125×250和160×320的四边形结构化网格模拟乙醇液滴撞击高温亲水壁面的蒸发过程,图1为4种网格密度下乙醇液滴蒸发剩余量Sv随时间的变化曲线.由图1可看出,当网格密度达到125×250时,继续增加网格密度对计算结果的影响可近似忽略,即计算结果不再与网格密度有关.因此,后续研究均采用125×250的结构化网格.

图1 不同网格密度下蒸发剩余量Sv随时间的变化曲线

为了验证乙醇液滴蒸发模型的有效性,本文将模拟结果与文献[14]中乙醇液滴撞击高温壁面汽化过程的实验结果进行了对比,如图2所示.模型中乙醇液滴的物性参数与尺寸均与实验一致,密度ρ=800 kg·m-3,表面张力系数σ=0.022 8 N·m-3,动力黏度μ=0.001 001 Pa·s,计算动态接触角时,取θe=40°.乙醇液滴初始温度Td=293 K,乙醇液滴饱和温度Ts=351 K,撞击速度uc=0.23 m·s-1,直径d0=1.64 mm.

(a)Tw=400 K

从图2中可以看出,模拟研究中乙醇液滴撞击高温壁面的沸腾蒸发过程与实验基本一致.在撞击初期,乙醇液滴在惯性力的作用下逐渐铺展,此时乙醇液滴还未达到饱和温度,沸腾蒸发现象不明显.由于壁面与液滴之间的固液传热作用,乙醇液滴温度逐渐升高,在达到液滴饱和温度后开始沸腾,发生剧烈汽化作用,液滴底部产生大量气泡,气泡破碎后产生大量二次液滴,液滴表面产生不规则形变.

图2(a)中壁面温度Tw=400 K,图2(b)中壁面温度Tw=420 K,从图中可看出,随着壁面温度升高,乙醇液滴沸腾更加剧烈,沸腾蒸发过程明显加快.图3为乙醇液滴撞击高温壁面后液滴蒸发剩余量Sv随时间的变化关系.从图3可以看出,在液滴撞击初始阶段,乙醇液滴的温度较低,液滴蒸发剩余量随时间的变化相对平缓.由于壁面与液滴之间的传热作用,乙醇液滴的温度逐渐升高,液滴达到饱和温度后开始沸腾,蒸发速度加快,液滴蒸发剩余量随时间的变化加快.乙醇液滴撞击400 K高温壁面时,液滴蒸发过程持续695 ms,撞击420 K高温壁面时,液滴蒸发过程持续455.1 ms.

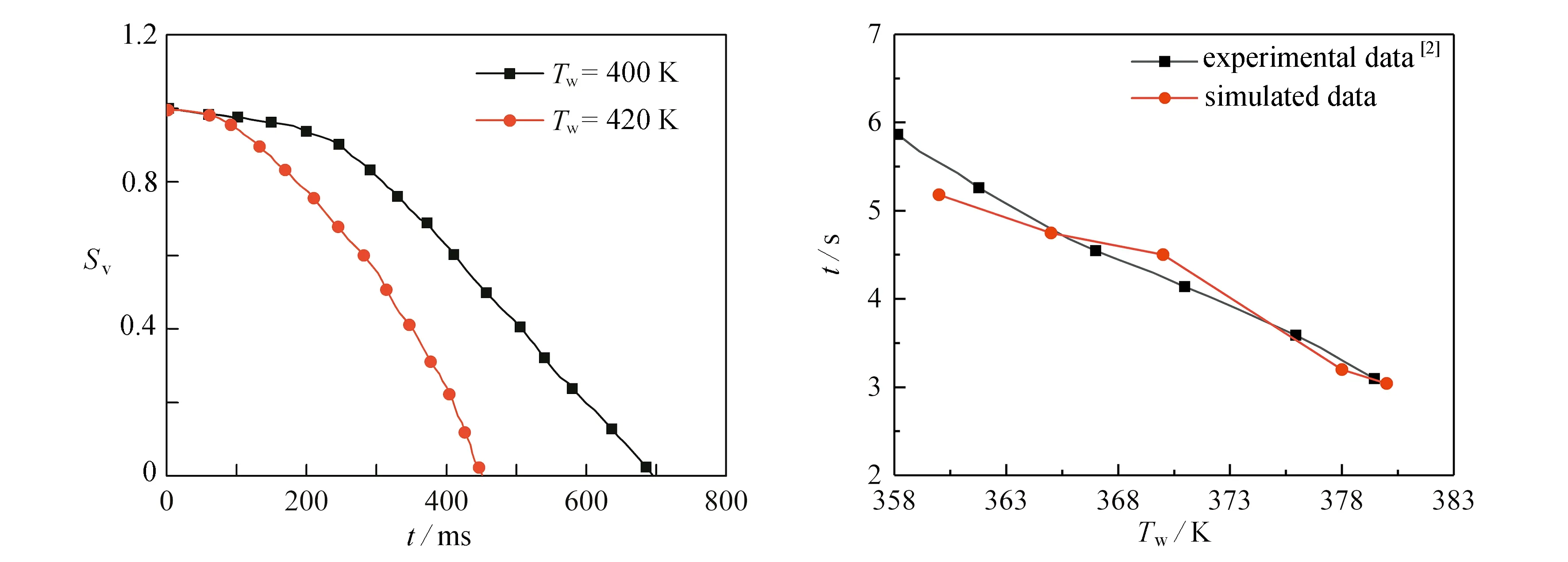
图3 乙醇液滴撞击不同温度壁面Sv随时间的变化曲线 图4 乙醇液滴撞击不同温度壁面蒸发时间对比

为了进一步验证液滴蒸发模型的可行性,本文分别模拟了多种壁面温度下乙醇液滴沸腾蒸发过程,并将模拟结果与沈胜强等[2]的实验结果进行对比,图4为实验数据和模拟数据的对比.由图4中可以看出,在Tw=360 K时误差最大,在其他壁面温度下,模拟液滴蒸发时间与实验数据误差很小.表1给出了乙醇液滴撞击不同温度壁面后蒸发时间与实验结果[2]的误差对比.从表中模拟结果与实验结果的对比中可以看出,在Tw=360 K时误差最大,约为-6.98%.在其他壁面温度下,模拟乙醇液滴蒸发时间与实验数据误差较小,印证了模拟结果准确可靠.

表1 乙醇液滴完全蒸发时间与实验结果误差对比

2 数值模拟结果与分析

2.1 液滴撞击速度对蒸发过程的影响

为了研究撞击速度对乙醇液滴撞击高温壁面沸腾蒸发过程的影响,本文分别模拟研究了直径为1.64 mm的乙醇液滴以不同初速度撞击高温壁面后的沸腾蒸发过程.在计算过程中,取Tw=400 K,计算动态接触角时,取θe=40°.图5给出了乙醇液滴以不同速度撞击高温壁面后蒸发剩余量Sv随时间的变化曲线.

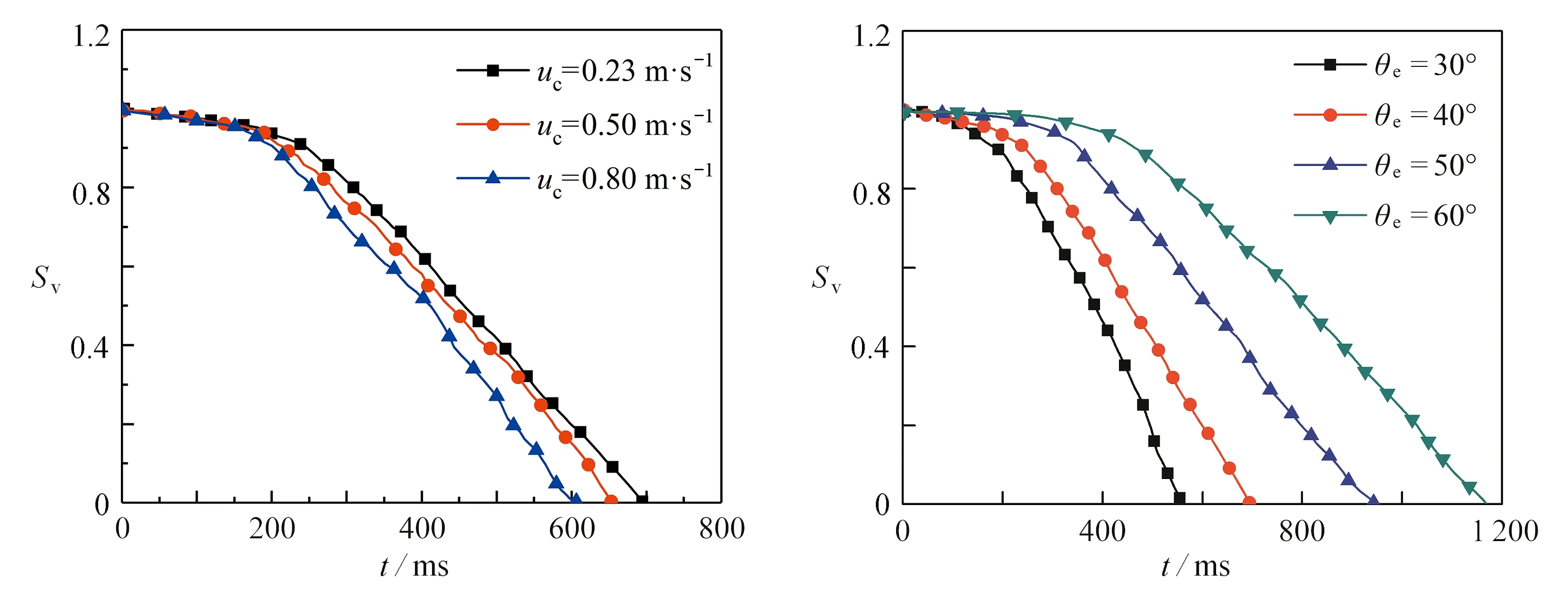
图5 液滴以不同速度撞击高温壁面后Sv随时间的变化曲线 图6 乙醇液滴撞击不同润湿性壁面Sv随时间的变化曲线

由图5可知,乙醇液滴以不同速度撞击高温壁面后,液滴蒸发剩余量Sv随时间的变化规律基本一致.在撞击初期,乙醇液滴还未达到饱和温度,沸腾蒸发过程不明显,Sv随时间变化较小.随着壁面与液滴之间的温差传热作用,乙醇液滴温度逐渐升高,在达到饱和温度后开始沸腾蒸发,液滴蒸发剩余量Sv迅速减少,直至液滴完全汽化.由图5中可以看出uc越大时,tmax越小,这是由于uc越大,乙醇液滴在撞击后越易铺展,液滴与壁面的接触面积越大,液滴温度上升越快,达到饱和温度所需的时间也越短,液滴越早进入沸腾蒸发阶段.在随后的沸腾蒸发阶段,液滴吸收热量与蒸发散热保持平衡,液滴的蒸发速率没有发生明显变化,液滴蒸发曲线斜率基本保持不变,且液滴不同撞击速度的蒸发曲线斜率也没有明显差异.液滴撞击速度对沸腾蒸发过程的影响主要是影响液滴与壁面的接触面积.

2.2 壁面润湿性对蒸发过程的影响

现有研究表明壁面润湿性是影响液滴沸腾蒸发过程的重要影响因素之一[15-16].本文模拟了直径1.64 mm的乙醇液滴撞击不同润湿性高温壁面后的沸腾蒸发过程.Tw=400 K,Td=293 K,uc=0.23 m·s-1,图6给出了乙醇液滴撞击不同润湿性高温壁面后Sv随时间的变化曲线.

由图6可知,乙醇液滴撞击不同润湿性壁面后,液滴的沸腾蒸发过程存在较大差异.壁面接触角越小,壁面的亲水性越好,液滴撞击壁面后,易于铺展,即液滴与壁面的接触面积较大,由于高温壁面和液滴的传热作用,液滴的温度上升快.液滴达到饱和温度所需的时间越短,撞击后发生沸腾蒸发的时间点越早.同理,在撞击铺展后期,液滴在表面张力等作用下会逐渐收缩,壁面接触角越大,其疏水性越强,液滴越易于收缩,即铺展面积较小,因此,液滴蒸发相变速率有所减慢,Sv随时间的变化曲线相对平缓.

3 预测研究与分析

3.1 液滴撞击高温壁面蒸发过程预测研究

近些年来,随着人工智能的快速发展,机器学习作为人工智能领域内的一门重要学科,已经得到了广泛的应用[17].本文通过不同机器学习算法建立预测模型,对乙醇液滴撞击高温壁面后蒸发剩余量Sv随时间的变化进行了预测研究,并通过对比预测结果与模拟结果,选出最优预测模型.

本文选取壁面温度,表征壁面润湿性的接触角,液滴撞击速度以及撞击时间作为特征参数,液滴蒸发剩余量Sv为目标参数,液滴初始温度293 K,环境温度298 K.本文通过收集14种工况下的12 600组模拟数据建立数据集,并按4∶1的比例将数据集划分为训练集和测试集.此外,单独模拟一种工况下的乙醇液滴撞击蒸发过程并收集Sv随时间的变化数据作为结果验证.相关参数如表2所示.

表2 模拟工况相关参数

图7为采用不同机器学习算法的预测结果与模拟结果的对比.从图7中可以看出,针对同一数据集,不同机器学习算法的预测结果存在差异.在本算例中,K最近邻(K-nearest neighbor, KNN)算法和神经网络(multilayer perceptron, MLP)算法的预测曲线与模拟曲线更加接近,预测结果明显优于采用支持向量(support vector regression, SVR)算法和随机森林(random forest, RF)算法所得的预测结果.

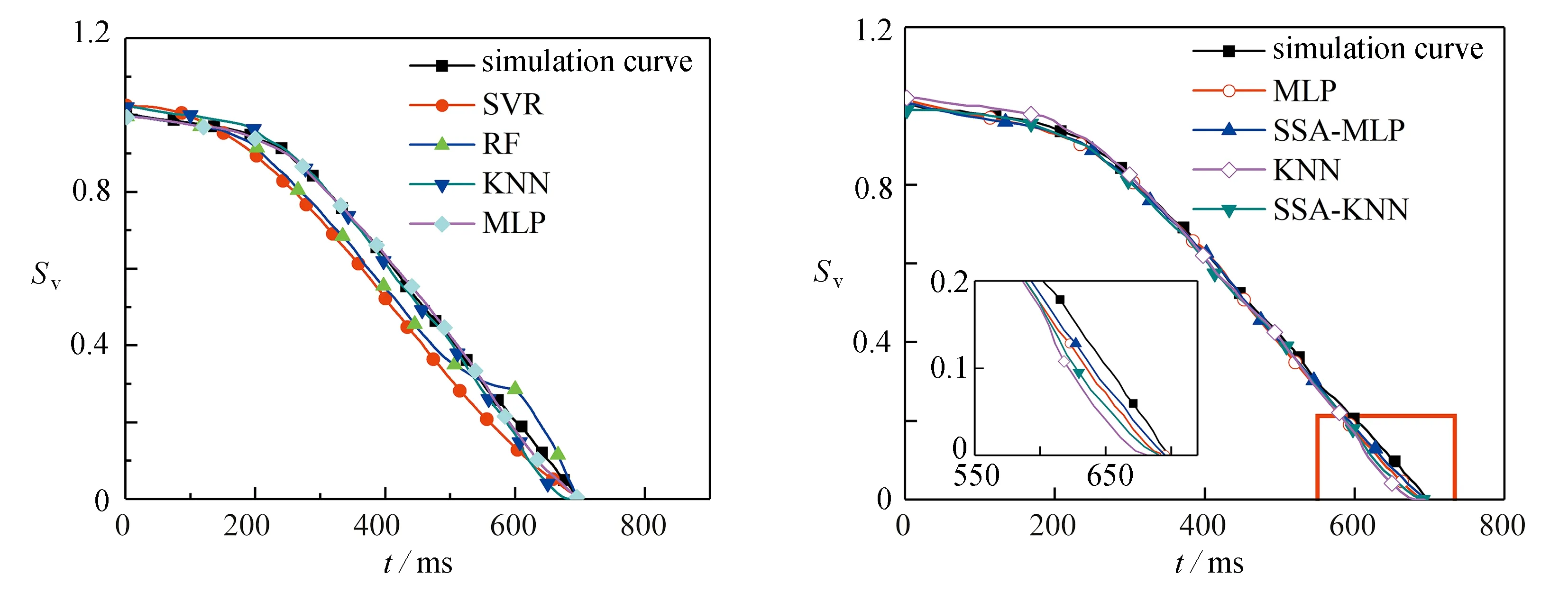
图7 不同机器学习算法的预测结果与模拟结果的对比 图8 SSA优化预测曲线

表3给出了4种算法的预测结果与模拟结果的误差对比.由表3可知,基于 MLP算法建立预测模型的预测结果与模拟结果的误差最小,且决定系数R2最接近1,这说明通过MLP算法获得的预测曲线与模拟曲线拟合程度最好,预测结果最精确.

表3 预测结果与模拟结果的误差对比

3.2 超参数优化

为了进一步提高预测精度,本文引入麻雀搜索算法(sparrow search algorithm, SSA)将预测模型输出的均方误差作为优化算法目标参数,分别对KNN模型和MLP模型超参数进行大范围搜索,能够快速准确地在张量空间中找到 KNN模型和MLP模型的最优超参数.经过SSA优化后预测曲线如图8所示.观察图8可知,采用SSA优化后,预测曲线更加接近模拟曲线.

表4给出了优化后预测结果与模拟结果的误差对比.对比表3和表4可知,引入SSA对KNN模型和MLP模型超参数进行优化后,两种预测模型的预测误差均有所减小,决定系数R2比优化前更接近1,预测曲线与模拟曲线的拟合程度更高,预测精度更高.采用SSA优化预测模型的超参数能够有效提高预测模型的预测精度.

表4 采用SSA优化后预测结果与模拟结果误差对比

4 结 论

本文研究采用CLSVOF方法,引入动态接触角计算模型,建立了乙醇液滴撞击沸腾蒸发数值模型,对乙醇液滴撞击后的沸腾蒸发过程展开研究,通过与实验结果的对比验证了所建模型的有效性.在此基础上,通过机器学习算法,建立了预测模型,对乙醇液滴撞击高温壁面后Sv随时间的变化进行了预测研究,得出了以下结论:

1)乙醇液滴撞击高温壁面后在惯性力的作用下逐渐铺展,由于壁面与液滴之间的传热作用,液滴温度逐渐升高,在达到液滴饱和温度后进入沸腾蒸发阶段,液滴从底部开始产生大量气泡,气泡破碎,在相界面接触线处产生二次液滴,液滴表面产生不规则形变.

2)在乙醇液滴撞击初始阶段,由于液滴的温度较低,Sv随时间的变化相对平缓;当液滴达到饱和温度后进入沸腾蒸发阶段,蒸发速度加快,Sv随时间的变化加快.在相同撞击条件下,壁面温度越高,固液传热作用越强,液滴进入沸腾蒸发阶段所需时间越短,液滴蒸发速度越快.在壁面温度相同的条件下,液滴与壁面的接触角越小、液滴撞击速度越快,液滴越易铺展,液滴撞击后与壁面的接触面积越大,液滴更早进入沸腾蒸发阶段.液滴在进入沸腾蒸发阶段后,液滴吸收热量与蒸发散热保持平衡,液滴的蒸发速率没有发生明显变化.

3)采用4种机器学习算法建立预测模型,对乙醇液滴撞击高温壁面后Sv随时间的变化进行了预测研究,并将预测结果与模拟结果进行对比.采用MLP算法得到的预测曲线与模拟曲线更加接近,误差更小,MLP算法更适合用于预测研究乙醇液滴撞击高温壁面后的沸腾蒸发过程.在此基础上,采用SSA对预测模型进行了优化,提高了预测模型的精度.