SAV/重心插值配点法求解Allen-Cahn方程*

黄 蓉, 邓杨芳, 翁智峰

(华侨大学 数学科学学院, 福建 泉州 362021)

0 引 言

Allen-Cahn方程是一类求解界面问题的数学模型,最早由Allen和Cahn[1]在1979年引入,用来描述晶体反相位边界的运动.此后,Allen-Cahn方程在描述各类复杂现象中占据着重要地位,如图像处理[2]、晶体生长[3]、平均曲率-流量[4]等.本文考虑如下的Allen-Cahn方程:

(1)

式中,u(x,t)是相场函数,F(u)=(u2-1)2/(4ε2),ε>0是界面宽度参数,Ω∈2是有界区域.

Allen-Cahn方程可以视为自由能泛函的L2梯度流[5]:

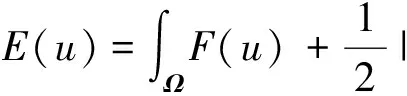
(2)

将能量泛函E(u)关于t求导,可知Allen-Cahn方程满足能量递减规律,即

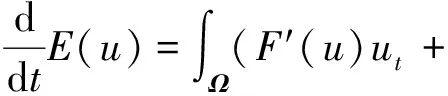
(3)

Allen-Cahn方程具有广泛的应用前景,但其解析解往往难以求出,因此许多学者致力于其数值模拟的研究,提出了各种稳定高效的数值模拟方法.Zhai等[6]采用紧致差分交替方向隐式(ADI)方法求解高维Allen-Cahn方程;Weng等[7]基于算子分裂法求解Allen-Cahn 方程,并给出了格式的稳定性分析;Li 等[8]采用有限元法建立Allen-Cahn方程的无条件能量稳定格式,并对数值格式进行了误差分析;Liao等在文献[9]中构建了变步长的二阶向后差分格式(BDF2)来求解Allen-Cahn方程; Li和Song等[10]采用非线性内罚间断Galerkin有限元(IPDGFE)方法求解Allen-Cahn方程,建立了时间二阶精度、能量稳定的高效数值格式; Li和Ju等[11]提出了守恒型Allen-Cahn方程的极大值原理分析;汪精英等[12]基于Laplace变换,结合谱方法和有限差分法求解了分数阶Cahn-Hilliard相场方程.

目前,无网格方法[13-14]逐渐引起学者们的关注,重心Lagrange插值配点法是一种新型的无网格方法,由Lagrange插值公式引入重心权推导而来,可以克服后者数值不稳定的缺陷.当节点数量增多时,采用Lagrange插值公式来逼近函数时易出现Runge现象,节点适应性差;而重心Lagrange插值公式在选取特殊的节点时,如Chebyshev点族,具有优良的数值稳定性,解决了Lagrange插值公式逼近函数时出现的震荡现象,提高了节点的适应性.此外,重心Lagrange插值配点法兼具精度高、编程简单、易于计算等优势.近年来,重心Lagrange插值配点法已被应用于求解各类问题,如平面弹性问题[15]、Burgers方程[16]、最优控制问题[17]、Allen-Cahn方程[18]、高维Fredholm积分方程[19]等.尽管关于重心Lagrange插值配点法数值应用的研究很多,但目前该方法的收敛性分析、误差分析的理论工作还较少.最近,Yi 等[20]提出了求解时间分数阶电报方程的重心Lagrange插值方法,并给出了离散系统的误差分析.

近年来提出的标量辅助变量(SAV)方法[21-25]是一种新型高效的处理非线性问题的策略.该方法基于IEQ格式改进,保留了IEQ 格式的优势并克服其缺陷,为梯度流模型构建时间离散化方案提供了一种高效而稳定的策略.SAV方法具备两大优势:一方面,SAV格式扩大了IEQ格式的使用范围,不再局限于非线性势函数有下界的情形下使用;另一方面,SAV方法借助引入不依赖空间变量的辅助变量,在时间步只涉及到常系数,构建线性无条件能量稳定的离散系统.目前,SAV方法已被应用于求解各种问题.Huang等[22]为梯度流模型提出了一种高效且准确的新型SAV方法.Cheng等[23]提出了广义SAV(G-SAV)方法,该方法可保持原始能量而非修改能量的无条件能量稳定,同时也能保持原始SAV方法的基本优势.Li和Shen[24]基于SAV Fourier谱格式求解相场晶体方程,并给出了无条件能量稳定格式的误差分析.

基于前人的工作,本文着重于空间离散,采用新型的重心插值配点格式来构建二维Allen-Cahn方程的SAV无条件能量稳定数值格式.在时间方向上采用的离散方法是Crank-Nicolson(CN2)和BDF2.此外,给出了重心Lagrange插值配点格式的逼近性质.为验证所提格式的高精度,将重心插值配点格式与有限差分格式进行对比,数值算例验证了基于SAV方法的重心Lagrange配点格式具有指数收敛的特性.

1 重心Lagrange插值配点法

本文采用一种新型的无网格方法——重心Lagrange插值配点法,对空间方向进行离散.对于M+1个互异节点xk(k=0,1,…,M),令函数V(x)在节点xk处的函数值是Vk,插值多项式P(x)在离散节点xk处成立P(xk)=Vk.

将多项式P(x)改写成Lagrange插值形式:

(4)

式中, Lagrange插值基函数为

记L(x)=(x-x0)(x-x1)…(x-xM),则基函数Lk(x)的另一表达式为

(5)

将式(5)代入式(4),并令P(x)=1,可得

(6)

据上式,可推出重心Lagrange插值公式为

(7)

令P(x)关于x求导,并在离散节点xi处成立,即

(8)

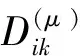
(9)

重心插值配点法在选取Chebyshev点族时具有优良的数值稳定性,本文选取的节点和对应的重心权表达式为

(10)

(11)

针对选取的第二类Chebyshev点族,令空间x,y方向的节点数分别为M,N.类似上述推导过程,则二元函数u(x,y)在张量型节点(xk,yj)的重心Lagrange插值公式为

(12)

考虑u(x,y)分别对变量x,y求二阶偏导数,即

(13)

2 Allen-Cahn方程的SAV配点格式

2.1 Allen-Cahn方程的离散格式推导

在本小节中,构造二维Allen-Cahn方程的全离散格式.应用SAV策略,在时间方向采用CN2格式离散,空间方向采用重心Lagrange插值配点格式离散,建立时间二阶精度的SAV数值格式,记为CN2-BLI.为便于分析,定义(·,·)和‖·‖分别表示L2内积和L2范数.

为构建SAV方案,在Allen-Cahn方程中引入变量ω,将式(1)改写为

ω=-Δu+F′(u).

(14)

(15a)

(15b)

(15c)

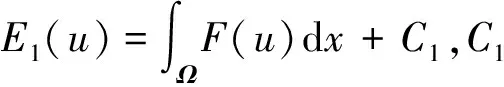
分别将式(15a)内积ω、式(15b)内积∂u/∂t、式(15c)乘以2R,可得

(16)

式(16)表明修正能量E(u)=(u,-Δu)/2+R2是无条件能量稳定的.

在时间方向采用CN2格式进行离散,则Allen-Cahn方程的半离散格式如下:

(17a)

(17b)

(17c)

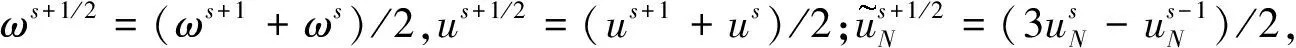
将式(17a)、式(17b)分别与ωs+1/2,us+1-us作内积,式(17c)乘以2rs+1/2,可得

(us+1-us,ωs+1/2)+τ(ωs+1/2,ωs+1/2)=0,

(18)

(19)

(20)

将式(18)—(20)结果化简,可得

(21)

整理如下:

(22)

综上,Allen-Cahn方程的半离散格式(17a)—(17c)是关于时间无条件能量稳定的.

(23)

式中,空间离散算子Dh=C(2)⊗IN+IM⊗D(2),C(2)和D(2)分别是空间x和y方向的二阶微分矩阵.

(24)

记A=I-(τ/2)Dh,上式方程两边同时乘以A-1,即

(25)

将式(25)与σs作内积,即

(26)

经整理,可得

(27)

故

(28)

(29)

类似地,若采用BDF2格式结合重心Lagrange配点法来离散Allen-Cahn方程,构造基于SAV方案的另一种二阶离散格式,记为BDF2-BLI,算法格式如下:

(30)

2.2 重心插值公式误差估计

基于插值逼近误差结论,分析重心Lagrange配点格式求解Allen-Cahn方程的相容性误差.

针对函数u(x,y),对应的重心Lagrange插值函数为uh(x,y),误差是η(x,y)=u(x,y)-uh(x,y).引用文献[20]定理内容,即有如下引理.

引理1 如果u(x,y)∈C(n+1)(Ω),Ω=[a,b]×[c,d]是具有Lipschitz连续边界的非空区域,则如下的误差估计结论成立:

(31)

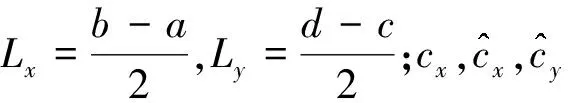
由引理1结论,设函数u(x,y,t)的重心Lagrange插值逼近函数为uh(x,y,t),则以下结论成立:

(32)

根据重心插值逼近的误差结果可知,该配点格式是在空间上具有指数收敛的特性,并且微分算子的阶数决定了算法求解方程的空间收敛阶.

3 数 值 实 验

在本节中,选取Dirichlet边界条件,给出4个数值算例来验证配点格式的有效性与高精度.针对二维Allen-Cahn方程,分别验证两种SAV配点格式均具有高精度,且满足无条件能量稳定特性;此外,分别采用重心插值配点法和五点差分法对空间方向离散,将数值结果对比分析.

3.1 算例1

为验证CN2-BLI、BDF2-BLI格式的时间收敛阶,且满足能量递减规律,选取真解如下:

u=cos(t)sin(πx)sin(πy).

(33)

令Ω=[-1,1]2×(0,T],ε=0.2,M=N=20,T=1,则两种数值格式求解Allen-Cahn方程的误差、收敛阶结果见表1.由表1可知:CN2-BLI、BDF2-BLI两种数值格式的时间收敛阶均为二阶;在选取相同的剖分节点时,CN2-BLI格式求解得到的L2误差小于BDF2-BLI格式的L2误差,表明前者的数值求解效果略优于后者.

表1 采用CN2-BLI、BDF2-BLI格式求解u的L2误差

基于SAV策略,分别选择不同的空间离散技术求解Allen-Cahn方程,即重心Lagrange插值配点法、五点差分法来离散,得到的L2误差结果见表2.由表2可知:CN2-BLI、BDF2-BLI格式在空间上采用重心Lagrange插值配点法离散,当选取节点M=N=15时,L2误差均可达到10-8量级;CN2-FD格式空间离散方式是五点差分法,在M=N=120时,误差仅达到10-4量级.通过对比误差结果可知,前两种格式在选取少量节点时即可达到高精度,即重心Lagrange插值配点法具有高精度的优势.

表2 不同空间离散方案的精度对比结果

对于上述剖分,验证不同数值格式求解Allen-Cahn方程时满足能量递减规律.

根据图1所示,令τ=0.001,0.000 1,两种SAV配点格式的能量耗散曲线均呈现下降趋势,表明应用SAV策略的重心Lagrange配点格式满足能量递减的性质.

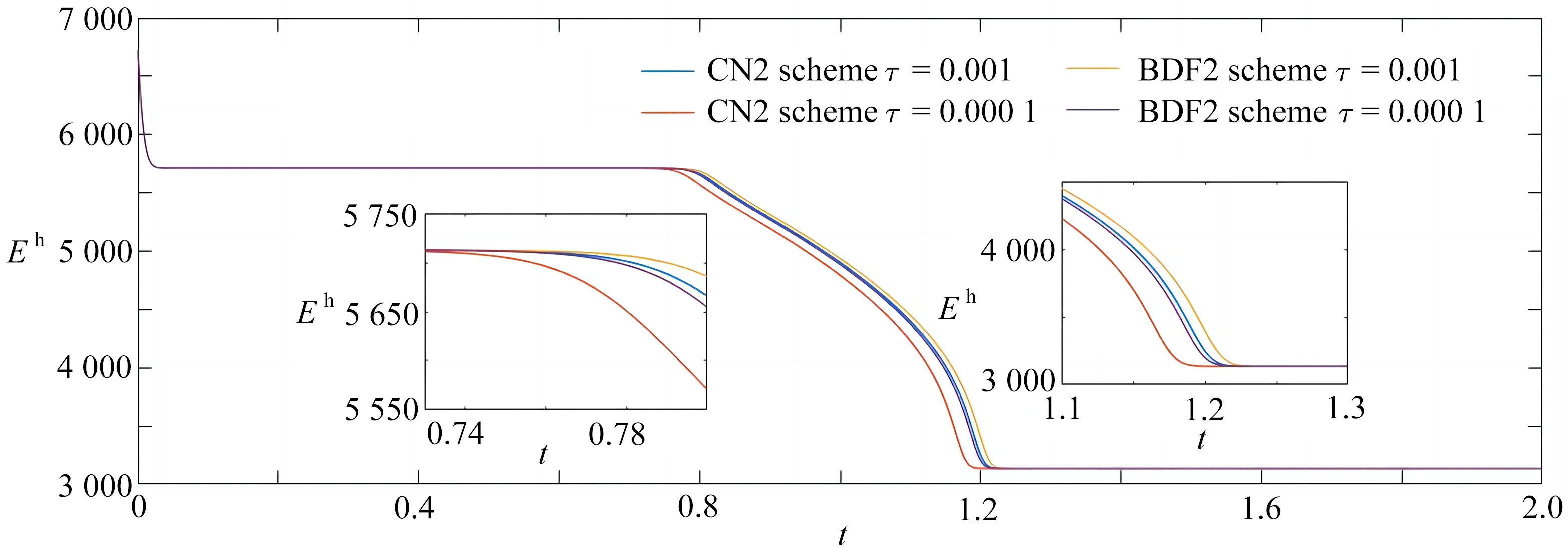
图1 不同数值格式的能量演化图(ε=0.1)

令参数ε=0.3,τ=0.001,T=1,选取不同的空间剖分节点数(M=N),则AC方程的空间收敛阶结果如图2所示.图2表明当空间采用重心Lagrange插值配点法离散时,CN2-BLI、BDF2-BLI格式在空间方向上均具有指数收敛的特性.

图2 不同数值格式的空间收敛阶

3.2 算例2

对于问题(1),令Ω=[-1,1]2×(0,1],给定初值如下:

u0(x,y)=(x2-1)(y2-1)sin(πx)sin(πy).

(34)

选取空间节点数M=N=40,设定参数ε=0.06,Δt=0.002,则数值解随时间的演化如图3所示.图3是在给定初值的条件下,数值解在t=0 s,0.2 s,0.7 s,1 s的演化情况.随着时间的累积,数值解随之出现变化层,然后达到亚稳态,最后达到稳态.

(a)t=0 s (b)t=0.2 s (c)t=0.7 s (d)t=1 s

3.3 算例3

针对Allen-Cahn方程, 考虑选取随机初值如下:

u0(x,y)=0.95rand(x,y)+0.05.

(35)

令区域为Ω=[-1,1]2×(0,1],选取参数ε=0.05,τ=0.000 1,M=N=40, 则u在不同时刻的数值解如图4所示.图4展示了在初值随机分布的情形下,SAV配点格式求解Allen-Cahn方程在t=0 s,0.03 s,0.08 s,0.5 s,1 s时的数值解快照,随着时间变化,相函数从分离状态逐渐达到聚合状态.

(a)t=0 s (b)t=0.03 s (c)t=0.08 s (d)t=0.5 s (e)t=1 s

3.4 算例4

在本算例中,研究数值解的粗化现象.给定参数ε=0.05,τ=0.002,T=0.2,初值如下:

u0(x,y)=h1(x,y)h2(x,y),

(36)

式中

(37)

(38)

令Ω=[-1,1]2×(0,T],空间剖分为M=N=60,则数值解在不同时刻的快照如图5所示.图5展示了相场函数u的数值解随着时间变化而逐渐融合的过程:初始时刻呈现“哑铃状”图像;在t=0.1 s演变成椭圆状;其后在t=0.15 s融合成小型圆点;最后呈现完全融合状态.

(a)t=0 s (b)t=0.05 s (c)t=0.1 s (d)t=0.15 s (e)t=0.2 s

4 结 束 语

本文主要构建了基于SAV方案的二维Allen-Cahn方程全离散格式.在时间方向上采用的离散方法是CN2格式、BDF2格式, 空间上采用重心Lagrange插值配点法离散,应用SAV策略,得到线性无条件能量稳定的数值格式.数值实验结果显示:两种SAV 配点格式均具有高精度的特性,在选取第二类Chebyshev点时具有指数收敛的特性.与经典有限差分格式的误差结果比较可知,重心Lagrange 配点格式采用非常少的节点数即可达到更高精度.