基于嵌套网格的环空流体内旋转杆柱与井筒碰撞特性研究*

岳欠杯, 王笑笑, 曹 文, 刘跃秋, 李 辉, 徐燕璐

(东北石油大学 机械科学与工程学院, 黑龙江 大庆 163318)

0 引 言

浸没在流体中杆管间的接触碰撞是石油工程最常见的现象,由于碰撞引起流体域网格拓扑结构的变化,采用界面解析直接数值模拟方法研究流体中杆管间的碰撞具有很大的挑战,因此尚未得到广泛的研究.

传统的流固耦合数值方法通常是基于贴体网格,最典型的例子是任意 Lagrange-Euler(ALE)界面跟踪方法[1],该方法已得到了广泛的应用[2].在这种方法中,由于网格服从结构形状,可以很容易地定义流固耦合边界,此外,还可以对固体表面附近的网格进行局部细化,在耦合界面附近的数值模拟精度较高.该方法的缺点是在处理大变形和动态边界问题时需要不断更新网格,并在新旧网格上交换各种数据,这不仅增加了计算量,而且降低了求解的精度和稳定性.在具有复杂几何形状的三维空间中,这个过程会相当复杂,特别是当流体中存在固体间接触和碰撞问题时,会出现负体积网格,导致计算终止.为了解决这一难题,国内外学者提出了嵌套网格方法[3],采用灵活的网格耦合方法和对边界条件的处理,将整个流体域划分为包含整个求解区域的背景区域和一个或多个包含固体的组件区域,在每个区域生成高质量的网格,然后进行网格装配,即建立组件网格与背景网格之间的连接,实现各个网格间的数据交换,将背景网格(或组件网格)中供体单元的值通过插值传递给组件网格(或背景网格)中的受体单元.目前,该方法已经广泛成功应用于物体绕流等流固耦合领域.Miller等[4]提出了一种适用于流固耦合分析的嵌套网格方法,并通过对基准测试的数值研究证明了嵌套网格方法相对于传统方法的优越性.基于动态结构嵌套网格方法,李映坤[5]建立了一套多物理场耦合软件平台,对点火过程中的燃气冲击特性、装药传热特性、金属膜片机械响应和隔层变形力学特性进行了深入系统的研究,为脉冲隔离装置的设计、双脉冲发动机的工程研制提供了重要参考.倪同兵[6]生成了由旋翼桨叶贴体网格和背景网格组成的适用于旋翼非定常流场数值模拟的结构运动嵌套网格,从而建立了一套适用于前飞状态直升机弹性旋翼流场与气动特性计算的高精度CFD/CSD耦合方法.徐广[7]对桨叶弹性变形运动的旋翼运动嵌套网格生成方法、高效贡献单元搜索策略、旋翼流场数值模拟和桨叶动力学分析方法等进行了研究,建立了基于Navier-Stokes方程的旋翼非定常流场的数值计算方法和程序.在固体动力学分析中,有限元法是分析物体运动、几何非线性、材料非线性和接触非线性[8]的主要方法.通过调研发现嵌套网格方法与有限元法相结合能有效解决物体绕流、旋翼等流固耦合问题,但用于解决流体域内固体间碰撞问题的研究较少.本文将嵌套网格方法与有限元法相结合,以分域耦合方法对浸没在流体中的旋转杆柱与井筒的碰撞问题进行求解,建立了流体中固体与固体碰撞的数值模拟方法,并与静止流体中球形颗粒和壁面正、斜碰撞实验数据进行对比,证明了本文所建立的数值模拟方法的正确性,据此研究了井筒内旋转杆柱在不同流体黏度、转速条件下的运动与碰撞特性.

1 井筒内浸没在流体中的旋转杆柱力学模型

1.1 模型建立

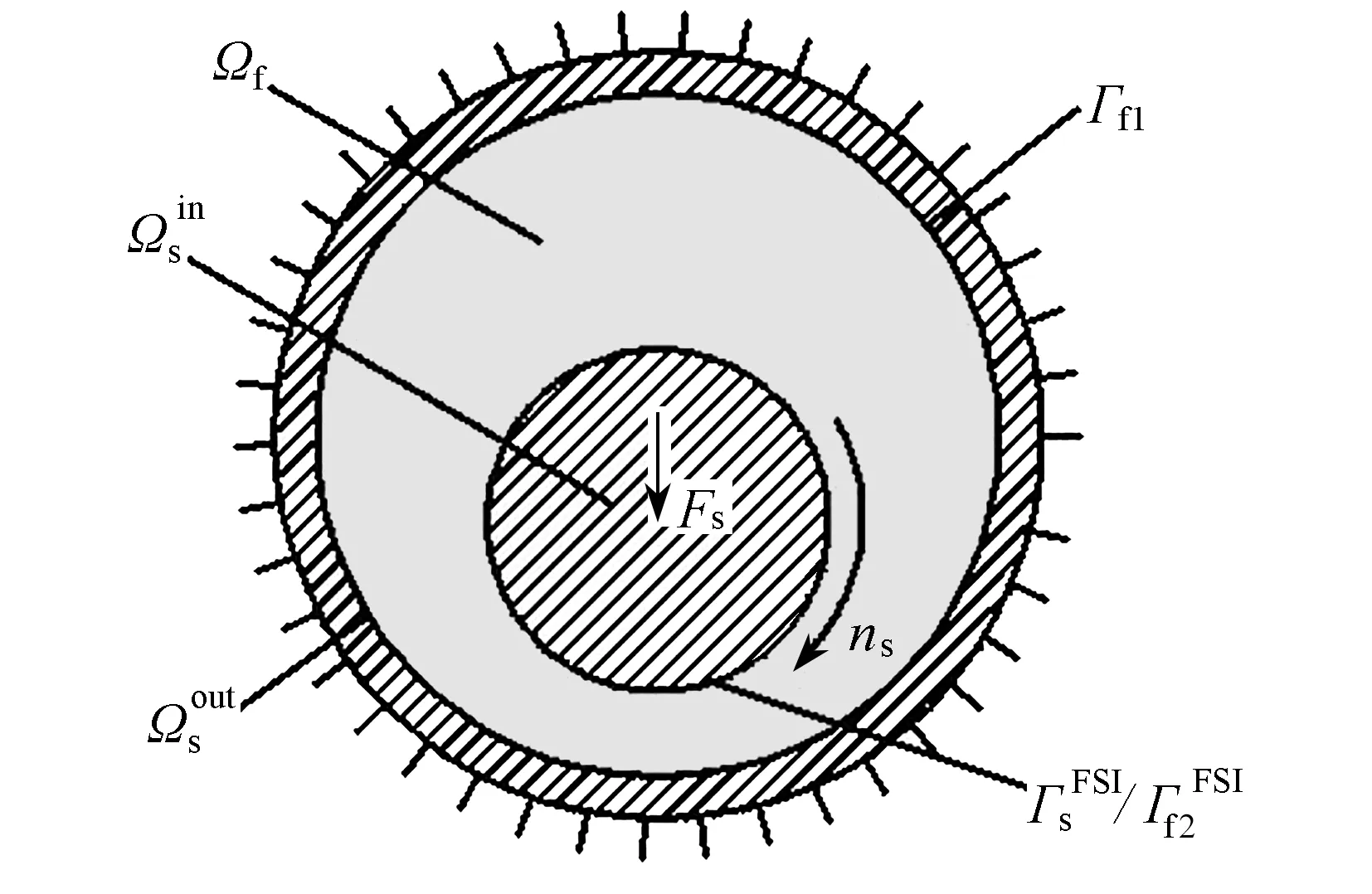
图1 力学模型

模型的边界条件如下:

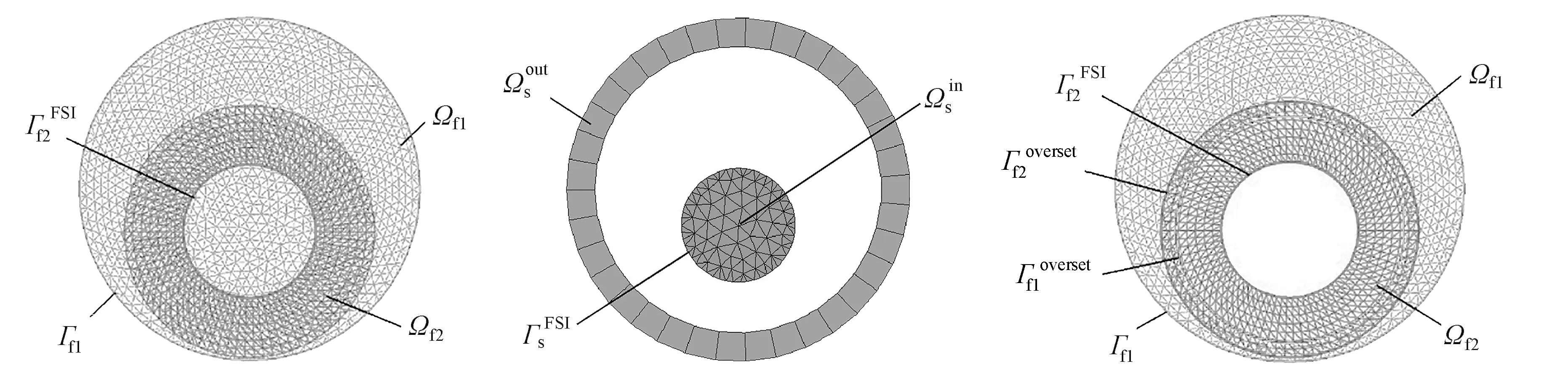
(a)环空流体域 (b)固体域

1.2 环空流体域控制方程

连续性方程为

(1)

式中,ρ为密度,v为速度矢量.

动量守恒方程为

(2)

式中,f代表体积力矢量;p′为修正压力,p′=p+(2/3)ρk;μequ为流体的有效黏度,μequ=μ+μt,μ和μt分别为流体动力黏度和湍流黏度.本文选择使用SSTk-ω模型,其湍流黏度公式[9]为

(3)

式中,k和ω通过湍动能方程和湍动能耗散率方程求得,S是应变速率,a1为常数取值0.31,α*,F2分别为

(4)

(5)

其中,Ret=ρk/(μω),y为场点到最近壁面的距离.

1.3 环空流体域离散方程

背景网格流体域Ωf1的离散方程[10]为

(6)

式中,Af1,Bf1,Cf1,Df1,Gf1分别为背景网格流体域Ωf1的质量、对流、压力、损耗、连续矩阵,其表达式分别为

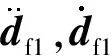
其边界条件为

(7)

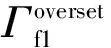
组件网格流体域Ωf2的离散方程为

(8)

其边界条件为

(9)

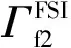
1.4 嵌套网格插值方法

由上述可知,在计算背景网格、组件网格的过程中,需要传递嵌套边界条件,但是在嵌套边界处,两套网格尺寸往往不匹配,因此,要对组件网格与背景网格在嵌套边界处的物理信息进行插值,本文采用3种不同的插值方法[11],具体如下.

1)嵌套边界处网格尺寸相近

当嵌套边界处组件网格和背景网格尺寸相近时,如图4所示,选取边界处任意一对单元,记为单元123,单元abc.若将单元123的信息传递给单元abc,则单元123记为供体单元,单元abc记为受体单元,其插值方法为

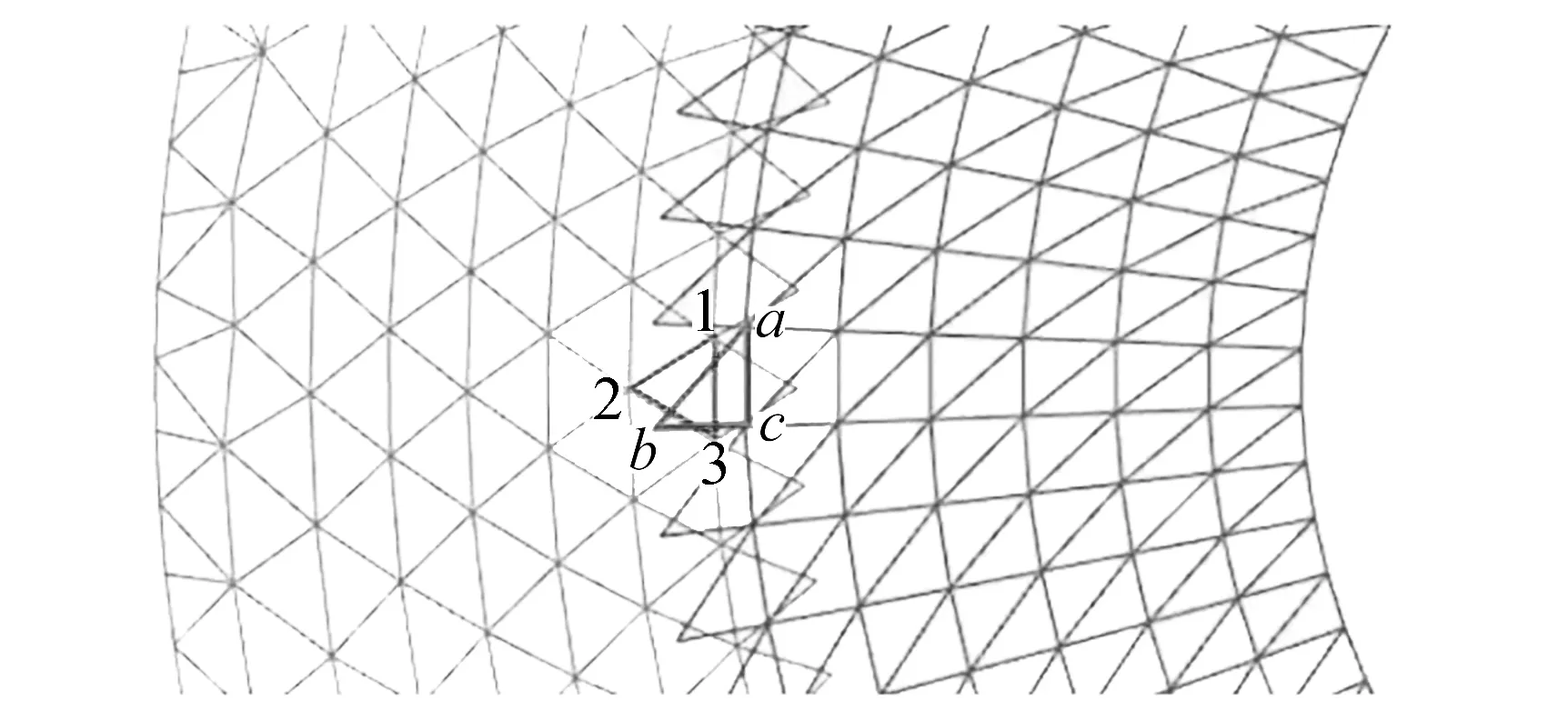
图4 嵌套边界处网格尺寸相近

(10)

2)供体单元尺寸大于受体单元尺寸

如图5所示,123为供体单元,abd,bcd均为受体单元,且单元123的尺寸大于单元abd,bcd的尺寸.以供体单元123传给受体单元abd为例,采用二阶精度对其进行插值,具体过程如下:

图5 供体单元尺寸大于受体单元尺寸

(11)

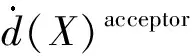
(12)

∑ψi=1, ∑xiψi=xX, ∑yiψi=yX.

(13)

求解式(13)可得各节点的线性有限元形函数.

根据Baker[13]理论,式(11)中f(X)为

f(X)=aψ1ψ2+bψ2ψ3+cψ3ψ1,

(14)

式中,a,b和c为待定系数.利用相邻点4、5、6上的变量求解系数a,b,c,即

(15)

式中,左端矩阵下标1,2,…,6表示插值基函数的取值点;f(Xi)(i=1,2,…,6)为一阶插值结果和节点已有值的误差,

(16)

采用最小二乘法求解即可确定待定系数.确定待定系数后,就可对一阶线性插值进行修正.只要确定单元的线性有限元形函数,其他单元类型的二阶插值误差修正函数计算方法类似.

3)供体单元尺寸小于受体单元尺寸

如图6所示,134,234均为供体单元 ,abc为受体单元,且供体单元尺寸小于受体单元尺寸 ,则受体单元速度插值公式为

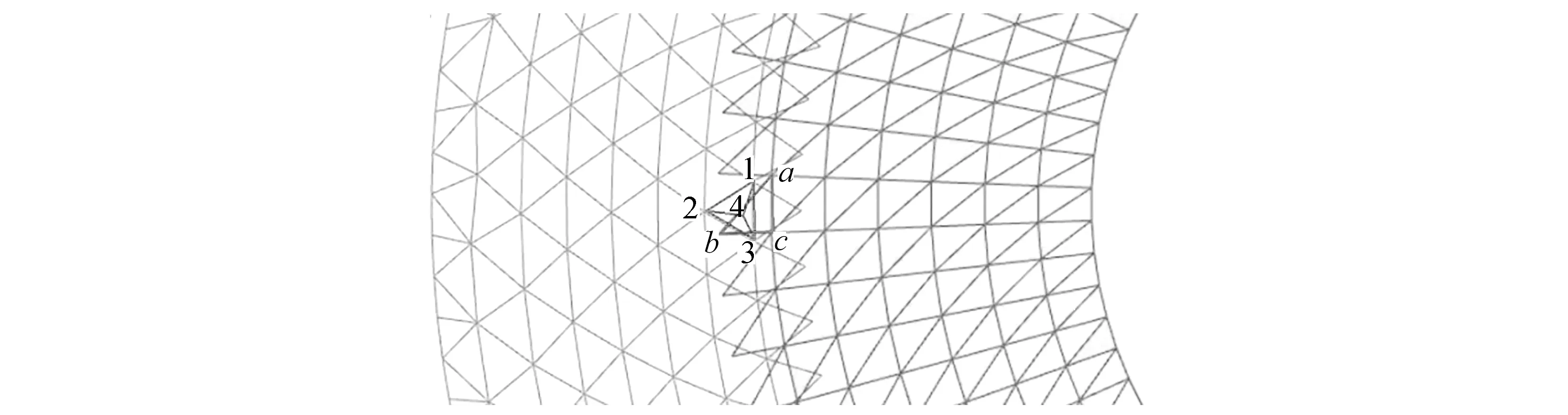
图6 供体单元尺寸小于受体单元尺寸

(17)

式中,θi为供体单元中心到受体单元中心距离的倒数,n为受体单元所包含的供体单元个数.

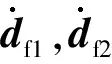
1.5 环空流体域的嵌套网格计算框图

基于上述模型和方法,建立环空流体域嵌套网格计算框图,如图7所示,其具体过程为:

图7 环空流体域嵌套网格计算

1)建立背景网格和组件网格,并设置其边界条件,对模型进行初始化.

2)对背景网格的固体位置处进行挖洞,根据重叠最小化原则确定背景网格和组件网格的范围,基于式(10)、(11)、(17)对嵌套边界处的受体单元进行插值,此过程为背景网格与组件网格的装配.

3)将装配后的背景网格和组件网格赋予新的边界条件,并求解各自流体域方程,当前迭代步结束.

4)下一迭代步在当前迭代步求解的流体域中直接进行背景网格和组件网格的装配,重复步骤2)、3).

1.6 杆柱动力学方程

浸没在流体中的杆柱碰撞的动力学方程[14]为

(18)

式中,M,K,Kc(t),C分别为固体的质量矩阵、刚度矩阵、接触刚度矩阵和阻尼矩阵[15],其具体表达式为

Ff(t)为流固耦合界面上的流体力;Fc(t)为碰撞时的接触力;Fs(t)为固体受到的其他力;ds是固体节点位移矢量.

1.7 流固耦合分域求解耦合界面物理量传递

在本文中,采用分域方法对环空流体域与固体域耦合进行求解.固体域与环空流体域在耦合界面上需传递力和位移信息,分别遵循力平衡和位移协调条件:

Fs=Ff,ds=df,

(19)

式中,Fs和ds为耦合界面固体侧任意一点力向量和位移向量,Ff和df为流体侧对应点的力向量和位移向量.

由于流体网格与固体网格在耦合边界处不匹配,需将耦合界面处的信息进行插值,其具体插值算法见参考文献[16].

1.8 耦合界面上归一化的收敛准则

在流固耦合计算的任一时间步中,耦合界面传递的力、位移信息都需反复迭代,当结果收敛方能进入下一时间步计算,其迭代的归一化收敛准则为

(20)

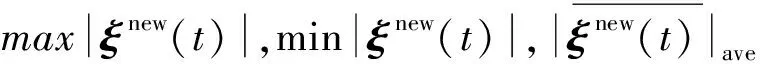
ξjk+1(t)=αξjk(t)+(1-α)ξnew(t).

(21)

1.9 分域求解流程图

基于上述计算方法, 采用分域方法对嵌套环空流体域与杆柱固体域耦合进行求解, 其计算框图如图8所示.

图8 分域求解流程

1)建立固体域模型和流体域(背景网格和组件网格)模型,将组件网格嵌入背景网格,并定义边界条件,假设时间步t已经完成.

2)令jk=0.

3)令jk=jk+1,求解流体域方程(6)和(8),流体域内求解并保持耦合界面位移djk(t)恒定, 由更新后的流场通过式(16)进一步得到耦合界面载荷Fjk(t).

4)将Fjk(t)传递到固体域, 求解固体域方程(18),得到耦合界面位移dnew(t).

5)将dnew(t)传递到流体域,求解方程(6)和(8),得到新的耦合界面载荷Fnew(t).

6)根据收敛准则式(20),若位移dnew(t)与载荷Fnew(t)不能同时满足收敛准则,则返回迭代步3)～5);若不同时满足收敛准则(20),则令t=t+Δt.

7)若t≤tend,则返回迭代步2)～6);否则,迭代结束.

2 嵌套网格数值模拟方法验证

2.1 球形颗粒自由沉降

初始时刻球形颗粒和流体都是静止的,然后球形颗粒开始在重力和水动力作用下做自由沉降运动,流体域大小为[-5D,5D]×[-5D,5D]×[0,80D],并在[-1D,1D]×[-1D,1D]×[0,80D]区域采用相同大小的网格,Δx=Δy=Δz=0.1D,向其他区域过渡时增长率为1.2,其有限元模型如图9所示,球形颗粒物理参数见表1.

表1 球形颗粒物理参数

图9 流体中球形颗粒自由沉降有限元模型

基于上述方法对单个球形颗粒的自由沉降运动进行计算,并与参考文献[15]中的数值模拟和实验结果进行对比.其速度云图和速度随时间变化曲线分别见图10、图11.

(a)浸入边界法(文献[15]) (b)嵌套网格

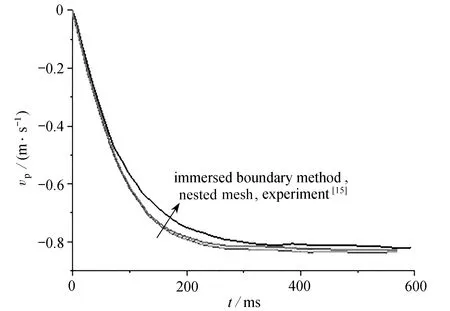
图11 颗粒垂向速度vp随时间的变化

由图10和图11的结果对比可知,当垂向速度vp为-0.7 m·s-1时,采用本文方法得到的云图与浸入边界法云图基本一致,且颗粒的垂向速度随时间变化曲线与实验、浸入边界法曲线基本吻合.因此可验证本文建立的嵌套网格数值方法对球形颗粒自由沉降过程的计算是正确的.

2.2 球形颗粒与壁面正碰撞

流体域为长方体,其几何尺寸长、宽、高分别为40 mm,40 mm,170 mm;建立流体域网格如图12所示,在底部壁面处采用局部网格加密,且壁面处第一层网格高度为0.01 mm,边界层增长率为1.1.玻璃板厚度为12 mm,划分了4层单元,且玻璃板底面为固定约束.球形颗粒材料为钢材,密度为7 800 kg·m-3,弹性模量为2.4×1011Pa,Poisson比为0.3,其计算工况见表2.

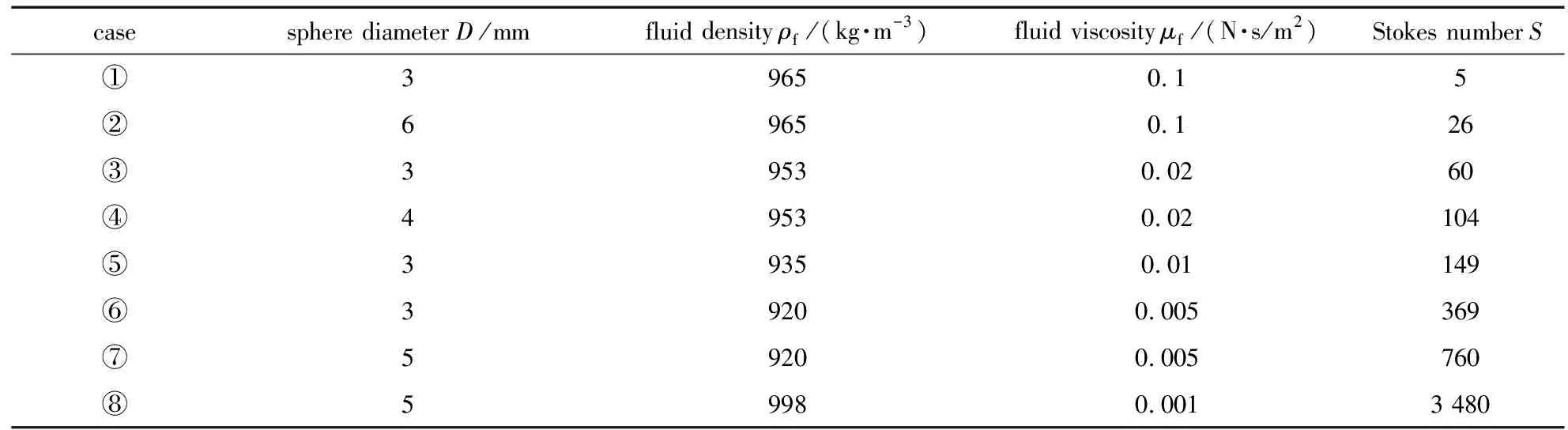
表2 球形颗粒与流体的物理参数

图12 流体中球形颗粒与壁面碰撞有限元模型

对表中不同工况下球形颗粒与壁面碰撞和反弹过程进行计算,得到球形颗粒恢复系数e与Stokes数S的关系变化数值,并与Gondret等[17]的实验结果进行对比,对比曲线如图13所示.

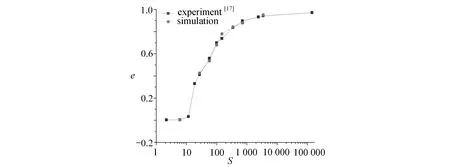
图13 恢复系数e与Stokes数S的关系曲线

从图13中可以看出,当S小于10时,球形颗粒不反弹,随着S逐渐增大,恢复系数逐渐趋向于球形颗粒干碰撞时的恢复系数,且数值模拟与实验数值吻合较好,表明本文建立的数值方法对流体中固体与固体碰撞的模拟是可行的.

图14为工况⑤球形颗粒与玻璃壁面碰撞和反弹过程中高度、速度随时间的变化曲线,取相对时间t=0 s为球形颗粒与玻璃壁面第一次碰撞时间.

(a)高度 (b)速度

由图14可知,由于流体黏性耗散和材料阻尼导致动能损失,球形颗粒后续的反弹高度越来越低,且反弹速度亦越来越小;数值模拟能够很好地展现该工况的运动趋势,且其数值与实验数据吻合,表明本文建立的数值方法对流体中固体与固体正碰撞的模拟是准确的.

图15为工况⑤球形颗粒与壁面正碰撞和反弹过程中流体涡量场随时间的变化云图.由图15可知, 当球形颗粒下降时, 由于速度逐渐增大尾迹涡环也逐渐增大, 而且球形颗粒在尾迹位置开始出现与尾迹涡环方向相反的涡量.当t=-0.011 s时, 颗粒距壁面较远, 颗粒仍处在加速过程中; 当t=-0.002 s,即球形颗粒与壁面距离约为颗粒半径时,流体被挤出间隙,壁面处产生与颗粒尾迹涡环方向相反的涡量;当t=0 s时,颗粒第一次与壁面碰撞; 当t=0.002 s时,反弹过程中的颗粒通过主尾迹环向上运动并形成方向相反的二次涡环; 当t=0.039 s时,颗粒第一次反弹到最大高度,由于黏性耗散,颗粒周围的初始涡环减小;当t=0.084 s时,颗粒回落并第二次与壁面碰撞.

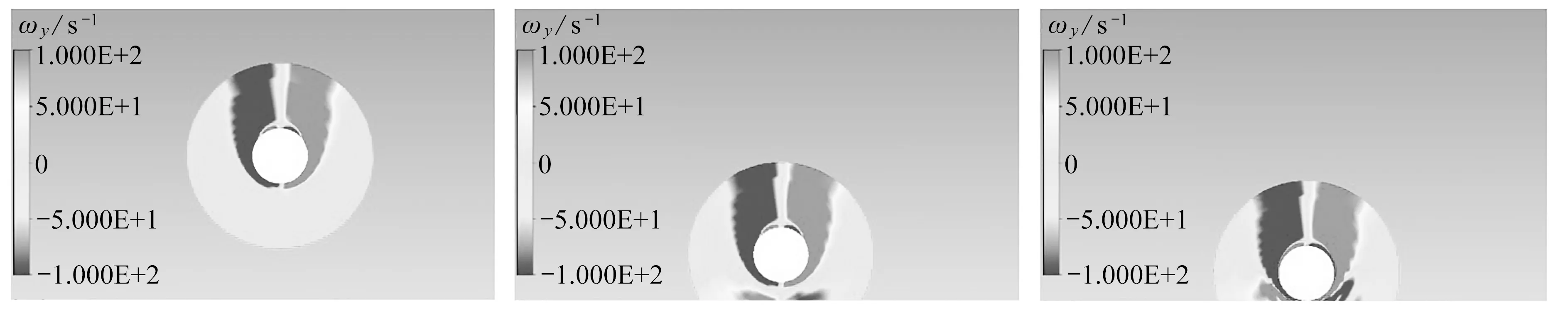
(a)t=-0.011 s (b)t=-0.002 s (c)t=0 s

2.3 球形颗粒与壁面斜碰撞

基于上述方法对流体中球形颗粒与壁面斜碰撞和反弹过程也进行了数值模拟,流体域仍为长方体,其长、宽、高分别为60 mm,60 mm,50 mm, 建立网格如图16所示,边界层尺寸为0.01 mm,增长率为1.2,模型与Joseph和Hunt[18]实验中使用的颗粒和黏性流体的物理参数相同,见表3.

表3 球形颗粒与流体的物理参数

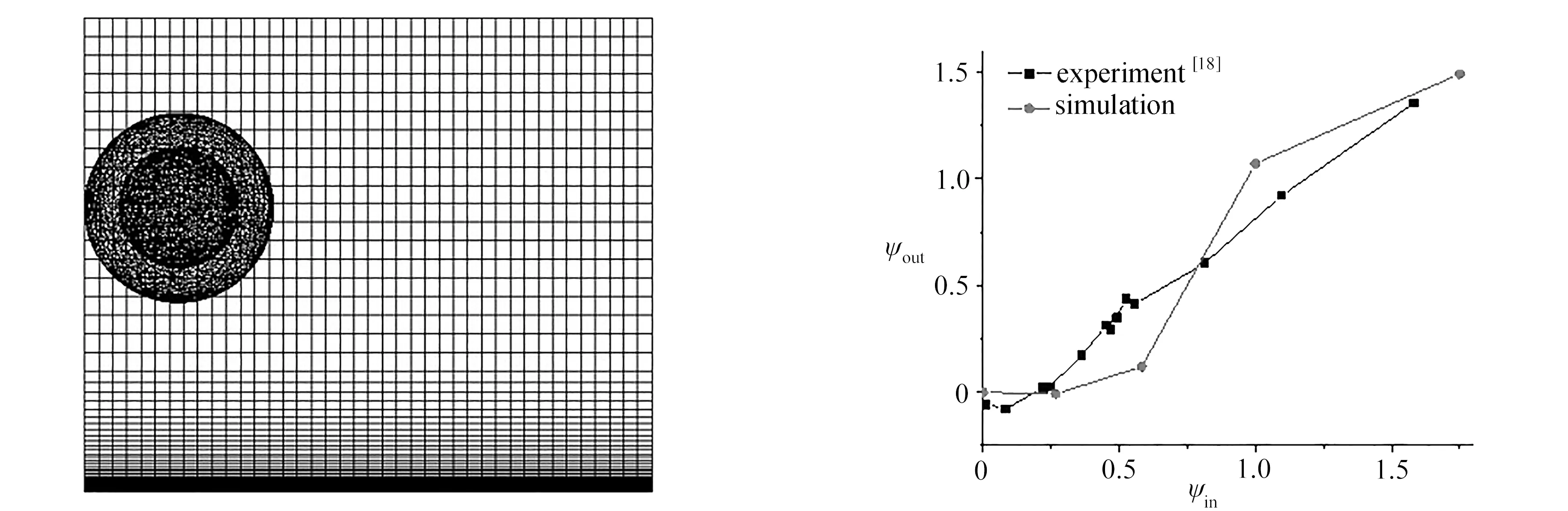
图16 流体中球形颗粒与壁面斜碰撞有限元模型 图17 无量纲化入射角和反射角关系曲线

经计算,得到球形颗粒在流体中与壁面斜碰撞的无量纲化入射角与反射角变化结果,并与Joseph和Hunt[18]的实验结果进行了对比,对比曲线如图17所示.图中ψin=tanθin,θin为小球碰撞点的入射角,ψout=etanθout,e为弹性恢复系数,θout为小球碰撞点的反射角.因受小球转动速度的影响,tanθout=(vT-vω)/vN,vT为小球平动速度沿着壁面的速度分量,vω为小球转动速度,vN为小球平动速度垂直于壁面的速度分量,即无量纲化反射角ψout与小球平动速度和转动速度直接相关.

由图17可知,球形颗粒反射角随入射角增大而增大,且数值模拟结果与实验结果基本吻合,由此可验证采用本文方法对流体域中固体斜碰撞的数值模拟的正确性.

图18为入射角θin=45°时球形颗粒与壁面斜碰撞和反弹过程中涡量场随时间的变化云图.由图18可知,当t=-0.004 2～0 s时,流体的涡量场与球形颗粒与壁面正碰撞工况的分布相似,不同的是其涡量场倾斜了一定角度;当t=0.003 s时,球形颗粒反弹,下落时尾迹的初始涡环以相同的角度撞击壁面,并在颗粒周围出现一个新的涡环; 当t=0.003～0.007 9 s时,部分初始涡环随着球形颗粒移动而逐渐脱落,直至分离.

(a)t=-0.004 2 s (b)t=-0.003 s (c)t=0 s

3 环空流体内旋转杆柱与井筒碰撞计算结果

基于上述方法对1.1小节井筒内浸没在流体中的旋转杆柱与井筒的碰撞进行数值计算,计算参数见表4.

表4 旋转杆柱和流体的物理参数

3.1 有流体与无流体计算结果对比

由表5可知固体域2 109个网格与3 234个网格第一次碰撞力变化不大,所以固体域划分为2 019个网格,如图19(a)所示;流体域105 396个网格和137 991个网格第一次碰撞力变化不大,所以流体域划分为105 396个网格,边界层尺寸为0.01 mm,增长率为1.2,如图19(b)所示.

表5 网格无关性验证

图20为有环空流体和无环空流体旋转杆柱与井筒碰撞力随时间的变化曲线,井筒内环空流体随杆柱运动产生的涡量如图21所示.

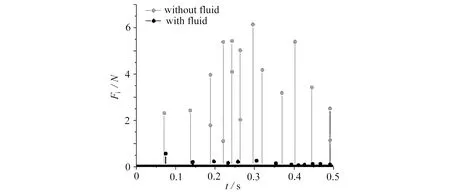
图20 旋转杆柱与井筒碰撞力随时间的变化

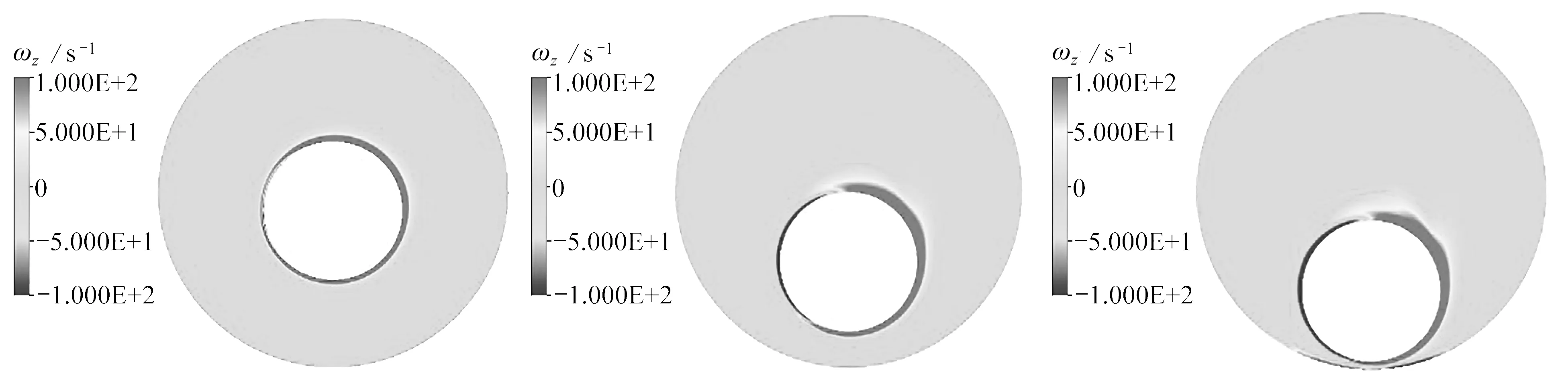
(a)t=0.03 s (b)t=0.06 s (c)t=0.071 1 s

由图20可知,井筒与杆柱环空内无流体时,杆柱与井筒间的碰撞力最大值为6.13 N,而环空内有流体时,其碰撞力仅为0.56 N.即环空无流体时,杆柱与井筒间碰撞时的碰撞力数值明显大于有流体的工况.因此,当井筒内有流体存在时,杆柱与井筒的碰撞剧烈程度明显降低.

由图21可知:当t=0.03 s时,流场受杆柱转动影响出现涡量;到t=0.06 s时,受杆柱运动速度影响产生相反的涡量;t=0.071 1～0.074 1 s时,涡量场和小球正碰撞壁面相似;但当t=0.11 s杆柱上升到最高位置时,涡量场主要受转速影响,杆柱平动速度的影响几乎可以忽略;当t=0.142 s时,杆柱产生第二次碰撞.

3.2 黏度对环空流体中旋转杆柱与井筒碰撞的影响分析

为探讨流体黏度对环空流体中杆柱与井筒碰撞特性的影响,对流体黏度分别为0.01 N·s/m2,0.02 N·s/m2,0.03 N·s/m2,0.04 N·s/m2,0.05 N·s/m2进行计算,得到杆柱与井筒间碰撞力随时间的变化曲线,如图22所示.图23为杆柱上第1次与井筒碰撞点的运动轨迹,图24为杆柱中心点速度随时间的变化.

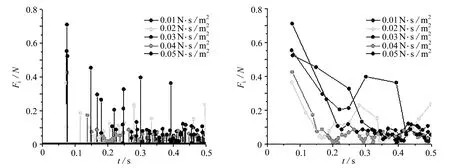
(a)碰撞力随时间变化 (b)碰撞力连线

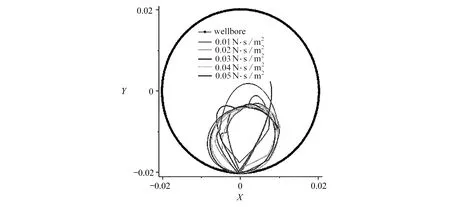
图23 不同流体黏度下杆柱上与井筒第1次碰撞点的运动轨迹

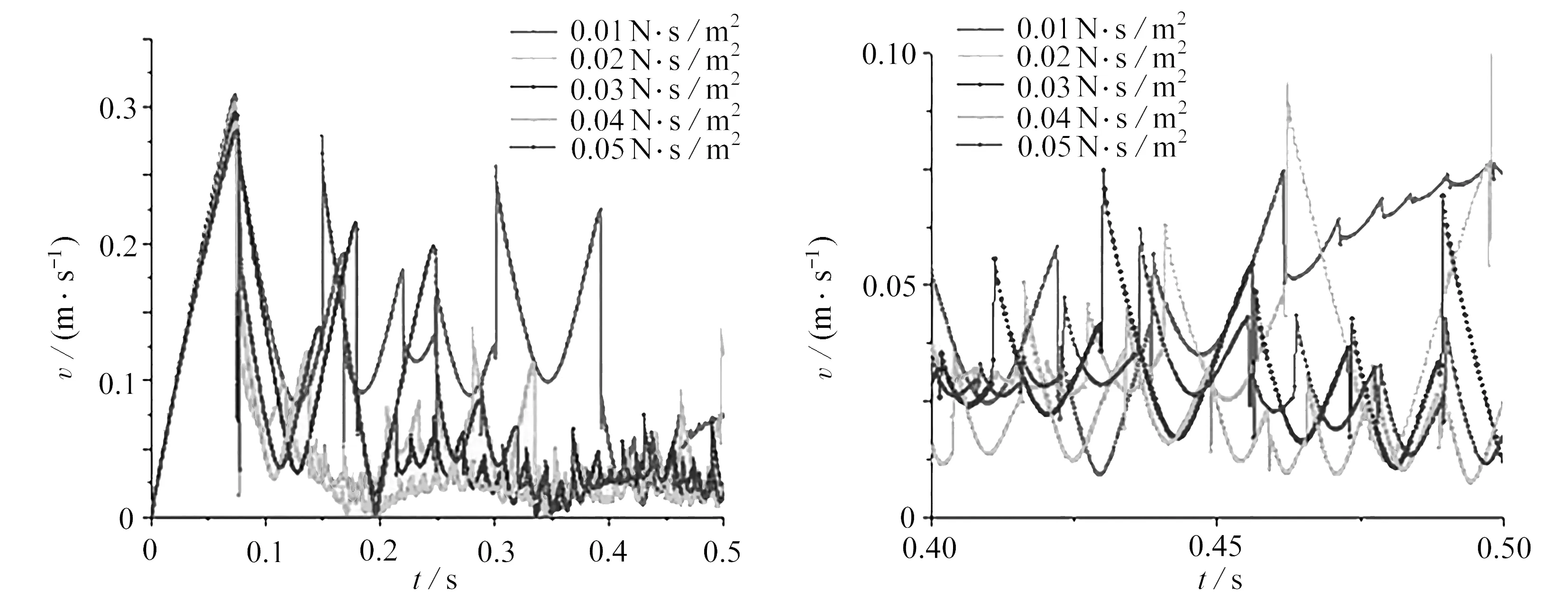
(a)0～0.5 s (b)0.4～0.5 s

由图22(a)可知,杆柱与井筒初始碰撞时碰撞力数值较大,且最大值不受黏度影响,随着时间推移碰撞力数值逐渐减小,且受黏度的影响越来越明显,其数值随着黏度增加呈下降趋势.由图22(b)可知,当黏度为0.01 N·s/m2,0.02 N·s/m2时,碰撞力波动下降,当黏度为0.03 N·s/m2,0.04 N·s/m2,0.05 N·s/m2时,杆柱与井筒碰撞力呈单调下降,黏度越大下降趋势越明显,其数值减小至0.1 N.

由图23可知,杆柱上第1次与井筒碰撞点的运动轨迹随黏度增大越来越趋于圆形,即杆柱运动范围与黏度负相关,黏度越大,运动范围越小,其轨迹越趋于圆形.

由图24(a)可知, 杆柱中心点速度随时间推移整体呈下降趋势, 当杆柱与井筒发生碰撞时, 其数值产生突变, 且速度的振荡程度和流体黏度成负相关, 黏度越低振荡越剧烈.由图24(b)可知,当黏度大于0.03 N·s/m2时,中心点速度在0.4 s后趋于稳定,且呈周期性变化.

3.3 转速对环空流体中旋转杆柱与井筒碰撞的影响分析

为探讨杆柱转速对环空流体中杆柱与井筒碰撞特性的影响,对杆柱转速分别为12.56 rad/s,18.84 rad/s,25.12 rad/s,31.40 rad/s,37.68 rad/s进行计算,得到杆柱与井筒间碰撞力随时间的变化曲线,如图25所示.图26为杆柱上第1次与井筒碰撞点的运动轨迹,图27为杆柱中心点速度随时间的变化.

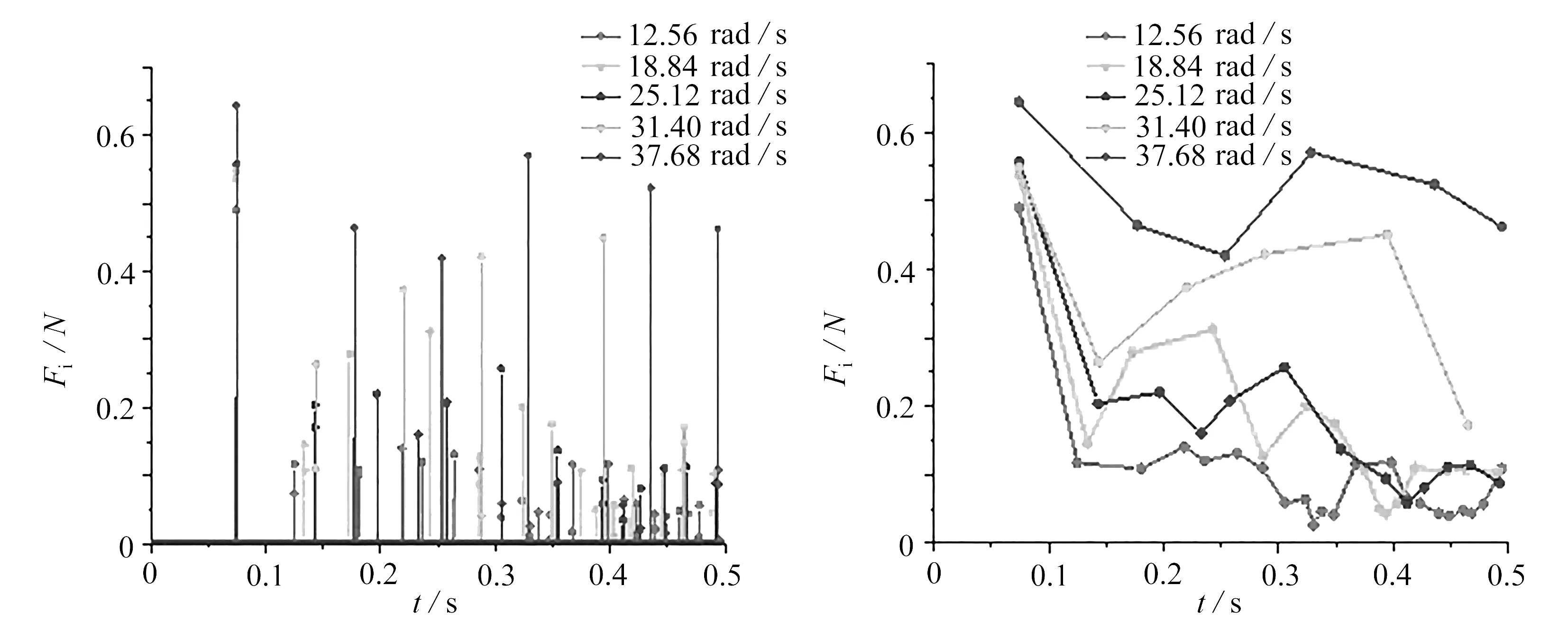
(a)碰撞力随时间变化 (b)碰撞力连线

图26 不同转速下杆柱上与井筒第1次碰撞点的运动轨迹 图27 不同转速下中心点速度随时间的变化

由图25(a)可知,杆柱与井筒间的碰撞力随杆柱转速增大而增大,随时间推移整体呈下降趋势.由图25(b)可知, 当转速为12.56 rad/s时, 0.1 s后碰撞力变化趋于平缓; 当转速为18.86 rad/s和25.12 rad/s时,0.35 s后碰撞力变化趋于平缓,其数值仅为0.1 N;当转速为31.40 rad/s和37.68 rad/s时,碰撞力始终在较大范围内变化.

由图26可知,杆柱运动范围与杆柱转速正相关,即转速越大,其运动范围越大.由图27可知,杆柱中心点速度的振荡程度与杆柱转速成正相关,即转速越高振荡越剧烈.当杆柱转速大于25.12 rad/s时,杆柱中心点速度不再随时间推移整体呈下降趋势,其数值在杆柱与井筒碰撞点处产生突变.

4 结 论

1)为研究环空流体内旋转杆柱与井筒的碰撞特性,基于嵌套网格和分域求解算法,本文建立了井筒内浸没在流体中的旋转杆柱力学模型,将环空流体域离散为相互嵌套的背景网格和组件网格,并推导两套网格间边界条件信息插值公式,采用分域耦合算法对固体域与流体域耦合进行求解.该方法能够避免流体域网格拓扑的改变,有效解决了传统贴体网格方法在求解流体中存在固体间碰撞问题时网格易出现负体积的问题.

2)基于上述方法,对静止流体中的球形颗粒与壁面正、斜碰撞进行数值计算,并与实验结果进行对比,验证了本文数值计算方法对流体域中固体与固体间碰撞模拟的正确性.

3)对不同流体黏度、不同杆柱旋转速度下杆柱与井筒碰撞特性进行了研究,结果表明:杆柱与井筒间碰撞力随黏度增大而降低,杆柱运动范围与流体黏度负相关;随着杆柱旋转速度增大,杆柱与井筒间的碰撞力增大,杆柱运动范围与其转速正相关;且当杆柱与井筒发生碰撞时,杆柱上任一点速度出现突变.本文计算方法可为下一步研究石油工程领域中杆管柱偏磨、脱扣、断裂失效提供一种行之有效的手段.