基于SOLO理论的高中物理圆周运动模型建构能力的评价

摘 要：为了在新课改背景下更好地开展高中物理教学，教师需要对高中生的物理建模能力进行评估。传统的教学评估往往是对学生进行书面测试，无法全面体现学生的物理建模能力，而SOLO分类理论能够对高中生的物理深度学习给出比较准确的评价。文章以SOLO理论为基础，通过教学案例分析，提出相应的教学优化策略，以期对学生物理建模能力和核心素养的培养起到一定的促进作用。

关键词：SOLO理論；高中物理；圆周运动；建构能力；评价

作者简介：常轩（1989—），女，甘肃省兰州市第五十中学。

一、相关概念的定义和内涵

（一）物理模型

“模型”一词的基本含义是指浇注的形状，根据物质的形态和结构，对被研究的对象进行必要的简化，用合适的形式或规律来描述其基本特点，从而形成模型。建立模型方便对客观事实进行分析，从而为实际问题的进一步求解提供帮助。用通俗的话来说，模型就是一种象征或某种形式。在物理学中，物理模型是对物理现象和物理规律等的抽象表达，强调其中主要的、关键的因素。

在物理学中存在许多复杂的问题，而要想了解其中的规律，就必须撇开问题的次要因素，抓住主体、突出本质，这就是物理建模。这是一种更精确、方便、科学的思考物理学问题的方式。在高中阶段，学生在学习和应用物理模型的过程中，必须明确各种模型的适用条件，然后根据现实情况来判断应该使用哪些模型。

（二）SOLO理论

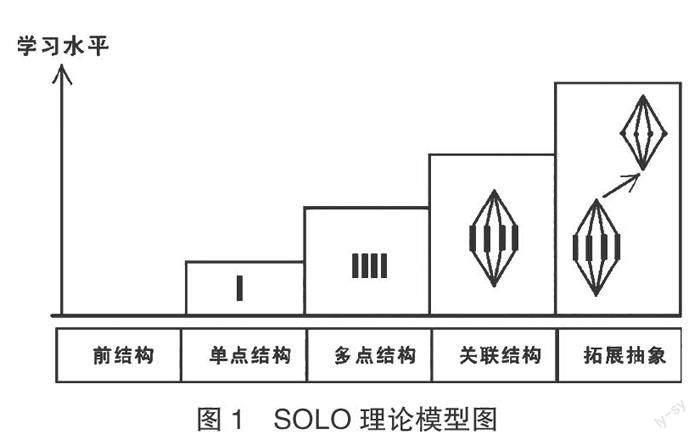
SOLO意为可观察的学习结果的结构。香港大学教育心理学教授比格斯在研究中意识到皮亚杰发展阶段论的限制，因而为有效判断学生的思维层次提出了一种系统化的评价方法，即SOLO分类评价法。这一理论突破了认知结构无法测量的限制，通过学习结果对学习者的知识层次进行评价，从而使学习者的思维结构变得可见、可测、可评价。根据皮亚杰的认知层次理论，SOLO分类理论将学习者的思维结构分成五个层次：前结构、单点结构、多点结构、关联结构、抽象扩展结构。在一定意义上，SOLO分类理论可以揭示学习者的整体学习质量。

（1）学生尽管注意力集中在前结构（P）任务上，但是会受到早期阶段或非模型的不相关因素的影响或误导。

（2）单点结构：学生的注意力聚焦于有关区域，然后在某个方面进行拓展。

（3）多点式结构（M）：学生找到更多与问题相关的正确思路，但是不能将其整合在一起。

（4）关联结构：学生能将不同的思路组合成一个体系结构。

（5）抽象拓展（E）：学生将思路结构抽象化，能深化并拓展问题。

在此基础上，按照五个层次所对应的学习特征，结合它们的差异和关联，得出SOLO理论模型，见图1。

二、SOLO分类理论与深度学习

从SOLO分类理论的角度出发，将学生的思考水平分为五个层次：前结构、单点结构、多点结构、关联结构、抽象拓展结构。在实际教学中，教师需要有机整合SOLO分类理论和深度学习评估。

目前，深度学习研究方兴未艾，是当前科学教育领域的热门话题，它的特征是注重学习者对知识的理解、整合、建构、反思和迁移应用。新时代背景下，物理学科教学需要重视对学生物理学科核心素养的培养，为实现这一目的，教师需要一些具体的教学路径。经过专业的理论研究、教学实践以及优秀教师的调查研讨，深度学习被证明是培养学生核心素养的有效方法之一。在深度学习评估中，最重要的就是将学生的知识理解层次展现出来，帮助学生将浅层知识转化为更深层次的知识。SOLO分类理论是一种评估体系，它以学习活动为基础，SOLO分类理论中的前三个层次都是浅层学习的表征，第四层次的关联结构和第五层次的抽象拓展是学习者对知识的深层理解，包括复杂的认知活动。

深度学习与教学评估是当前教育领域的一个重要课题，而SOLO分级评估可以从师生之间的多维对话、问题解决、批判的自我监督等方面来判断学生的发展水平，并能帮助教师改善课堂教学方法，提高学生的深度学习思维和深度学习能力，实现学生物理学科核心素养的提升，从而实现以评促学、以评促发展。

三、圆周运动模型及其建构过程

（一）圆周运动模型

不同的圆周运动模型有各自的特性，体现在受力情况、临界条件等方面。圆周运动基础物理模型都和现实生活密切相关，这些模型中的受力情况都有很大的不同，需要学生自己去感受和理解，而不是死记硬背。

（二）圆周运动模型建构过程

要更好地理解模型，需要对模型建构过程有一定的认识。圆周运动模型的建构过程包括：问题形成、系统特征因素确定、模型架构确定、模型建立、模型真实性验证。以下是具体步骤。

问题形成：从真实情境中抽象出有研究意义的物理问题。

系统特征因素确定：基于对问题的初步研究，总结与问题本质关系最紧密的相关因素，即最有代表性的要素，作为建构物理模型的关键。

模型架构确定：依据已掌握的主要要素，忽视次要要素，突出本质，确定物理模型的基本架构和理论指导。

模型建立：依据特性因素和物理规律，建立相应的物理模型。

模型真实性测试：基于建构好的物理模型，引入数据进行测试，以验证实际情况与所构建的模型是否相符、是否满足其基本特征和规则。

四、评价研究

高中物理把物体的运动划分成直线运动和曲线运动两种形式，大部分学生对直线运动的认识和应用都比较好，但对曲线运动的理解和应用就显得有些吃力了，特别是学习到圆周运动时，学生们的物理素养常常会显现出较大差距。因此，圆周运动模型的建构是非常重要的，对于培养学生的物理思维和物理问题解决能力具有十分积极的作用。

（一）SOLO理论视角下的试题分析

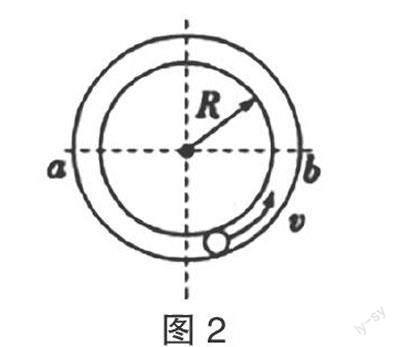
如图2所示，小球在竖直放置的光滑圆形管道内做圆周运动，管道内侧壁半径为R，小球半径为r，则下列说法中正确的是（  ）

A.小球通过最高点时的最小速度vmin=g（R+r）

B.小球通过最高点时的最小速度vmin=0

C.小球在水平线ab以下的管道中运动时，内侧管壁对小球一定无作用力

D.小球在水平线ab以上的管道中运动时，外侧管壁对小球一定有作用力

题目解析：这道题的正确答案是B、C。本题需要学生对小球在管道内进行圆周运动的过程中的受力情况进行分析，并以此求解。虽然这是一道选择题，但是教师可以从学生的答题情况判断学生对这一圆周运动物理模型的掌握情况，并根据SOLO理论进行评级。如果学生选择了B选项，那就意味着学生知道这是一个圆周运动模型，并且知道小球运动的特性和临界状态，说明这些学生的思维层次已经具备了多点结构。选择C选项的学生，他们的能力较强，能够对圆周运动模型中小球的受力情况进行全面分析，从而判断出小球在特定位置的状态，他们的圆周运动模型建构能力与SOLO分级中的关联结构相匹配。如果学生选择了其他选项，则说明他们的思维层次还比较低，没有实现深度学习。

（二）SOLO评价标准

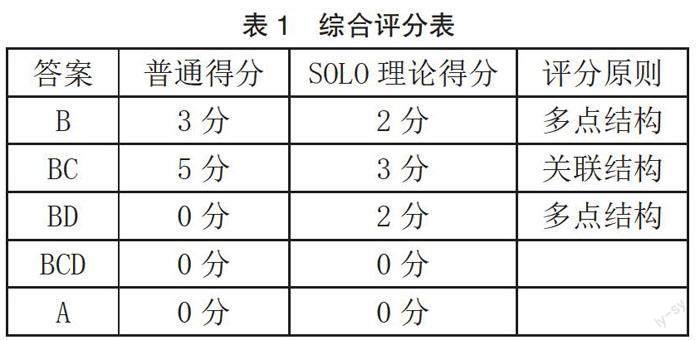
根据每个选项包含的知识点，相应的圆周运动模型建构能力也被划分为不同的层次。教师要做的就是打分，然后统计学生的成绩，从而分析他们的思维水平（如表1），从而更好地对学生进行评估和分析。综合评分表上记录有普通得分和SOLO理论下的得分，以此体现SOLO理论原则以及它与一般评分标准的区别。

对于基本的评分标准，教师根据每个选项所占分值给出相应的分数，而SOLO理论评分则存在着一定的差异。一般情况下，体现出单点结构思维层次的回答可以得1分，这意味着学生可以从这个问题中获得一些有用的信息，并且了解物理模型；体现出多点结构思维层次的回答可以得2分，这说明学生在弄清楚物理模型类型的基础上，能够精确地构建物理模型；体现出关联结构思维层次的回答得3分，这说明学生能够较好地利用物理模型来解决物理问题。

（三）评价结果

这一问题是多项选择题，它不但要求学生分析垂直平面上的圆周运动，建立圆周运动模型，还要求学生能分辨出这个圆周运动模型是绳模型还是杆模型。对于杆模型，学生需要了解其运动特征、临界条件以及运动过程中各个部件对球施加的力，以此进行问题求解。

五、教学建议与反思

（一）教学建议

物理是一门非常考验学生的思维逻辑的学科，学习物理必须要有悟性，要善于思考，努力理解和分析问题的本质，只有不断地思考与领悟，才能真正理解物理规律。所以，在物理教学中，教师必须教会学生构建物理模型，从而提高学生的学习效率。

在日常教学中，教师要运用物理基础模型来进行物理问题的分析与求解，并从物理概念、物理现象、物理情境等方面研究物理问题，找到物理基本规律，并掌握物理模型的建构条件以及求解物理问题的方法和技巧。根据SOLO理论评估结果，在教学实践中，教师要针对不同能力层次的学生进行专门的指导，力求使每个学生的能力层次都能获得有效提升。如果学生能找到物理问题的关键，就能把自己所熟知的理想化物理模型提取出来，慢慢地建立起学习自信心。

（二）反思

教育教學的主要目的是培养学生的深度学习能力和深层思考能力，这也是教师教学的两个基本问题。运用SOLO分类理论对以上教学过程进行评估，可以看出SOLO理论的每个思维层次都能在学生的解题思路和答题上有所体现，说明SOLO理论在评价高中生的物理建模能力方面具有较好的应用性。此外，教师应该意识到当前的SOLO理论研究还不够成熟，还需要根据实际教学情况不断优化理论以及有的放矢地应用教学评价方法。

结语

目前仍有很大一部分高中生的物理建模能力不佳，造成了他们学习高中物理难度大等问题。物理本身是一门非常有趣的学科，涉及许多有趣的自然现象，教师要加强对学生的指导，运用生动形象的物理模型，使学生感受到学习物理的乐趣，并在此基础上运用SOLO理论来有效判断和评价学生的物理建模水平，促进学生学习能力的提高，帮助他们建立学习自信心。

［参考文献］

贲志学.SOLO分类理论下高中物理深度学习评价研究［J］.数理化解题研究，2022（6）：80-82.

冯翠典，高凌飚.现状与反思：SOLO分类法国内应用研究十年［J］.教育测量与评价（理论版），2009（11）：4-7，11.