基于两种NN的CRH3动车组辅助逆变器故障诊断

孟建军,徐妍琰,李德仓,王鑫健

(1. 兰州交通大学机电技术研究所,甘肃 兰州730070;2. 甘肃省物流及运输装备信息化工程技术研究中心,甘肃 兰州 730070;3. 甘肃省物流与运输装备行业技术中心,甘肃 兰州 730070;4. 上海铁路局上海动车段,上海 201200)

1 引言

辅助逆变器是CRH3型动车组辅助供电系统的重要组成部分。辅助供电系统既要为牵引电机提供强迫风冷,为动车制动用提供压缩机的维持动车安全运行的所需负载又要提供照明、制冷制热、动车组内日常电器的稳定和安全使用的电力,保障其能正常使用[1]。在动车组作为客运主导的今天,动车组的运行不仅仅呈现于动车运行的快速和平稳上,动车组内日常生活电器的安全使用得到有效保障更加展现了一个国家工业的高度发达[2]。由此观之,辅助逆变器的供电质量与可靠性是影响到动车运行安全和旅客乘坐舒适度的最直接因素[3]。因此对辅助逆变器故障诊断进行深入细致的研究,对我国高速动车组安全可靠运行至关重要。本文以CRH3型动车组辅助逆变器为研究对象,运用MATLAB/Simulink软件建立辅助逆变器仿真模型,对辅助逆变器在不同IGBT开路故障状态下进行了仿真研究,通过选择合适的小波基对电流输出波形进行小波分解重构,得到电流小波的能量频谱,对能量系数进行数据处理和重构,提取辅助逆变器的故障特征向量,将小波分解提取的特征向量汇总作为输入,对故障进行编码作为输出,采用BP与GRNN神经网络进行故障识别,建立对应的故障诊断模型,分别对BP与GRNN进行训练和测试,对比两种算法的测试结果,发现GRNN网络较BP网络提高了迭代速度和精度,可以有效的提高故障诊断的精确率。

2 CRH3型动车组辅助逆变器工作原理

辅助逆变器一般分为电压源型和电流源型,CRH3型动车组上安装的是电压源型逆变器,电压源型逆变器按照其输出电压电平数不同,分为两电平式和三电平式,CRH3型动车组采用的是两电平式[4]。两电平式逆变器拓扑结构是由六个开关管T1、T2、T3、T4、T5、T6构成的三相全桥,具体结构如图1所示。设三个桥臂开关函数Si公式为

表3 测试结果

图1 辅助逆变器主电路图

(1)

当同一桥臂两个开关管两者的状态是相反的关系,当一方导通时,另一方断开。计算可得,由SA、SB和SC可以组合成2*2*2=8种电路工作模式。

3 辅助逆变器仿真

CRH3型动车组的辅助逆变器采用先逆变后降压式的“直-交”型结构[5],其结构拓扑如图2所示。辅助逆变器直接从主变流器的中间环节取得DC3000V电压,经逆变,再经过滤波,最后得到为440V/60Hz的三相交流电压。

图2 辅助逆变器结构拓扑

根据上述辅助逆变器主电路图及结构拓扑,在MATLAB/Simulink中搭建如图3所示逆变器仿真模型,参数取自CRH3型车辅助逆变器实车运行数据,其中输入DC3000V,输出3AC400V/60Hz。

图3 辅助逆变器仿真模型

仿真采样步长设置为1*10-5,仿真时间共为0.6s,0.5s时开始触发,仿真采用ode23t 算法。启动仿真模型时,调节相关的各个参数,在仿真开路故障时,通过对相应的脉冲置 0 来模拟某一开关管的故障,将得到辅助逆变器在不同故障情况下的输出电流波形。

由于三相桥式逆变电路中IGBT很少有三个及三个以上同时发生故障,因此本文只分析一个、两个IGBT同时发生开路故障的情况。由于篇幅原因,以最具代表性的T1故障、T1T2故障、T1T3故障、T1T4故障这四种情况为例分析其波性特征。

辅助逆变器IGBT单管故障分析:T1管故障,如图4(a)所示,当 T1管发生故障时,A相电流输出的波形正半周期基本全为负值, B、C相电流输出波形正半周期的幅值超过负半周期且有部分畸变。

图4(a) 辅助逆变器T1管故障波形

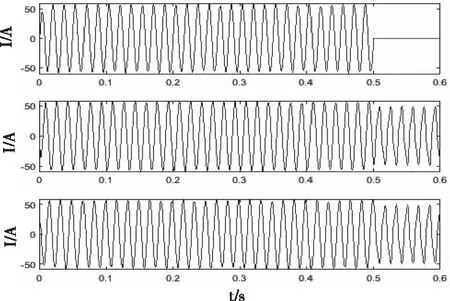
图4(b) 辅助逆变器T1T2管故障波形

图4(c) 辅助逆变器T1T3管故障波形

图4(d) 辅助逆变器T1T4管故障波形

辅助逆变器同一桥臂两个IGBT同时故障:T1T2管故障,如图4(b)所示,T1T2管故障时,其中一相的电流输出信号基本全部消失,其余两相的输出电流有部分畸变,且正半周期和负半周期的幅值有所降低。

辅助逆变器两相同一位置两个IGBT同时故障:T1T3管故障,如图4(c)所示,当T1T3管发生故障时,A、B相电流输出的波形负半周期基本全为正值,C相电流输出的波形与A、B相呈相反状态。

辅助逆变器两相交叉位置两个IGBT同时故障:T1T4管故障,如图4(d)所示,其中一相电流输出的波形正半周期基本全为正值,另一相电流输出的波形与之呈相反状态,而其余那相电流输出波形有部分畸变。

4 小波变换故障特征提取

传统的信号处理经常运用傅里叶分析,然而在实际应用过程中发现其存在大量的应用问题,人们通过各种研究探索对其进行改进,创造了STFT(短时傅立叶变换)[6]。由于STFT采用的滑动窗函数在选定后为固定的,因此导致了其时间分辨率是无法改动的,当滑动窗选取较窄时采集到的信号比较短,会导致频率分辨率的降低。当滑动窗较宽时导致时域上并不够精准,缺乏其自身所具备的自适应能力。因此小波变换[7]成为一种改进的时频局域化分析方法,小波窗口的面积相等、时间和频域窗口可以进行变化,它的出现成为信号分析领域的突破性进展。

(2)

在式(2)中,a表示伸缩因子,b表示平移因子[8]。

对式(2)中参数a,b进行展开后,可以计算出任意时刻任意精度的频谱,但如果在每个可能的尺度下一一计算小波系数将会产生庞大的数据计算量,因此需要将其离散化。将连续小波进行离散化操作被称为离散小波变换(DWT)。

为了更好的实现小波变换,需要通过计算机来辅助计算同时把连续小波ψa,b(t)和连续小波变换Wf(a,b)离散化。小波离散化不会将时间离散化,只针对连续的伸缩因子a和连续的平移因子b,与t无关[8]。

在连续小波中,需要考虑函数

(3)

在式(3)中b∈R,a∈R+,且a≠0,ψ是容性的,为了计算方便,在连续小波离散化过程中令a取正值,相容性条件则表示为

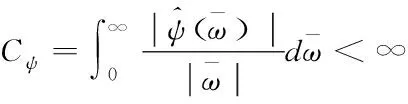
(4)

(5)

所以离散化小波变换系数的求解公式为

(6)

重构公式为

(7)

C为常数,取值与信号无关[9]。

动车组的运行环境复杂,造成信号中的谐波复杂多变,使得信号中含有非周期信号、畸变信号等成分。而小波变换在对这类谐波信号的处理上有着天然的优势,在变换中能够很好地将这些成分去除掉。当辅助逆变器处于正常运行时,其输出电流为三相正弦波。而故障运行时,由于故障部分电流信号的丢失,造成系统输出波形不对称,波形中出现许多畸变信号。经过分析CRH3型动车组辅助逆变器故障诊断研究,选择恰当的小波进行分解来处理故障信号,得到需要的特征信号。

以下以T1管故障为例,将输出电流利用db3小波进行8层分解并重构后,获得了1个低频a8和6个高频d1、d2、d3、d4、d5、d6、d7及d8,如图5、6所示。

图5 T1故障时A相小波分解图低频部分

图6 T1故障时A相小波分解图高频部分

通过小波分解波形按照不同频带分离滤波,在不同故障情况下,其各频带组成会有所不同。将三相电流波形利用小波分析方法进行8层分解,得到了8个高频带和1个低频带,其中低频量很好的表现了波形特征,可以作为一个求解特征向量参数,称这种为能量系数特征向量。能量系数求解过程如下:

1)进行小波分解,提取各频带分解系数,再进行重构;

2)求解各分解系数能量值。公式为

(8)

式中,j=1,2,3,4,5,6,7,8;k=1,2,…,n;n的长度由系数长度决定。

当j=9时,有

(9)

3)选取合适的能量值组成特征向量

N=[E1E2E3E4E5E6E7E8E9]

4)归一化处理特征向量;

其中,在步骤(3)中涉及到能量值的选择时发现,可以计算出低频部分占据了信号的大部分能量,高频能量值占总能量比例较小,因此对能量向量进行数据处理如下

(10)

则有N=[E1/EE2/EE3/EE4/EE5/EE6/EE7/EE8/EE9/E]

按照该方法,对其种故障的进行特征向量提取,由于篇幅限制,这里仅给出T1故障、T1T2故障、T1T3故障、T1T4故障这四种情况特征值,得到如表1所示的数据。

表1 不同故障时各频带能量占总能量比例

步骤4中归一化处理能量系数特征向量时发现,如果依然采取恒定的总能量值E来归一化处理三相能量时,虽然计算方便,但是在实际运行中存在问题。本文中解决这一问题的方法是通过动态的计算每个采样周期内的归一化处理系数P来分别对每段采样周期信号进行处理。其中P的计算方式

P=max([Ea8A,Ea8B,Ea8C])+

0.1*(Ea8A+Ea8B+Ea8C)/3

(11)

不同故障状态下的输出电流能量系数有所差别,大部分能够简单分辨出来,但有些组的其中一部分能量值还是难以区分因此,需要再找其它特征向量。因此采用提取小波重构后的输出三相电流中正侧波形平均值与正侧、负侧(绝对值)平均值和的比值来作为特征向量。利用这一特点,可以提取出比例系数Q,其表达式所示

(12)

根据上述能量系数提取方法,在MATLAB中是通过程序代码运行得到结果。每个状态共提取出40组特征值。特征值数据过于庞大,以最具代表性的正常、T1故障、T1T2故障、T1T3故障、T1T4故障进行展示见表2。

表2 不同故障状态下故障特征向量

5 BP与GRNN神经网络故障识别

5.1 BP神经网络

误差逆传播(BP算法)是目前运用最为广泛的神经网络学习算法,其结构如图7所示。当外部产生一信号传到这个网络中时其输入层最先得到信号,随后经隐含层传递至输出层处理,这个过程被称为前向传递。有前向传递就会有反向传播。反向传播就是将前向传递的结果与期望相比,从而以此为根据不断调整权值和阈值。通过不停的学习调整,最终使输出值无限靠近期望值[10]。

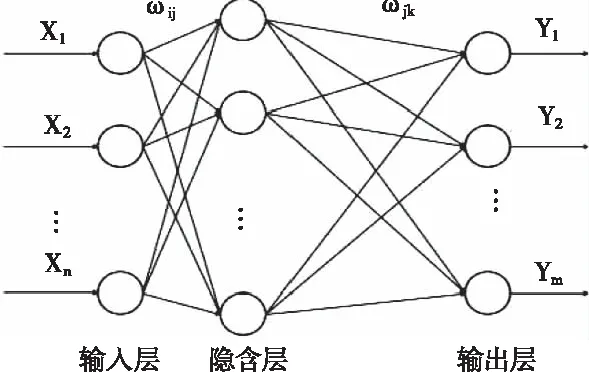
图7 BP神经网络结构

如图7所示X1,X2,…,Xn为输入值,Y1,Y2,…,Ym和为权值。以非线性函数比网络,则自变量便是输入值,因变量为预测值。于是网络就存在一个映射关系,是从n个自变量到m个因变量,而它存在的条件就是确定了输入和输出节点数分别为n和m[10]。如果BP网络选择的算法是沿梯度下降法,会有很多弊端例如训练次数多、收敛不够快等。本文采用改进的BP神经网络算法即LM算法(trainlm)。其中n代表输入层神经元个数,由故障特征向量的维数来确定,所以n=6; m代表输出层神经元个数,由故障编码的维数来确定,因此m=6。隐含层神经元的个数尚无法精准确定,常常使用"试错法"进行寻找。运用试错法分别对不同隐含层个数进行测试,发现当隐层节点数为27的时候,网络MSE值最小。

把之前得出的数据分成训练与测试样本进行测试。图8所示发现迭代12次后达到要求,验证误差为0.00015354,网络未发生过拟合。

图8 trainlm函数训练结果

5.2 GRNN神经网络

广义回归神经网络(GRNN)属于径向基网络[11],不过改进之处在于其以RBF神经网络为模型基础,多了一个求和层,因此收敛速度就快,非线性逼近能力也强,适合处理预测问题。样本数据少,也有很好的效果,同时还能处理不稳定数据。在处理分类和拟合问题上,尤其是数据不足以很好反映实际问题的时候有着很大的优势。

不同于BP神经网络的三层结构GRNN神经网络包括输入、隐含、求和、输出四层[12]。GRNN神经网络是一个前向传播网络,其优点在于它无须反向传播求模型参数。网络结构图如图9所示。

图9 GRNN神经网络结构

在进行故障识别之前,先确定其网络的整体结构。得到输出层节点数是6个,因为故障特征向量是6维。隐含层为径向基层,节点数个数等于训练样本数,由网络自适应确定。求和层中分子与分母单元输出的商值,经由输出层得到输出值,从故障识别编码中能够得出,输出层有6个节点。将已得到的故障特征输入网络,进行了四次交叉验证实验,如下图10所示。

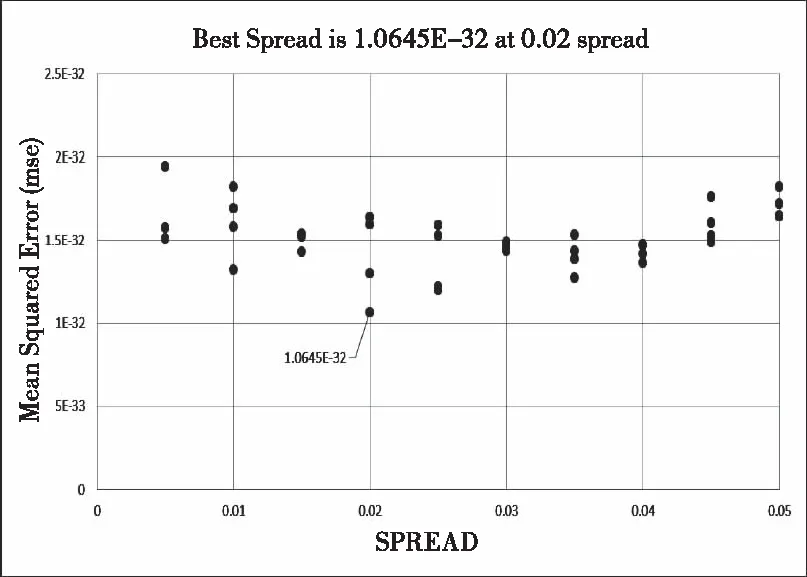
图10 GRNN函数训练结果

通过采取交叉验证的方法去找到最佳SPREAD值,以达诊断效果最佳的目的。最终得出在第二次交叉验证中SPREAD为0.02时最佳,1.0645E-32即为最小均方差MSE。

5.3 结果对比分析

BP神经网络采用LM算法进行多次运算,经过研究得到迭代9-12次时效果最佳,GRNN神经网络采用交叉验证方法,通过反复训练后确定交叉验证次数为4时,找到的SPREAD 值最佳。

以样本T1故障测试结果进行对比分析,根据表3能够直观的看出相比于BP神经网络,GRNN 神经网络实际输出值与期望值之间的误差平均提高了40个数量级,在识别精确率上远优于BP神经网络,提升了故障诊断的准确率,更好的实现诊断。

在训练时间上,对比如下表4所示,为了故障诊断的精度提升,GRNN神经网络采用交叉验证的方法,因而LM算法训练的BP网络训练时间与GRNN网络训练时间相比,两者差别不大。

表4 神经网络对比

6 结论

最终从研究结果可以得出:

1)本文通过详细的分析与合理的选择确定了db3小波基来进行操作所得出的故障特征向量,能够较好的呈现出其中的故障信息,并验证了故障特征向量的正确性。

2)本文采用的BP与GRNN神经网络均能够实现故障识别,LM算法训练的BP神经网络训练时间与GRNN神经网络相近,GRNN神经网络无需对权值处理,使其处理速度较快,因此略好于 BP神经网络。

3)在识别精确率上,GRNN 神经网络实际输出值与期望值之间的误差远远小于BP神经网络,提高了故障识别的精度,诊断结果更为准确。