航天器接近高斯混合模型固定时间控制方法

朱效洲,王 祎

(1. 军事科学院国防科技创新研究院,北京 100071;2. 南京电子技术研究所,江苏 南京 210039)

1 引言

近年来,以在轨维护等为背景的航天器近距离接近成为航天器协同控制领域研究的热点。任务航天器在对故障航天器进行在轨维护时,既要能够在指定时间内接近目标,又要避免与目标发生碰撞。

接近目标所需时间,即协同控制的收敛速率,是控制系统设计时需考虑的主要因素之一。文献[1,2]等可在有限时间内实现控制系统收敛,但对调节时间的估计依赖于系统初始状态,极大地限制了其应用范围。固定时间控制(Fixed-time control,FTC)[3]可确保系统收敛时间与初始状态无关,但无法解决状态约束问题。

接近过程中的碰撞避免,即协同控制的安全性,是控制系统设计时需考虑的另外一个主要因素。同时,避撞问题也是一种典型的状态约束问题。文献[4,5]等将避撞问题转化为带约束的优化问题,使用优化算法设计轨迹,但过高的计算量限制了其应用。为降低计算代价,人工势函数(Artificial Potential Function,APF)[6]方法被广泛使用,解决了简单外形目标的避撞问题[7,8]。然而,复杂外形目标的避撞问题仍需解决。

为解决有限时间内复杂外形目标航天器的安全接近问题,本文提出一种高斯混合模型固定时间控制(Gaussian Mixture Model based Fixed-time control, GMM-FTC)方法。

2 航天器相对运动动力学模型

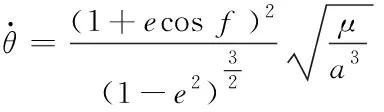
(1)

(2)

则任意椭圆轨道上,非线性相对运动的状态转移矩阵[9,10]可描述为

(3)

其中

(4)

(5)

3 高斯混合模型固定时间控制

3.1 复杂外形目标航天器建模

假设复杂外形目标航天器表面有N个采样点组成的点云Ζ={Zi=[xi,yi,zi]T},使用高斯混合模型对其进行表示,则某采样点Zi满足

(6)

(7)

为获取复杂外形目标航天器表面采样点云的高斯混合模型,首先使用K均值算法[11]进行聚类,确定点云的K个初始聚类中心,随后使用Expectation-Maximization(EM)算法[12]迭代对参数集Θ进行估计。

3.2 固定时间控制

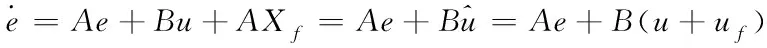
(8)

其中

(9)

(10)

其中

在此基础上,使用固定时间控制FTC[3]来确保调节时间,控制参数ε、ς和γ以及相应系数计算如下

p1(q)=1,p2(q)=3+q

(11)

非线性坐标变换sFTC定义为

sFTC-i=yi+φFTC-i,(i=1, 2)

(12)

其中

(13)

由式(12)和(13)可知,式(10)等价于

(14)

其中

ξ(y1,y2)=A21y1+A22y2+

(15)

yi(j)(i=1, 2)是yi(i=1, 2)的第j个元素。

切换面渐进律定义为[13]

(16)

(17)

其中|·|表示绝对值。

因此,FTC的控制律为

(18)

3.3 基于高斯混合模型的固定时间控制

基于对复杂外形目标航天器的建模,本文在传统人工势函数APF[6]基础上,提出一种新的基于高斯混合函数的势函数

(19)

其中P和M是正定增益矩阵。并进一步将固定时间控制FTC[3]与基于高斯混合模型的势函数相结合,提出高斯混合模型固定时间控制方法GMM-FTC。其非线性坐标变换定义为

sGMM-FTC-i=yi+φGMM-FTC-i,(i=1, 2)

(20)

其中

(21)

ks是正定增益矩阵,∇表示梯度,∇rφ是基于混合高斯模型的势函数φ相对于任务航天器位置矢量的梯度。

根据式(20)和(21),式(10)等价于

(22)

其中

ξGMM-FTC(y1,y2)=

(23)

切换面渐进律定义为

(24)

其中SGMM-FTC-2(j)是SGMM-FTC-2的第j个元素,函数f(SGMM-FTC-2,αi)定义为

(25)

因此,GMM-FTC的控制律为

(26)

3.4 李雅普诺夫稳定性分析

定义李雅普诺夫函数

(27)

则有

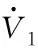
(28)

其中λi-min=min(λij)(j=1, 2, 3)。

可知

(29)

因此,根据李雅普诺夫定理,GMM-FTC有限时间内稳定,且可以确保从任意初始状态可在有限时间TGMM-FTC内到达表面S(t)

(30)

此外,根据式(21),控制误差y1和y2有限时间内可在终端切换面收敛为0。

4 数值仿真

4.1 仿真环境

图1所示为具有复杂外形(带有凸出天线和太阳能板)的目标航天器以及LVLH坐标系中任务航天器的相对运动路径。仿真中,任务航天器从起始位置(星号1)出发,到达目标航天器天线附近的终点位置(星号2)。目标航天器和任务航天器的物理参数见表1,任务航天器在LVLH坐标系中的初始状态见表2。

表1 目标航天器和任务航天器物理参数

表2 任务航天器在LVLH坐标系中的初始状态

图1 目标航天器以及LVLH坐标系中任务航天器的相对运动路径

假设仿真的期望状态为Xf=[-5 -0.913043 -0.304348 0 0 0]T;控制加速周期和积分步长均为1s,终止时间为400s;地球引力常数为3.986×1014m3/s2

将本文提出的GMM-FTC方法用于有限时间内复杂外形目标航天器的安全接近,并与FTC[3]方法、原始APF与FTC结合的APF-FTC方法进行仿真比较分析。仿真中的控制增益和参数如下所示,FTC、APF-FTC和GMM-FTC使用相同的公共参数。

对于GMM-FTC,高斯混合模型由10个分量组成,其初始聚类中心为

4.2 仿真结果和分析

由初始聚类中心开始,先使用K均值算法[11]进行聚类,再使用EM算法[12]进行迭代求解,获得目标航天器外形的高斯混合模型表示,并通过采样,以点云形式进行显示,如图2所示。可以看出,虽然目标航天器具有复杂的外形,高斯混合模型仍可以很好地进行表示。

图2 目标航天器点云形式显示

图3所示为目标航天器的天线与任务航天器间最小距离,棕色虚线圈中的部分放大后在图右上角进行展示,红色线表示判断碰撞是否发生的临界线。由图可知,GMM-FTC、APF-FTC可以解决复杂外形条件下目标航天器的避撞问题,而FTC发生碰撞。

图3 天线与任务航天器间最小距离

图4所示为控制误差随时间变化情况,由图可见APF-FTC虽能避撞,但任务航天器被推离目标航天器,GMM-FTC相比APF-FTC控制精度更高。

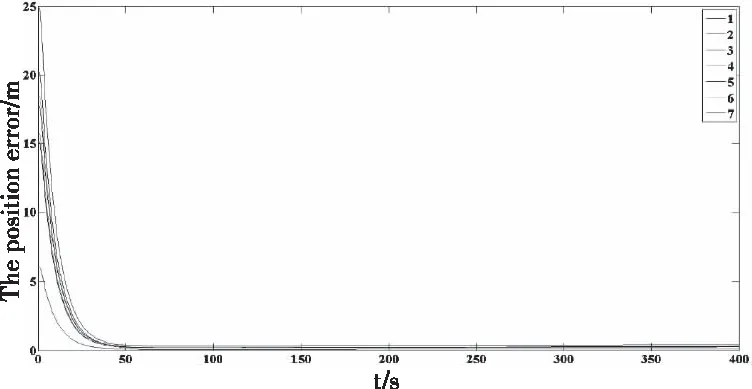
图4 不同初始位置条件下的位置误差

图4 控制误差随时间变化情况

使用相同控制参数,任务航天器从表3所示的7个不同初始位置出发,GMM-FTC的位置误差如图4所示。由图可知,不同初始位置条件下用时相同,表明GMM-FTC可以确保调节时间与初始状态无关。

表3 LVLH坐标系下任务航天器不同初始状态

5 总结

为解决有限时间内复杂外形目标航天器的安全接近问题,本文提出一种高斯混合模型固定时间控制方法GMM-FTC。该方法使用混合高斯模型对复杂外形目标进行参数化表示,并将所提基于高斯混合模型的势函数与有限时间控制相结合。李雅普诺夫稳定性分析及仿真结果证明了方法的稳定性和有效性。