基于VMD-RL-LSTM的短期风功率预测

谷学静,陈洪磊,孙泽贤,张 怡

(1. 华北理工大学电气工程学院,河北 唐山 063210;2. 唐山市数字媒体工程技术研究中心,河北 唐山 063000)

1 引言

风能作为一种清洁的可再生能源,具有无污染、清洁性、资源充足的特点,在世界能源领域占有越来越多重要的比例[1]。精确的风功率预测可以降低电网的旋转备用容量,有利于降低其运行成本及风电对电网的负面影响[4]。

风功率预测的方法主要包括三大类:物理方法、统计方法及两种方法组合的方法[5],数值天气预报模型(NWP)是物理方法之一,此方法利用气象实况条件来进行预测,但是因为天气预报数据更新频率低、数值气象模型复杂,一般不用于短期风功率预测[6]。研究历史风电功率数据的规律一般使用统计方法,建立非线性间映射关系,从而使时间序列预测历史风力数据得到实现。由于机器学习、强化学习和深度学习近年来的快速发展,机器学习、强化学习和深度学习[9]模型比以前的模型得到了更精确的结果。支持向量机(SVM)[11]和人工神经网络(ANN)[14]这两者都有非线性的特点,成为常用的机器学习预测模型。强化学习可以通过“试错”的外部环境找到最佳的实施策略[18],并加强学习将其应用于需求响应,形成一个完整的决策感知系统,能够有效地帮助确保问题的答案以可靠性和准确性为导向。随着深度学习的发展,长短期记忆网络(LSTM)不仅可以挖掘输出变量与相关输入变量之间的时空相关性,而且在复杂时间序列预测领域也得到了极大的发展[19]。目前,结合机器学习/深度学习技术的混合模型已经被证明是更为可靠的预测模型。

张东英等[20]对风电功率概率预测的定义预测方法和控制策略进行了综述;Wang等提出了将经验模态分解(EMD)算法应用于风速预测模型[21];当一个单一的模型预测风速时,它往往存在精度差的问题,越来越多的研究者开始研究组合模型。文献[22]通过构建CEEMDAN、VMD和AdaBoost的RT-ELM混合模型,能够有效解决风速时间序列的非线性问题,从而提高预测的准确性。王静等提出了基于CEEMD和GWO的超短期风速预测,两种方法的结合能够有效改变支持向量回归机参数的预测模型,进而得到优化[23]。文献[24]推荐了一种利用LSTM网络进行超短期风功率预测,考虑多个不同NWP数据的输入,预测精度高于传统的神经网络。为了改进LSTM存在泛化能力差、容易造成过拟合等问题,李艳等提出了一种CNN-LSTM网络模型进行风电功率预测[25],利用CNN提取序列特征的能力有效提取子集,在删除干扰内存的数据后在LSTM上输入数据,进而较长的记忆信息能够得到保留,解决梯度弥散问题。

通过对文献的分析得出以下结论。分析表明,数据分解技术的应用有效降低样本噪声干扰并显著提高模型的预测性能。总体而言,在风功率预测方面,混合模型比单一模型预测更加可靠、有效。

本文提出了一种基于变分模态分解(VMD)、强化学习(RL)参数寻优和长短时记忆网络(LSTM)的短期风功率预测方法。变分模态分解不仅能够消噪,还可以将原始信号的核心成分进行保留,分解后的效果较好。强化学习方法可以从实际系统的学习体会和经验中进行调整策略,这是一个慢慢地逼近最优策略的过程。它在进行学习的过程中无需导师进行监督。参数优化可以优化LSTM模型的参数,使模型预测精度更加精确。LSTM神经网络是传统RNN的改进版本,它在处理短期和长期依赖关系的问题时更加健壮。实例分析表明,混合模型可以有效提高短期风电功率精度。

2 研究方法

2.1 变分模态分解

K.Dragomiretskiy和D.Zosso提出了一种新型复杂信号分解时频分析方法,即变分模态分解。它可以将原始时间序列s(t)分解为有限带宽的不同分量uk(t),根据预设的模态数,对应的中心频率为ωk,通过交替迭代更新找到约束变分模型的最优解,避免在迭代过程中遇到的端点效应等问题。利用变分模态分解,能够将非线性和非平稳信号得到有效的处理。对比于EMD,解决了其端点效应和模态分量混叠的问题,该算法可表示为[26]

1)对每一个uk(t)进行Hilbert变换得到单侧频谱

(1)

2)将模式的各个分析信号与估计的中心频率e-jωkt相乘,频谱移到基带

(2)

3)利用高斯平滑估计对解调信号梯度L2进行正则化,可得出模态函数的各个带宽,约束变分模型如下表示

(3)

4)随着二次罚因子α和拉格朗日乘子λ的引入,原始时间序列在高斯噪声影响下的信号重构精度s(t)得到了保证,并将抑制变分问题转化为无抑制变分问题

(4)

5)使用交替方向乘子法(ADMM),将分量uk(t)、中心频率ωk和拉格朗日乘子λ进行求解更新,扩展拉格朗日函数表达式的最低点,更新过程如下

(5)

(6)

(7)

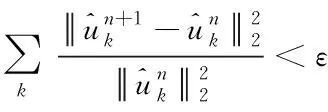
(8)

2.2 强化学习

强化学习(reinforcement learning,RL)在机器学习领域中是被用来解决连续性的决策问题,它是指通过与环境的交互和学习而获得的知识,自主进行的动作和选择,通过不断的试错获得最优策略[27]。强化学习的重要特征是:通过强化学习来解决和处理这个问题的各种可能性目标都被简单地作为一个标量来进行奖励,强化学习的主要目标就是通过外部环境产生的奖励,而不是Agent本身。所有强化学习都涉及映射学习,该学习将环境的状态或姿势映射到适当的动作或动作的一般分配,这种映射称为策略。它指示在当前学习期间每个状态代理应采取的行为。

在强化学习的情况下,Agent的某种行为策略会带来环境奖励,模型如图1所示。

图1 强化学习基本模型

2.3 LSTM神经网络

LSTM神经网络是循环神经网络(recurrent neural network,RNN)的一种,由于梯度爆炸或梯度消失的问题,RNN不适合长期依赖的任务[28]。它们只能解决短期依赖性任务,而LSTM可以有效地学习长期依赖性任务。

LSTM是一种适合于时间序列预测问题的深度学习体系结构。LSTM单元的内部状态存储器提供了先前相关信息的内部存储。细胞的输入、输出和遗忘门负责通过细胞的信息流动。LSTM在这些门的帮助下处理和存储相关信息。图2显示了LSTM细胞的内部布局。LSTM单元的数学是使用等式(9)-(14)定义的。

图2 LSTM单元结构

ot=σ(Woht-1+Uoxt+bo)

(9)

it=σ(Wiht-1+Uixt+bi)

(10)

ft=σ(Wfht-1+Ufxt+bf)

(11)

st=tanh(Wht-1+Uxt+b)

由此可以看出SCADA系统的局限性：SCADA系统提供的数据只能作为参考值，并不能直接应用于电力运行的参数设值；SCADA系统提供的数据有部分干扰值，需要人工进行正确的判断；SCADA系统只能实现有限数据的采集与监测。

(12)

st=ft⊙st-1+it⊙st

(13)

ht=ot⊙tanh(st)

(14)

式中,xt,st,st,ht分别表示时间步长t时的网络输入状态、网络状态、暂态状态和输出状态。it表示输入门,ot表示输出门,ft表示遗忘门。参数W、U、V分别为隐含层、输入层、输出层对应的权值,b为偏差。操作符⊙表示元素级的乘法。σ和tanh分别表示sigmoid和tanh的激活函数,它们是用方程(15)-(16)定义的。

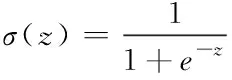
(15)

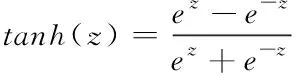
(16)

与LSTM网络结构类似,深度门控循环单元(gated recurrent unit,GRU)相比于LSTM网络内部结构减少了门单元和隐藏状态,并由重置门和更新门取代,内部结构比较简单,但处理大量数据的效果不如LSTM网络[29]。

3 VMD-RL-LSTM风功率预测模型

3.1 模型构建思路

基于VMD-RL-LSTM的短期风功率预测模型如图3所示。主要分为4个步骤。

图3 基于VMD-RL-LSTM的短期风功率预测模型

1)利用VMD方法将原始风功率数据分解,由此获得K个分量。

2)使用中心频率法将分量的个数进行确定,把中心频率值近似的分量确定为相似模态,得到VMD各分量的中心频率。

3)对分解后的分量分别构建LSTM预测模型,然后利用RL学习模块对其输出进行评价,随后反馈给预测系统,对其进行参数调整和优化。

4)将不同分量预测后的结果进行组合叠加,得到一个总的预测输出,并通过误差指标与其方法的比较分析模型的预测性能。

3.2 数据预处理

预测结果的准确性取决于数据集的质量和数量。本文采用选用河北省某风电场实际采集数据,样本的采样周期为5min,选取6月1日-6月8日共2304个点作为样本数据。原始风功率数据如图4所示,其中前2016个点(6月1日-6月7日)的数据作为训练样本,后288个点(6月8日)的数据作为测试样本。

图4 原始风功率数据

3.3 中心频率法确定分量个数

在本文中,K值用中心频率确定,并且将其预设模式编号值K由小到大排列,当最后一层IMF分量的中心频率保持相对稳定时,此时可以考虑K作为最优模式编号值。利用VMD方法分解不同K值的原始风功率序列,获得对应的中心频率,如表1所示。由此可以得到,最后一层分量的中心频率在K>5后保持相对稳定,故最优值为K=6。通过多次反复试验:α=1000;τ=0.3,为确保分解结果的精确度,分解结果如图5所示。

表1 不同K值下各IMF分量中心频率

图5 VMD分解波形

3.4 LSTM网络参数设置

建立LSTM短期风功率预测模型,应考虑样本训练步长、输入层维数、隐含层维数、输出层维数等参数。通过强化学习选择参数寻优,如表2所示。依据实践的经验LSTM层数取L=2,考虑到模型训练的精度准确性和耗时性,时间步长设置为4,输入层维数设置为1,隐含层层数设置为1,隐含层神经元的数量可以设置为200,迭代的次数可以设置为300。初始化的学习速率一般设置在0.01,为了有效防止模型的来回振荡,采用迭代速度衰减法进行动态地调整学习速度,每50次替换迭代地学习速度衰减50%。

表2 LSTM网络参数选择情况

4 分析与讨论

通过VMD-RL-LSTM短期风功率模型的预测,叠加各分量的预测值,将最终预测值与真实值进行比较,如图6所示,该模型的预测值与真实值相吻合,预测精度较高。因此,本文建立的模型可进行短期风功率预测。

图6 模型预测结果

为了验证VMD-RL-LSTM模型的预测性能,本文采用LSTM、EMD-LSTM、VMD-LSTM 3种风功率预测方法进行对比分析,如图7所示。以上预测模型利用均方根误差RMSE、绝对平均误差MAE、平均绝对百分误差MAPE进行评价,模型预测误差对比见表3。

表3 不同模型预测误差

图7 不同模型的预测结果

由表3可以看出, VMD-RL-LSTM模型的预测精度要比其模型更加精确。其均方根误差RMSE、绝对平均误差MAE、平均绝对百分误差MAPE分别为135.10W、0.03%、83.09W,均方根误差RMSE、绝对平均误差MAE、平均绝对百分误差MAPE与单一模型LSTM神经网络相比降低了2997.82W、1.81%、2153.56W;同时相比于EMD-LSTM、VMD-LSTM模型的预测精度有较大提高。说明VMD-RL-LSTM模型可以将短期风功率预测的准确度进行有效提高。

5 结论

本文在风功率序列中采用变分模态分解进行稳定化处理,通过强化学习参数寻优,建立各分量的LSTM预测子模型,最终把各子模型预测的数据进行叠加,从而获得短期风功率预测结果。通过实例分析与讨论,得出以下结论:

1) VMD分解可以将不均匀、随机的风功率序列划分为相对稳定的IMF成分,增加了时间序列的可预测性。

2)在VMD-LSTM神经网络训练过程中采用强化学习算法,并对LSTM网络参数进行寻优,实现了对VMD-LSTM网络模型训练效率的提高,并能有效减轻过拟合现象。

3)VMD-RL-LSTM模型可以将短期风功率进行有效的预测,与其典型短期风功率预测模型比较而言,预测效果更佳。