借助“以形解式”比较两位数乘两位数算式积的大小

文|朱 佳

借助“以形解式”的方式，可以直观地对两位数乘两位数的算式进行积的大小比较，具体过程如下：

一、聚焦本质，建立形与式的联系

1.出示乘法算式5×6，提问：你能画图表示这个式子吗？

2.展示学生作品，引导学生发现可以画长方形来表示这个乘法算式（如图1）。

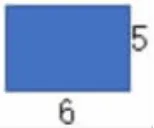
图1

二、初探方法，讨论重叠部分的产生

1.探索类型1：出示25×47○25×49（图2）和25×47○35×25（图3），引导学生从形的角度解释比大小的结果。通过平移旋转重叠，学生发现两个算式之间是包含关系，如果两个算式中有一个因数相同，那么另一个因数大的算式结果就大。

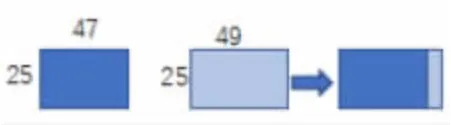
图2

图3

2.探索类型2：出示25×47○35×50（图4），学生通过平移重叠，发现虽然这两个算式没有相同因数，但也是包含关系。两个算式中两个因数都大的算式结果就大。

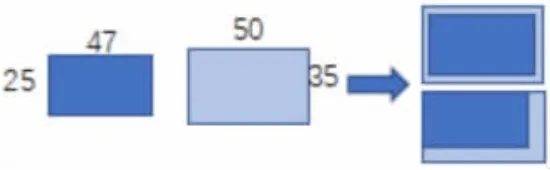
图4

3.对比上述两种类型，发现都是包含关系即都有重叠部分，并引导学生寻找出重叠部分的表示方法即把每个长方形长和宽进行一一对比，挑出较小的长和宽相乘就是重叠部分的表示方法（图5）。

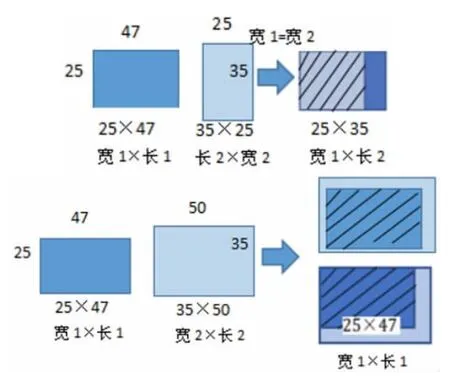
图5

三、深探方法，讨论多余部分的产生

1.探索类型3：出示25×47○35×40，学生发现虽然所有因数都不同，但图形仍有重叠，去掉重叠部分，依然可以比较两个算式的大小。（图6）

图6

2.寻找表示剩余部分①和②算式的方法：先确定重叠部分的算式（方法如图6），然后得出①和②的算式是7×25和10×40，再对这两个算式进行比较。

3.发现：比较两个乘法算式积的大小就是比较剩余部分算式积的大小。

四、综合运用，体会以形解式的优势

1.出示32×48○43×52，99×47○35×47，23×47○57×13。

2.学生尝试用上述方法比大小。

3.交流反馈如何通过“以形解式”方法比较结果。

上述“以形解式”的方式，可以直观地比较两位数乘两位数算式乘积的大小，降低了学生的计算难度，有助于培养学生的画图表征能力、分析能力和推理能力。