基于身高数据的统计规律性分析与概率统计教学研究

摘 要：统计规律性是概率论与数理统计的一个基本定义，对其的探索贯穿于统计研究的始终。本研究通过对某项研究中父母、子女身高的历史真实数据进行科学分析，对统計规律性进行了探索，并结合数据的处理过程强化了对统计规律性的认识，从而做到理论与实践相结合，更好实现了课程教学目标。

关键词：统计规律性；概率统计；身高数据

统计学是研究随机现象统计规律性的一门科学与艺术，该学科不仅要求掌握基本知识和基本理论，还要有统计的思想和艺术。概率论与数理统计（以下简称“概率统计”）作为统计学科的一门基础课程，已成为理工、农医、经济、管理等专业本科阶段的必修课。如何基于概率统计的课程内容，在传授基本知识和基本理论的同时，培养学生的统计思想与艺术能力，使他们具备探索随机现象的统计规律性的综合素养，是统计教育工作者在教学中一直积极探索的内容。

笔者基于R语言包HistData中的父母、子女身高数据，结合数据收集的目的，在对数据进行加工的同时探讨其统计规律性，强化了对概率统计相关概念的认知和应用。

一、数据背景

英国生物学家查尔斯·罗伯特·达尔文（Charles Robert Darwin）于1859年在其著作《物种起源》中提出了生物进化论学说，并将其作为适者生存理论的基础。达尔文的表弟弗朗西斯·高尔顿（Francis Galton）对进化论产生兴趣后，决定对“天赋的遗传”开展研究。受条件所限，他选择了更容易测量的遗传特征——身高。他收集了205个家庭的成员的身高、体重、特定骨骼数据以及其他特征，并将这些数据制成表格反复研究，希望找到一种以父母身高预测子女身高的统计方法。

R语言包HistData中给出了这个调查结果，并将其命名为GaltonFamilies，同时还给出了名为Galton的数据。Galton是GaltonFamilies的简化，只包含“parent”（父母身高）和“child”（子女身高）两个变量。Galton有928个观测值，即来自205个家庭的928个成年子女的身高（单位：英寸，1英寸=2.54厘米）数据。数据中，父母的身高数据为父亲身高和母亲身高的平均值。

要基于Galton数据探讨统计规律性，就需要理解统计规律性的概念。统计规律性是进行大量重复性试验和观测时试验结果呈现出的规律性，如抛掷质地均匀的硬币，出现带币值的一面朝上的次数约占抛掷总次数的一半。《统计大辞典》将统计规律性定义为“大量随机现象在多次重复出现时所呈现的各种规律性”“其主要表现是：在随机现象大量重复出现时，它的每种可能结果出现的频率的稳定性，以及各种数量特征的平均水平的稳定性。如，对一批产品进行还原抽样，各次抽样的结果具有随机性，但是多次重复抽样中不合格产品出现的频率稳定在整批产品的不合格率附近；在分析天平上称量一件物品，各称量的结果具有随机性，但是多次重复称量结果的平均值稳定在被称物品的质量附近……这种稳定性就是统计规律性的典型表现”。从上述定义可以看出，统计规律性是对大量的观测进行有效信息提取的过程，而有效提取信息则要基于实际问题。为此，笔者结合高尔顿收集的Galton数据及收集目标，探讨了Galton数据中隐含的统计规律性。

二、数据的描述性统计规律

描述性统计是指对调查样本中的大量数据资料进行整理、分析和计算，从而得到数据分布特性的概况。描述性统计分析的方法有很多，其中统计图形方法具有直观、形象的特点，可以给出数据的整体分布情况。为此，笔者首先执行R语句命令：

library（HistData）#加载包，如果没有安装，需要运行语句：install.packages（“HistData”）

plot（child～parent，data=Galton，xlab=“父母身高（英寸）”，ylab=“子女身高（英寸）”）#作图

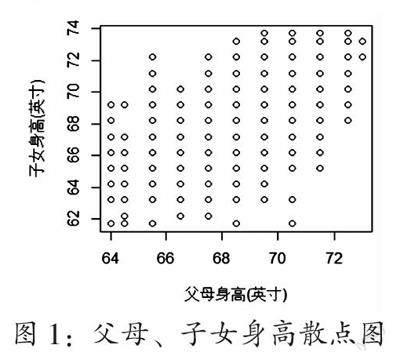
执行命令后得到图1：

图1是以父母身高（parent）为x轴、子女身高（child）为y轴的散点图，可以看出父母身高与子女身高的整体分布情况。观察者可以沿着x轴观测y轴的取值变化，比如父母身高在64英寸附近时，子女身高值有的低于62英寸，有的接近70英寸，这说明有的子女身高比父母低，有的比父母高，但比父母高的子女更多。同样，高个子父母的子女身高也较高，但也有不少子女身高比父母矮。这正如高尔顿和其助手在研究中指出的那样，“高个子的父母更容易拥有高个子的后代，但其子女往往比父母矮，而矮个子的父母其子女往往比父母高”。高尔顿将这种现象形象地称为“均值回归”，这就是图1所给出的Galton数据的统计规律性。

虽然统计图形具有直观、形象的特点，但不同的观察视角往往导致统计图方法产生一定的主观性。因此，可以基于特定的问题或特定的角度，对这些数据进行加工，提取某方面的信息以展示其统计规律性。如要了解19世纪的伦敦居民的平均身高，则可以对Galton数据中的“parent”和“child”变量求均值，运行下面的语句：

apply（Galton，2，mean）#对Galton数据变量求均值

得到父母身高的均值为68.31英寸，子女身高为68.09英寸，子女与父母平均身高相差不大，从而可以认为当地居民的平均身高约为68英寸（172.72cm），这就是当时伦敦居民平均身高的统计规律性。该统计规律性是对来自205个家庭的928名成年子女的身高数据进行平均而得到的，所以68英寸这个身高值有可能比实际值高或低，这取决于样本是否具有代表性。如果样本具有良好的代表性，那么这个值就能够反映当时伦敦居民的平均身高情况，这就是统计规律性。

若要了解当时伦敦居民身高的差异情况，则可以计算身高数据的方差（标准差）。方差（标准差）越大，说明居民之间身高的差别越大，反之则越小。运行下面语句：

apply（Galton，2，var）#对Galton数据变量求方差

apply（Galton，2，sd）#對Galton数据变量求标准差

得到父母、子女身高的样本方差分别为3.19和6.34，父母、子女身高的标准差分别为1.79和2.52。基于正态分布的“3σ”法则，区间（60.53， 75.65）（=（68.09-3×2.52，68.09+3×2.52））应以0.9973的概率包含伦敦居民的身高。对于Galton数据，父母、子女身高的最大值分别为73和73.7（运行代码：apply（Galton，2，max）），最小值分别为64和61.7（运行代码：apply（Galton，2，min）），均落在“3σ”区间内。由此可见，均值、方差、标准差以及“3σ”区间等值，均从不同角度展示了Galton数据的统计规律性。

上述结论中，子女身高的方差（标准差）比父母身高的方差（标准差）大，说明子女身高的离散程度大，这在数据中也有所体现——子女身高的最小值61.7比父母身高的最小值64小，而最大值73.7比父母的73大。但这个结论似乎与高尔顿“均值回归”相矛盾，这种假象的产生与样本的采集有关：一是因为父母的身高是父亲与母亲身高的平均值；二是因为928名成年子女来自205个家庭，父母身高的数据也只有205个不同的值。以上两个因素导致了父母身高方差变小，这也是Galton数据的统计规律性所在。

三、数据的推断统计规律

高尔顿采集数据的目的是想找到一个统计模型，在已知父母身高的条件下预测其子女的身高。概率统计课程中的回归分析是一个常用的统计预测工具，那么回归分析又是如何体现统计规律性的呢？

首先，基于R软件包stats中的lm函数，运行语句

galton.lm=lm（child～parent，data=Galton）#建立父母身高对子女身高的线性回归模型

summary（galton.lm）

由summary（galton.lm）输出，给出的回归模型为：子女身高=23.94+0.65×父母身高。（1）

模型（1）将928名子女和205个父母的身高数据统计提取为两个数值：截距项23.94和斜率0.65。显然，父母身高对子女身高具有正向作用，因为斜率0.65为正值，但0.65<1，说明父母身高对子女身高的影响并不是1∶1的。在父母身高已知的条件下，基于模型（1）可以给出子女身高的预测。比如父母身高是68英寸，代入模型（1）给出子女身高为68.14英寸，基本与父母身高持平；如果父母身高为62英寸，则子女身高64.24英寸，有增高的趋势；如果父母身高为75英寸，则子女身高为72.69英寸，有降低的趋势。这就是高尔顿给出的“均值回归”现象，而截距项23.94和斜率0.65就是Galton数据的线性回归模型的统计规律性。

笔者基于Galton数据，从统计图、均值、方差和“3σ”区间等角度给出了统计规律性的描述性分析，有助于加深学生对统计规律性的认识，帮助他们进一步理解统计推断的统计规律性。

参考文献：

[1]袁卫，刘超.统计学教材建设的问题与思考[J].统计研究，2011（9）.

[2]（美）L·迪·芬克.创造有意义的学习经历：综合性大学课程设计原则[M].胡美馨，刘颖，译.杭州：浙江大学出版社，2006.

[3]常艳芳.让学生获得有意义的学习经历：现代大学教育的承诺[J].江苏高教，2019（1）.

[4]王秀芝.案例教学中需要研究的几个问题[J].中国高等教育，2006（12）.

[5]（美）戴维·萨尔斯伯格著.女士品茶：统计学如何变革了科学和生活[M].刘清山，译.南昌：江西人民出版社，2016.

[6]王松桂，张忠占，程维虎，等.概率论与数理统计[M].北京：科学出版社，2011.

[7]郑家亨.统计大辞典[M].北京：中国统计出版社，1995.

责编：文 墨

基金项目：河南工业大学首批特色课程（编号：PX-41211821）

作者简介：郭念国（1976— ），男，河南工业大学副教授，研究方向为应用数理统计。