解构概念教学 关注素养发展
黄贤明 袁琴琴

【摘 要】数学核心素养的研究是数学教育界关注的重点。文章以“绝对值与相反数”为例,通过同课异构的方式从关键能力、基本思想与数学品格三个维度对比两位一线教师的概念教学,并基于发展核心素养的角度提出了对绝对值的教学思考。
【关键词】绝对值;概念教学;同课异构;数学核心素养
【作者简介】黄贤明,二级教师,主要研究方向为初中数学教学研究;袁琴琴,一级教师,主要研究方向为初中数学教学研究。
一、引言
核心素养是当今教育界关注的重点,它是学生应具备的,能够适应终身发展和社会发展需要的必备品格和关键能力,也是落实立德树人根本任务的坚实向导。随着《义务教育数学课程标准(2022年版)》的颁布,明确了数学核心素养三大构成,即“会用数学的眼光观察现实世界”“会用数学的思维思考现实世界”“会用数学的语言表达现实世界”(简称“三会”),在初中阶段主要表现为抽象能力、运算能力等九大能力[1]。数学概念是涵养数学思想、培育核心素养、渗透数学文化的重要载体,在数学教育中发挥着不可替代的作用。从数学教育心理学的角度看,数学概念的学习是通过对现实情境的抽象与归纳,同化或形成概念意象,而后将其进行知觉水平的应用,经历概念的多种表征,形成概念系,建立概念图示,最终达到对概念的思维水平层面的应用[2]。通过对“绝对值与相反数”同课异构活动的研究发现,教师C和教师Y的课堂教学各有特色,但也存在一些值得斟酌之处。本文从两位教师的课堂出发,思考如何在绝对值概念的教学中落实数学核心素养,并提出教学思考,以期为绝对值教学提供参考。
二、素养导向下的课例评析
(一)宏观比较
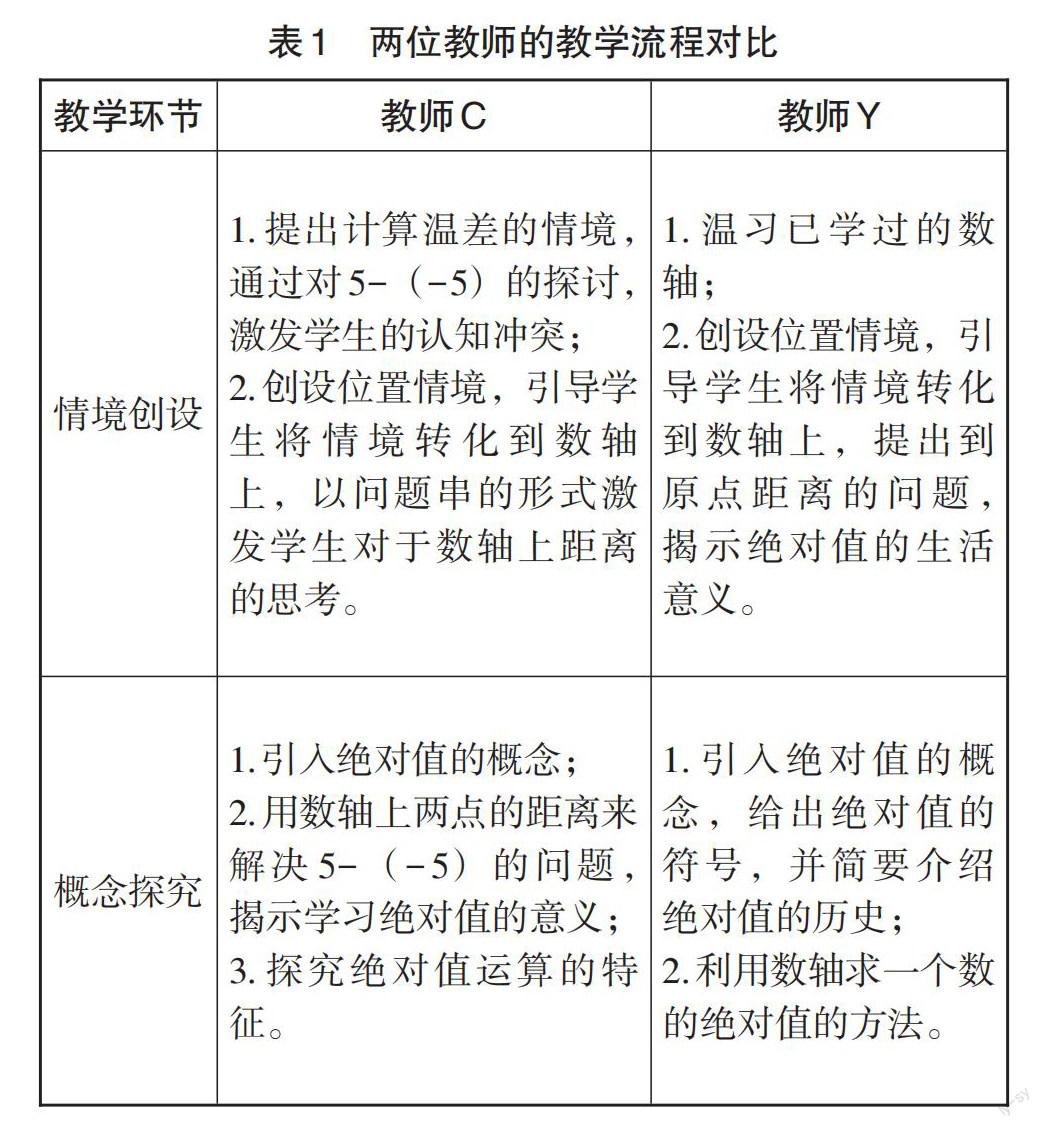
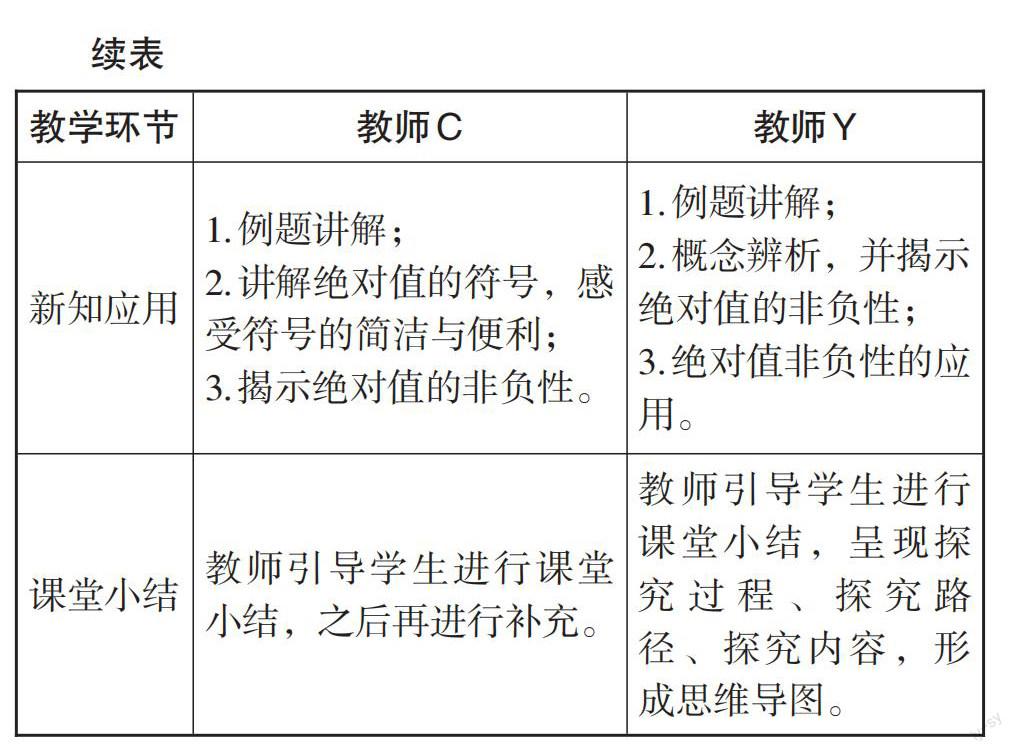
从宏观上看,本节课的教学过程设定为四个环节,教师C和教师Y具体的教学流程见表1。
由表1可知,教师C和教师Y都重视创设情境的教学价值,旨在以同化的方式生成绝对值的概念,揭示绝对值的生活意义。对绝对值的引入,教师C以温差问题的探讨指出学生目前所未知的问题,为数轴、距离等概念的引出提供情感基础,之后从对距离情境的抽象与探索中自然生成绝对值的概念。而教师Y直接从复习数轴的角度,激活学生的原有经验,并以距离情境直观揭示绝对值的内涵。对于绝对值概念的探究,教师C通过对5-(-5)的再次探究,而教师Y则基于数轴探索绝对值的求法,立足学生“四基”的发展。在绝对值的应用环节,两位教师都使用了教材中的例题,但教师C借助例题阐述了绝对值符号的价值,而教师Y则呈现了绝对值非负性的应用,让思维更有深度。
(二)微观比较
核心素养是具有数学基本特征的关键能力、思维品质以及情感、态度与价值观的综合体现。笔者在下文从关键能力、基本思想与数学品格三个维度对两节课进行微观比较。
1.关键能力的培养
关键能力的培养是发展数学核心素养的根本,其可概括为“三会”,在初中阶段具体表现在抽象能力、运算能力等九大能力。关键能力的培养是需要课程为支撑,教学为载体,并在教师有计划、有目的的教学实践中循序渐进的发展。在概念课中,关键能力的培养着重体现在抽象能力之中。
数学知识的获得是人们对于现实世界的观察与抽象,现实世界也是数学知识的重要载体。对于绝对值的引入,两位教师都从现实情境出发,选择了类似的距离情境。教师C设计了“老师家在学校正西方向5 km处,小明家在学校正東方向5 km处”的情境,教师Y设计了“汽车司机从车站出发,沿东西方向行驶,若向东行驶3千米到加油站,若向西行驶2千米到超市”的情境。以上两个情境都贴近学生的现实生活,并且立足于学生近期所学习的数轴、正负数等知识,有利于学生自发地用数学的眼光抽象出现实情境中的数轴模型,形成绝对值概念的基本雏形,指向学生抽象能力的培养。
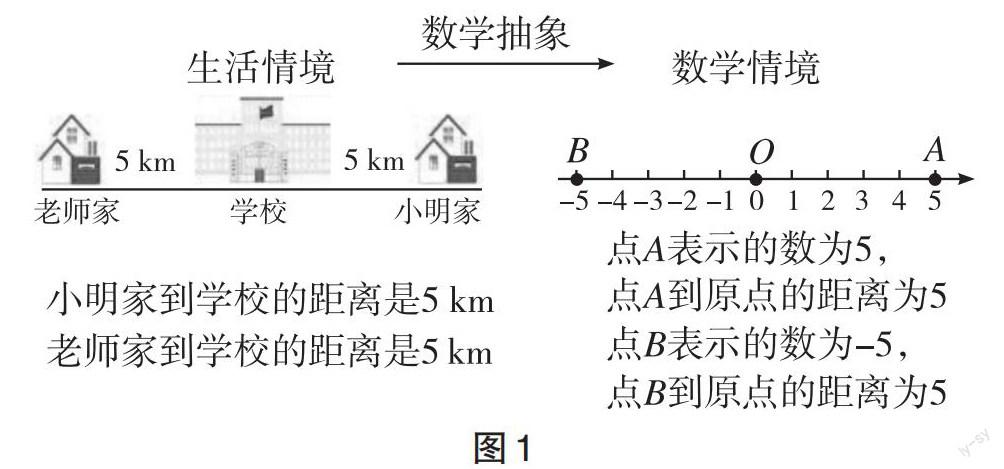
由于绝对值概念的特殊性,教学中往往需要教师建立起距离与绝对值的联系,促进学生理解绝对值的几何定义。在概念的抽象概括环节,两位教师都关注到距离对绝对值的意义,但都略有欠缺。其中教师C提出了“老师与小明的到校的时间与哪个量有关?”,以期将学生引到数轴上对到原点距离的思考,但问题中忽视了对速度的考虑。笔者建议教师把握情境中的两个“5 km”,重新设计问题(如图1),引导学生在用数轴表示情境的过程中,自主发现情境中的位置关系(老师家与小明家到学校距离相等)与数轴上“形”的联系(-5与5到原点的距离相等)。之后,教师再加以点拨,让学生发现并归纳两个点的共同特征,进而充分发挥该情境的价值,构建绝对值的现实意义,间接地培养学生的抽象概括能力。
教师Y则直接将加油站(表示的数为3的点)和超市(表示的数为-2的点)到车站(原点)的距离构建意义,给出绝对值的概念与符号。以上教学设计看似简洁明了,实则忽视了学生对事物感知识别、分类概括的过程,略有“伪发现”之意。数学抽象的发展依次经历简约阶段、符号阶段与普适阶段,在简约阶段中需要重点围绕实物抽象,清晰地了解事物的本质特征,而后才进入符号阶段,用数学语言简化概括的一类事物[3]。截止符号的给出,课堂才进行不到十分钟,学生对于绝对值概念理解不深刻,未完全建立绝对值与距离的联系,也未让学生感受到绝对值的意义与绝对值符号的价值。因此,笔者建议教师再多呈现数轴上的几个位置,让学生说一说这些位置到车站(原点)的距离,进一步思考它们的共同属性(都是到原点的距离),并在教师的引导下归纳总结出绝对值的几何定义。只有这样学生才切实经历概念抽象的完整过程,才能有利于学生数学抽象活动经验的积累与数学核心素养的发展。当然,绝对值的符号也不建议过早给出,要在学生内化理解了绝对值的几何意义之后再呈现,从而彰显符号的独特价值。
2.基本思想的形成
数学学习不仅包括数学知识的习得,还包括知识的形成过程和蕴含的数学思想方法。基本思想的形成是数学教学的过程性目标,体现在与学生参与的课堂活动之中,包括数学思想、数学方法、数学思维等。两位教师的课堂都关注到基本思想的培养,尤其是将数形结合思想串联到绝对值的探究环节。
两位教师的课堂中,都对现实情境的抽象并获得了数轴的模型,通过对数轴上点与原点的距离的思考,将绝对值的引出与距离建立现实意义,实现“以数助形”。在课堂练习环节,两位教师都选择呈现直观的数轴,引导学生借助距离来解决“求一个数绝对值”的问题,实现“以形解数”。教师Y的课堂中,呈现了思维导图(如图2),归纳出求绝对值的方法,促进学生将具体的数轴转化为抽象的数轴,使绝对值与数轴的关系达到“数形交融”的境界。
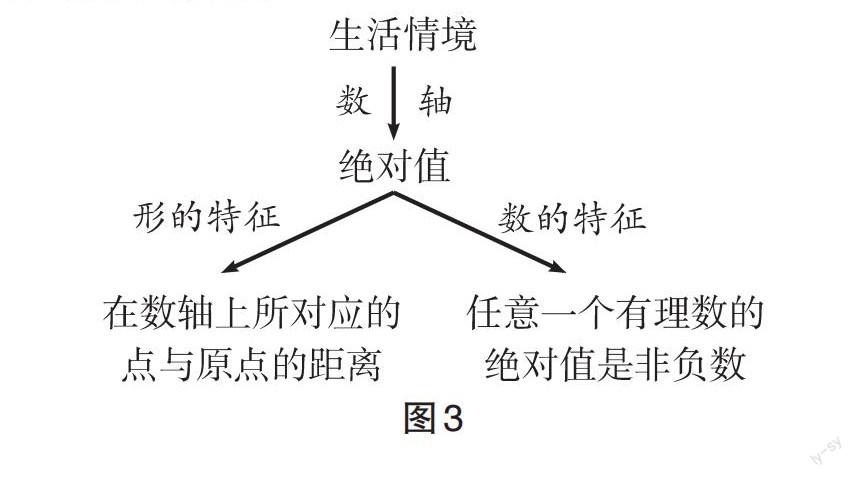
此外,在课堂小结环节,教师Y的课堂充分彰显了结构化的特征,重视绝对值探究过程的总结。如图3,教师Y从探究过程、探究路径、探究内容等角度形成了知识的逻辑与框架,促进绝对值以知识体系的形式纳入学生的认知结构,积累概念探究的活动经验。但美中不足的是没有给学生一种“回味无穷”之感,即没有关注到概念的发展流程、前后知识的逻辑关系与知识背后的文化,忽视了课堂小结的启下作用。
最后值得指出的是,两位教师都忽视了教学的开放性,即通过开放的问题与活动,构建开放的课堂,促进学生形成开放的思维。例如,在绝对值符号给出的环节,能否让学生先发挥创意创造一个符号,培养学生的创新意识;在求绝对值环节,能否让学生相互出题、回答、说明理由,提升学生数学交流能力等。
3.数学品格的发展
数学品格属于数学核心素养的一部分,比数学思想等拥有更高的价值追求,是数学教育的原点。数学品格包括文化性品格和工具性品格,两者共同构建数学学科的育人价值。数学品格的组成要素主要涉及数学兴趣、创新、自强不息、严谨性、勇于质疑、化繁就简和独立思考[4]。数学品格虽然价值高,但在教学中常被忽视,处于“高评价、低应用”的状态。数学品格的培养作为数学教学更高层次的目标,需要教师有意识的、连续的在课堂教学中让学生潜移默化地形成与发展。
在课堂导入环节,教师C从今日的气温出发,提出计算温差的问题,之后将气温变为-5℃~5℃,再次设问如何求温差。此设计从现实世界的问题出发,旨在引导学生通过数学的眼光观察现实世界,并通过两个问题将学生从已有引入未知,激发学生的探究兴趣与探索欲望,发挥着“启旧引新、设疑激趣”的作用,同时也暗含着绝对值数学意义的构建,为课堂埋下伏笔。针对绝对值符号的学习,教师Y也给出了绝对值符号的相关历史,简单介绍了绝对值符号的起源与含义,拓宽学生视野,促进学生文化性理解的形成。
精彩在始,精致于终。课堂小结应发挥承上启下、巩固自评、构建体系等作用,而两位教师在课堂小结环节都忽视了情感层面的小结。如教师C以“在本节课中,你印象比较深刻的内容是什么?”结束,并让学生总结回答。看似学生是主角,实则是走过场,既没有体现非概念性知识(如探究过程、思想方法等)的总结,又匆忙地结束课堂,使得课堂小结“名存实亡”。
三、数学核心素养视角下对概念教学的思考
(一)明晰概念的探究过程,关注素养的有效发展
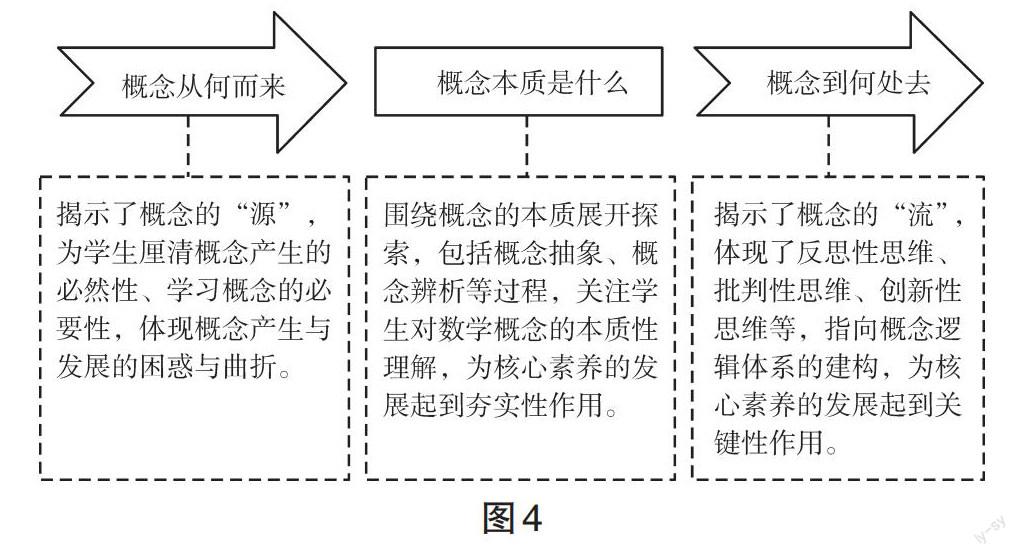
概念的获得并不是一蹴而就的,是学生在多种刺激与反应的共同作用下发生的,其关键在于促使学生建立新旧知识的内在联结,形成对概念的本质性理解。在传统教学中,概念的教学往往停留于让学生接受前人创造的知识,最终导致学生知其然而不知其所以然的现状。在素养导向下的概念教学要摒弃结果导向的价值取向,需要将概念发展的逻辑脉络与教学过程相互交融、相得益彰,促使学生在获得并掌握概念的同时经历“概念从何而来”“概念本质是什么”“概念到何处去”的完整探究过程(如图4)。
“概念从何而来”阶段揭示了概念的“源”,为学生厘清了概念产生的必然性、学习概念的必要性,体现概念产生与发展的困惑与曲折。正如两位教师的课堂都以距离情境揭示绝对值的生活意义,带领学生感知绝对值存在的客观性与必然性,其中教师C以一种大观念的视角指明了绝对值为后续有理数运算学习的意义,通过这些方式为学生的思维提供了更大的活动空间。在“概念本质是什么”环节,教师需立足概念的本质,关注概念的探究过程。因而绝对值概念教学要借助数轴的“形”,围绕绝对值的几何意义的构建展开,即教师在情境中让学生以数学的眼光、语言获得对绝对值本质属性的理解,并可以像教师Y一样设计概念辨析环节,促进学生在正反例的比较辨析中强化概念的认识,为发展学生的数学核心素养起着夯实性作用。在“概念到何处去”的环节,教师要做到“有中生新”,引导学生总结概念探究中的思想方法,积累数学活动经验;揭示概念的应用背景,提升数学应用意识;感悟概念发展逻辑,形成概念知识体系。在此环节中,学生的反思性思维、批判性思维、创新性思维等都得以激活,在数学核心素养中起到了关键性作用。
(二)立足概念的本质内涵,促进素养的整体形成
在素养导向下的概念教学中,核心素养以关键能力、基本思想与数学品格这三种形式渗透于概念教学的始终。因此,教师需要先审视概念的本质内涵,挖掘其所蕴含的核心素养,明确素养导向的教学目标。例如,绝对值概念的本质在于建立其与数轴上的点到原点距离的联系,围绕这一本质所蕴含的核心素养就具体体现在抽象能力、几何直观的关键能力与数形结合的基本思想。之后,教师在此基础上构建概念教学框架,设计教学方法,实施教学活动,以实现核心素養的教学融合。
此外,教学不仅要立足概念的本质内涵,还要强调表达概念的抽象结构,即关注以概念为中心所统摄的新内容,如:概念的性质、关系、运算等[5]。正如教师C将绝对值与有理数的加减运算的思想融为一体,更有利于突出绝对值概念的本质,凸显绝对值的学习价值,促进学生数学核心素养的形成与发展。当然,教师在教学中不仅要重视知识技能的传授,还要关注数学品格的形成。在概念教学中,教师可以尝试创设贴近学生实际生活的情境,设计探究性问题链,组织多样化的数学活动,呈现生动有趣的历史素材,促使学生形成对概念学习的积极心理,实现素养的整体性发展。
最后需要指出的是,学生核心素养的培养并不是急于求成、一蹴而就的,也不是靠“喊口号”“拉横幅”就能达成的,教师需要认识到核心素养发展的连续性、阶段性、整体性等特征,在一定的理论和实践的引领下,有意识、有目的地将核心素养的培养渗透于数学教学中,促进学生在坚实的“四基”与“四能”下习得数学思维方式、发展数学关键能力、形成良好的数学品格与健全人格,最终落实立德树人的根本任务。
参考文献:
[1]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.
[2]喻平.数学教学心理学[M].2版.北京:北京师范大学出版社,2018.
[3]史宁中.数学思想概论(第1辑):数量与数量关系的抽象[M].长春:东北师范大学出版社,2008.
[4]祖丹,孔凡哲.数学必备品格的组成要素分析:基于数学家的视角[J].天津师范大学学报(基础教育版),2020(2):59-65.
[5]史宁中.《义务教育数学课程标准(2022年版)》的修订与核心素养[J].教师教育学报,2022(3):92-96.
(责任编辑:陆顺演)

