差分码偏差对QZSS 单点定位的影响

李佳豪，贾小林，杜彦君，徐煜

(1.长安大学地质工程与测绘学院,西安 710061；2.西安测绘研究所,西安 710054；3.西安科技大学测绘科学与技术学院,西安 710054)

0 引言

准天顶卫星系统(QZSS)是由日本宇宙航空开发机构(JAXA)研发和实施的区域导航系统[1].自2018年来，QZSS 已有4 颗可用卫星，其中包括1 颗地球静止轨道(GEO)卫星和3 颗倾斜地球同步轨道(IGSO)卫星，共发射L1(1 575.42 MHz)、L2(1 227.60 MHz)和L5(1 176.45 MHz)三种频率信号，能为亚太地区提供基本定位、导航和授时(PNT)服务[2].据日本内阁府宣称，QZSS 系统将分为两步完成：第一步于2018年组成4 颗卫星提供正式服务；第二步计划于2023 年再发射3 颗卫星，届时将由7 颗卫星组成完整星座.未来，QZSS 系统将在GNSS 中发挥重要作用[3].

差分码偏差(DCB)是不同类型的测距码在卫星和接收机内部传输过程中产生的时延偏差，是提取高精度电离层延迟和卫星精密定位中不可忽略的一项系统性偏差，因此建立DCB 改正模型对高精度定位有重要意义[4].目前已有不少学者对卫星端DCB 改正进行了分析，Guo 等[5]阐明了北斗卫星导航系统(BDS)DCB 与时间群延迟(TGD)参数之间的关系，同时证明两者改正模型的等价性，并通过实验分析得到高精度定位必须采用DCB 或TGD 改正的结论.王宁波等[6]分析了GPS 民用广播星历中信号间校正(ISC)参数精度以及对定位精度的影响，实验表明经ISC 参数改正后，GPS 单、双频伪距单点定位(SPP)精度都有明显提升.袁海军等[7]推导了北斗三号(BDS-3)新频点单、双频SPP 和双频精密单点定位(PPP)的DCB 改正模型，结果表明经DCB 改正后，单、双频SPP 定位精度分别提升了48%～85%和71%～91%，静态双频PPP 的收敛时间提高了56%～83%.

目前，QZSS 可与其他导航卫星系统兼容，在一定程度上改善了亚太地区定位的可靠性、可用性和定位精度.Li 等[8]比较了单QZSS、GPS 和GPS/QZSS在不同截止高度角下的定位精度分析，发现QZSS/GPS组合较单系统的可见星数明显增加，位置精度因子(PDOP)值降低，定位精度更高.随着QZSS 的不断建设，研究其单点定位精度对QZSS 的应用以及后续的发展具有重要意义，且QZSS 广播星历钟差参数基准为L1/L2 无电离层组合(IF)，在使用不同于钟差参数基准的观测值时需引入相应的TGD或DCB 改正.基于上述讨论，本文分别推导了L1、L2 单频和L1/L2双频SPP TGD 和DCB 改正模型，采用多模GNSS实验工程MGEX(Multi-GNSSExperiment)跟踪站数据进行实验，分析了TGD 和DCB 改正对QZSSSPP定位的影响.

1 观测方程及TGD/DCB 改正模型

1.1 伪距观测方程

原始伪距观测方程可以表示为

SPP 双频组合通常采用消除一阶电离层延迟的IF 组合模型，对式(1)进行IF 组合后的伪距观测值为

1.2 QZSS 的TGD 改正公式

在进行单点定位时，接收机DCB 可被接收机钟差吸收后作为待估参数解算，而卫星DCB 须予以改正[9].目前，QZSS 的广播星历钟差是以L1/L2 双频IF 组合作为基准，其广播星历钟差可以表示为

因广播星历的基准为L1/L2 无电离层，在进行L1/L2 组合时双频组合模型无需进行TGD 或DCB改正.

1.3 QZSS 的DCB 改正公式

目前MGEX 发布DCB 产品的机构主要有中国科学院(CAS)和德国宇航中心(DLR)，且CAS 和DLR 发布的DCB 产品都具有较高的稳定度[10-11].本文采用CAS 发布的DCB 产品，其具体定义为

将式(7)带入式(4)可推导出SPP 单频L1 和L2频点卫星端DCB 改正模型，如式(8)所示[5]：

2 实验与分析

2.1 数据来源及处理方案

为了分析卫星端DCB 改正对QZSS 单、双频SPP 定位精度的影响，本文选取亚太地区6 个MGEX测站2022 年4 月24 日至2022 年4 月30 日(年积日为114～120)连续7 d 的观测数据进行SPP 定位实验.所有测站均可以接收L1 和L2 频点数据，测站分布位置如图1 所示.卫星轨道和钟差采用国际GNSS服务组织(IGS)提供的广播星历文件，包含TGD 参数，DCB 改正参数来自CAS 发布的BSX 文件，坐标真值取自IGS 提供的SNX 文件，截止高度角为7°，采样间隔为30 s，单频SPP 电离层延迟采用Klobuchar模型修正，双频SPP 采用IF 组合，对流层延迟采用Saastamoinen 模型.

图1 测站分布

本节首先对DCB 的月稳定性以及TGD 和DCB 的符合程度进行分析，统计6 个MGEX 测站7 d 的平均可见星数和PDOP，并分析SPP 历元解算率，最终按照两种处理方案进行SPP 定位精度的分析.方案1，对L1、L2 单频和L1/L2 双频进行SPP 解算，解算过程均不加入TGD 和DCB 改正；方案2，对方案1 中均加入TGD 和DCB 改正，其余策略均相同.在获得解算结果后与真值作差并计算其均方根误差(RMSE)，特别需要说明的是，本文在统计结果时将RMSE 大于20 m 的历元视为粗差剔除[12].

2.2 DCB 稳定性和TGD 符合程度

为探究QZSSDCB 的月稳定性以及DCB 和TGD的符合程度，选取2022 年4 月1 日至2022 年4 月30 日(年积日91～120)连续30 d 由CAS 发布的BSX文件数据进行分析.图2 为QZSS 各卫星DCBC1X-C2X的月时间序列，因QZSS 广播星历中的TGD 参数与CAS 发布的DCB 参数定义不同，将TGD 参数统一到DCB 参数定义上计算出 ISCL2C，图3 为2022 年4 月30 日年积日第120 天的DCB 和TGD 差值.

图2 QZSS 卫星DCB 时间序列

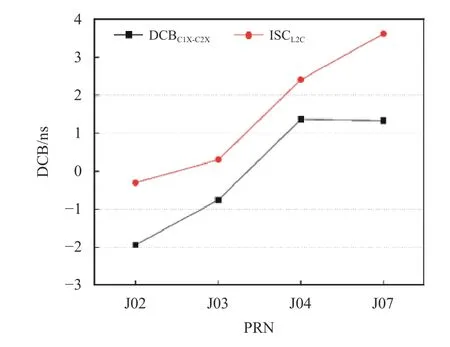
图3 QZSS 单天解各卫星DCB、TGD 及其互差值

从图2 可知，DCBC1X-C2X的日解值范围为-2.06～1.54 ns，各卫星的DCB 月稳定程度较好，无明显大幅度波动，其中J04 卫星的稳定性最高，波动范围为-1.46～1.07 ns，标准差(STD)为0.1 ns，J07 卫星的稳定程度最差，波动范围为0.88～1.54 ns，STD 为0.16 ns.从图3 可知，各卫星TGD 与DCB 的符合程度优于2.5 ns，其中J07 卫星的差值最大为2.29 ns，其次是J02 卫星为1.64 ns，J03 和J04 卫星相当，分别为1.06 ns 和1.05 ns，其余天均有类似的结果.

2.3 可见星数、PDOP 和历元解算率

历元解算率是指SPP 解算成功历元个数占预期历元个数(测站数乘以天数乘以单天历元个数)的百分比，而可见星数和PDOP 值为所有24 h 解的公共时段数据来计算平均值，做图时剔除PDOP 值大于30 的历元.图4 为所有测站7 d 的平均可见星数和PDOP 值以及历元解算率图.表1 为服务时段内各测站7 d 的可见星数和PDOP 均值.

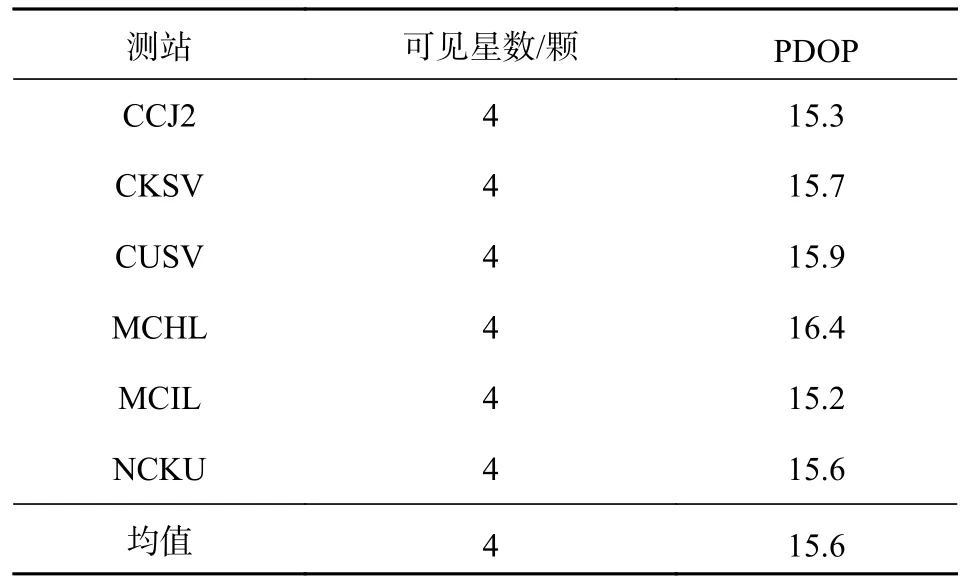
表1 QZSS 服务时段内的可见星数及PDOP

图4 可见星数、PDOP 和历元解算率

从图4 和表1 可以看出：在QZSS 服务时段内6 个测站7 d 的平均可见星数均为4 颗；PDOP 值随历元呈周期性变化，其平均值为15.6，并分别在400、800、1200、1650、2300 历元处出现断点，其原因为对应时段卫星的空间几何构型较差，而第5 个断点的历元缺失个数最多约为1.5 h，其余均约为0.5 h，由此也可得出QZSS 在其服务区内的服务率为79%，这与文献[8]得到的结果相似.从解算率中可得到6 个时段的平均解算率分别为79.5%、73.8%、63.8%、72.7%、80.8%、79.6%，在14:00—19:00 QZSS 的服务时间最长且平均SPP 可用率最高为80.8%，7:00—9:30 QZSS的服务时间最短且平均SPP 可用率最低为63.8%.

2.4 SPP 定位精度分析

按照方案1 和方案2 进行单、双频解算后，图5为具有代表性的2022 年4 月30 日MCHL 测站的L1、L2 单频和L1/L2 双频SPPTGD/DCB 改正前后的定位误差序列图，表1 统计了所有测站7 d L1、L2 和L1/L2 组合频点TGD/DCB 改正前后的平均定位偏差.

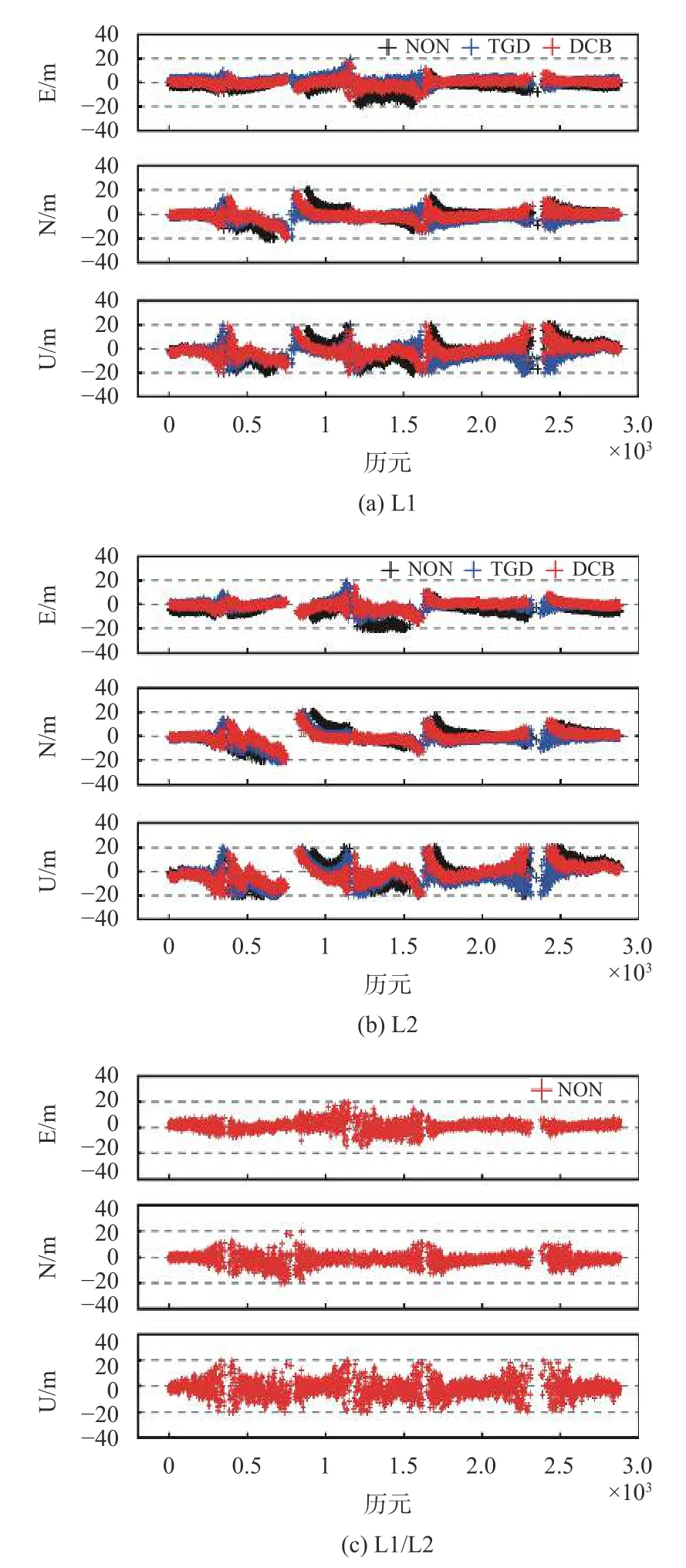
图5 MCHL 测站SPP 定位偏差

从图5 可知，经TGD/DCB 改正后各频点及其组合频点定位误差时序更加平缓，相对于单频而言，双频组合的定位误差时序波动更小，图中出现的5 处断点与上述PDOP 值图类似，其原因为卫星空间几何构型较差.

从表2 可知，TGD/DCB 改正对SPP 的影响均为米级，且DCB 改正较TGD 改正的定位精度略高，改正前L1 和L2 频点在东(E)和天顶(U)方向上定位精度相当、北(N)方向精度最好，改正后N 方向优于E 方向、U 方向最差.提升率方面，TGD/DCB 改正后E 方向提升最大，其次为U 方向，N 方向最小.

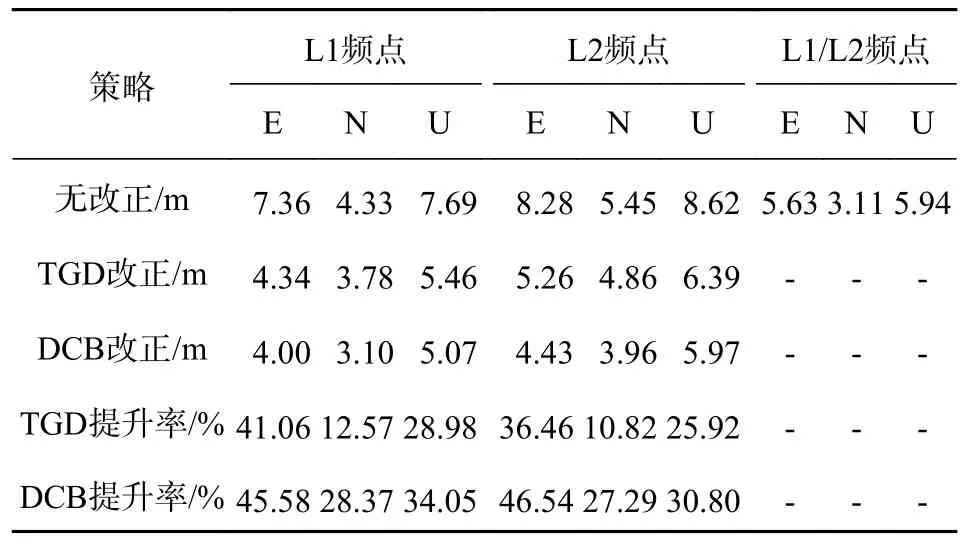
表2 SPP TGD/DCB 改正前后定位精度

改正前L1 频点在E、N 和U 方向上的定位精度均优于L2，L1 和L2 频点定位精度分别为7.36 m、4.33 m 和7.69 m，8.28 m、5.45 m 和8.62 m.经TGD改正后L1 频点的定位精度在各方向上均优于L2，其L1 频点在E、N 和U 方向上的定位精度分别为4.34 m、3.78 m 和5.46 m，提升率分别为41.06%、12.57%和28.98%，L2 频点在E、N 和U 方向上的定位精度分别为5.26 m、4.86 m 和6.39 m，提升率分别为36.46%、10.82%和25.92%.经DCB 改正后L1 频点的定位精度在各方向上仍优于L2，其L1 频点在E、N 和U 方向上的定位精度分别为4.00 m、3.10 m和5.07 m，提升率分别为45.58%、28.37%和34.05%，L2 频点在E、N 和U 方向上的定位精度分别为4.43m、3.96 m 和5.97 m，提升率分别为46.54%、27.29%和30.80%.L1/L2双频组合定位精度优于改正前的单频，而较TGD/DCB 改正后的单频而言，其E 和U 方向定位精度较差且两者精度相当分别为5.63 m 和5.94 m，N 方向上的定位精度优于TGD/BCD 改正后的单频，其值为3.11 m.

整体而言，经TGD/DCB 改正后L1、L2 和L1/L2 SPP 在水平方向的定位精度可从4～9 m 提升至3～6 m，高程方向可从7～9m 提升至5～7 m，提升率为10%～46%.由此可见DCB 对定位精度影响很大，在进行定位解算时需予以改正.

3 结论

为探究DCB 对QZSS 定位精度的影响，本文选取了2022 年4 月24 日至2022 年4 月30 日6 个MGEX测站数据按照两种不同的方案进行实验，得到以下结论：

1)选取2022 年4 月连续30 d DCB 产品数据，对DCB 的月稳定性及TGD 的符合程度进行分析，其中DCBC1X-C2X的日解值范围为-2.06～1.54 ns，各卫星的月稳定程度较好，无明显大幅度波动，卫星TGD 与DCB 的互差值优于2.5 ns.

2)在服务时段内各测站7 d 的平均可见星数为4，PDOP 值随历元呈周期性变化，并存在5 个不同程度的断点，且第5 个断点历元缺失个数最多时长约为1.5 h，而SPP 可用率随PDOP 值成反比，在服务时段内14:00—19:00 QZSS 的服务时间最长且平均SPP可用率最高为80.8%，在7:00—9:30 服务时间最短且平均SPP 可用率最低为63.8%.

3)经TGD/DCB 改正后SPP 的定位精度有较为明显的提升，影响程度为米级，而DCB 改正略优于TGD 改正，且E 方向提升率明显优于U 方向，N 方向提升最小，改正前后L1 频点的定位精度均优于L2.经TGD/DCB 改正后SPP 在水平方向的定位精度可从4～9 m 提升至3～6 m，高程方向可从7～9 m 提升至5～7 m，提升率为10%～46%.因此伪距硬件延迟偏差对SPP 定位有较大影响，在定位过程中不可忽略.

致谢：感谢IGS 提供数据支持.