BDS-3 PPP/INS 紧组合定位性能分析

宋德彪，孙付平，肖凯，柯晔,2，商向永,3，于圆

(1.中国人民解放军战略支援部队信息工程大学 地理空间信息学院,郑州 450001；2.31618 部队,福州 350000；3.光电对抗测试评估技术重点实验室,河南 洛阳 471000；4.32021 部队,北京 100000)

0 引言

高精度定位是精确获取地理空间信息的关键技术，已成为车载移动测绘、航空摄影测量等移动测量领域的迫切需要.差分全球卫星导航系统(DGNSS)与惯性导航系统(INS)的组合定位技术是目前高精度定位手段，但受到基准站及基线长度限制，无法满足远海、高空等领域的移动测量任务，而精密单点定位(PPP)技术可以弥补其缺点.因此PPP/INS 精密定位定姿技术的研究具有重要应用意义.

文献[1]较早对GPSPPP/INS 进行实验研究，结果证明与DGNSS/INS 定位精度相当，均达到10 cm.文献[2]实现了PPP/INS 松组合算法，并验证了松组合并不会提高PPP 定位精度.文献[3]对低成本PPP/INS 算法的松组合、紧组合分别展开研究，实验结果表明，定位精度可以达到分米级.文献[4]在低成本PPP/INS 算法上针对单频信号展开研究.文献[5]对GPS PPP/INS 松组合与紧组合进行了全面的对比，并研究了卫星信号中断及惯性设备对定位结果的影响，实验表明：紧组合定位精度优于松组合，并且紧组合可以加速PPP 收敛.文献[6]验证了多系统可以有效提升PPP/INS 紧组合定位系统定位性能并缩短收敛时间.文献[7]通过实验证明PPP/INS 松组合的定位精度为分米级，速度精度为cm/s 级.PPP/INS紧组合定位性能得到明显改善，定位精度为厘米级，速度精度为cm/s 级.文献[8]利用整数相位钟法首次实现了模糊度固定解PPP/INS 紧组合，经过实验验证，可以实现10 min 模糊度初始固定，定位精度仍然可达厘米级.文献[9]区别于文献[8]，利用小数偏差法实现了PPP/INS 紧组合方案，并引入抗差因子降低海洋环境下的多径效应，经海洋实验验证得到INS可以缩短PPP 重新收敛时间及定位精度达到毫米级.还有其他学者针对PPP/INS 紧组合技术的复杂环境下的粗差及周跳问题展开研究[10-13].

北斗三号全球卫星导航系统(BDS-3)于2020 年7 月31 日正式开通，在2022 年迎来了全球服务的新时代，服务功能及定位性能得到进一步提升[14].BDS-3 PPP/INS 紧组合技术成为当研究的热点.目前BDS-3 PPP/INS 紧组合技术研究还不够全面深入，本文详细推导BDS-3 PPP 定位模型及INS 误差方程，构建了BDS-3 PPP/INS 紧组合滤波模型，使用车载实测数据进行了BDS-3 PPP、BDS-3 PPP/INS 松组合、BDS-3 PPP/INS 紧组合三种模式的定位精度评估.

1 BDS-3 PPP/INS 紧组合模型

1.1 BDS-3 PPP 定位模型

无电离层载波相位及伪距观测方程为

式中：IF表示无电离层组合，其不仅可以消除一阶电离层延迟，而且解算原理简单；λIF为无电离层组合的波长；为无电离层组合的整周模糊度；表示接收机与卫星之间的距离；tr为接收机钟差；ts为卫星钟差；Ts为对流层延迟；为无电离层组合的载波相位观测噪声和伪距观测噪声；分别为接收机端及卫星端的伪距硬件延迟，精密钟差及精密星历产品均采用伪距计算，产品中已经包含了伪距硬件延迟，所以在实际处理中被接收机和卫星钟差吸收；分别为接收机端及卫星端的载波相位硬件延迟，被整周模糊度吸收.对流层延迟可以分为对流层干延迟Th和湿延迟Tw，mh、mw表示对应对流层延迟的投影函数，可简化为

式中：e为从接收机位置指向卫星位置的方位余弦矢量，re表示地心地固坐标系下坐标向量；c为光速.

1.2 INS 误差方程

惯性导航机械编排方程是惯性导航的基础，由位置、速度、姿态微分方程组成，本文INS 在地心地固坐标系下进行解算.惯性导航微分方程可以表示为

1.3 BDS-3 PPP/INS 紧组合滤波模型构建

在BDS-3 PPP 定位模型及INS 误差的基础采用扩展卡尔曼滤波(EFK)解算方法构建紧组合滤波模型，紧组合滤波解算方法可以满足卫星数量不足条件下位置、速度解算，同时可以准确给出观测噪声方差，获得更高定位精度.但是紧组合滤波解算方法由于状态参数中涉及整周模糊度，增大了计算量，所以采用后处理方式解算.

1.3.1 BDS-3 PPP/INS 状态方程

联合INS 系统模型及PPP 状态方程得到PPP/INS 紧组合滤波模型的状态参数δx(t)及噪声向量w(t)：

1.3.2 BDS-3 PPP/INS 观测方程

由BDS-3 PPP 定位模型可以得到PPP/INS 紧组合滤波模型的观测方程.

式中：δZ(t)为系统的观测向量，由卫星载波相位或伪距观测值减先验距离组成；H(t)、v(t)为观测矩阵和噪声矩阵.

式中：E为 接收机到BDS 卫星方向余弦的列矩阵；M为湿延迟投影函数.

2 实地实验分析

2.1 实验背景

使用2022 年7 月2 日河南省郑州市的跑车实验数据，实验采用组合导航系统(XWYD-7960)的内置惯性设备及司南导航M300 Pro 接收机，实验中所用车载实验平台及实验设备如图1 所示.接收机采样频率为1 Hz，惯导采样频率为100 Hz.实验的轨迹如图2 所示，整个实验过程中均为宽阔马路，两侧无严重遮挡，保证了实验数据的质量.惯导设备性能参数：陀螺仪零偏为1(°/h)，角速度随机游走为0.05(°/h)，加速度计零偏为0.5×10-3g，速度随机游走为2×实验数据总时长为3 600 s，参考值使用Inertial Explorer 8.60 软件RTK/INS 紧组合平滑解.BDS卫星数量如图3 所示.

图1 车载实验平台及惯导、接收机设备图

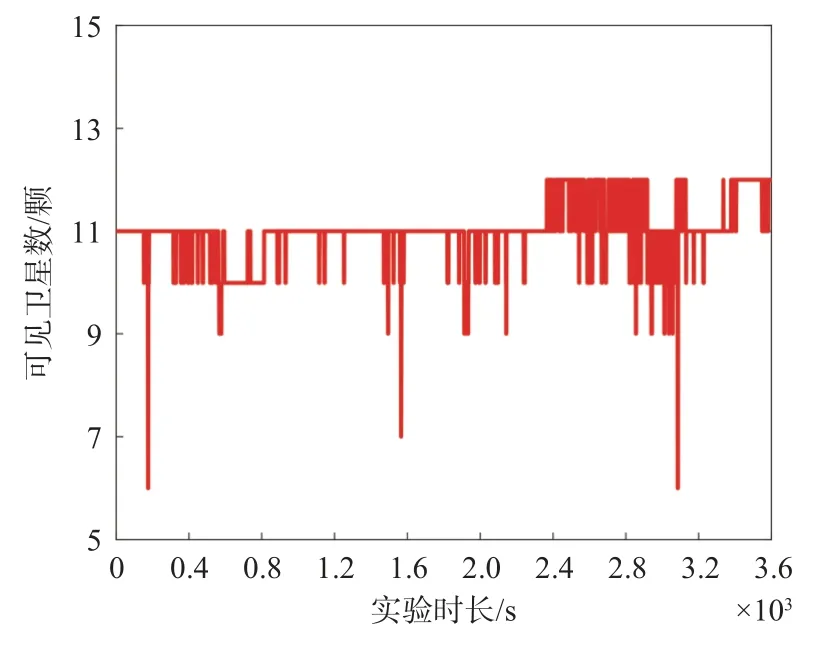
图3 可观测BDS 卫星数量图

2.2 实验性能分析

跑车实验数据中仅使用BDS 卫星，实验中首先进行3 min 静态初始对准，而后进行动态实验.本实验采用三种数据处理方案进行数据处理：1)BDS-3 PPP 解算；2)BDS-3 PPP/INS 松组合解算；3)BDS-3 PPP/INS 紧组合解算，并将三种处理方案结果与参考值做差即可得到东(E)、北(N)、天顶(U)方向的位置、速度、姿态误差结果如图4～5 所示.可以发现，位置、速度、姿态误差均在最后20 min 保持稳定，所以本文中所给精度统计值为最后20 min 所对应的均方根误差(RMSE).

图4 BDS-3 PPP、BDS-3 PPP/INS 松组合和BDS-3 PPP/INS 紧组合位置误差时间序列图

图4 给出了BDS-3 PPP、BDS-3 PPP/INS 松组合及BDS-3 PPP/INS 紧组合的E、N、U 方向位置误差，从图中可以明显看出BDS-3 PPP/INS 紧组合的位置精度最高.表1 中给出三种处理方案中后20 min E、N、U 方向位置误差的RMSE，可以得出BDS-3PPP/INS松组合位置精度与BDS-3 PPP 基本一致，三个方向位置精度均在15 cm 以内.BDS-3 PPP/INS 紧组合在E、N、U 方向位置精度均保证在厘米级，其中E 方向位置精度最高，并且较BDS-3 PPP/INS 松组合位置精度分别提升38.3%、33.1%、35.6%.

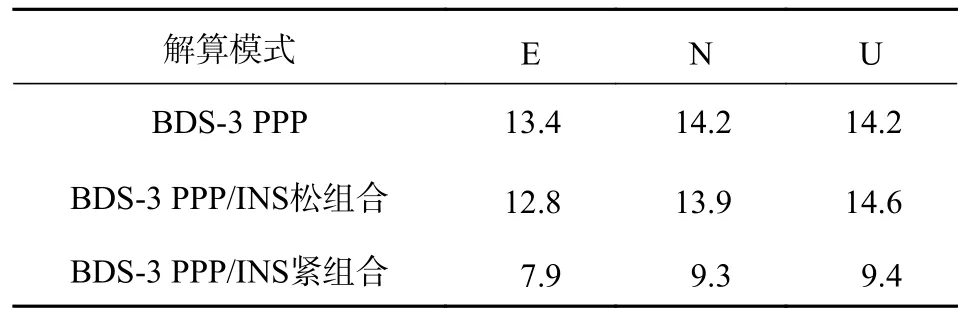
表1 三种处理方案位置的RMSE 统计 cm

可以看出，两种组合中U 方向速度误差波动最小，BDS-3 PPP/INS 松组合在三个方向均存在波峰，误差最高达到4.43 cm/s，而BDS-3 PPP/INS 紧组合三个方向波动明显小于BDS-3 PPP/INS 松组合表2中BDS-3 PPP/INS 紧组合对于U 方向速度精度提升最小，对N 方向速度精度提升最明显，较BDS-3 PPP/INS 松组合三个方向分别提升27.3%、45.8%、12%.

表2 两种处理方案速度、姿态的RMSE

图5(b)中给出两种BDS-3 PPP/INS 组合方式的横滚角、俯仰角、航向角的姿态误差随时间的变化，可以看出，BDS-3 PPP/INS 两种组合方式姿态误差随时间变化曲线基本一致，说明BDS-3 PPP/INS 紧组合并未对BDS-3 PPP/INS 松组合姿态误差进行明显改进.从表2 中的姿态精度同样可以发现，BDS-3 PPP/INS 紧组合与BDS-3 PPP/INS 松组合横滚角、俯仰角、航向角精度相当.

图5 BDS-3 PPP/INS 松组合和紧组合两种误差时间序列图

3 结束语

本文首先针对BDS-3 PPP/INS 紧组合模型展开了研究，详细推导了BDS-3 PPP 定位模型及地心地固坐标系下的INS 误差方程，并采用EFK 算法构建BDS-3 PPP/INS 紧组合滤波模型.本文利用最新2022 年7 月实测车载数据对BDS-3 PPP/INS 紧组合定位性能进行分析，将实验数据分别采用BDS-3 PPP、BDS-3 PPP/INS 松组合及BDS-3 PPP/INS 紧组合三种方案进行处理，可以得到：在位置误差方面，BDS-3 PPP/INS 松组合位置误差精度与BDS-3 PPP相当，BDS-3 PPP/INS 紧组合位置精度为分米级，相较于BDS-3 PPP/INS 松组合分别提升38.3%、33.1%、35.6%.在速度误差方面，较BDS-3 PPP/INS 松组合，BDS-3 PPP/INS 紧组合在E、N、U 方向速度精度分别改进27.3%、45.8%、12%.在姿态误差方面，BDS-3 PPP/INS 紧组合与BDS-3 PPP/INS 松组合姿态误差精度相当.