寒冷地区汽车关键部位运行寿命可靠性数学建模研究
张永华
(安康职业技术学院 基础教学部,安康 725000)
引言
汽车在行进过程中,当处于不同温度地区时,其自身部件的故障率与可靠性均会发生变化[1]。在低温条件下,当汽车行驶速度加快,其车轮材料的断裂韧性开始下降。而在低温、严寒地区,降雨、降雪等气候条件下,车轮很容易发生打滑[2],引发车轮疲劳破坏,从而降低了关键部件的使用寿命和可靠性。
通过判定汽车关键部件的失效情况,可以得出该部件的故障损坏或报废时间[3,4]。因此,可依据部件失效情况,获取其运行寿命与可靠性。有较多学者对部件的运行寿命与可靠性进行了分析,例如舒爱梅等[5]分析了温度场分布下汽车排气系统振动疲劳寿命,利用双向流固耦合等数值计算了温度场的分布,采用Dirlik 估计法估算了汽车排气系统的振动疲劳寿命。Reza 等[6],研究了轴向和多轴变幅载荷条件对汽车转向节疲劳寿命评估的影响。该方法考虑了不同的载荷工况,使用效应力准则的概率方法通过瞬态动力学分析提取的转向连杆根部应力张量的时程评估部件的疲劳寿命。
为了进一步明确寒冷低温对汽车部件疲劳寿命的影响,本文研究了寒冷地区汽车关键部位运行寿命可靠性数学建模,利用数学模型实现多种温度下的汽车关键部位运行寿命可靠性。
1 汽车关键部位运行寿命可靠性数学建模
1.1 摩擦温升数学模型
寒冷地区汽车关键部位在运行时会同接触范围产生摩擦升温,摩擦热通过接触表面向关键部件内部传输,同时同周围环境完成辐射换热,利用公式(1)描述摩擦热的导热过程:
式中:
T—汽车关键部位温度;
ρ—汽车关键部位材料密度;
c—汽车关键部位材料质量热熔;
λ—热导率;
∇—Hamilton 算子。
因为受到寒冷天气下低温环境的影响,使得汽车关键部件的接触范围出现一定的温差,汽车运行过程中,关键部件同接触部件间存在热量变换关系,通过全局换热系数描述该种热量变换关系,则有:
式中:
enw、 enr—汽车零部件同接触面的法向矢量;
Tw、Tr—汽车零部件和接触面的表面温度;
h—汽车零部件非接触区域同周围环境的传热吸收。
用式(4)描述汽车零部件的非接触区域表面同周围环境的导热情况:
式中:
T0—环境温度。
1.2 温度范围的确定
外界环境条件不同,以及汽车零部件自身存在一定的发热温度,使得汽车零部件承受的温度区间存在较高的差异。依据标准QC/T 413-1999《汽车电气设备基本技术条件》规定的汽车电气产品温度范围,设置低温条件下汽车零部件可靠性寿命的温度范围。因为本文研究寒冷地区汽车关键部位运行寿命可靠性,研究的温度是不断波动的,因此依据国家标准GB 2423.22-87《电气电子产品基本环境实验规程实验N:温度变化实验方法》中的实验Nb:设定的温度波动速率情况,本文设置寒冷地区汽车零部件的温度变化范围见表1。

表1 汽车零部件的温度范围
1.3 汽车关键部位失效数据经验取值
在建立汽车关键部位运行寿命可靠性数学模型过程中,需要利用其失效数据的经验分布函数近似值替代总体分布。此时需要依据汽车关键部位的失效数据,先计算得到经验函数值,按照时间顺序,可将其失效时间排列为: t1< t2< ... < ti,其中, i =1,2,3,...,m 表示从小到大排序得到的汽车关键部位的寿命序号,即为失效秩次。若汽车关键部位失效数据数量较大,达到n ≥20时,则可通过公式(1)计算其经验分布函数:
若汽车关键部位失效数据数量较低时,通过公式(5)计算会引起误差较大,因此,可继续通过公式(6)计算:
公式(6)属于一种近似中位秩公式。若统计的汽车关键部位仍未完全失效,则会出现数据记录不完全现象[7-9]。此时,每个关键部位的i 值并没有确定值,因此可采用平均秩次法,对汽车关键部位的经验分布函数进行计算,采用公式(7)计算平均秩次:
式中:
k—汽车关键部位失效的序列;
Pk—秩次。
当完成平均秩次计算后,将结果引入到公式(6)中,即能够获取汽车关键部位的经验函数值,如公式(8)所示:
1.4 基于威布尔分布的运行寿命可靠性模型
1939 年,瑞典学者Waloddi Weibull 率先提出了威布尔分布模型,在该模型中,具体存在三个参数,依次为形状、尺寸以及位置参数。该模型属于可靠性较高的一种分布模型,本文利用该模型分析汽车关键部位的生存寿命与可靠性。在汽车关键部位中,任一局部失效导致整体失效情况均可以认定为威布尔分布,例如车轴、车轮、空气管路等[10,11]。通过公式(9)描述其概率密度函数:
式中:
β > 0—形状参数,该参数与汽车关键部位失效率变化存在关联;
μ > 0—尺寸参数,该参数与关键部位所承受负载的大小存在关联[12-14],当负载越大,则尺寸参数则会随之降低;
γ —位置参数,即表示当前时刻之前,关键部位的可靠度与1 相等,若γ = 0时,说明三参数模型会转变为两参数模型。通过公式(10)计算该设计下的模型累积失效分布函数:
通过公式(10)可以计算得出汽车关键部位在运行寿命内任意时间下的累积失效率 K ( t ),并通过公式(11)可以计算可靠度函数:
采用公式(11)可以计算得出汽车关键部位在运行寿命内任意时间下的可靠度 K ( t ),同时,可以通过公式(12)计算其失效函数:
通过公式(12)即可计算失效率 h ( t ),同时,利用公式(13)可以计算得出汽车关键部位可靠性寿命:
当设定相应的可靠度时,通过公式(13)即可获取汽车关键部位的寿命值t ( K )。
1.5 汽车关键部位运行寿命可靠性参数估计
本文采用曲线拟合法对汽车关键部位运行寿命可靠性数学模型参数进行估计。在威布尔分布模型中,位置参数γ 与尺寸参数μ 的加和称为示性寿命或示性强度,当失效概率为63.2 %时,两者之和即可以表示汽车关键寿命值或强度值。在进行估计时,该值分散性较小,这是由于当t = γ +μ 时, ( ) 1/K t= e= 36.8 %,当m>1 时,其概率密度函数均为单峰形式[15],而γ +μ 则位于其峰点周围,在此位置下,数据点相对密集,因此可以获取较为精准的γ +μ 估计值。可将公式(9)表示为以下形式:
公式(14)中,c 表示示性寿命;设X = t - c,Y =K ( t),由此可将公式(14)调整为:
在公式(15)中,并不存在极大似然估计值,因此,在此时利用origin 拟合,通过其非线性拟合能力,对函数进行编辑,设定函数初始值,之后进行不断迭代,由此获取μ 与β 的估计值,而γ 的估计值则为c -μ 。也可以直接通过origin 非线性拟合,直接拟合公式(9),当设定初始参数后开始迭代,可直接获取三个参数。
2 仿真分析
利用本文模型模拟汽车关键部位的运行寿命与可靠性,采取可靠性试验,并对实验结果做出统计处理,以获取可靠性指标,同时进行多温度条件下的模拟实验,获取寒冷地区的汽车关键部位运行状态。
2.1 参数变化影响分析
分析三个模型参数对概率密度函数的影响。针对形状参数进行详细分析,分析当位置参数与尺寸参数不变时,形状参数的改变会对汽车关键部位失效情况的影响,分析结果如图1 所示。
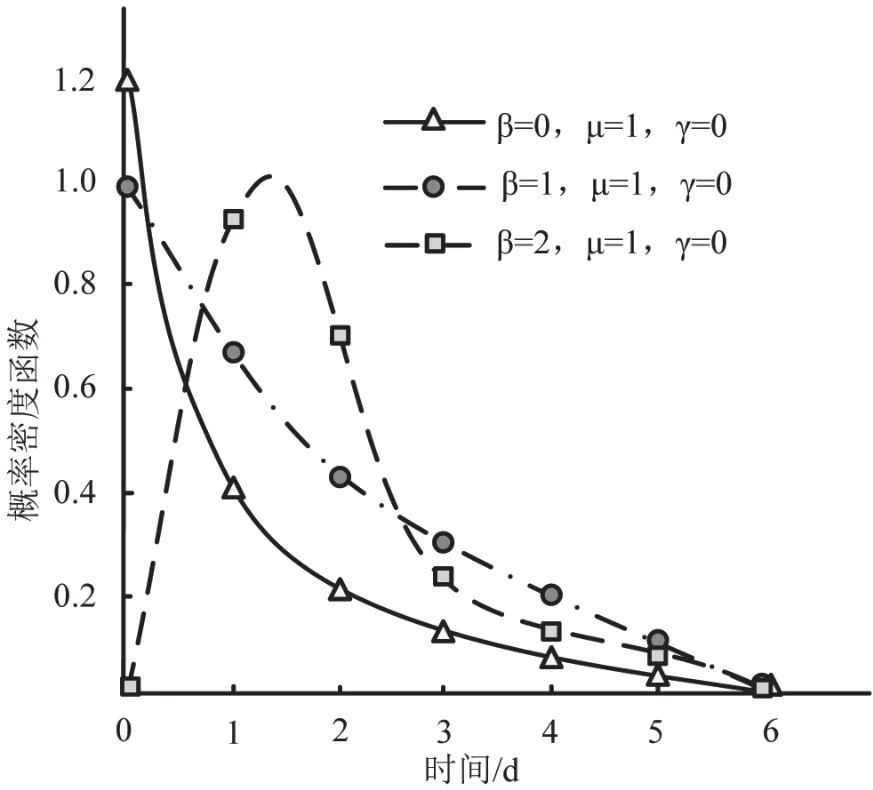
图1 形状参数改变时对概率密度函数的影响
由图1 可以看出,当形状参数小于1 时,随着时间的增加,概率密度值会迅速降低,当下降到一定幅度后,开始缓慢降低,说明失效率会随之递减,表示汽车关键部位存在早期失效特征;当形状参数等于1 时,威布尔分布呈现指数分布,存在恒定失效率,即汽车关键部位会出现偶然失效期;当形状参数大于1 时,随着时间增加,概率密度函数呈现先增大后减小,说明在该参数下,汽车关键部位处于老化期。
分析尺寸参数变化对汽车关键部位失效分布的影响,当该参数发生改变时,其他参数不变,分析概率密度参数的变化情况,分析结果如图2 所示。

图2 尺寸参数变化对汽车关键部位失效的影响
根据图2 可知,当尺寸参数处于0 时,汽车关键部位的寿命十分短暂,表示关键部位所受负载较大;而当尺寸参数为1 时,汽车关键部位的寿命相对延长,但在尺寸参数为2 时,寿命明显增大,说明当尺寸参数越大,汽车关键部位的寿命越长。
分析位置参数变化对汽车关键部位失效分布的影响,当该参数发生改变时,设定尺寸参数为1,形状参数为2,分析概率密度参数的变化情况,分析结果如图3 所示。
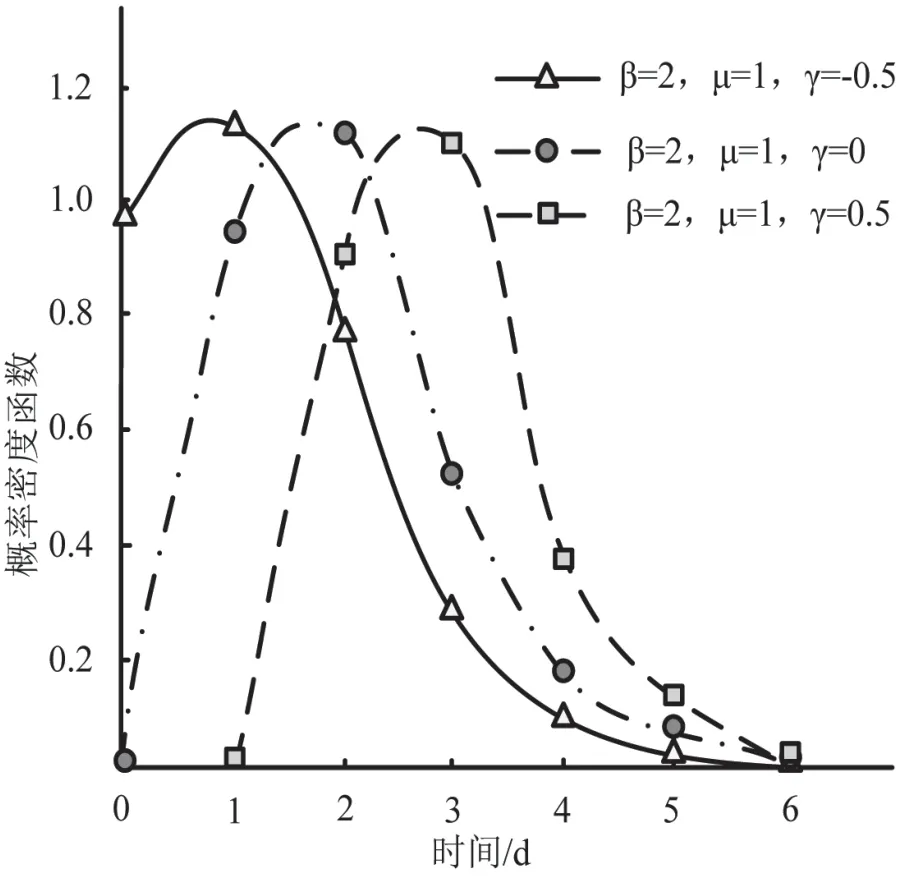
图3 位置参数变化对汽车关键部位失效的影响
根据图3 可知,位置参数对概率密度的影响在时间轴中平移,当位置参数由-0.5 经0 变化至0.5 时,汽车关键部位故障出现时间逐渐延长。
2.2 汽车关键部位运行寿命可靠性分析
分析利用本文模型对汽车关键部位运行寿命进行建模,通过威布尔概率纸描点展示建模后的关键部位失效情况,由此分析汽车关键部位的运行寿命,分析结果如图4 所示。
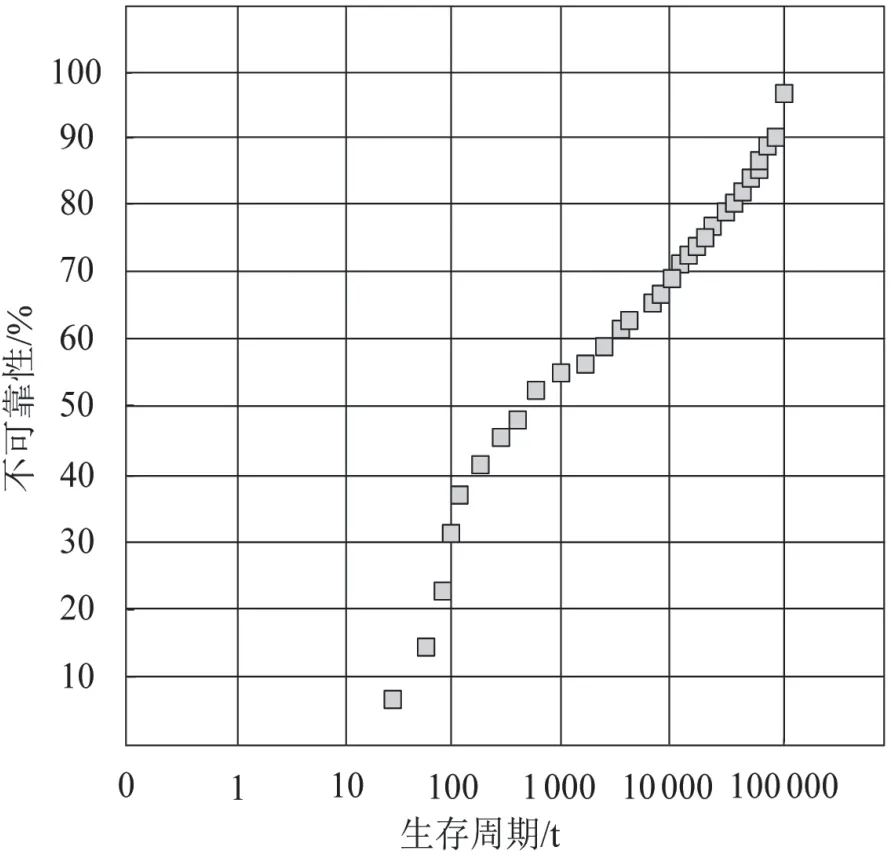
图4 应用本文模型建模结果
根据图4 可知,该汽车关键部位的失效情况在生存周期期内随着时间增加逐渐上升,最终达到失效,说明当运行时间越久,该关键部位的可靠性越低,应用本文方法,可对汽车运行失效情况清晰建模,获取精准的汽车关键部位运行寿命。
2.3 运行寿命可靠性分析
依据以上构建的寿命模型,对汽车关键部位进行可靠性估计,通过公式(7)可以计算得到关键部位在寿命期内任意寿命点的可靠度,依据该公式,分析当汽车里程逐渐增加时,汽车关键部位的可靠性变化情况,分析结果如图5 所示。
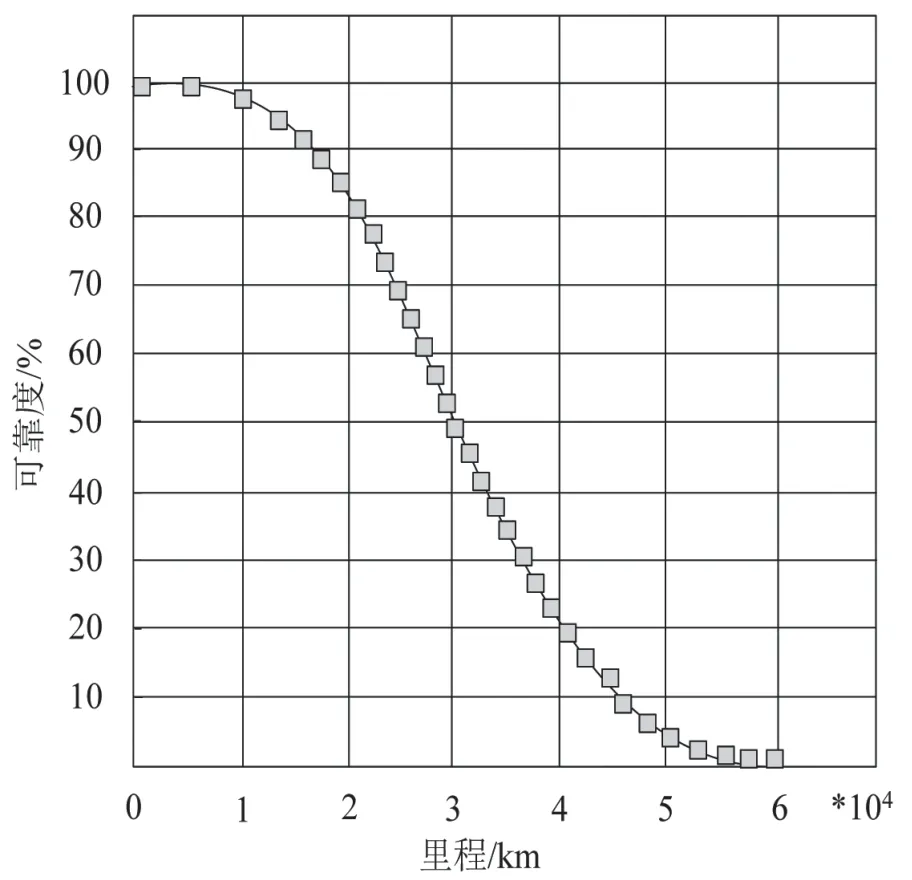
图5 可靠度分析
根据图5 可知,当行驶里程不断下降,本文模型分析得到的汽车关键部位可靠度也会随之下降,这说明汽车关键部位的寿命值在到达一定里程后会逐渐结束,导致该部位需要更换,即关键部位的失效率逐渐递增,说明汽车关键部位存在老化特征,通过本文模型,可精确分析汽车关键部位的可靠度。
2.4 低温寒冷地区汽车关键部位运行情况分析
以汽车车轮为关键部件,统计其在低温寒冷条件下的静拉伸能力、疲劳性以及裂纹情况。
1)低温寒冷地区汽车车轮材料静拉伸能力分析
利用本文模型,按照国家标准GB/T 13239-2006 进行低温寒冷地区车轮材料静拉伸模拟,测定材料的低温拉伸性能,设定低温条件为-45 ℃,模拟材料压力并缓慢加压,直至车轮的轮辐与轮辋材料发生断裂,并利用本文模型绘制-45 ℃条件下,汽车车轮轮辐与轮辋材料的拉伸变化图,如图6 所示。
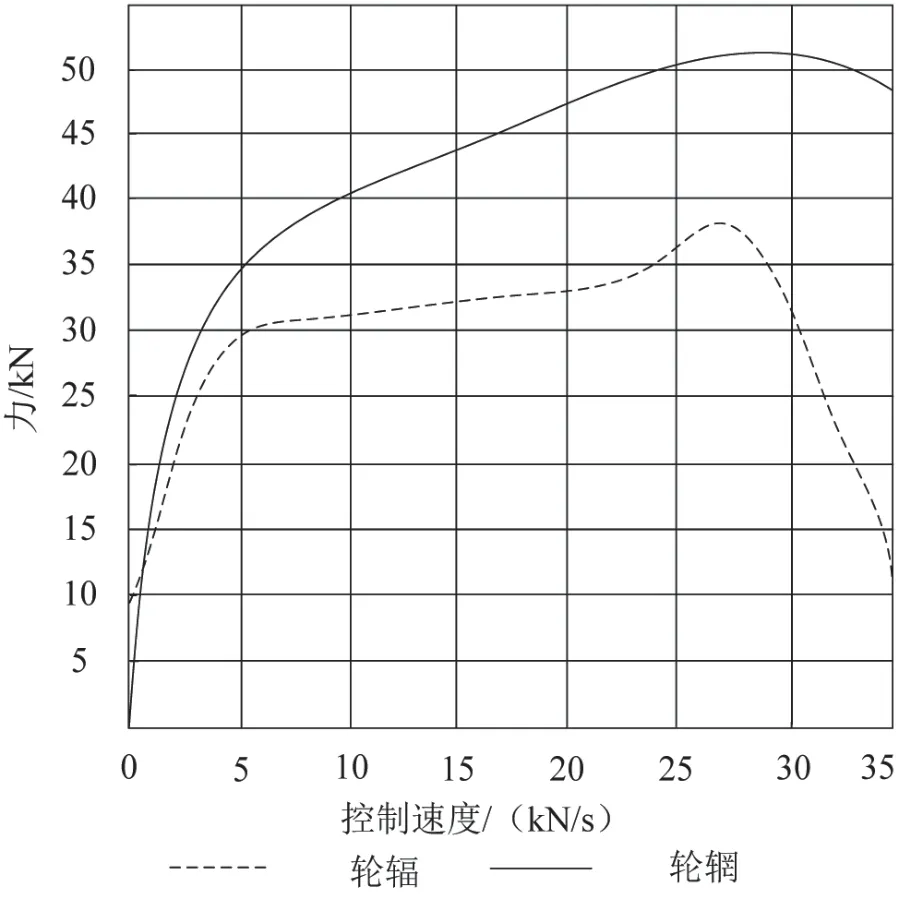
图6 -45 ℃条件下汽车车轮轮辐与轮辋材料静拉伸曲线
由于静拉伸实验过程中,实验的结果会存在一定幅度的波动,因此,本文按照图6 的拉伸变化,选取3 个汽车车轮材料进行分析,并按照不同部位的均值作为实验结果,分析结果如表1 所示。
根据表1 可知,轮辐的屈服、抗拉强度依次为498 MPa 与917 MPa,而轮辋的性能则与轮辐存在一定的区别,轮辋的屈服强度为584 MPa,明显高于轮辐,而其抗拉强度为989 MPa,同时相较于轮辐也略高出一些,由此可以看出,轮辋部位的性能要明显高于轮辐,在低温寒冷地区轮辋的运行寿命与可靠性相对要高。

表1 -40 ℃条件下轮辐与轮辋部位的静拉伸性能
2)低温寒冷地区汽车车轮疲劳性分析
通过本文模型模拟低温寒冷地区汽车车轮部位的疲劳性,按照疲劳试验设计规范,设置模拟实验参数,如表2 所示,按照表2 的实验标准,分析车轮部位的疲劳极限。

表2 -45 ℃低温寒冷情况下车轮部位实验参数
模拟8 个轮辐与8 个轮辋进行实验,分析这两个部位出现断裂或越出时的应力,以获取轮辐与轮辋的疲劳极限,分析结果如图7 所示。
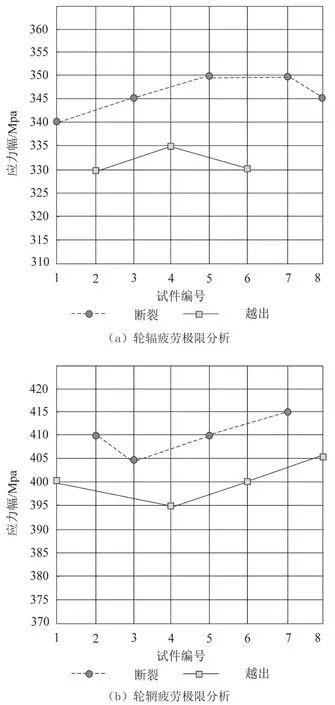
图7 轮辐与轮辋的疲劳极限分析
根据图7 可知,轮辋与轮辐在应力值较高的情况下会出现断裂现象,其中,轮辋的疲劳极限要明显大于轮辐,轮辐在试验过程中,试件5 与试件7 的疲劳极限最大,达到350 MPa,而轮辋在试验时的疲劳极限最高为415 MPa,由此可以看出,在寒冷地区条件下,轮辋的疲劳极限较大,因此其运行寿命要高于轮辐。
3)低温寒冷地区条件下车轮部位裂纹情况分析
利用本文模型模拟10 个轮辋试件在不同温度下的起裂门槛值,以此获取轮辋的开裂情况,分析结果如表3所示。
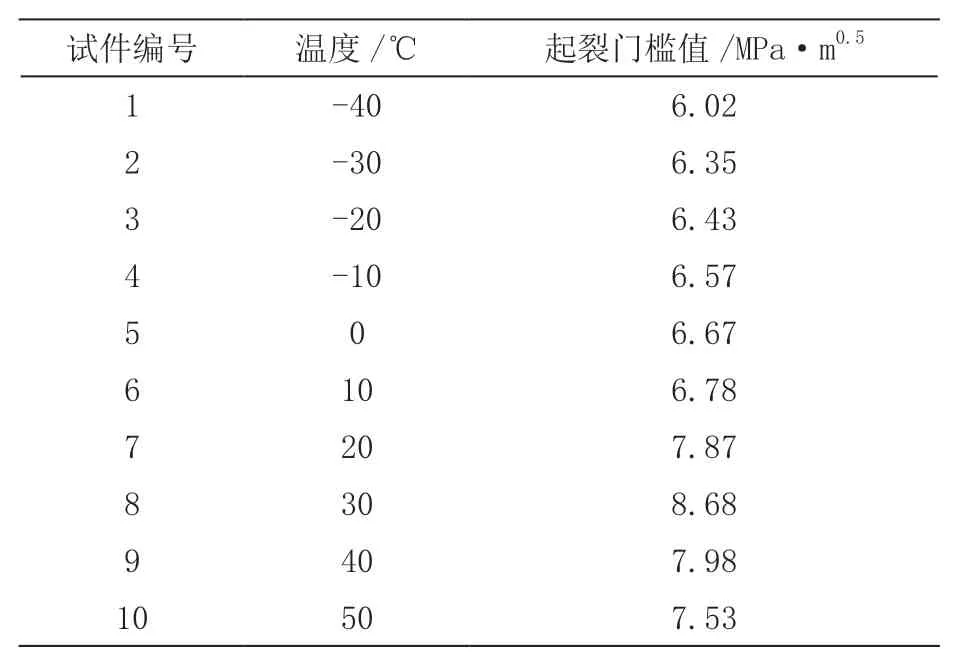
表3 不同温度下轮辋裂纹情况分析
根据表3 可知,当试件处于30 ℃时,该汽车部位的起裂门槛值最高,说明30 ℃条件下,该部位的寿命与可靠性最大,当气温大于30 ℃时,起裂门槛逐渐开始下降,而气温低于30 ℃时,起裂门槛同样呈下降趋势,在气温为-40 ℃时,起裂门槛达到6.02 MPa·m0.5,说明当应力处于6.02 MPa·m0.5时,该轮辋开始出现断裂。
3 结论
本文研究寒冷地区汽车关键部位运行寿命可靠性数学建模,通过构建汽车关键部位运行寿命可靠性的数学模型,模拟分析低温寒冷条件下汽车关键部位的变化情况,以此获取汽车各部位的运行寿命与可靠性,并通过大量模拟实验,获取精准的汽车部位运行寿命。在未来研究中,可利用当前研究结果,继续进行实验分析,使该数学模型的验证结果更加充分。

