气温变化“奇遇记”

文／于杰

同学们有根据天气预报提前准备好更换衣物的经历吗？事实上，气温不仅影响着我们的生活，而且在指导农业种植、工业生产等方面都具有重要意义。下面，我们就跟随教材中一道有关气温的习题，通过变式感受气温变化中的统计知识吧！

原题 （苏科版数学教材九年级上册第116 页练习3）某市2011 年、2012 年3 月上旬的日最高气温（℃）如下：

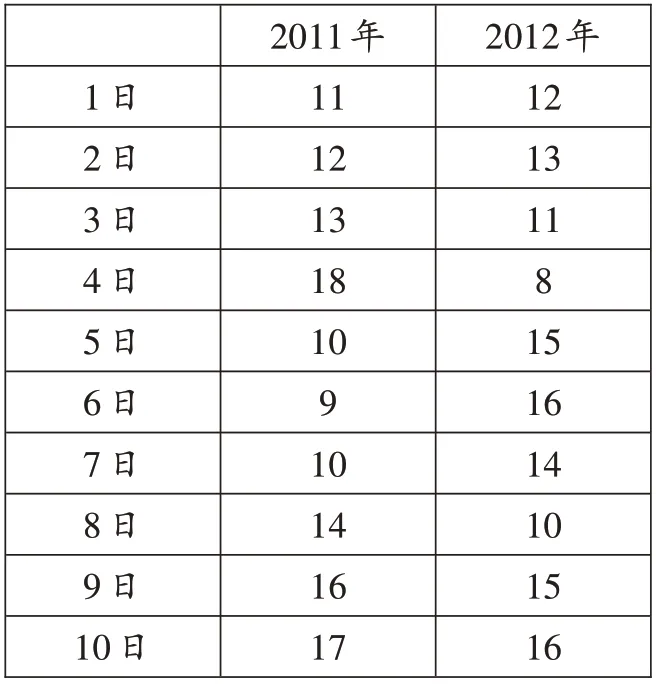
______________________________1日______________________________2日______________________________3日4日5日_______________________________6日_______________________________7日______________________________8日______________________________9日_____________________________10日___________________________________2012年12 13 11 8 15 16 14 10 15 16 2011年______________11________________12________________13________________18 10 9_________________10_________________14________________16________________17________________

该市这两年中，哪一年3 月上旬的最高气温比较稳定？为什么？

【分析】生活中，我们除了关注数据的集中趋势外，还关注数据的离散程度，而方差就是用来刻画数据稳定性的统计量。由于本题需要我们比较哪一年3 月上旬的最高气温比较稳定，因此通过计算方差能够精确地反映。

解：该市2011 年3 月上旬日最高气温的方差为9（℃2），2012 年3 月上旬日最高气温的方差为6.6（℃2）。因此，该市2012 年3 月上旬的日最高气温比较稳定。

变式1 某地连续五天每天最高气温与最低气温记录如下表所示：

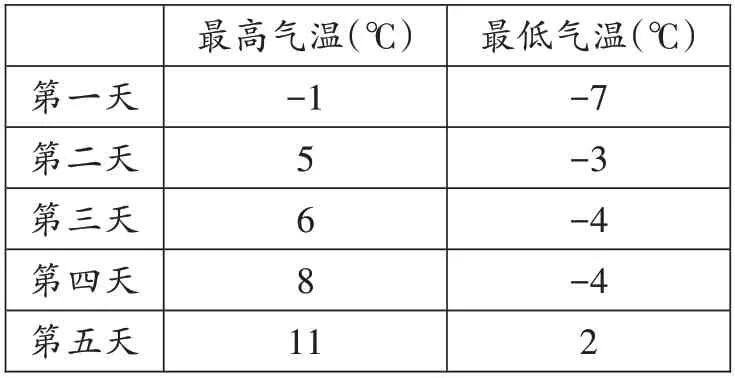
_____________________________最低气温（℃）______________________________-7______________________________-3______________________________-4_______________________________-4________________________________2第一天________第二天________第三天________第四天_________第五天________最高气温（℃）________________-1______________________5______________________6______________________8_______________________11_______________________

第几天的温差（最高气温与最低气温的差）最大？第几天的温差最小？关注温差对我们的生活有何帮助？

【分析】温差是最高气温与最低气温的差，也就是极差。关注温差不仅能知晓一天中温度变化的稳定性，而且会影响人们依赖气温的日常行为活动。

解：第一天，-1-（-7）=6（℃）；第二天，5-（-3）=8（℃）；第三天，6-（-4）=10（℃）；第四天，8-（-4）=12（℃）；第五天，11-2=9（℃）。其中第四天的温差最大，第一天的温差最小。关注温差对于我们添衣、减衣具有指导意义。

变式2 随机抽取某市一年（按365 天计）中的30天平均气温状况，如下表：

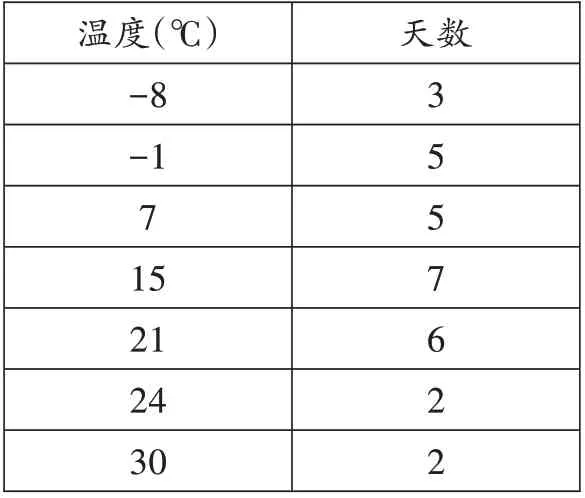
____温_______________度（℃）____________________________-8____________________________-1_____________________________7____________________________15____________________________21____________________________24____________________________30天数______3_______5_______5_______7_______6_______2_______2_______

请根据上述数据回答问题：

（1）该组数据的中位数是什么？

（2）若气温在21℃～24℃为市民“满意温度”，则该市一年中达到市民“满意温度”的天数大约有多少天？

【分析】此题考查了求中位数和用样本估计总体的方法。其中，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），用样本估计总体需要先根据频数除以数据总数计算频率，再用总体数量乘该频率即可。

解：（1）该组数据的中位数是第15、16 个数的平均数，即（15+15）÷2=15（℃）；（2）该市一年中达到市民“满意温度”的天数约有365×≈97（天）。

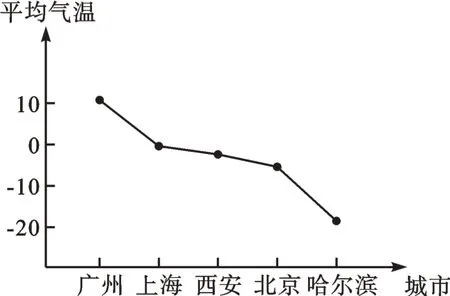
真实情境变式 根据中国气象局发布，我国几个城市某天的平均气温如下表所示。你能发现什么规律？

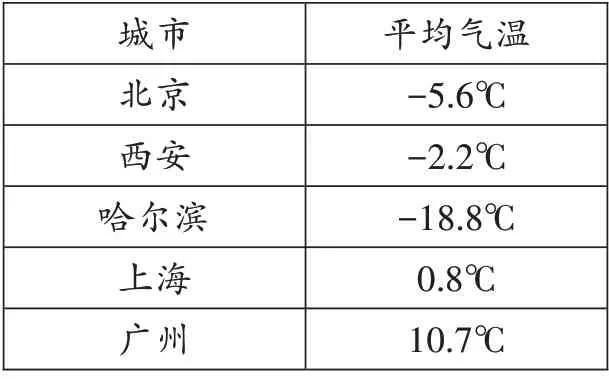
_______________________平均气温_______________________-5.6℃_______________________-2.2℃_____________________-18.8℃________________________0.8℃_________________________10.7℃城市______________________北京______________________西安______________________哈尔滨_____________________上海______________________广州_______________________

当面对一组真实情境下的数据时，你会如何处理？如果仅观察这张表格，你会发现不同城市的气温之间并不存在明显规律，这是因为现实生活中影响一个事物的因素有很多，它们渗透着不同学科的各个方面。通过地理学科的学习我们知道，不同城市在地球上分布位置不同，而气温也与所在区域位置有关。那么请问同学们，你会用什么工具来研究城市与气温的关系呢？没错，我们可以在地图上找到这几个城市的位置，将它们从南到北进行排列，并依次记录为广州、上海、西安、北京、哈尔滨。

接下来，我们按照以上顺序，利用城市与平均气温设计一个统计图，同学们认为选择哪一种统计图比较合适呢？相比于条形统计图与扇形统计图，折线统计图更能看出气温的变化趋势。在画出统计图后，我们发现城市气温与地理位置存在密切联系，由南向北气温是逐渐降低的。看来统计知识不仅能帮助我们解决数学问题，还能解释生活中的现象，是一个很棒的数学工具！