探究问题本质 发展核心素养

庄芹

三角函数的概念是高中数学的难点之一，是高中继指数函数、对数函数和幂函数之后学习的函数，是函数的一个下位概念。它是一种重要的基本初等函数，既是解决实际问题的重要工具，也是学习数学中其他知识的基础。本文是笔者将讲授三角函数概念的整体思路与过程整理而成的内容。

一、教学内容

（一）内容分析

本节课是《三角函数》一章的概念课，具有核心地位，起着统领全局的作用。在此之前，学生已经学习了锐角三角函数、任意角和弧度制，初中也对三角函数（正弦、余弦、正切）有了一定的了解。这些都为本节课的学习提供了知识准备。本节将学习任意角三角函数的概念和表示。借用单位圆直观地表示三角函数的对应值。本节课与学生以往的经验有很大不同，认识上必须破除思维定式，帮助学生弄清三角函数的“三要素”，特别是要先明确“给定一个角，如何得到对应的函数值”的操作过程，然后再给定义。这是在一般函数概念引导下的“下位学习”，不仅使三角函数概念的引入水到渠成，而且由三角函数对应关系的独特性，可以使学生再一次认识函数的本质。

（二）课标要求

借助单位圆理解任意角的正弦、余弦、正切的定义。

（三）学习目标

1.知道三角函数是刻画现实世界中有“周而复始”变化规律现象的数学工具。能通过借用单位圆上的点的运动，建立一个数学模型，刻画点P的位置变化情况。能知道在直角坐标系下，建立函数模型。

2.能分析出单位圆上点的旋转中涉及的量及其相互关系，体会函数概念引导下的“下位学习”。

3.通过自主探究，感知任意角三角函数的概念和初中锐角三角函数定义的相通性，体会到学习的知识是螺旋上升的。

4.能根据三角函数的概念求出给定角的三角函数值。掌握求任意角三角函数一般方法。

5.通过探究了解任意角三角函数的另外一种定义，能在已知角终边上任意一点坐标的情况下，求出角的各三角函数。

6.通过探究三角函数概念独特的生成过程，体会数学建模和数学运算的基本核心素养。

（四）教学重点

本节的重点是利用单位圆模型理解任意角三角函数概念的形成过程。

二、教学过程

（一）课前准备

引导学生回顾函数的定义，函数的表示法：

一般地，设A，B是非空的实数集，如果对于集合A中的任意一个数x，按照某种确定的对应关系f，在集合B中都有唯一确定的数y和它对应，那么就称f：A→B为从集合A到集合B的一个函数，记作y=（f x），x∈A。

其中，x叫作自变量，x的取值范围A叫作函数的定义域。与x的值相对应的y值叫作函数值，集合{ f（x）|x∈A}叫作函数的值域。

（二）课中学习

1.创设情境，明确背景

引导语：现实世界中的许多运动、变化都有着循环往复、周而复始的规律，这种变化规律被称为周期性。例如：地球自转引起的昼夜交替变化和公转引起的四季交替变化、月亮圆缺、潮汐变化，物体做着匀速圆周运动时的位置变化，物体做着简谐振动时的唯一变化，交变电流变化等。

提出问题：匀速圆周运动是现实生活中周期现象的代表，在前面的学习中，我们知道函数是描述客观世界变化规律的重要数学模型，那么匀速圆周运动的规律该用什么函数模型刻画呢？

学习任务：单位圆上的点P以A 为起点，做逆时针方向旋转，建立一个函数模型，刻画点P的位置变化情况。

思考1：单位圆上点P以A 为起点，做逆时针方向的旋转，在把角的范围推广到任意角，并在弧度制下把角推广到全体实数后，怎样刻画点P的位置变化？（检测学习目标1）

如图1，以單位圆的圆心O为原点，以射线O住为x轴的非负半轴，建立直角坐标系，点A的坐标为蓸1，0 蔀，点P的坐标为蓸x，y蔀，射线O住从x轴的非负半轴开始，绕点O按逆时针方向旋转角琢，终止位置为OP。

2.分析具体事例，归纳共同特征

思考2：当角琢确定，它的终边与单位圆的交点P确定吗？点P的坐标确定吗？（检测学习目标2）

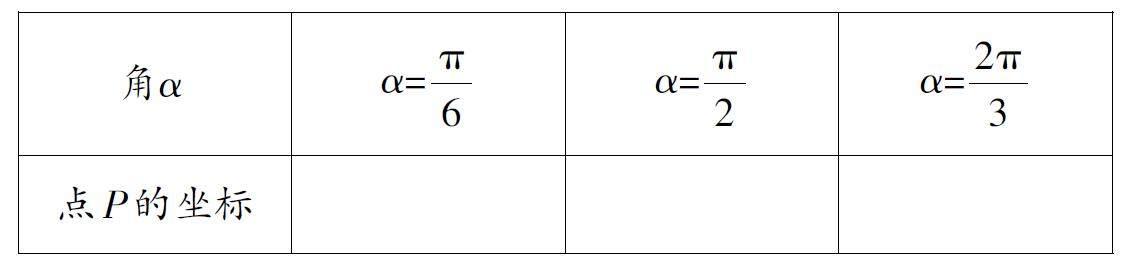
问题1：当α=π/6 时，点P的坐标是什么？（检测学习目标2）

问题2：当α=π/2 或2π/3 时，点P的坐标又是什么？

思考3：你所求出的这三个角的坐标，它们是唯一确定的吗？（检测学习目标2）

引导学生把这个问题推广到更一般的情形，角的范围是任意角。

向学生提出问题：一般地，任意给定一个角琢，它的终边庄P与单位圆交点P的坐标能唯一确定吗？（教师通过几何画板进行动态展示）（检测学习目标2）

追问：你能用函数的语言来刻画这种对应关系吗？

对于R中的任意一个角琢，它唯一对应一个终边位置OP，唯一对应一个与单位圆的交点P蓸x，y 蔀，无论是横坐标x，还是纵坐标y，都是唯一确定。

这有两个对应关系：

f：实数a（弧度）对应于点P的纵坐标y；

g：实数a（弧度）对应于点P的横坐标x。

根据上述分析：

f：R→［-1，1］和g：R→［-1，1］都是从集合R到集合［-1，1］的函数。

设α是一个任意角，α∈R，它的终边OP与单位圆相交于点P（x，y）。

（1）把点P的纵坐标y叫作琢的正弦函数，记作sinα，即y=sinα。

（2）把点P的横坐标x叫作α的余弦函数，记作cosα，即x=cosα。

（3）把点P的纵坐标与横坐标比值y/x叫作P的正切函数，记作tanα，即y/x=tanα（x≠0）。

思考：这里给出的正切，是不是也是函数？（检测学习目标2）

可以看出，当α=π/2+kπ（k∈Z）时，α的终边落在了y轴上，这时点P的横坐标等于0，所以yx=tanα无意义。除此之外，对于确定的角α，y/x的值也是唯一确定的。所以y/x=tanα（x≠0）也是以角为自变量，以单位圆上点的纵坐标与横坐标的比值y/x为函数值的函数，称为正切函数。

故正弦、余弦和正切函数都是以角为自变量，以单位圆上点的坐标或坐标比值为函数值的函数。我们将正弦函数、余弦函数和正切函数统称为三角函数，通常将它们记为：

正弦函数：y=sin x，x∈R

余弦函数：y=cos x，x∈R

正切函数：y=tan x，{x|x≠kπ+π/2 ，k∈Z}

3.任意角三角函数与锐角三角函数的联系

在初中时已经学了锐角三角函数，知道它们都是以锐角为自变量，以比值为函数值的函数。设x∈（0，π/2），把按锐角三角函数定义求得的锐角x的正弦记z1，并把按本节三角函数定义求得的x的正弦记为y1。那么z1与y1相等吗？对于余弦、正切也有相同的结论吗？

课堂上学生只要证明出正弦即可，余弦和正切的推导可让学生课后再进行。

【设计意图】建立锐角三角函数和任意角三角函数的联系，使学生体会两个定义的和谐性。明白我们所学的知识是螺旋上升的。

4.任意角三角函数概念的初步应用

例1：如图2，求5π/3正弦、余弦和正切值。（检测学习目标4）解：在坐标系中作出∠AOB= 5π/3，易知：

如何求α角的三角函数值？

可借助解直角三角形求得琢终边与单位圆交点的坐标，再通过三角函数的定义求出琢的三角函数值。

例2：如图3，设α是一个任意角，它的终边上任意一点（不与原点O重合）的坐標为（x，y），点P原点的距离为r。求证：sinα= y/r，cosα= x/r，tanα= y/x。（检测学习目标5）

证明：如图4，设α的终边与单位圆交于点P0（x0，y 0），分别过点P，P0作x轴的垂线PM，P0M0，垂足分别为M，M0，则：

|P0M0| =| y0|，|PM|=| y |，|OM0 |=| x0 |，|OM |=| y0 |，△OMP ∽△OM0P0，所以：|P0M0|/1=|PM|/r ，即|y0|=|y|/r，因为y0和y同号，所以y0= y/r，所以sinα=y0= y/r；同理：cosα= x/r，tanα= y/x。

追问1：例2实际上给出了任意角三角函数的另外一种定义，而且这种定义与已有的定义是等价的，你能用严格的数学语言叙述一下这种定义吗？

一般地，对于任意角α，角α终边上任意一点P的坐标为（x，y ），它到原点O的距离为：

显然，任意角琢的三角函数值不会随终边上的点P的位置变化而变化。

5.引导学生进行课后反思

本节内容你获得的核心知识有哪些？能自主梳理出本节知识体系吗？你是通过什么方法和策略学会本节内容的？你觉得还有什么内容比较薄弱，需要老师提供何种帮助？你还有什么好的经验跟大家分享？

三、教材处理的探索

从教材的修订看，三角函数概念的教学经历了三个阶段：

第一阶段是由初中锐角三角函数引入，再在直角坐标系中研究锐角三角函数，用终边上的点的坐标比值定义三角函数。

第二阶段由初中锐角三角函数引入，再在直角坐标系中研究锐角三角函数，用终边与单位圆交点的横坐标及比值定义。

第三阶段是在单位圆中抽象对应关系，在函数概念指引下用终边与单位圆交点的横坐标及比值定义三角函数。

可以看出，数学核心概念的理解是循序渐进、逐步完善的过程。