智能车辆避障路径规划方法研究

赵 颖,张 琪,俞 庭,林先卬,张颖娟,李云伍,冀 杰

(1.西南大学 工程技术学院,重庆 400715;2.中国汽车工程学会,北京 100176)

随着无人驾驶技术的快速发展,路径规划与轨迹跟踪快速成为智能车辆的核心技术之一[1,2]。在车辆行驶过程中,采用合适的路径规划算法不仅能够安全、准确、快速地避障,且具有较高的乘坐舒适性,从而提高出行效率。

国内外学者已在路径规划与轨迹跟踪方面作了大量研究[3,4]。在避障路径的拟合方面,几何法和数值优化法的采用较为广泛。几何法是通过传感器获取障碍物的位置信息,从而生成多条无障碍几何曲线段,并在一定条件下连接形成避障代价最小路径的方法,多用于静态避障[5]。Liu等[6]通过分析直线路径上障碍物的位置信息,提出了一种由3段圆弧构成的小障碍物避障方法。刘宇峰等[7]通过传感器定位障碍物,结合拖拉机运动学模型规划避障圆弧,并采用分段圆弧连接的方法得到避障代价最小的路径。魏爽等[8]建立了基于预瞄点搜索的纯追踪模型,用于直线和曲线预设的局部跟踪路径规划。采用几何法进行避障路径规划简单、易实现,但在多段圆弧的连接处,路径曲率发生突变,引起原地转向现象,使得车辆转向稳定性降低。数值优化法是通过采用多项式函数,或插值函数生成多条曲率连续变化的曲线,并在一定条件下确定控制点,从而得到最优避障路径的方法。贝塞尔曲线和样条曲线的使用尤为广泛。Elhoseny等[9]提出了一种贝塞尔曲线与改进遗传算法相融合的方法,并对车辆进行了动态路径规划。余伶俐等[10]采用五次贝塞尔曲线平滑规划路径并进行多段曲线的光滑拼接,以曲线参数作为中间映射量,构建路径长度与轨迹坐标之间的状态映射模型,设计移动机器人的非时间运动参考量。李红洛等[11]设计了一种基于五阶贝塞尔曲线的前车换道路径规划方法。连建芳等[12]提出了一种基于三次样条插值的路径规划方法,并提出了一种新颖的混沌自适应粒子群优化算法来优化三次样条插值中的控制点。强宁等[13]提出了一种粒子群优法(Particle swarm optimization,PSO)算法与三次样条插值相融合的路径规划方法。于洋等[14]采用三次B样条曲线对无人车进行轨迹优化。夏晨等在静态突发威胁工况下,基于三次样条生成一系列候选路径。在动态突发威胁工况下,构建动态突发威胁相关模型,最终采用A*算法建立总代价函数,生成最优避障路径。

上述文献通过仿真分析方法验证了采用几何法或数值优化法进行避障路径规划的可行性,其中,几何法所规划的多为曲率不连续的路径,而贝塞尔曲线和样条曲线因其曲率连续的特性,可作为避障路径规划中的缓和曲线,使所规划的路径更平滑。对于以上两种常用的避障曲线,进一步比较两种曲线在车辆转向性能、驾驶稳定性、乘坐舒适性方面的优劣性,为后续开展车辆多种避障规划算法的融合具有一定指导意义。

基于此,本文针对五次贝塞尔曲线、三次贝塞尔曲线、五次样条曲线和三次样条曲线,进行避障路径规划研究,探究四种避障路径规划的特点及其工程实用性。首先,确定控制点并分别拟合出以上四种避障路径;其次,采用Matlab和Carsim联合仿真分析的方法对这四种避障路径的曲率进行对比分析;最后,基于无人驾驶试验平台,采用纯跟踪预瞄模型开展实车试验,以此对比探究四种避障路径的工程实用性,解决车辆在避障时由于路径曲率不连续易发生原地转向的问题。

1 避障路径规划

避障路径规划是根据工况设计可行的避障路径,并要求路径曲率连续,进而有效避免车辆在绕过障碍物时出现原地转向的现象,最终使车辆能够安全、快速、平稳地避过障碍物,继续行驶[16]。

1.1 贝塞尔曲线控制点

为简化计算,现以车辆避障的起始位置作为坐标原点,选取避障前半部分进行局部路径规划,如图1所示为避障路径规划示意图。

图1 避障路径规划示意图

贝塞尔曲线表达式[17]如下

(1)

(2)

式中：Pi代表控制点坐标,t代表参数,n为有理正整数。

五次贝塞尔曲线参数方程表示如下

P(t)=P0(1-t)5+5P1(1-t)4t+10P2(1-t)3t2+

10P3(1-t)2t3+5P4(1-t)t4+P5t5

(3)

曲线上任意点曲率[1]可表示如下

(4)

为获得五次贝塞尔曲线,需确定控制点坐标,基于贝塞尔曲线仿射变换的不变特性,首先,设定车辆在避障初始时刻的状态坐标

P0=(x0,y0)=(0,0)

(5)

设避障初始状态及最终状态车辆航向角均为0,则第二个控制点坐标P1(x1,0),设第三个控制点坐标P2(x2,y2)。根据式(4),当t=0时

(6)

求解得

(7)

基于五次贝塞尔曲线的避障路径如图2所示,其中,阴影部分代表障碍物,以车辆避障起点为P0,设障碍物的几何半径为R0,车宽为2w,车长为2l,对障碍物进行膨胀,膨胀宽度为车辆的几何半径ΔR

图2 基于五次贝塞尔曲线的避障路径

(8)

则膨胀后半径R可表达为

R=R0+ΔR

(9)

设第六个控制点状态坐标P5为

P5=(x5,y5)=(x5,R)

(10)

根据式(4)可求得

P3=(x3,y3)=

P4=(x4,y4)=(x4,R)

(11)

基于GILL P E提出的稳定序列二次规划(Stabilized sequential quadratic programming,SQP)算法[19],以路径平均曲率最小为目标,对参数x1、x2、x3、x4、x5进行优化。同理,限制避障路径的起点、终点和航线的连续性,选取图2中P0、P1、P4、P5四点,即可确定三次贝塞尔曲线。

1.2 样条曲线路径规划

图3为基于五次样条曲线的避障路径规划,以车辆避障初始点为原点,车辆纵向为X方向,车辆横向为Y方向建立坐标系。车辆在初始避障时的状态为Pstart,车辆在避障终点时的状态为Pend。

图3 基于三次样条曲线的避障路径

设避障路径为

P(s)=Pstart+s(Pend-Pstart)

(12)

式中：s=s(t),t∈[0,T],s∈[0,1],T表示整个避障过程所用的总时长。s的值域范围决定了该规划方式下的样条曲线的横向超调量始终为0,而若采用多项式函数规划样条曲线,将不可避免地产生横向超调量,故采取式(12)所示的样条路径,设五次样条曲线公式为

s(t)=b1t5+b2t4+b3t3+b4t2+b5t+b6

(13)

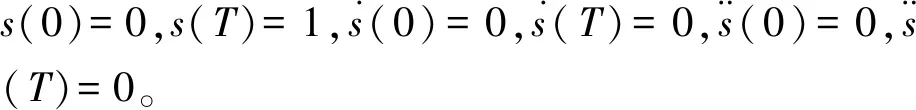
代入式(13),可求得

(14)

同理,可得三次样条曲线公式如下

(15)

2 仿真分析

在对本文所述两种避障曲线进行仿真前,首先对多项式函数规划的样条曲线,在不同始末距离前提下,选取四个控制点,拟合三次多项式样条曲线,避障曲线仿真结果如图4所示。

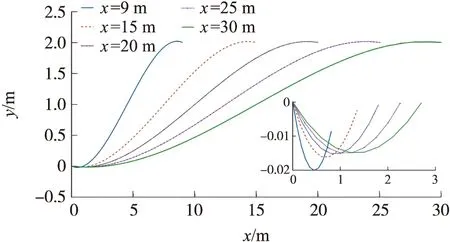
图4 不同始末距离的三次多项式样条曲线规划

由图4可知,其他条件一定时,三次多项式样条曲线存在一定的横向超调量,且始末距离越大,根据三次多项式拟合样条曲线的横向超调量越小。同理,五次多项式样条曲线及其它阶数的多项式样条曲线均存在横向超调量,而上文所提出的三次及五次样条曲线规划方法因其参数函数的值域范围特性,不存在横向超调量。故采用上文提出的三次及五次样条曲线规划进行仿真和试验分析。

图5为仿真环境下三次样条曲线、五次样条曲线、三次贝塞尔曲线和五次贝塞尔曲线的避障路径示意图。

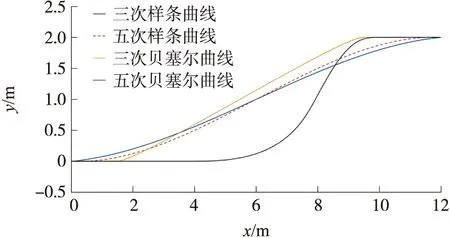
图5 避障路径示意图

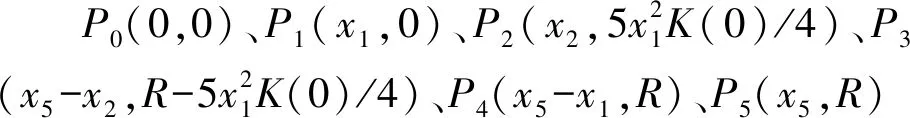
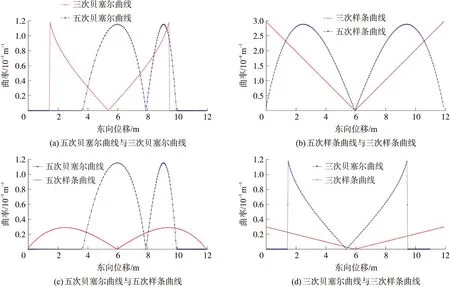
图6 四种避障路径曲线曲率对比

由图6(a)可知,三次贝塞尔曲线和五次贝塞尔曲线的曲率曲线均存在两个波峰和一个波谷,波峰处为车辆转向处路径的曲率变化,波谷的存在是由于车辆转向方向发生变化,路径曲率由1.176×10-6m-1(三次贝塞尔曲线),1.154×10-6m-1(五次贝塞尔曲线)逐渐降为0,再由0逐渐增大。三次贝塞尔曲线的曲率在两次波峰处发生突变,而五次贝塞尔曲线的曲率全程连续变化。由图6(b)可知,三次样条曲线和五次样条曲线的曲率曲线均存在两个波峰和一个波谷,波峰处为车辆转向处路径的曲率变化,波谷的存在是由于车辆转向方向发生变化,路径曲率分别由2.97×10-4m-1(三次样条曲线)、2.89×10-4m-1(五次样条曲线)逐渐降为0,再由0逐渐增大。由图6(c)可知,五次贝塞尔曲线曲率和五次样条曲线的曲率在避障全程中均不存在突变,变化连续且稳定,不产生原地转向现象,乘坐舒适性较好。由图6(d)可知,三次曲线的曲率存在突变,产生原地转向现象,乘坐舒适性较差。由此可见,不论是贝塞尔曲线还是样条曲线,三次曲线的曲率在换向处会发生突变,产生原地转向现象,乘坐舒适性较差,而五次曲线的曲率变化连续。综上,三次曲线比五次曲线的曲率波动幅度更大,曲率不连续引起原地转向,曲率变化率过大导致车辆的乘坐舒适性较差;五次曲线的曲率变化较稳定。

3 实车试验

为验证贝塞尔曲线和样条曲线在局部避障路径规划的工程实用性,选用搭载高精度GNSS/INS组合导航系统的无人驾驶平台进行试验,如图7所示。

图7 无人驾驶试验平台

图8 基于四种曲线的车辆横向加速度变化对比

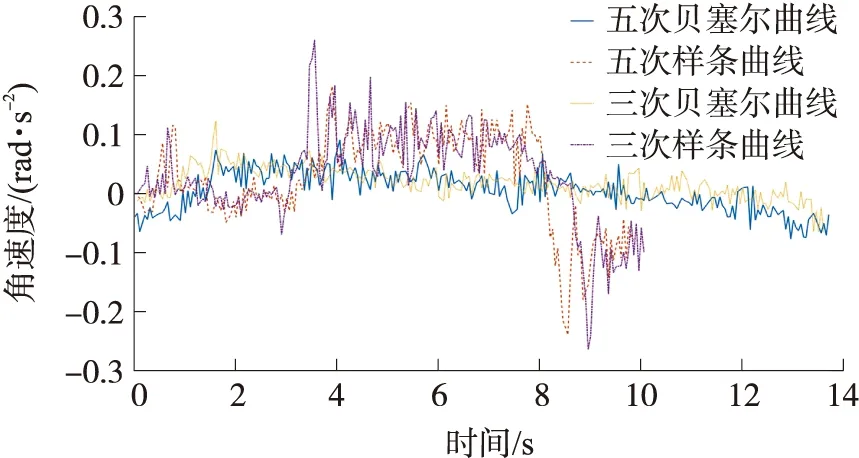
图9 基于四种曲线的车辆角速度变化对比

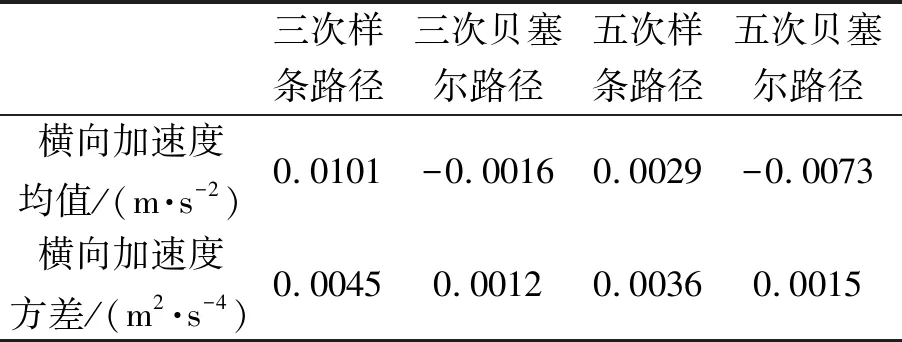
表1 两种避障轨迹下车辆横向加速度分析

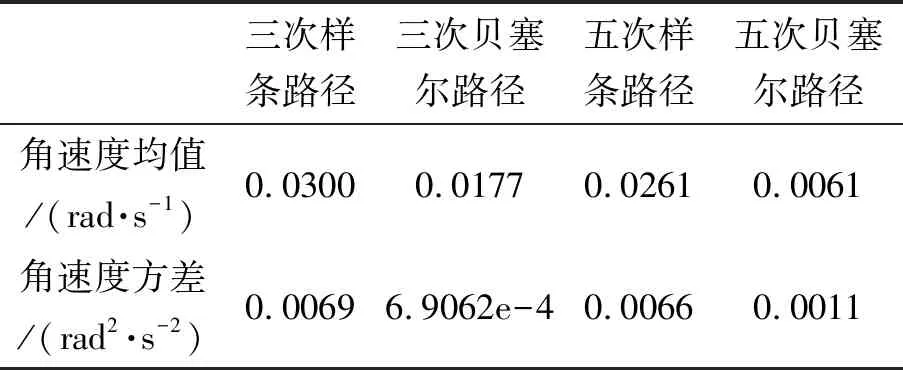
表2 两种避障轨迹下车辆角速度分析

从横向加速度指标分析,由表1可知,采用三次贝塞尔曲线时,车辆的横向加速度方差比采用三次样条曲线时减小73%,采用五次贝塞尔曲线时,车辆的横向加速度方差比采用五次样条曲线时减小58%。如图8所示,采用三次样条路径规划时,横向加速度均值最小,为-0.001 6 m/s2,采用三次样条路径规划时,横向加速度均值最大,为0.010 1 m/s2,采用三次和五次贝塞尔路径规划时,车辆的横向加速度方差均比采用三次和五次样条路径规划时车辆的横向加速度方差小。此外,采用贝塞尔曲线时,车辆横向加速度变化全程较稳定,而采用样条曲线时,车辆横向加速度在t=0和t=8.5 s处存在突变。因此,不论是三次曲线还是五次曲线,采用贝塞尔曲线时,车辆的横向控制比采用样条曲线时更加稳定。

从角速度指标分析,由表2可知,采用三次贝塞尔曲线时,车辆的角速度均值比采用三次样条曲线时减小41%,角速度方差比采用三次样条曲线时减小90%,采用五次贝塞尔曲线时,车辆的角速度均值比采用五次样条曲线时减小77%,角速度方差比采用三次样条曲线时减小83%;采用五次贝塞尔曲线时,车辆的角速度均值比采用三次贝塞尔曲线时减小66%,采用五次样条曲线时,车辆的角速度均值比采用五次样条曲线时减小13%。如图9所示,采用五次贝塞尔路径规划时,车辆角速度均值最小,为0.006 1 rad/s,采用三次样条路径规划时,车辆角速度均值最大,为0.030 0 rad/s。此外,采用不同阶数的同类曲线,车辆的角速度变化差异不大,转向性能均良好。进一步,不论是三次曲线还是五次曲线,采用贝塞尔曲线时,车辆角速度变化全程较稳定;采用样条曲线时,车辆角速度在t=4 s和t=9 s时存在突变,即车辆在转向时导致角速度变化幅度较大。

4 结束语

为解决车辆在避障时易发生的轨迹曲率不连续所导致的原地转向问题,本文选取三次贝塞尔曲线、三次样条曲线、五次贝塞尔曲线和五次样条曲线作为局部避障路径进行研究。通过Carsim与Matlab仿真软件对两种方法所得的轨迹及其曲率进行对比,并通过实车试验验证两种避障方法的相关技术指标,试验结果表明如下。

(1)由于样条曲线及贝塞尔曲线的数学特性,采用两类曲线进行避障路径规划,车辆的横向超调量均为0,车辆行驶平稳性较好。

(2)同类曲线中,三次曲线比五次曲线的曲率波动幅度更大,曲率不连续引起原地转向,曲率变化率过大导致车辆的乘坐舒适性较差。五次曲线的曲率变化较稳定;

(3)同阶数曲线中,采用三次贝塞尔曲线时,车辆的横向加速度方差比采用三次样条曲线时减小73%,采用五次贝塞尔曲线时,车辆的横向加速度方差比采用五次样条曲线时减小58%。因此,采用贝塞尔曲线进行避障路径规划时,车辆的乘坐舒适性更高。

(4)同阶数曲线中,采用三次贝塞尔曲线时,车辆的角速度均值比采用三次样条曲线时小41%,角速度方差比采用三次样条曲线时减小90%,采用五次贝塞尔曲线时,车辆的角速度均值比采用五次样条曲线时减小77%,角速度方差比采用三次样条曲线时减小83%。因此,采用贝塞尔曲线进行避障路径规划时,车辆的驾驶稳定性,及转向性能更加优越。