机场跑道内爆炸毁伤效应及工程化函数模型

胡榕, 姜春兰, 卢广照, 王在成, 毛亮

(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081; 2.中国兵器科学研究院, 北京 100089)

0 引言

对机场跑道进行高效毁伤,可有效阻滞敌机升空和返航,是现代战争夺取制空权的重要手段之一。目前反跑道弹药战斗部可分为动能侵彻战斗部和串联战斗部,无论何种类型战斗部,最终都是依靠弹体携带一定质量炸药至合适深度爆炸进而破坏跑道。因此系统研究装药对跑道的内爆毁伤效应,构建工程函数模型对于指导反跑道弹药的设计以及评估反跑道弹药的毁伤效应具有重要意义。

机场跑道一般由混凝土层、碎石基层、压实土层及地基等多层介质结构构成,装药在机场跑道内爆炸的毁伤机理和过程极其复杂[1-2],需要提取较多的毁伤效应参量描述,且大规模重复实验周期长、成本高。因此,国内外学者针对单层混凝土介质中的内埋爆炸进行了充分的研究[3-7],但对于多层介质中的内埋爆炸这一复杂问题研究得相对较少,一般采用数值仿真、小当量实验或少量全尺寸实验等方法,结合量纲分析研究跑道内爆炸毁伤相关问题。Westine[8]分析了混凝土/土复合介质内爆炸毁伤效应的关键影响因素,采用量纲分析法建立了经验公式。王清洁等[9]基于量纲分析通过拟合实验数据得到了爆炸漏斗坑的可见深度、实际半径与装药量关系的经验表达式。周宁等[10]分析了不同面层介质和不同深度下多层复合介质中爆炸产生的弹坑形状、体积及破坏面积,并结合实验数据得到了破坏参数与比炸深的无量纲关系式。江增荣等[11-12]针对侵爆战斗部对多层混凝土跑道的爆炸毁伤效应进行了研究,基于线性回归方法得到了装药量、炸点深度与炸坑面积之间的关系式。Hu等[13]开展了含铝炸药在机场跑道中爆炸毁伤实验,分析了不同装药埋深时面层混凝土的隆起高度。Wang等[14]从单层介质中成坑爆炸的相似律出发推导了双层介质中成坑爆炸的相似律,并根据相似准则设计缩比模型实验,得到了多层介质中爆炸成坑的基本规律。高一涵[15]通过数值模拟仿真研究了预制炮孔、装药量、炸点深度等对机场跑道爆炸毁伤效应的影响,并基于数值模拟结果,给出了毁伤半径与装药比例埋深的工程化表达式。

从现阶段研究状况和文献资料来看,部分学者基于量纲分析初步建立了理想炸药在机场跑道内毁伤效应的无量纲表达式,但对于机场跑道内爆毁伤场还未建立起规范统一的表征方法和较完善的工程函数模型及计算公式,尚不能对跑道弹坑形态、尺寸和裂纹特征等毁伤信息进行系统有效地表征,无法对毁伤效应进行有效地预测。

本文通过跑道内爆炸实验和大量数值仿真对机场跑道在装药内爆载荷作用下的毁伤效应开展了较系统深入的研究。基于实验获得的弹坑形态及裂纹破坏特征分析,提出采用敞坑、隆起和隐坑3种毁伤模式来描述毁伤场形态,通过毁伤模式和毁伤场特征参量来表征多层混凝土介质内爆毁伤效应的方法。基于量纲分析方法构建机场跑道内爆炸毁伤场特征参数工程化函数模型,通过实验与系统的仿真计算数据拟合得到跑道内爆炸毁伤场特征参数工程计算公式,对反跑道战斗部威力设计和毁伤效应评估具有重要参考意义。

1 研究方法

1.1 量纲分析

针对机场跑道内爆炸毁伤这一复杂问题,量纲分析是一个强有力的方法。机场跑道为面层混凝土、中间碎石层和压实土基组成的多层介质,应力波和爆轰产物都会与跑道各层介质相互作用,内爆炸毁伤过程极为复杂。运用量纲分析来处理机场跑道内爆炸毁伤这一复杂问题是一种非常有效的方法。与机场跑道内爆炸相关的变量主要可分为3部分:1) 炸药相关参数,装药量w、装药密度ρe、炸药爆热Qe、膨胀指数γ;2) 靶板材料相关参数,面层混凝土靶厚度hc、单块混凝土长宽lc、面层混凝土极限抗压强度σc、面层混凝土密度ρc、碎石层厚度hs、碎石层极限抗压强度σs、碎石层密度ρs、压实土层密度ρt、压实土层声速ct;3)交会参数,装药埋深h。

可运用上述参数进行量纲分析,以弹坑半径Rc为例,可写为

Rc=
f(w,ρe,Qe,γ,h,hc,lc,σc,ρc,hs,σs,ρs,ct,ρt)

(1)

选取w、Qe和h为基本量,按定理可写出无量纲关系式:

(2)

不考虑装药密度等常数,在面层、碎石层以及压实土基各层强度不变的条件下,式(2)可简化为

(3)

同理,其他毁伤参量可以以w、Qe和h为基本量转换。

由此,机场跑道内爆炸毁伤场参数主要涉及的装药埋深h和装药量w两个关键因素,在实验与仿真方案中也主要针对装药埋深h和装药量w开展相关研究。

1.2 机场跑道内爆炸实验方案

靶标单块尺寸为5 m×5 m,由40 cm厚混凝土面层、40 cm厚中间碎石层、40 cm厚压实土层和自然土基组成,根据国家军用标准GJB 1278—1991要求修筑机场跑道靶标,为避免边界效应影响,采用多块靶标连片修筑,边缘加修1.5 m的边界靶。面层混凝土的成分质量配比为水泥∶砂∶碎石∶水=356∶1 032∶848∶178,混凝土养护28 d龄期抗折强度不低于5 MPa。碎石中间层采用级配的方式,最大粒径不超过4 cm,压实土层为沙土,采用机械压实,压实度为95%。

药柱质量由实验方案给出,实验时将裸装药柱置于指定装药埋深后,用土壤填充剩余预留弹孔。在靶标外安全距离处放置高速摄影系统,捕捉靶板隆起抛掷过程,实验设置如图1所示。

图1 靶标修筑及实验布置示意图Fig.1 Schematic diagram of runway targets and test layout

从反跑道子弹药设计需求出发,优选4种装药量(2 kg、3 kg、4 kg和5 kg)。一般对于跑道内爆炸而言,在碎石层或者土层中爆炸时其毁伤效果最好[16],由此设置装药埋深由碎石层上部至土壤层,每种装药量选择4种埋深(43 cm、53 cm、63 cm和73 cm)进行实验,共计进行16组实验以研究不同装药量和装药埋深对跑道爆炸毁伤效应的影响。

1.3 机场跑道内爆炸数值仿真模型

为得到机场跑道内爆毁伤破坏的详细过程以及获得更加系统、全面的跑道内爆毁伤数据,采用数值仿真方法对不同药量TNT装药在跑道内不同埋深下的爆炸毁伤效应进行了数值模拟研究。

根据跑道结构的对称性,为提高计算效率,建立三维1/4仿真计算模型,如图2所示。仿真数值模型参照实验状态设置,其中面层厚度40 cm,碎石层为40 cm,压实土层为120 cm,考虑实验中为带有边界靶的连片混凝土跑道靶标,因此设置宽度为 1.5 m 的边界靶。装药选用TNT装药,位于靶板中心位置,不同工况下的弹孔均用土壤填充。采用多物质Euler与Lagrange耦合算法,其中面层混凝土和碎石层采用Lagrange网格。

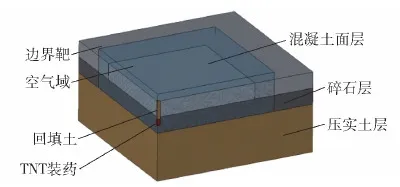
图2 1/4计算模型Fig.2 1/4 finite element model

在机场跑道内爆炸毁伤实验的基础上,通过数值仿真扩充埋深工况。与实验相对应,仿真模拟 4种装药量(2 kg、3 kg、4 kg和5 kg)在全尺寸四级跑道内不同装药埋深下的毁伤效果,仿真工况中装药埋深分别为48 cm、58 cm、68 cm、78 cm、88 cm和98 cm,共计24组工况。

1.4 材料参数标定

材料模型及参数是影响数值仿真结果最主要的因素之一,仿真中碎石层材料抗压强度为8 MPa[17]。压实土层采用带失效的土壤与泡沫材料模型[18]。TNT炸药采用High_Explosive_Burn材料模型和JWL状态方程描述[19]。考虑到面层混凝土介质在装药爆炸作用下,其破坏形式主要是受到拉伸波的作用剪切破坏断裂,因此仿真中通过用户自定义模型材料接口将TCK模型嵌入LS-DYNA软件中,采用能反映拉伸失效的TCK模型来描述面层混凝土在爆炸加载下的动态响应过程。

为验证模型参数并对参数调试提供依据,按照1.1节中的实验方法进行3组机场跑道内爆炸毁伤实验,标定实验方案列于表1。开展对应工况的数值仿真,通过对比实验数据与仿真结果,标定混凝土材料参数,标定后的混凝土材料参数列于表2。

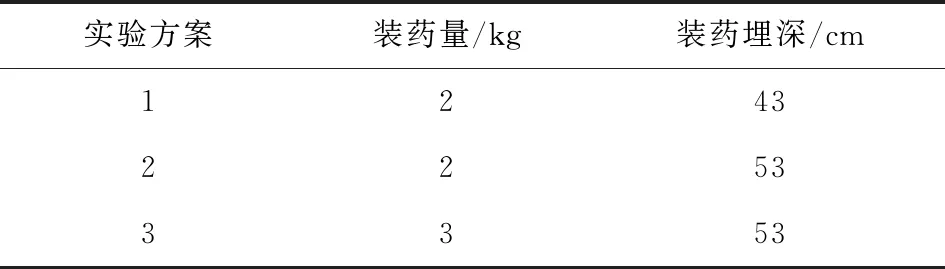
表1 材料参数标定实验方案

表2 混凝土材料参数

参数标定实验结果和仿真结果如表3所示。仿真和实验的毁伤形态一致,裂纹数量与走向一致,内部裂纹分布也比较合理,毁伤场参量较为接近。因此,本文采用的算法、材料模型及参数能够反映实际爆炸情况,可有效模拟真实装药在跑道内的爆炸毁伤效应。

表3 参数标定实验与仿真毁伤效果对比

2 结果与分析

2.1 实验及仿真结果

2.1.1 典型内爆炸毁伤过程

开展1.1节中的16组机场跑道内爆炸毁伤实验,并采用经过校验的数值模型进行24组工况仿真计算,共计得到40组TNT装药在机场跑道内爆炸毁伤结果。

高速摄像机拍摄到的典型跑道内爆炸毁伤过程如图3(装药量4 kg,装药埋深53 cm)所示,同时进行对应的数值仿真,得到靶板内部爆炸过程仿真结果,见图4。结合高速摄像机照片和仿真结果,可以清楚地看出装药在机场跑道内爆炸后混凝土破碎、抛掷的过程。装药在跑道中爆炸时,装药正上方混凝土先破碎,破碎的混凝土和填充土很快喷出,随后面层混凝土产生径向裂纹、环向裂纹和鼓包,鼓包速度在很短时间内达到最大值;随后在爆轰产物的作用下裂纹迅速拓展,互相贯穿,随着爆轰产物的进一步膨胀,混凝土碎块被抛掷出去形成弹坑。

图3 跑道内爆炸典型毁伤过程实验结果 (装药量4 kg,装药埋深53 cm)Fig.3 Typical damage process of internal explosion of a runway (4 kg TNT with 53 cm buried depth)

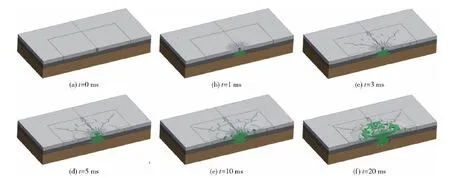
图4 跑道内爆炸典型毁伤过程仿真结果 (装药量4 kg,装药埋深53 cm)Fig.4 Typical damage process of implosion of runways in simulation (4 kg TNT with 53 cm buried depth)

2.1.2 机场跑道内爆炸毁伤场

表4为16组跑道内爆炸实验结果照片。对所有实验工况得到的机场跑道毁伤结果进行对比分析可以发现,多层介质跑道在内爆炸载荷作用下,会出现抛掷型弹坑、表面隆起以及地下隐坑这3种主要的宏观弹坑形态,其中混凝土面层还会出现径向裂纹、环向裂纹和崩落等毁伤形式。当装药量一定时,随装药埋深的增加,跑道的毁伤模式由敞坑变为隆起最后变为隐坑模式;当装药埋深一定时,随着装药量的变大,炸药爆炸释放的能量越来越多,机场跑道的毁伤模式经历从隐坑到隆起再到敞坑模式的转变,跑道毁伤面积逐渐增大。

目前文献中针对机场跑道内爆毁伤场的表征没有统一的标准[8,20-23]。对于毁伤跑道而言,一般认为敞坑型破坏和隐坑破坏是比较好修复的,只需要把空洞填满,然后铺上钢板就能起降飞机了。而当面层混凝土形成隆起破坏时,在修复跑道需要在填充弹坑之前先把弹坑周围的混凝土去掉或者弄平整,在修复上难度最大。为了更好地判断机场跑道内爆炸毁伤效果,本文采用毁伤模式和毁伤场特征参量相结合的方法对机场跑道内爆毁伤场进行表征,使机场跑道内爆毁伤效果的表述更加清晰规范。其中,跑道毁伤模式可结合跑道弹坑形态和裂纹类型划分为敞坑模式、隆起模式和隐坑模式,如图5所示。毁伤场特征参数分别为弹坑半径Rc、有效毁伤半径Red、爆腔半径Ric和弹坑深度H,毁伤参量测量示意图如图6所示。

需要说明的是,各种毁伤模式界面并不十分明显,为了便于区分,参考机场跑道道面平整度标准[24],当道面高差达到30 mm时平整度较差,跑道无法使用,需立即进行修复。当面层混凝土隆起高度达到30 mm时,为隆起模式;对应当隆起高度小

表4 跑道内爆炸实验结果

图5 跑道内爆炸毁伤模式Fig.5 Damage modes of the implosion of runways

图6 跑道内爆炸毁伤场特征参数Fig.6 Damage parameters of the implosion of runways

于30 mm且未形成环向裂纹时,为隐坑模式。

2.1.3 实验与仿真结果

按照图5测量所有实验与仿真工况的毁伤参量及毁伤模式结果,统一列于表5。

2.2 机场跑道内爆炸毁伤模式

机场跑道内部爆炸毁伤,本质上是混凝土-碎石-土壤3层介质的爆炸毁伤问题,其中对机场跑道毁伤模式起决定性作用的是面层混凝土的毁伤结果。因此提取典型工况下(4 kg装药,53 cm装药埋深,与2.1.1节一致)面层混凝土的应力数据,讨论机场跑道的破坏模式,如图7所示。

装药在跑道内起爆后,爆炸冲击波传入周围介质,由于面层混凝土介质波阻抗大于基层介质,故当冲击波从基层传向面层时,将向面层透射一个峰值减弱的压缩波,并向自由表面继续传播。压力峰值迅速衰减,不足以粉碎毁伤上层混凝土,但对于混凝土介质而言,其抗拉强度仅为抗压强度的1/8[10],因此应力波传播到自由面反射成的拉伸应力波仍能使混凝土表面产生层裂现象和裂纹,如图7中1 ms时刻,装药上方的混凝土介质面层出现层裂破坏。

面层混凝土在拉伸应力波的作用下产生向外的径向位移,从而产生拉应力,当拉应力大于混凝土抗拉强度时,混凝土被拉断,产生径向裂纹;混凝土介质在压缩波作用下积蓄弹性变形能,而后在稀疏波作用下,弹性势能释放,形成与压缩波方向相反的向心拉应力,如图7中3 ms时刻应力云图,当拉应力大于介质抗拉强度时,产生环向裂纹,如图4中5 ms时刻图像。随后环向裂纹和径向裂纹贯通形成破碎区。由于爆轰产物的飞散受到面层混凝土的阻拦,高温高压的气体渗入混凝土-碎石层界面,推动面层混凝土向上运动,径向裂纹得以扩展至靶板边界,面层混凝土沿环向裂纹向上运动,在环向裂纹处向上隆起,最终形成带有径向和环向裂纹的隆起模式毁伤区。这也说明了装药爆炸后传入混凝土中的爆炸应力波大小决定了混凝土面层径向和环向裂纹的生成,爆轰气体产物的膨胀做功能力决定了裂纹的进一步扩展延伸的程度。

这也解释了表4中的实验结果。当装药埋深较浅时,炸药能量很快扩散至空气中,在面层混凝土形成较小的敞坑以及径向和环向裂纹,形成敞坑模式;当装药埋深继续增加,传递给机场跑道的能量增加,

表5 不同装药埋深下的毁伤参量及毁伤模式

图7 面层混凝土应力 (装药量4 kg,装药埋深53 cm)Fig.7 Simulation results of xy stress of topping concrete (4 kg TNT with 53 cm buried depth)

除了在面层形成径向和环形裂纹,爆轰产物膨胀还会推动混凝土层介质沿最小抵抗线向上运动,在环向裂纹处向上隆起,形成隆起模式;当装药埋深继续增大,在压实土层爆炸时,爆炸应力波在土壤中的传播性能较差,传播速度也较低,爆炸应力波对面层的作用效果已不明显,面层混凝土仅在反射拉伸应力波的作用下发生较小的层裂,爆炸能量更多向地下耦合,形成隐坑模式。当装药埋深一定时,随着装药量的变大,炸药爆炸释放的能量越来越多,冲击波压力峰值增大,爆轰气体增加,冲击波和爆轰气体对机场跑道多层介质的作用明显增强,跑道毁伤面积逐渐增大。

3 机场跑道内爆炸毁伤工程函数模型

3.1 机场跑道内爆毁伤模式判断

对于反跑道弹药而言,毁伤跑道时形成隆起模式造成的修复难度大、修复时间长,可对跑道形成相对较长时间的封锁,达到较佳的毁伤效果。因此,预估机场跑道的毁伤模式对于设计得到具有最佳毁伤效能的反跑道弹药具有重要价值。

参考利文斯顿提出的以能量平衡为准则的岩石破碎的爆破漏斗理论[25],从能量的角度出发,在机场跑道条件与装药一致的情况下,爆破能量的多少取决于有效炸药能量的多少。而与有效炸药能量相关的参数除了装药量,还有装药埋深。装药埋深越浅越接近地表爆炸,传递给机场跑道的能量比例相应减少,而传播给空气的能量比例相对增加。因此,根据前面的实验和仿真结果绘出不同药量与不同埋深机场跑道爆炸破坏模式图,如图8所示。

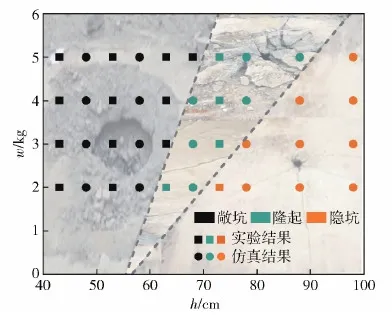
图8 不同装药量和装药埋深下的毁伤模式Fig.8 Damage modes with different charge quantity and buried depth levels

图8中的跑道破坏模式明显是线性可分的,可以划分为3个区域。支持向量机(Support Vector Machines, SVM)是当前应用最广泛的分类方法[26-27],通过支持向量机对数据进行分类。在二维空间内使用线性核函数进行分类,得到机场跑道内爆炸毁伤模式的决策函数为

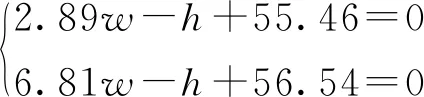
(4)

当2.89w-h+55.46>0时,跑道的内爆炸毁伤模式为敞坑模式;当2.89w-h+55.46<0且6.81w-h+56.54>0时,跑道的内爆炸毁伤模式为隆起模式;当6.81w-h+56.54<0时,跑道的内爆炸毁伤模式为隐坑模式。

3.2 机场跑道内爆炸毁伤场特征参量的拟合关系式

本文中,主要讨论内爆毁伤场参数涉及的装药埋深h和装药量w两个主要影响因素。将式(3)中的f1展开为级数形式并取前4项为

(5)

式中:ai为待定系数,i=0,1,2,3。

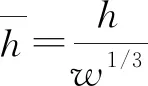
(6)

(7)

(8)

(9)

拟合曲线如图9所示。由此得到机场跑道内爆毁伤场特征参量的工程化函数模型,该模型适用于装药w1/3/h在1.3～4.0之间,装药长径比小于2,面层混凝土厚度为40 cm,强度约40～50 MPa的情况下。从而可基于装药量和装药埋深预测装药在跑道内爆炸的毁伤模式与毁伤场特征参量,评估反跑道弹药的毁伤效果,也可用于指导反跑道弹药的设计。

4 结论

本文针对反跑道弹药战斗部对机场跑道内爆毁伤效应评估的需求,开展了不同装药质量、不同装药埋深下的机场跑道内爆毁伤实验和数值仿真研究,获得了不同装药条件对跑道毁伤动态响应和弹坑形态的影响规律。得出主要结论如下:

1)机场跑道为面层混凝土、中间碎石层和压实土基组成的多层混凝土介质,应力波和爆轰产物都会与跑道各层介质相互作用,内爆炸毁伤过程极为复杂。基于实验获得的弹坑形态及裂纹破坏特征分析,提出采用毁伤模式和毁伤场特征参量相结合的方法,将机场跑道的毁伤模式分为3类:敞坑模式、隆起模式和隐坑模式;采用毁伤场特征参量弹坑半径Rc、有效毁伤半径Red、最大爆腔半径Ric,以及弹坑深度H对跑道内爆毁伤场形态进行定量描述,能够有效表征机场跑道内爆毁伤场。

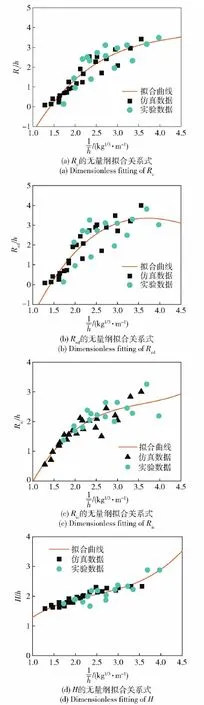
图9 无量纲毁伤参数拟合曲线Fig.9 Fitting curve of dimensionless damage field parameters

2)跑道毁伤模式与装药质量以及埋填条件相关,可通过控制药量和埋深,使跑道出现不同毁伤模式。装药量一定时,有效毁伤半径Red随装药埋深的增加呈先增大后减小的趋势。装药埋深一定时,毁伤效应参量随装药量的增加而增大,炸药爆炸能量和装药埋深的最适匹配才能达到理想的毁伤效果。实验和仿真结果表明,在本文所研究的工况条件下,装药质心在碎石层中部左右能实现最大有效毁伤半径。

3)结合大量仿真和实验数据拟合得到机场跑道内爆毁伤模式和毁伤场场特征参量的工程化函数模型,从而可基于装药量和装药埋深预测装药在跑道内爆炸的毁伤模式与毁伤场参量,可为反跑道战斗部设计和威力评估提供参考。