基于预定毁伤概率的悬浮式深弹使用方法
吴玲, 王丕琨, 卢发兴
(海军工程大学, 湖北 武汉 430033)
0 引言
随着鱼雷技术的发展,现代潜射鱼雷对水面舰艇的威胁越来越大[1-2]。传统鱼雷对抗措施[3-10]难以满足舰艇对抗鱼雷的需求,其主要原因是声呐只能测定来袭鱼雷方位变化信息,而其距离测量量误差较大。为提升对鱼雷毁伤概率,采取区域射击方式[11],在鱼雷可能航路上布设深弹拦截线方法逐渐成为研究热点。如俄罗斯的“蟒蛇”反鱼雷系统利用估计距离和方位,在鱼雷的可能航向上布设一个带声呐探测装置的悬浮深弹阵,增强对鱼雷的毁伤概率[12]。
由于舰艇携带深弹数量有限,在达到既定毁伤概率的前提下合理确定深弹布设密度成为这一问题关键。现有文献[13-19]主要通过布设线长与深弹毁伤半径比来确定布设数量,再通过乘以比例系数调整布设数量,改变毁伤概率,无法根据既定概率快速求解布设密度,且没有考虑深弹布设本身存在的误差,所求初值距真值差距较大。
为解决基于既定概率配置深弹数量这一问题,本文通过构建最优中间函数[20],利用条件极值计算深弹均匀配置模型下的理论最优毁伤概率解析解。根据最优毁伤概率,构建初值函数,确定深弹配置数量初值,通过迭代计算既定概率下深弹配置数量。进一步,依据深弹作战使用方法,确定区域射击范围和深弹实际配置方法。相比传统方法,采取本文方法确定的深弹布设数量初值与真值接近,经过较少迭代次数即可求解真值,且通过对初值的修正,可以达到快速求解计算的目的,节省了求解时间,提升了求解精度。
1 基于区域射击的深弹毁伤鱼雷概率模型
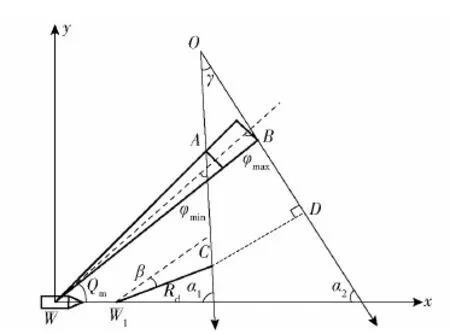
建立l坐标轴,使之垂直于鱼雷的期望航路,期望航路与坐标轴的交于原点O(见图1)。图1中αi为第i枚深弹射线与拦截线的夹角,lx为鱼雷航路最可能分布的区间半径。

图1 区域射击拦截鱼雷示意图Fig.1 Diagram of torpedo-intercepting shooting area
由于鱼雷发射距离较远,且对其定位精度有限,认为其在(-lx,lx)区间内服从均匀分布。悬浮式深弹杀伤半径为Rd,认为鱼雷在半径内即被毁伤。
火箭深弹在其射击坐标系上的距离和方向误差对应的标准差分别为σd、σβ(对应的概率误差为Ed、Eβ),其在l轴上的投影分别为
(1)

(2)
ξxi为第i发深弹的瞄准点坐标。当鱼雷经过l轴坐标为x时,第i发火箭深弹毁伤概率为
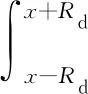
(3)
式中:xa为第i发火箭深弹实际的布设坐标。考虑所有鱼雷所有可能经过点,其毁伤概率为
(4)
式中:f(·)为关于鱼雷经过拦截线某一位置的概率密度函数。鱼雷经过拦截线某一位置这一事件服从均匀分布,因此第i发深弹对鱼雷的毁伤概率为
(5)
为减小计算量和求解难度,深弹采取均匀布设方式。每个提前点布置1发深弹,由于每一发深弹的误差投影角αi不同,因此每一发深弹在l轴服从不同概率误差的正态分布,概率误差为
(6)
当鱼雷从l轴上x点经过时,其至少被一发深弹所毁伤的条件概率为
(7)
pi(|x-ξxi|)为当系统误差为某一固定偏差值|x-ξxi|时,第i发深弹在此系统偏差下毁伤鱼雷的条件概率,
(8)
考虑鱼雷所有可能经过位置,其毁伤概率为
(9)
2 最优毁伤概率求解
求解鱼雷被毁伤的最大概率,等同于求解鱼雷未被毁伤的最小概率:
(10)
引入射弹散布密度函数:
(11)
则鱼雷被毁伤概率变式为

(12)
显然U在(-∞,∞)上的积分与瞄准点位置ξxi无关,构造τ:
(13)
将式(13)作为等周条件,通过变分法求解最优U以及对应的最优毁伤概率P,此时目标函数变换为
I=f(x)e-U+λU
(14)
式中:λ为引入的待优化宗量。由于f(x)服从均匀分布,其在-lx、lx两点不连续,将其延拓为2阶连续函数以进行变分法求解,其延拓函数为
(15)
式中:φ1(x)∈C2(-lx-δ,-lx+δ),δ为一无穷小量,且
(16)
φ2(x)∈C2(lx-δ,lx+δ),且
(17)
因此有
(18)
以f*(x)代替f(x)得到I*,根据欧拉-拉格朗日条件,U的最优值U0应为
(19)
的解,即U0应使得
-f*(x)e-U0+λ=0
(20)
代入式(13),可得
(21)
因为当x∉[-lx,lx]时,射弹散布对于目标的毁伤无影响,因此式(21)变换为
(22)
解得
(23)
代入式(20),有
(24)
在x∈[-lx,lx]时,最优解同样满足:
-f(x)e-U0+λ=0
(25)
对U0(x)最优性进行证明,假设存在最优函数:
U1=U0+η(x)
(26)

显然,U1满足:
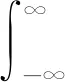
(27)
且有

(28)
证明式(20)最优,即证明

(29)

由基本不等式1-e-x≤x,可得

(30)
因此

(31)
即证明U0是使P0最大的函数。因此得到最优毁伤概率:
(32)
3 基于预定毁伤概率求解布设数量
当确定毁伤概率Pc、误差条件和配置方法,因此影响毁伤概率只有深弹数量n。传统方法通过拦截区间长度与杀伤半径的比值来确定布设深弹数目:
(33)
式中:kp为比例系数,kp∈+。此方法无法直接根据预设概率Pc求取布设弹数n,只能通过逆向枚举计算求取符合概率Pc的布设弹数n。无法直接根据预定毁伤概率确定初值,求解时间不稳定。
为解决此问题,本文提出基于预定毁伤概率的布设密度求解公式。将毁伤概率表示为关于布设深弹数量的函数P(n),布设深弹数量求解问题转化为优化问题:

(34)
对于深弹数量n,引入序列nk,有
(35)
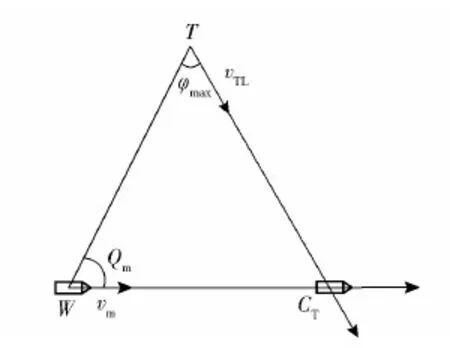
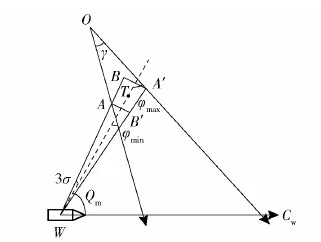
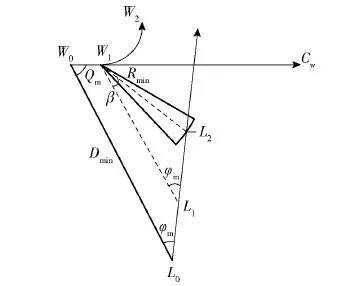
式中:φ(Pc)为初值计算函数;ϑ(nk)为布设深弹数量计算迭代函数。迭代终止条件为|nk-nk-1|<1。首先通过初值函数φ(Pc)计算深弹数量初值n1,通过计算迭代函数ϑ(nk)迭代,逼近真实值n∞。为使迭代过程在满足终止条件时有P(nk)≥Pc,需要使P(nk) ϑ(nk)-nk>1 (36) 求解布设深弹数量,首先构建初值函数。为了减少运算复杂度,遵从保守原则,选取散布最大的提前点散布参数Emax作为所有提前点的散布参数。 构造τ′、τ: (37) 由式(37)可得 n=-2lxln (1-P0)/τ′ (38) 从而有 n0=φ(Pc)=-2lxln (1-Pc)/τ′ (39) 通过迭代法求解: (40) (41) 结合式(40),可得 nk+1=ϑ(nk)= (42) 式中: (43) 求取预定毁伤概率下的布设深弹数量,需要计算拦截区间。根据实际作战使用情况和鱼雷航路张角确定鱼雷可能航路区间(-lx,lx),确定深弹布设方案。 假设某一时刻t0发出鱼雷报警信号,根据鱼雷与舰艇解相遇原理,满足 vmsinQm=vTLsinφ (44) 式中:vm为目标舰艇速度;Qm为发现鱼雷的舷角;vTL为鱼雷运动速度;φ为鱼雷攻击提前角。 图2为最大提前角射击示意图。图3为最小提前角射击示意图。图2和图3中,T为鱼雷发射点,W为鱼雷发射时刻我舰艇位置,CT为鱼雷与我舰艇相遇位置,φmax为最大攻击提前角,Ds为深弹发射的期望距离,L为尾流长度,Q′为鱼雷攻击尾流时的最大敌舷角,φ′ 为最大提前角与最小提前角的差角。 图2 最大提前角射击示意图Fig.2 Firing at the maximum advance angle 图3 最小提前角射击示意图Fig.3 Firing of the minimum advance angle 在同一攻击态势下,鱼雷攻击提前角与鱼雷种类有关:直航鱼雷攻击提前角最大,尾流制导鱼雷攻击提前角最小。当鱼雷为直航鱼雷时,根据式(44),其攻击提前角为 (45) 当鱼雷为尾流制导鱼雷时,其攻击提前角使得鱼雷与舰艇尾流相遇并进入尾流。通常,尾流长度为 L=180vm (46) (47) 设Qm-φ′=Q′,有 (48) 图4 确定航路张角示意图Fig.4 Range of possible routes 图4为确定航路张角示意图,图中Cw为我舰航向。当声呐通过被动方式探测到鱼雷T,只能获取其方位信息,其距离信息依靠估计获取。声呐探测角误差为σ,则鱼雷最可能存在区域为AA′BB′。为覆盖鱼雷所有可能经过区域,在A点选取最小攻击提前角,在B点选取最大攻击提前角,则γ为鱼雷航向张角。 当鱼雷告警紧急时,必须在鱼雷到达深弹射击近界之前将拦截线布设完成。图5为紧急条件射击态势图,Rmin为深弹发射近界,φm为在紧急条件射击态势下的鱼雷攻击提前角,β为深弹发射提前角。 图5 紧急条件射击态势图Fig.5 Firing under emergency conditions t0时刻舰艇所处位置为W0,鱼雷位于L0,收到鱼雷报警信息。经过最短准备时间trmin后,舰艇于W1处发射深弹,并进行机动规避,此时鱼雷位置为L1,深弹从发射到进入工作状态需要经历飞行时间tf和水下准备时间tc。深弹布设完毕后鱼雷恰好到达L2。 根据深弹解相遇原理: (49) Dmin=Rdcosβ+vTL(tf+tc+trmin)cosφM+vmcosQm (50) 式中:Dmin为最小发现距离。 由于情况紧急,需要从近点C选择最短的拦截线开始布设。已知发射深弹时舰艇位置W1(vwtr,0 m),vw为我舰艇航速,tr为深弹准备时间,求取C点坐标: (51) 已知: (52) 式中:Kds为距离误差系数,则发现距离范围为[(1-Kds)Ds,(1+Kds)Ds]。图6为紧急条件区域拦截示意图,α1、α2分别为最大、最小攻击提前角时鱼雷航向与我舰航向夹角。 图6 紧急条件区域拦截示意图Fig.6 Diagram of area interception under emergency conditions 由 (53) 确定O点坐标(xO,yO)。由 (54) 确定D点坐标(xD,yD)。 当鱼雷在深弹射程之外被发现时,将深弹布设于最大射程处。为最大范围覆盖鱼雷航向张角,选取拦截线垂直于航向张角角平分线。图7为正常条件区域拦截示意图。 图7 正常条件区域拦截示意图Fig.7 Diagram of area interception under normal conditions 已知W1(vwtr,0 m),求取F(xF,yF)为布设基准点: (55) 式中:xW1、yW1分别为图7中W1点的横、纵坐标。 拦截线长度为 (56) 在拦截线长度2lx和布设数量n已知的条件下,深弹布设的瞄准点也得以确定:以间距为2lx/n均匀布设在拦截线上。 想定条件:某舰艇以30 kn航速航行。于t0时刻接收到鱼雷报警,报警信号来自左舷60°,估计距离5 km,声呐角误差σ为0.02 rad,距离误差系数Kds为0.02,估计鱼雷航速44 kn。舰艇准备利用深弹进行区域拦截射击,最快准备时间trmin为20 s。深弹射击远界Rmax为3 000 m,将深弹布置于最大射程处。根据式(55)、式(56),算得深弹布设中心点坐标(2 181 m,2 337 m)和拦截线长度2lx=1 473 m,绘出深弹拦截态势图(见图8)深弹毁伤半径Rd=30 m,射击方向误差Eβ=30 m,距离误差Ed=20 m,基于预定毁伤概率Pc=0.6对所需要发射弹数进行仿真计算,得到计算结果(见表1)。 图8 深弹区域拦截示意图Fig.8 Diagram of area interception of a deep bomb 表1 两方法计算结果对比 基于算例的想定条件,改变射击误差Eβ、Ed,计算当射击误差Eβ、Ed分别取较小、适中和较大值时,本文方法和传统方法的计算结果(见表2)。 表2 不同射击误差条件计算结果比较 改变声呐探测角误差σ和距离误差系数Kds,根据式(55)、式(56),计算出不同的布设基点和拦截线长度。基于不同拦截线长度,在Eβ=30 m、Ed=20 m条件下,对比本文方法确定初值与传统方法确定初值的精度(见表3)。 表3 不同声呐精度下计算结果比较 通过仿真计算可知: 1)通过表1对比,本文提出的方法能够直接基于预定毁伤概率得出与精确结果相近的计算初值。只需经过较少次数迭代,便可获得精确计算结果。而传统方法无法根据预定毁伤概率计算深弹布设数量。 2)通过表2对比,传统方法计算布设密度,一方面没有考虑预定毁伤概率,另一方面,没有考虑射击误差。这使得在不同射击误差下,传统方法确定的布设密度难以达到预期的毁伤效果。本文提出的方法保证初值精度的同时,计算耗时短,实用性强。 3)由表2、表3可以发现,本文提出的方法初值与精确计算结果误差不超过2,因此为了节省计算时间,可以通过对初值计算进行修正,以获取近似计算结果。对式(39)进行修正: n′0=-2lxln (1-Pc)/τ′+2 (58) 式中:n′0为布设深弹数量的近似计算结果。 随着深弹区域射击在反潜中应用的推广,在有限的载弹条件下尽可能合理发挥深弹毁伤来袭鱼雷的效率,拦截尽可能多批次鱼雷的袭击,对于提升舰艇生存概率具有重要意义。本文提出的基于既定概率深弹配置数量计算方法以及具有时效性的近似计算方法,能够在既定作战需求下,准确地计算深弹配置数量,避免传统反潜过程中为保证舰艇生存概率而大批量使用深弹拦截单一批次鱼雷,使得舰艇能够在有限载弹条件下提高拦截鱼雷批次数量,提升舰艇生存概率。且本文提出的近似计算方法在保证精度的前提下,极大地减少了计算耗时,保证了时效性,具有实际使用价值。为后续反潜作战深弹战法运用提供了一定理论基础。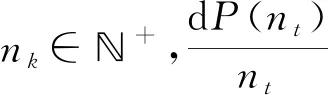
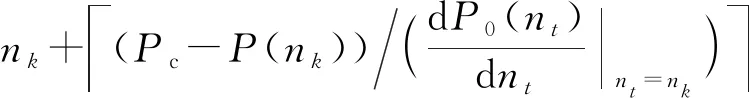
4 确定深弹拦截线


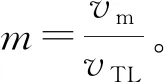
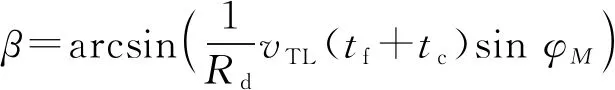

5 仿真计算




6 结论

