一维慢速烤燃模型点火点位置及其温度的理论计算

张坤, 智小琦, 肖游, 王帅

(1.中北大学 机电工程学院, 山西 太原 030051;2.中国兵器装备集团自动化研究所有限公司 智能制造事业部, 四川 绵阳 621000;3.湖北航天化学技术研究所 航天化学动力技术重点实验室, 湖北 襄阳 441003)

0 引言

研究弹药在热环境中的响应特性对弹药在寿命期的安全使用具有重要意义。因为弹药无论是受热刺激、强电磁辐射或二者的综合作用,最终导致弹药响应的均是因含能材料受热后的自持反应所致。目前,模拟弹药受热刺激作用的研究方法主要是快速烤燃和慢速烤燃。快速烤燃模拟弹药在大火作用下的响应特性,慢速烤燃模拟弹药在暗火作用下的响应特性。研究手段主要采用试验和仿真技术。试验方法主要采用北大西洋公约组织标准化协定STANAG 4240(快速烤燃试验)和STANAG 4382(慢速烤燃试验),试验研究内容包括弹药尺寸[1-2]、约束条件[3-4]、装药密度及间隙[5-6]、含能材料配方[7]、熔铸炸药点火机理[8]以及缓释结构特性[9]等对弹药响应温度、响应烈度的影响研究,已达到既深又广的程度;仿真研究与试验研究既相辅相成又互相补存和促进,能获得点火时刻的温度及其梯度、点火点位置、点火前压力[10]、内部机理的分析[11-12]及点火后的瞬时响应特性[13]等内容。其中关于点火后的含能材料自持反应特性的仿真研究软件,目前只有美国ALE3D软件和Uintah软件。

从上述情况可见,研究弹药的热刺激,无论从试验还是仿真都取得了很大的成就。但是关于纯理论研究点火点位置和点火温度的文章,目前鲜有报道,而理论研究是弹药热刺激研究不可或缺的内容,是对热爆炸理论的完善和补存,具有重要的意义。本文拟采用叠加原理和分离变量方法,首次将炸药非反应性热传导与自热反应热传导拆分,以一维炸药模型为基础,研究慢速烤燃的温度分布及点火点位置的解析解,分析点火点位置的一维变化规律,以期为烤燃研究奠定理论基础。

1 一维数学理论模型

1.1 理论推演的假设

为简化理论计算,需对炸药的烤燃过程作如下假设:

1)炸药为凝聚炸药,炸药在加热过程中不发生相变;

2)弹体外壁均匀升温,升温速率为固定值;

3)忽略壳体与炸药间的接触热阻;

4)炸药的热导率、比热容、密度均为恒值;

5)炸药活化能、指前因子、反应热均为常数;

6)炸药按照零阶动力学定律分解。

1.2 慢速烤燃一维模型

炸药的热传导方程用式(1)[14]描述:

(1)

(2)

当则炸药厚度L=2δ,其中δ为厚度值的一半。则一维无限平板模型的热传导可用式(3)来描述:

(3)

式中:α为热扩散系数,且α=λ/ρc;S(x,t)为热传导方程的源项,用式(4)表示:

(4)

式(3)的定解条件如下:

1)初始条件:T(x,0)=Tr,其中Tr为初始温度;

2)边界条件:T(±δ,t)=κt+Tr,其中κ为升温速率。

2 求解

2.1 温度场的拆分

当没有化学反应时,炸药热传导问题的解析解即非反应性热传导比较容易求解。但是,具有化学反应的热传导方程即反应性热传导是极难获得解析解的。为进一步求解热传导方程式(3),需要用到叠加原理[15],将原问题T(x,t)分解为非反应性热传导项Tt(x,t)和自热反应热传导项Ts(x,t)两个子问题。其中非反应热传导式为

(5)

式(5)相应的定解条件如下:

1)初始条件:Tt(x,0)=Tr;

2)边界条件:Tt(±δ,t)=κt+Tr。

自热反应热传导的方程如下:

(6)

式(6)的定解条件如下:

1)初始条件:Ts(x,0)=0;

2)边界条件:Ts(±δ,t)=0。

则原方程(式(3))的解T(x,t)可通过T(x,t)=Tt(x,t)+Ts(x,t)求得。

2.2 非反应性热传导问题的求解

式(5)的热传导子问题不包含自热源项,即属于没有化学反应的惰性情况下的热传导问题。由于变量x、t相互独立,使用分离变量法[16]将Tt(x,t)写为

Tt(x,t)=X(x)U(t)

(7)

式中:X(x)为位置x的函数;U(t)为时间t的函数。

将式(7)代入式(5),有如下等式:

(8)

(9)

式中:k为常数。

式(8)根据边界条件Tt(±δ,t)=κt+Tr,通过Strum-Liouville理论求解有

Xn(x)=Cnsin[nπ(-x+δ)/(2δ)]

(10)

式中:Cn为常数,X0(x)=C0;固有值λn=nπ,n=0,1,2,3,…。

对式(9)求解,有

Un(t)=Bne(-απ2n2t)/4δ2

(11)

式中:Bn为常数。

则非反应性热传导方程式(5)的通解为

(12)

式中:An为常数,且对于Tt(x,t)解函数首项Tt0(x,t)有Tt0(x,t)=A0。

代入初始条件Tt(x,0)=Tr,进一步求得非反应性热传导方程的精确解Tt(x,t)为

(13)

随着时间t的不断增加,无穷级数项将逐渐减小,非反应性热传导所产生的温度分布将逐渐稳定。其中初始温度Tr作为常数项,不影响非反应性热传导所产生的温度分布。

2.3 自热反应热传导问题的求解

对于式(6)的自热反应热传导问题,非齐次项(即源项)为Arrhenius方程,直接求解是相当复杂的。通过进一步将源项S(x,t)泰勒展开:

(14)

当自热反应产生的温度Ts小于非反应性热传导温度Tt的1%时,源项S(x,t)可取泰勒展开式首项近似代替,作近似后的自热反应热传导方程如下:

(15)

式中:

(16)

对于式(15)的求解,采用分离变量法[17]。将Ts(x,t)、S(x,t)分别按固有函数展开为Dn(t)、Sn(t),于是有

(17)

式中:

(18)

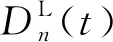
(19)

再将其反变换后,则有

(20)

这样,可解得自热反应热传导方程的解Ts(x,t)为

Ts(x,t)=

(21)

观察解的结构,不难发现式(21)中Ts(x,t)包含Arrhenius温度积分,直接求出其精确的结果极其困难[18]。但Ts(x,t)中常数显然不影响对其最高温度所在位置的求解,即指数前因子A、反应热Q不影响自热反应热传导温度最高值所在位置,进而不影响炸药在烤燃中的点火点位置。随着升温速率κ的增加,炸药两侧升温加快,则点火点位置向边界移动。

3 慢速烤燃试验

3.1 试验设计

设计尺寸为φ75 mm×295 mm烤燃弹,壳体材料选用45号钢,两端带螺纹的端盖连接,端盖和壳体壁厚均为5 mm。内部装药为甘肃银光化学工业集团有限公司生产的RDX炸药,单节药柱直径为57.4 mm,长度为47.5 mm,共6节,药柱总长285 mm,长径比为5,装药密度为1 610 kg/m-3。

为获得烤燃试验过程中,炸药内部的温度的变化情况,在每节药柱中间刻槽埋入φ1 mm的上海自动化仪表股份有限公司生产的WRNK191型铠装电偶(精度为0.1 K,热响应时间≦3 s)。药柱与药柱之间以及药柱与热电偶之间均采用虫胶漆粘接固定。热电偶的温度测点由上至下编号1～5号,两相邻测点及边缘测点至端面的间距均为47.5 mm,温度测点位置如图1所示。由于采用等长压制药柱试验,无法获得其他位置的温度情况。

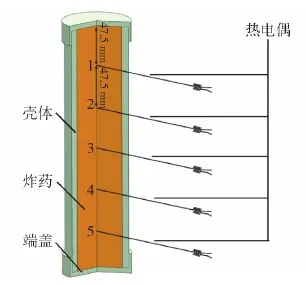
图1 温度测点的位置示意图Fig.1 Location of temperature measuring points

试验弹试验前状态如图2所示。试验采用圆柱形保温箱进行加热,试验装置如图3所示。

图2 试验弹体Fig.2 Tested ammunition

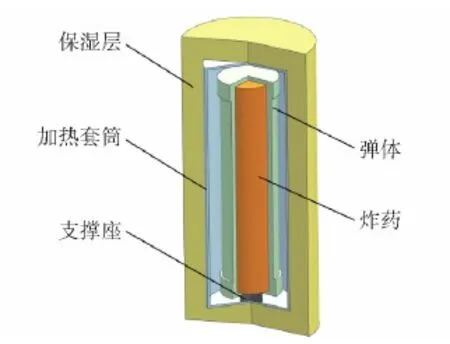
图3 慢速烤燃试验装置Fig.3 Slow-cook test setup

使用日本岛电公司生产的MR13温控仪对烤燃弹外壁进行升温控制,并使用美国Fluke公司的1586A多路测温仪采集各测点的温度数据,采样周期为1 s。从室温305 K开始,以3.3 ℃/h的固定速率升温,直至烤燃弹发生响应。

3.2 试验结果

试验药柱中5支热电偶和外壁1支热电偶在点火时刻的测量结果如表1所示,试验中各测点温度变化曲线如图4所示。由于炸药内部的自热反应随温度的升高而逐渐加剧,临近响应时,各测点的温度迅速升高。从5条测温曲线可见,药柱的两侧1号和5号热电偶测得的温度最高,3号点测得的温度最低,可见点火区域位于药柱两侧,点火时外壁温度为468.9 K。

表1 点火时刻热电偶的测量结果

图4 温度变化曲线Fig.4 Temperature history curves

烤燃弹响应后,试验点产生较深的弹坑,加热套筒与烤燃弹壳体完全碎裂。由于试验在野外沟壑中进行,响应后仅回收到少部分碎片,如图5所示。根据响声及以往同种炸药的烤燃试验情况,综合判断烤燃弹的响应等级为爆轰。

图5 试验结果Fig.5 Test results

4 算例及验证

4.1 检验理论与试验的一致性

为检验理论与试验的一致性,以试验药柱为例,利用表2中的物性参数和动力学参数,对式(21)的解析解进行计算。

表2 RDX炸药物性参数和动力学参数

对于任意长圆柱,单从径向或轴向考虑,传热均属于一维问题,仅考虑径向传热时,因温度沿纵轴均匀分布,没有区别。而单考虑轴向传热时,因温度分布不均匀,能体现出位置的差别。同理,仅考虑自热两个方向也均属于一维问题,故对药柱轴向的温度分布进行计算[19]。

已知炸药厚度 、初始温度为305 K、升温速率κ=3.3 ℃/h。使用Maple数学软件[20]和Clenshaw-Curtis正交方法[21]求解,控制无穷级数的舍入误差不大于0.1%。理论解的药柱沿轴线方向的部分温度值如表3所示。

表3 沿轴线方向的温度值

外壁温度为484.6 K时,理论解与测点测量值的温度分布如图6所示。各测点测量得到的温度分布趋势与理论解的温度分布趋势相符,但是由于试验值是三维结果,而理论仅是一维结果,因此两曲线的弯曲程度有所不同(即对于试验药柱,沿轴向的传热属于一维问题[19])。

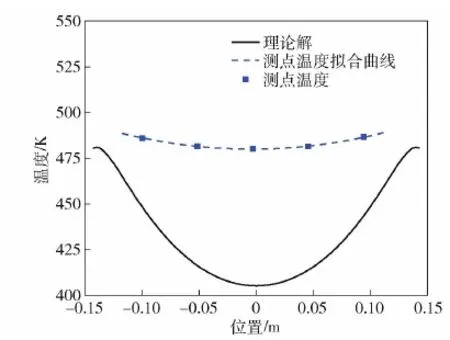
图6 温度分布Fig.6 Temperature distribution

为直观地比较理论解的相对温度分布与试验测得的相对温度分布,将图6中试验测得的温度值、理论解中截取与试验测量范围(-0.095～0.095 m)对应区间的温度值,再根据各自的温度幅值分别作如下归一化处理:

(22)

式中:xN为归一化后的温度值;xi为归一化前的温度值;xmax为归一化前数据中的最高温度值;xmin为归一化前数据中的最低温度值。通过归一化将试验测得的温度值、理论解与试验对应位置的温度值映射到0～1之间,得到各个位置的相对温度分布,如图7所示。理论解各个位置的温度之间的比例与试验结果一致,即理论解的相对温度分布与试验测得的相对温度分布相符,进一步验证了理论解的温度分布的正确性。

图7 相对温度分布Fig.7 Relative temperature distribution

4.2 数值验证

为进一步验证理论解的正确性,使用数值方法对解析解式(21)进行验证。Suceka[22]对热传导方程式(1)进行了有限差分近似。对于无限大平板而言,关于位置x的偏导数可以通过以下差分来近似:

(23)

式中:Δx为将厚度为L的炸药被均匀分为n份后的宽度;上下标用于区分网格对应的时间和位置,上标j为时间序列,下标i为位置序列。

对时间t的偏导数进行同样的有限差分近似:

(24)

式中:Δt为时间增量。

使用有限差分替代热传导方程式(1)中的偏导数,即得到炸药热传导离散方程:

(25)

同理,建立非反应性热传导离散方程如下:

(26)

对于式(25)与式(26)具有相同定解的条件如下:

通过式(25)可以获得任意时刻炸药内部的温度分布;将式(25)与式(26)同时刻的温度结果作差,即可获得该时刻炸药自热反应热传导的温度分布。

以上两种显式方法的稳定性由空间步长和时间步长的比值决定。对于热传导方程,如果满足以下稳定条件[23],则该方法是稳定的:

(27)

稳定性条件保证了有限差分解的稳定性,该条件仅在炸药分解缓慢的情况下,能保证解的精确性。对于慢速烤燃,点火时自热反应产生的热量很低,故适用于该判据。

计算选取RDX炸药为研究对象,计算中使用的物性参数和动力学参数的值如表2所示,炸药厚度、初始温度Tr为305 K、升温速率κ=3.3 ℃/h。代入以上参数,对热传导离散方程式(25)、热传导离散方程式(26)赋予初始条件与边界条件,以时间增量Δt=1 s循环迭代离散方程(即j+1时刻的温度分布由j时刻的温度分布计算得出),并将各个时刻的温度分布进行输出。

点火点的温度变化如图8所示。在D点(加热时间约为177 000 s时)发生点火,自热反应逐渐加剧,温度不再可控,进而发生响应。

图8 点火点温度的理论解与数值解Fig.8 Theoretical and numerical results of the temperature of ignition point

炸药点火温度的理论计算结果与采用文献[22]方法的数值解具有良好的匹配度,理论计算值为468.8 K;数值计算值为468.6 K,误差不超过1%。

点火时刻(外壁温度为480.7 K时),炸药总体温度(即非反应性热传导温度与自热反应热传导温度之和)分布与仅自热反应所产生的温度分布如 图9 所示,点火点位置位于炸药两侧,与试验结果相符。总体温度分布主要受升温边界的影响,由于点火前达到分解能垒的分子数很少,自热反应所产生的温度较低。自热反应所产生的温度的理论计算结果与数值解相比,最大误差为8.8%(误差主要来自于式(14)对源项的近似处理);自热反应温度最高值所在位置的计算结果与数值解相比,最大误差不超过1%。

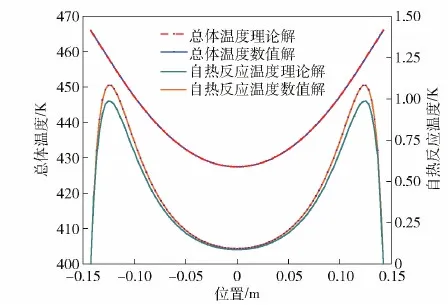
图9 炸药厚度L=0.285 m时的理论计算结果与数值计算结果Fig.9 Theoretical and numerical results with explosive thickness L=0.285 m

5 结果与讨论

自热反应温度最高值的位置是由炸药自热反应与边界的热散失共同作用的结果。图10为不同厚度条件下,炸药自热反应温度最高值随时间的变化情况。由图10可见,随着时间的增加,自热反应温度最高值所在的相对位置(即|x/δ|)将趋于稳定,直至发生点火。

图10 不同厚度炸药自热反应温度最高值所在的相对位置Fig.10 Relative location of the maximum value point of self-heating reaction temperature of explosiveswith different thicknesses

在炸药厚度较薄的情况下,自热反应温度最高位置将迅速移动至中心;随着炸药厚度L的增加,位置移动的相对量逐渐减小,当炸药厚度L>0.3 m时,从50 000 s直至发生点火,自热反应温度最高位置的相对移动量不大于2%。显然可以认为在烤燃试验进行到一定时间之后,温度相对分布趋于稳定,自热反应温度最高值位置随时间不再发生改变,直至点火。这样,可以通过理论计算,预则最高温度及其所在位置,为降低响应等级的结构设计提供便利。

点火时,自热反应温度最高值所在位置至边界的距离变化如图11所示。当炸药厚度L>0.3 m时,随着炸药厚度的进一步增加,自热反应温度最高值所在位置至边界的距离变化不大于2%,且最高值所在位置至边界的距离逐渐趋于稳定。即随着炸药厚度的增加,边界的热散失条件逐渐成为影响点火点位置的重要因素。

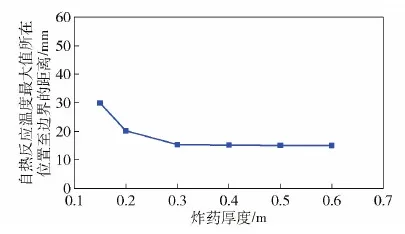
图11 自热反应温度最高值所在位置至边界的距离Fig.11 Distance from the maximum value point of self-heating reaction temperature to boundary

当炸药厚度L>0.3 m时,从边界至中心的自热反应温度梯度如图12所示,随着炸药厚度的增加,点火点附近的自热反应温度梯度趋于恒定。随着炸药厚度的增加,自热反应温度分布的规律相似。

图12 炸药边界到中心的自热反应温度梯度Fig.12 Temperature gradient of self-heating reaction from boundary to center of explosives

6 结论

本文通过理论解析的方法研究一维凝聚炸药慢速烤燃的点火点位置及点火温度。得出以下主要结论:

1)将炸药非反应性热传导与反应性热传导拆分,通过理论方程及计算可得出慢烤条件下一维凝聚炸药内部的温度分布情况及点火点位置,并与试验及数值计算结果进行对比,验证了理论方程及计算的正确性。

2)通过理论计算可得到一维炸药点火时刻仅自热反应所产生的温度分布和自热反应温度最高值所在位置;获得点火时刻一维凝聚炸药温度最高值所在位置及温度梯度沿厚度的变化规律。为烤燃试验点火温度及位置的预测提供了可靠的理论依据。