一类具有线性捕获和其他食物来源的捕食-食饵模型的稳定性研究
张志扬, 李忠
( 福州大学 数学与统计学院, 福州 350108 )
0 引言
由于研究具有捕获的捕食-食饵模型对资源的可持续发展和合理利用具有重要的指导意义,因此近年来许多学者对具有捕获的捕食-食饵模型进行了研究,并取得了良好成果.目前大部分的相关研究是针对唯一食物来源进行的,如:Shang等[1]研究了一类具有常数捕获的Gause型捕食-食饵模型,并分析了模型的稳定性和一些分支现象;Christian[2]提出了一类不连续的具有线性捕获的捕食-食饵模型,并以线性捕获和环境容纳量为参数讨论了模型的分支和稳定性;Mortuja等[3]研究了一类具有非线性捕获和平方根功能性反应的捕食-食饵模型,结果显示当捕获较小时,捕食者群和食饵群将共存并保持平衡;Hu等[4]讨论了一类具有非线性捕获的捕食-食饵系统的稳定性,研究表明该系统会产生Hopf分支和Bogdanov-Takens分支.但在实际中,由于有些捕食者还会具有其他食物来源,因此一些学者研究了具有其他食物来源的捕食-食饵模型的动力学性质.例如:Sen等[5]研究了一种具有Allee效应和其他食物来源的捕食-食饵系统,研究结果显示该模型具有双稳定性和三稳定性;Arancibia等[6]讨论了一类具有其他食物来源的Leslie-Gower捕食-食饵模型,并分析了Allee效应和其他食物来源对系统稳定性和分支的影响;Mondal等[7]研究了一种具有常数捕获和其他食物来源的捕食-食饵模型,并分析了模型的平衡点稳定性和Hopf分支以及时滞对系统动力学性质的影响.基于上述研究,本文研究模型(1)平衡点的局部和全局渐近稳定性,并讨论其他食物来源和捕获对种群稳定性的影响.
(1)
其中:x和y分别表示食饵和捕食者种群的种群密度,r表示食饵种群的内禀增长率,k表示食饵种群的环境容纳量,e表示捕食者种群的捕食率,h0表示捕捞系数,c表示捕食者在种间竞争的能量转化率,n表示捕食者对其他食物来源的能量转化率,d表示捕食者种群的种内竞争强度.
(2)

1 平衡点的局部稳定性及其证明
若系统(2)中的(x(t),y(t))满足初值条件x(0)≥0和y(0)≥0,则有如下定理:
定理1系统(2)的解是恒正和有界的.

令P(x,y)=x(1-x-py)-hx和Q(x,y)=y(m+bx-y),于是由P(x,y)= 0,Q(x,y)= 0可得如下引理:


引理2当h≤1时,E0(0,0)是不稳定的.当h>1时,E0(0,0)是鞍点.
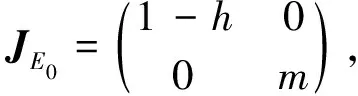
为了讨论E0的稳定性,将系统(2)在平衡点E0处展开可得:
(3)
由于系统(3)中x2项的系数是负的,所以由文献[8]中的定理7.1可知:E0(0,0)是排斥的鞍结点;当h= 1时,平衡点E0是不稳定的.证毕.
引理3①若pm≥1,则E1(0,m)是局部稳定的.②若pm<1,则:当h<1-pm时,E1(0,m)是鞍点;当h= 1-pm时,E1(0,m)是吸引的鞍结点;当h>1-pm时,E1(0,m)是局部稳定的.

下面讨论退化平衡点E1(0,m)的稳定性.对系统(2)作变换,即令x=X,y=Y+m,则系统(2)可变为:
(4)
(5)
由于系统(5)中的负向时间变换和u2项的系数是正的,因此当h= 1-pm时,根据文献[8]中的定理7.1可知E1(0,m)是吸引的鞍结点,即在第一象限内E1(0,m)是稳定的.证毕.
引理4当h<1时,E2(1-h,0)是鞍点.
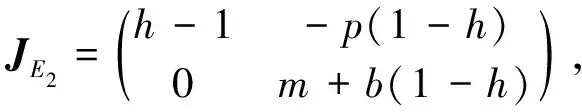
引理5当h<1-pm时,正平衡点E*(x*,y*)是局部稳定的.
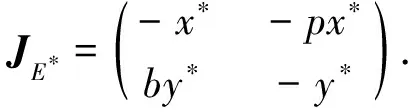
2 平衡点的全局渐近稳定性及其证明
定理2当pm≥1时,边界平衡点E1(0,m)是全局渐近稳定的.
证明由引理1可知:当pm≥1时,系统(2)不存在正平衡点E*,因此系统(2)在第一象限内不存在极限环;当pm≥1且h<1时,系统(2)存在3个边界平衡点E0、E1和E2.于是由引理2—4可知,E0(0,0)是不稳定的,E1(0,m)是局部稳定的,E2(1-h,0)是鞍点.再由定理1进一步可知,系统(2)的解是有界的.由于第一象限内不存在极限环,所以可得边界平衡点E1(0,m)是全局渐近稳定的.
另外,由引理1还可知,当pm≥1且h≥1时,系统(2)存在2个边界平衡点E0和E1.于是由引理2和引理3可知:E0(0,0)是不稳定的,E1(0,m)是局部稳定的.类似上面的分析可知,边界平衡点E1(0,m)是全局渐近稳定的,证毕.
定理3①当pm<1和h<1-pm时,正平衡点E*(x*,y*)是全局渐近稳定的.②当pm<1和h≥1-pm时,边界平衡点E1(0,m)是全局渐近稳定的.
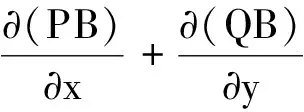
2)由引理1可知,当pm<1和1-pm≤h<1时,系统(2)存在3个边界平衡点E0、E1和E2,其中E0(0,0)是不稳定的,E1(0,m)是局部稳定的,E2(1-h,0)是鞍点.由定理1可知,此时系统(2)的解是有界的,且在第一象限内不存在极限环,所以边界平衡点E1(0,m)是全局渐近稳定的.另外,由引理1还可知,当pm<1和h≥1时,系统(2)存在2个边界平衡点E0和E1,其中E0(0,0)是鞍点,E1(0,m)是局部稳定的.于是类似于pm<1和1-pm≤h<1时的分析可知,E1(0,m)是全局渐近稳定的.
3 数值模拟
例1考虑如下系统的稳定性:
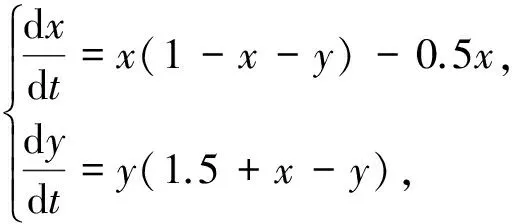
(6)
其中p= 1,b= 1,m= 1.5,h= 0.5.由于h= 0.5<1,因此由引理1可知:系统(6)有3个边界平衡点,分别为E0(0,0)、E1(0,1.5)和E2(0.5,0).
对系统(6)的系数进行计算可得pm= 1.5>1,于是由引理2—4和定理2可知:E0(0,0)是不稳定的,E2(0.5,0)是鞍点,E1(0,1.5)是全局渐近稳定的.图1为系统(6)的相图.由图1可以看出,系统(6)的解均趋向于平衡点E1(0,1.5),即食饵绝灭,捕食者生存.
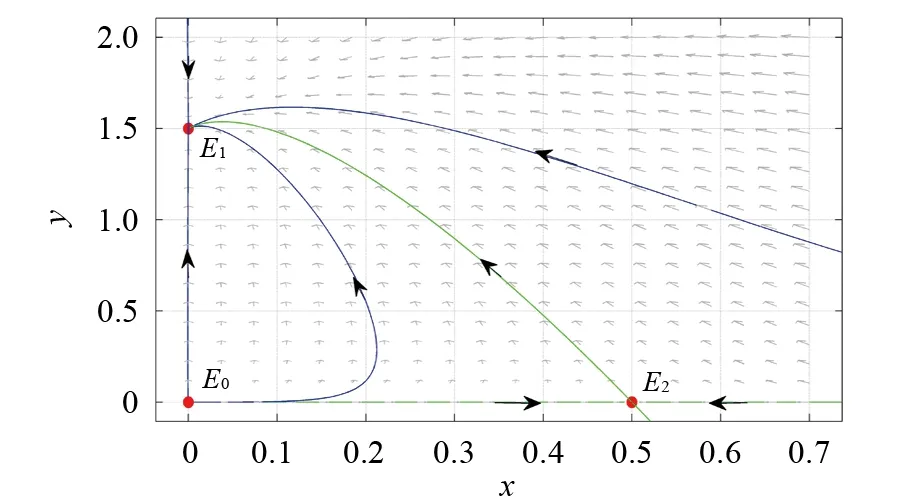
图1 系统(6)的相图
例2考虑如下系统的稳定性:
(7)
其中p= 1,b= 1,m= 0.5,且pm= 0.5<1.
1)在式(7)中取h= 0.3,并对系统(7)的系数进行计算可得h<1-pm= 0.5.于是由引理1可知,系统(7)有3个边界平衡点(E0(0,0)、E1(0,0.5)、E2(0.7,0))和1个正平衡点(E*(0.1,0.6)).再由引理2—5和定理3可知:E0(0,0)是不稳定的,E1(0,0.5)是鞍点,E2(0.7,0)是鞍点,E*(0.1,0.6)是全局渐近稳定的.图2为h= 0.3时系统(7)的相图.由图2可以看出,系统(7)的解均趋向于平衡点E*(0.1,0.6),即食饵和捕食者共存.
2)在式(7)中取h= 0.7,并对系统(7)的系数进行计算可得1-pm= 0.5 图2 h= 0.3时系统(7)的相图 图3 h= 0.7时系统(7)的相图 本文对一类具有线性捕获和其他食物来源的捕食-食饵模型的稳定性进行研究表明:当捕食者的其他食物来源较多时,捕食者的种群数量会增多,从而导致食饵种群绝灭;当捕食者的其他食物来源较少时,食饵种群的捕获率会改变系统的稳定性,即少量的捕获会保持食饵和捕食者种群的共存,而过度捕获则会导致食饵种群的绝灭.本文仅对系统(1)线性捕获的情形进行了研究,在今后研究中我们将对系统(1)的常数捕获及非线性捕获情形进行研究.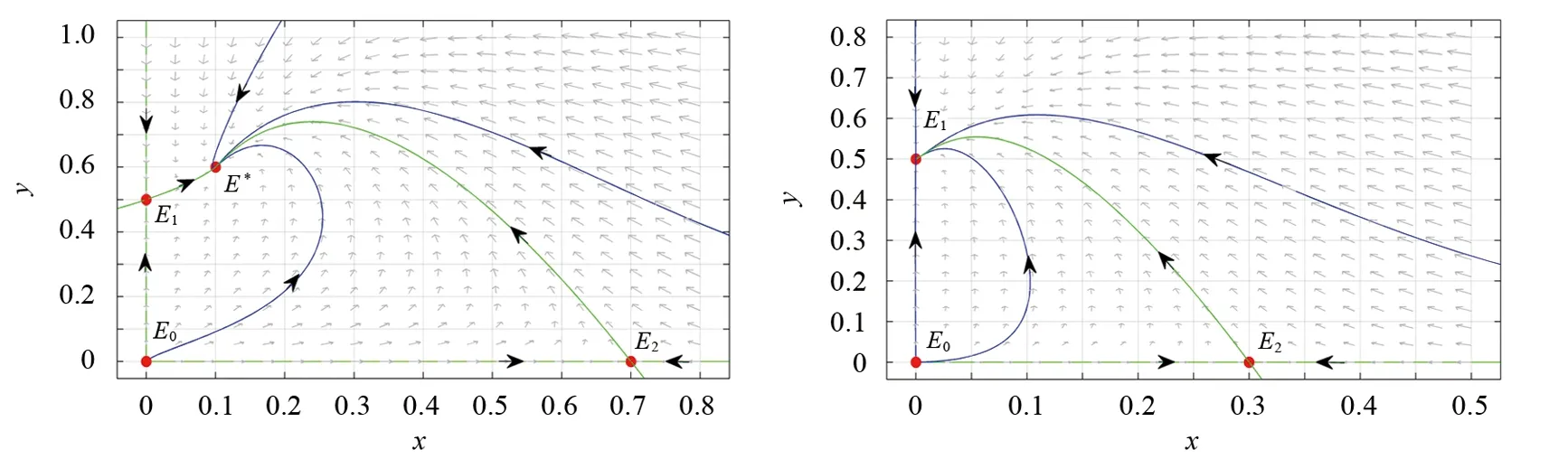
4 结论

