基于XGBoost模型的降雨诱发阶跃型滑坡位移预测

黄智杰,沈 佳,简文彬,樊秀峰,聂 闻

(1. 福州大学 岩土与地质工程系,福建 福州 350108; 2. 福州大学 福建省地质灾害重点实验室,福建 福州 350108;3. 中国科学院海西研究院泉州装备制造研究所,福建 泉州 362200)

0 引言

滑坡是一种常见的自然灾害,目前仅次于地震被列为全球第二大自然灾害,不仅对人们的生命财产安全造成严重的损害,也对自然资源、生态环境等造成严重的破坏[1]。对滑坡的预测一直以来都是广大学者研究的热点之一,其大致可以分为以下几类:1)物理模型预测,即通过揭示滑坡破坏时的物理力学机制并依据相应的知识对滑坡破坏做出预测。例如,HO等[2]在无限边坡稳定性分析以及饱和水位分析的基础上建立了能够预测浅层滑坡发生的物理模型;HONG等[3]通过定义无限边坡模型上安全系数与降雨深度的关系建立了能够从时间与空间上预测降雨型滑坡破坏的模型等。2)统计模型预测,即利用数理统计的相关知识对滑坡进行预测。例如,卢继强等[4]基于指数平滑法及回归分析对滑坡位移进行预测;LI等[5]通过小波分析等理论建立了非线性动态模型进而对滑坡发生的时间进行预测等。3)智能模型预测,即在计算机科学高速发展的背景下,研究人员逐渐将滑坡预测的重点转到通过智能技术、机器学习等手段来实现。例如,张洪吉等[6]通过一维卷积神经网络对四川芦山县区域滑坡进行危险性预测和评价;胡安龙等[7]利用几种优化的SVM(support vector machine)支持向量机模型对湖北竹溪县滑坡稳定性进行预测;温亚楠等[8]利用遥感大数据和机器学习算法对滑坡空间进行预测等。

在上述对滑坡的各类预测中,其中较为直观的就是对滑坡位移进行预测,其预测研究的核心是提升预测的准确性和精确度。在已有的通过机器学习预测滑坡位移的方法中,常用的有:BP(back propagation)神经网络[9-11]、LSTM(long short-term memory)神经网络[12-14]、RNN(recurrent neural network)神经网络[15-16]、RF(random forest)随机森林[17]等。以上方法虽然对滑坡位移的预测取得较好的效果,但对不同类型的滑坡适用性尚存在局限性,且滑坡位移预测的精度仍有提升的空间。例如对于阶跃型滑坡,其位移曲线大致可分为“显著上升段”以及“平稳发展段”,这也给该类滑坡位移预测增添了难度[18]。目前对于阶跃型滑坡位移预测方面的研究,大多数学者主要集中于三峡库区受降雨和库水位等因素联合影响的滑坡,如白家包滑坡、白水河滑坡、八字门滑坡等库区阶跃型滑坡[19-23]。例如,彭令等[19]通过移动平均法将白家包滑坡位移分解为趋势项和周期项,利用多项式拟合及GA-SVR模型分别对两者进行预测;杨背背等[20]同样将白水河滑坡位移分解为趋势项和周期项,采用LSTM模型对周期项位移进行预测;周超等[21]则利用GA-SVM模型对八字门滑坡位移的周期项进行预测。其中,趋势项指滑坡位移中受自身地质情况控制且代表滑坡变形主要趋势的部分;周期项指滑坡位移中受库水位、降雨等外界影响因素控制而呈现出周期性规律的部分。在上述的研究案例中因库水位升降呈现出明显的周期性变化、用于训练的数据时间跨度较长而呈现出更明显的周期性,通常将滑坡位移分解为趋势项和周期项来提升预测精度[24]。但将位移分解为周期项和趋势项的过程中往往存在人为误差[25],用于提取趋势项的数据时间跨度的选择也会影响着模型的预测效果[26]。此外,降雨诱发阶跃型滑坡频发于东南丘陵山地,其主要受降雨的影响而控制,降雨对位移的周期性影响没有上述研究中明显。因此将位移分解为趋势项和周期项的方法对于降雨诱发阶跃型滑坡的预测存在局限性。除此之外,大多数机器学习模型因在对位移不同阶段训练时存在模型过拟合等问题,进而影响后续位移的预测,往往对阶跃型滑坡的预测效果不佳,因此需要一个新的预测模型来解决此类问题。

XGBoost模型是机器学习集成算法中的一类,在已有的滑坡位移预测研究中尚不多见。相较其余算法,因其在目标函数中引入正则项以控制模型复杂程度从而防止模型过拟合等优点,具有更高的精确度和灵活性。因此,文中以福建省泉州市安溪县尧山滑坡为例,在分析该滑坡机制的基础上,利用建立的滑坡远程自动化监测试验场数据,通过Python搭建XGBoost模型,基于最大信息系数理论进行输入特征的筛选后,对该滑坡位移进行预测。结果表明,XGBoost模型对于东南沿海丘陵山地由降雨诱发所致阶跃型滑坡的位移预测具有很高的预测精度,且能实现用较短时间跨度的数据进行训练并达到很好的预测效果。

1 研究区滑坡特征

1.1 滑坡概述

滑坡地灾点位于福建省泉州市安溪县尧山村境内,研究区最高海拔为957 m,最低海拔290 m,高差达650 m,为构造侵蚀中低山地貌。滑坡位于斜坡中前部坡麓处,如图1所示,平面上呈“长条舌状”,后缘横向宽约80 m,前缘宽约200 m,纵向长约350 m。其面积约5.2×104m2,体积约50×104m3,属中型滑坡。滑动面位于表层崩坡积碎石土层与残积黏性土层交界处附近,滑动面深度约为10～13 m,后缘拉张裂缝发育。

根据前期的勘察资料,滑坡地灾点岩土体自上而下可分为:崩坡积碎石土、残积黏性土、全风化凝灰岩、砂土状强风化凝灰岩、碎块状强风化凝灰岩。其中,主要岩土层分布情况及力学参数见表1;主滑面工程地质剖面图对应滑坡工程地质平面图(图1)中的2-2′剖面,如图2所示。

表1 主要岩土层分布及土的物理力学性质Table 1 Distribution of main rock and soil layers and the physical and mechanical properties of soils

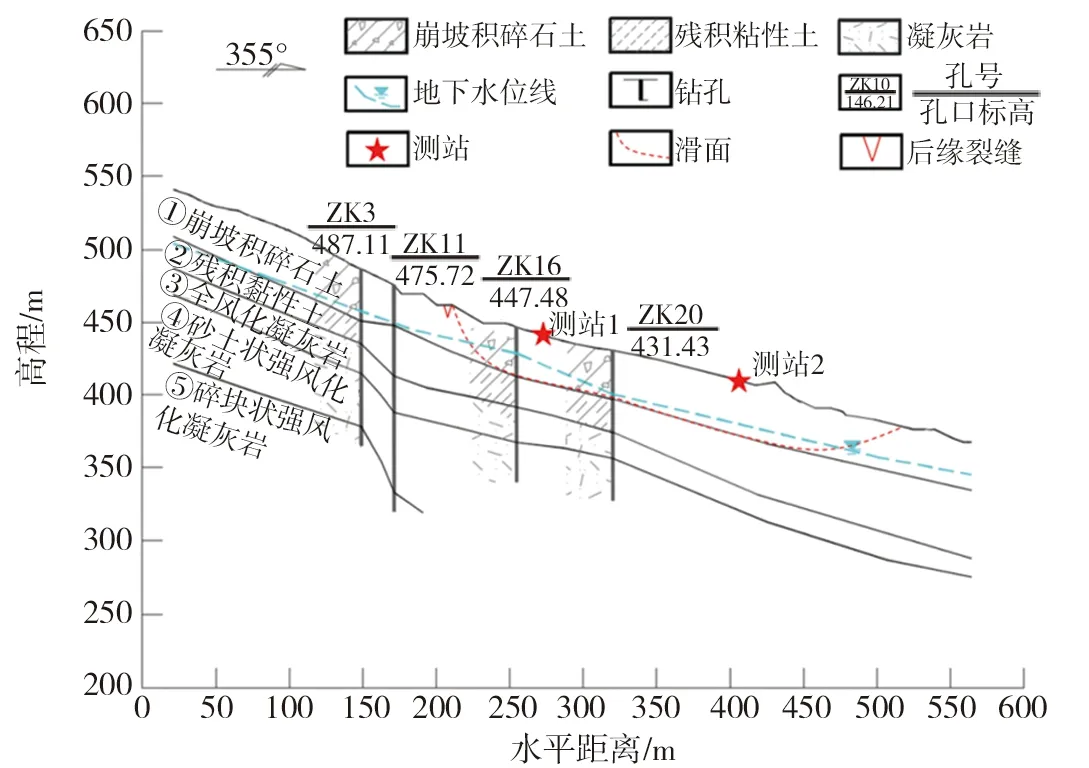
图2 主滑面工程地质剖面图Fig. 2 Engineering geological section of the main sliding surface

滑坡地灾点雨量充沛,年降雨量1 500～2 000 mm,部分特别年份降雨可达2 900 mm。降雨主要集中在3～9月,其中7～9月为常见的台风季节。研究区滑坡呈上陡下缓地形,降雨时大部分雨水顺地势往低处排泄,地灾点区域汇水面积大,约为80万m2。坡体地表水及地下水丰富,其中地下水主要以潜水的形式出现,受大气降水或地表水入渗补给。在降雨的影响下,滑坡位移呈现出“阶跃”特点,即雨季期间滑坡位移总体呈现显著上升趋势;少雨或干旱期间滑坡位移总体呈现出平稳趋势。

1.2 滑坡监测试验场

前期勘察结果表明,滑坡中部主滑面位移较大,两侧位移较小。根据滑坡变形范围与主滑面,选取2个研究点进行自动化监测仪器的布设。滑坡变形范围、主滑面位置及监测布置点A、B(见图3),其中红色实线范围表示滑坡变形范围,红色虚线代表滑坡的主滑面位置。

图3 滑坡范围及监测点示意图Fig. 3 Diagram of the landslide area and the monitoring points

降雨诱发阶跃型滑坡往往需要考虑诸如地下水位、孔隙水压力等因素对滑坡位移的影响。因此,为探究滑坡发生时监测点的地下水位、孔隙水压力及位移指标,本试验场所用的主要监测仪器见表2。其中,渗压计用于测定地下水位的标高,孔隙水压力计用于测定土体的孔隙水压力,固定测斜仪用于测定土体的深部位移。

表2 主要监测仪器一览表Table 2 List of the main monitoring instruments

1.3 滑坡监测数据

试验场从2019年7月25日运行至今,已获得了2年多的降雨量、地下水位、孔隙水压力、深部水平位移等监测数据,以便于对研究区滑坡进行监测与分析。

以监测点A处2019-08-15至2020-09-15期间的日降雨量、地下水位、滑面附近深部孔隙水压力(地下10 m)、深部水平位移(地下12 m)的监测数据为代表(涵盖了研究区旱季与雨季),对滑坡日降雨量、地下水位、深部孔隙水压力这三者与深部水平位移的关系进行探究。

研究区深部水平位移与降雨量的关系总体上呈现出降雨作用下滑坡位移增大(图中实线框区域),无降雨或少雨时滑坡位移较平缓(图中虚线框区域)的趋势,且位移变化呈现出典型的“阶跃”特点,如图4所示。其中,图中阴影部分所示处滑坡位移在无明显降雨时发生阶跃是由于当地开挖盲沟所致。

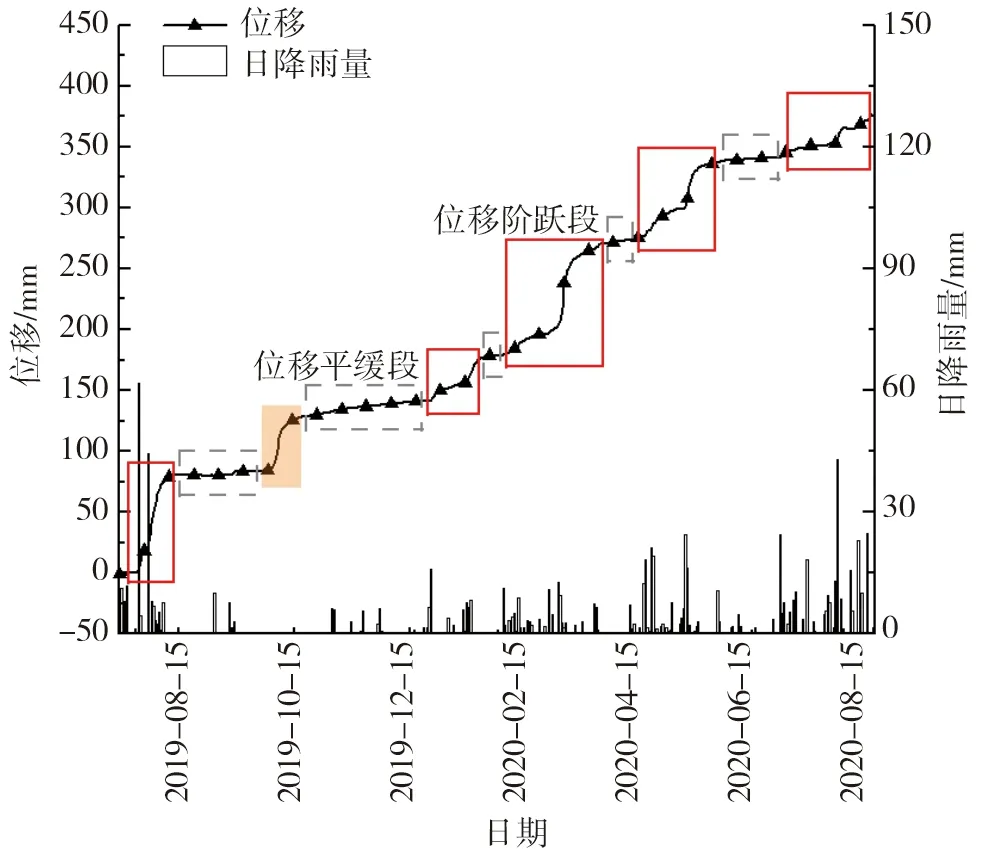
图4 研究区点A降雨量与地下12 m处深部水平位移关系曲线Fig. 4 Relationship curve between rainfall and horizontal displacement at a depth of 12 m below ground at point A in the study area

研究区地下水位和滑面附近深部孔隙水压力的变化趋势相类似,且总体来看,两者均出现地下水位上升或孔隙水压力增大时滑坡位移增大的现象,如图5所示。说明地下水位上升或滑面附近深部孔隙水压力的增大会影响滑坡的位移。相较于地下水位,滑面附近深部孔隙水压力与位移数据之间的内在关系更具规律性:1)如区域1所示,在孔隙水压力由起始位置上升至第1个极大值点期间,滑坡位移曲线的斜率较大,位移速率较快;而后在孔隙水压力由第1个极大值点下降到第1个极小值点期间,位移曲线斜率不断减小,位移速率开始减缓;接着在孔隙水压力回升至第2个极大值点这一阶段,位移速率又有明显增加;在孔隙水压力由第2个极大值点回落至起始位置附近这一阶段,位移速率又出现明显减缓。该现象说明了:孔隙水压力的上升往往伴随着位移速率的增加,上升之后的回落往往伴随着位移速率的降低。2)当孔隙水压力在某个值一定范围内上升并回落时,滑坡往往恰好发生一次阶跃段位移。如区域1、2、3、4所示,在区域1内孔隙水压力从55 kPa附近上升回落、再上升再回落至55 kPa附近时,滑坡发生一次阶跃段位移;在区域2内孔隙水压力由51.2 kPa上升并回落至起始孔压附近,滑坡也发生一次阶跃段位移。区域3与区域4同样体现着类似规律。

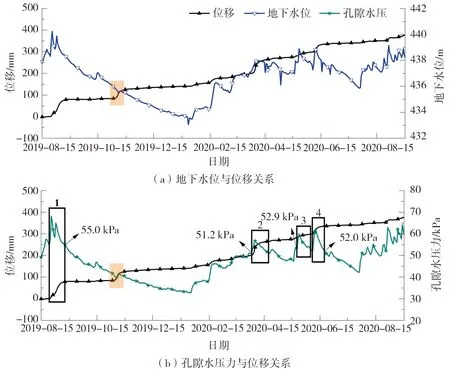
图5 研究区点A地下水位、深部孔隙水压力与深部水平位移关系曲线Fig. 5 Relationship curves between groundwater level, deep pore water pressure and deep horizontal displacement at point A in the study area

孔隙水压力波动的原因主要有以下2点:其一,在降雨的作用下雨水经过滑坡后缘裂缝入渗以及地表入渗,造成滑面附近孔隙水压力发生显著上升;其二,随着雨停以及滑坡体地下水渗流排泄,滑面附近的孔隙水压力会下降。一方面,孔隙水压力会影响着滑坡的位移速率,当孔隙水压力上升时,滑坡的位移速率往往会随之增加;当孔隙水压力回落时,滑坡的稳定性提高,滑坡的位移速率往往会随之减少直至趋于缓慢运动。另一方面,滑坡的速率也会控制着孔隙水压力的变化。当滑坡处于加速阶段时,孔隙水压力由于土体的压缩变形来不及消散,孔隙水压力将会升高;当滑坡处于减速阶段或缓慢运动阶段时,孔隙水压力将得到更有效的消散而降低。

以上分析说明了日降雨量、地下水位、深部孔隙水压力同滑坡位移之间存在着联系,且深部孔隙水压力同滑坡位移之间内在联系的规律性更加明显。

2 滑坡位移预测的XGBoost模型

针对研究区滑坡位移“阶跃”变化的特点,基于前述监测数据建立集成算法XGBoost模型,对该降雨诱发阶跃型滑坡位移进行预测。

2.1 最大信息系数(MIC)

最大信息系数(maximum information coefficient, MIC)由哈佛大学RESHEF等[27]于2014年提出,是用于衡量2个变量x和y之间关联程度的测度。MIC测度具有2个重要的属性:普适性和均匀性。普适性指的是MIC可表征多种函数关系,包括线性与非线性关系及其它多种函数关系;均匀性是指给定的函数关系受到相同水平的噪声干扰时,它们的MIC值与干扰前是相近的,从而最大程度上减轻了同等水平的噪声对用MIC值比较变量相关性时的干扰。

MIC的计算原理如下:

设变量x与变量y构成的集合为D,其中X={xi,i=1,2,…,n},Y={yi,i=1,2,…,n},n为样本数量。在x轴、y轴上依次划分a个格子、b个格子,即可得到一个a×b的网格G,并且改变不同的a、b值可得到不同的网格。定义网格G下D的最大互信息公式为:

MI*(D,x,y)=maxI(D|G)

(1)

将所有不同划分得到的MI值组成特征矩阵并进行规范化,得D的特征矩阵为:

(2)

然后对特征矩阵取最大值,即得到MIC:

MIC(D)=maxxy≤B(n){M(D)x,y}

(3)

式中:B(n)为网格数量的上限,其值约为n的0.6次幂。

基于其属性及优势,文中用最大信息系数来寻找与位移数据高度相关的监测指标作为XGBoost模型的输入特征。

2.2 XGBoost算法

XGBoost算法[28]是集成学习算法中Boosting类的一个代表,其方法是将许多基础模型(包括分类与回归决策树、线性模型)集成在一起,形成一个能力较强的模型,从而达到预测分类问题或回归问题的效果。其原理为:模型会产生多轮迭代,且每轮迭代中会产生一个弱分类器。通过在上一轮分类器的残差基础上训练,下一轮分类器的精度将得到提高。最后,对所有弱分类器的预测结果加权求和得到最终结果。

XGBoost算法对第i个样本的预测过程如式(4)所示:

(4)

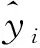
XGBoost算法中对于回归问题构造平方项损失作为目标函数,用泰勒级数对目标函数进行二项展开以解决目标函数优化困难的问题,并且用梯度下降算法进行优化求解。XGBoost算法的目标函数一般形式如式(5):

(5)

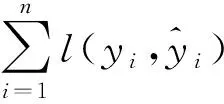
(6)

式中:γ、λ为模型复杂度变量;T为叶子节点个数;ωj为叶节点j的权重。对式(5)目标函数泰勒展开后求偏导并令其等于0,即可得到叶子节点j对应的最优解:

(7)

此时目标函数为:

(8)

式中:Gj=∑gi,Hj=∑hi,gi和hi分别为目标函数的一阶导数、二阶导数。其值越小,代表模型的结构越好,计算的精度越高。

XGBoost模型相较于其它机器学习模型在预测阶跃型滑坡位移上具有如下的优点:1)预测精度更高。阶跃型滑坡在位移上呈现出“显著上升”与“平稳发展”阶段交替变化的特点,且大多数机器学习模型因在对位移不同阶段训练时容易产生过拟合,会影响下一阶段的预测精度。XGBoost模型通过在目标函数中引入正则项来减少对数据的过拟合,从而改善这一问题,提升了预测的精度;2)运行速度更快。模型支持并行化,可以利用多线程对每个事先存储好的样本预排序块并行计算以寻找每个特征的最佳分割点,从而达到运行速度快的特点;3)算法效率更高。模型考虑了训练数据为稀疏值的情形,可为缺失值指定分支的默认方向,极大地提升算法的效率。

3 滑坡监测数据处理

3.1 输入特征筛选

在滑坡监测系统中,监测点降雨量、地下水位、孔隙水压力数据按照固定的频率实时传输到系统中。由于各因素对滑坡位移的影响程度及关联性不同,因此需要进行特征筛选来确定与滑坡位移相关性最大的因素,以此作为滑坡位移预测的输入特征。降雨量、地下水位、孔隙水压力同位移数据之间存在复杂的非线性关系,且在自然状态下监测点所测数据总会受到一定的环境干扰。因MIC具有普适性和均匀性,故选用MIC来分别衡量降雨量、地下水位、孔隙水压力与位移数据之间的相关性。

文中选取了2019-08-15～2020-09-15期间监测点A的日降雨量、地下水位、深部孔隙水压力、深部水平位移数据,运用Python分别计算了日降雨量、地下水位、深部孔隙水压力这三者同深部水平位移数据的MIC值,计算结果见图6。在此时间序列中,地下水位、深部孔隙水压力同位移之间的MIC值较大,有很好的关联程度。因深部孔隙水压力同位移之间的MIC值最大,结合1.3节中深部孔隙水压力与位移之间的内在联系,选取孔隙水压力作为XGBoost模型中的输入特征对位移进行预测。

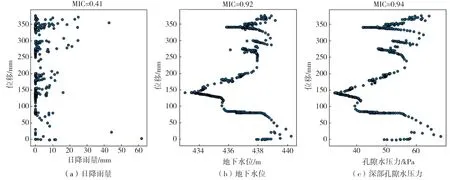
图6 各影响因素同深部水平位移数据的散点图及对应的MIC值Fig. 6 Scatterplots of influencing factors and deep horizontal displacement and the corresponding MIC values

3.2 XGBoost模型中数据处理

依据输入特征筛选的结果,将安溪县尧山滑坡2019-08-15至2020-09-15期间内单日孔隙水压力、深部水平位移作为数据集。首先将原始数据转化为监督学习形式,使得原有的时间序列转化为输入时间序列以及输出时间序列,从而利用输入时间序列对输出时间序列进行预测。其次将数据集划分成训练集和测试集。具体而言,其划分采用前向验证的方式,即:1)为了使模型有充足的数据进行训练且保证预测序列的长度和精度,参照大多数机器学习数据集的划分[29-31],首先对数据集按照7∶3的比例初步划分为第一次的训练集、测试集;2)在模型对训练集进行拟合、训练,得出测试集中一定数量的预测值后,会将这些预测值纳入到原有训练集中使之成为新的训练集,再对新的测试集进行一定数量的预测,以此类推。其优点是充分利用测试集中的数据,将其加入拟合,以便于在下一次预测中达到更好的预测效果。文中将2019-08-15至2020-05-15期间的数据作为第1次的训练集,2020-05-16至2020-09-15期间内的数据作为第1次的测试集,依据上述过程,对滑坡位移进行预测和校验。

经过预测结果的比对,为取得最好的预测效果,最终模型将t-1、t-2 天的孔隙水压力数据、位移数据作为输入变量来预测第t天的位移量。前向验证中每次预测的数量为1,即:每次对原有训练集进行拟合、训练后,得出一个新的预测值,并将其纳入原有的训练集中成为一个新的训练集,继续进行预测。

4 滑坡位移预测结果及分析

文中利用XGBoost模型,将某一时间点当天及前一天的孔隙水压力和位移数据作为输入特征,从而预测该时间点后一天的位移数据。文中采用平均绝对误差MAE(mean absolute error)以及拟合优度R2来评价模型的预测效果,其中MAE是预测样本绝对误差的平均值,可用来体现预测样本的误差程度;R2可用来检验位移预测曲线和实际位移曲线之间的拟合程度。

降雨诱发阶跃型滑坡滑面附近的深部水平位移呈现出复杂的非线性及明显的“阶跃”性,见图4。XGBoost模型因在数据划分时采用前向验证的划分方式、在模型中引入正则项控制模型过拟合等优点,能在同等条件下相较于大多数机器学习模型实现更高的预测精度。为了比较XGBoost模型相较于大多数机器学习模型在预测阶跃型滑坡位移上的优势,分别选取XGBoost模型、LSTM神经网络模型、SVM支持向量机模型以及PLS(partial least squares)偏最小二乘法模型在同等情况下对滑面附近水平位移进行预测,其对比结果如图7所示。图中,通过XGBoost模型得到的预测值能很好地反映位移的变化趋势且贴近实际值,其MAE=1.059,R2=0.994,说明利用XGBoost模型进行降雨诱发阶跃型滑坡位移预测,能实现很好的预测精度。

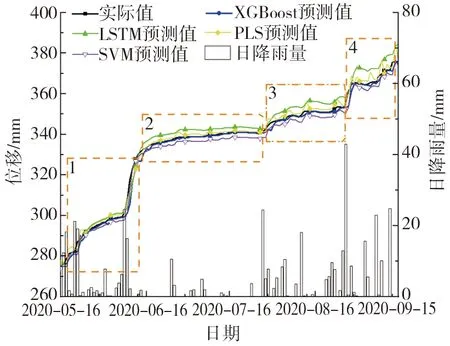
图7 不同机器学习模型位移预测对比图Fig. 7 Comparison of displacement prediction by different machine learning models

进一步分析,在区域1内XGBoost模型、LSTM模型、SVM支持向量机模型、PLS偏最小二乘法模型均能取得较好的预测效果;随着预测天数的增加,LSTM模型、SVM支持向量机模型、PLS偏最小二乘法模型的预测误差将逐渐增大(如图中的区域2、3、4)。误差增大的原因推测是3种模型在对阶跃型滑坡位移不同阶段训练时易造成局部过拟合,进而影响下一阶段的预测效果。例如,3种模型对区域1的预测效果较好,但因存在过拟合的问题,区域2的预测出现明显误差。同理,区域3和区域4也出现明显误差,且这种误差呈持续放大的趋势。除此之外,SVM支持向量机模型、PLS偏最小二乘法模型对位移的预测在区域3和区域4中存在明显的波动和不稳定性,与实际位移存在较大的偏差。

因此,XGBoost模型对降雨诱发阶跃型滑坡位移的预测能充分反映滑坡自身特性和外部因素的影响。其在数据集划分和控制模型过拟合等方面具有显著优势,能用时间跨度较少的数据较高精度地预测出数月内的滑坡变形,且其预测能力要明显强于LSTM神经网络模型、SVM支持向量机模型以及PLS偏最小二乘法模型。文中所述不同机器学习模型的对比情况见表3。

表3 不同机器学习模型的对比Table 3 Comparisons of different machine learning models

5 结论

文中以福建省泉州市安溪县尧山滑坡为例,基于最大信息系数理论选定输入特征,搭建XGBoost模型对降雨诱发阶跃型滑坡位移进行预测。模型通过采用前向验证方式划分数据集、将数据转换成监督学习形式、在目标函数中引入正则项控制模型过拟合等,实现了对滑坡位移的高精度预测。最后,将其预测结果与LSTM神经网络模型、SVM支持向量机模型以及PLS偏最小二乘法模型的预测结果对比。主要结论如下:

1)最大信息系数用于衡量2个变量x和y之间的关联程度,因其具有普适性和均匀性的特点,适用于判断自然状态下滑坡各指标之间的关联程度,可用于预测模型中输入特征的选择。通过比较日降雨量、地下水位、深部孔隙水压力这三者数据与滑面附近深部水平位移数据的MIC值,选定深部孔隙水压力作为位移预测模型的输入特征之一。

2)XGBoost模型因其在目标函数中引入正则项控制模型的过拟合、采用前向验证方式划分数据集等优点,相较于大多数机器学习模型能更加精确地预测出滑坡的位移。文中用LSTM神经网络模型、SVM支持向量机模型以及PLS偏最小二乘法模型的预测效果与XGBoost模型进行对比,结果表明XGBoost模型预测效果较其余模型有很大提升,预测精度更高、预测效果更加稳定。

3)文中建立的模型通过对监测数据的分析,充分考虑了降雨诱发阶跃型滑坡的机制,具有明确的物理意义。其能较好地对东南丘陵山地降雨诱发阶跃型滑坡的位移进行预测,并对此类滑坡早期监测预警具有重要的参考意义。