基于可靠性的索穹顶结构优化设计
陈联盟,李泽斌,章 禾,刘毅杰,周一一,董石麟
(1. 温州大学 建筑工程学院,浙江 温州 325035; 2. 常州工学院 土木与建筑学院,江苏 常州 213002;3. 浙江大学 空间结构研究中心,浙江 杭州 310027)
0 引言
索穹顶结构是一类基于Fuller整体张拉思想、由拉索和压杆为基本单元、通过张拉成形的自平衡柔性空间结构。由于能充分利用拉索的高强性,且能通过施加和优化预应力分布来提供和优化结构刚度,故该类结构具有跨度大、构造轻盈、形态优美、经济性能卓越等诸多优点,在实际工程中得到广泛应用,目前主要包括Geiger型和Levy型两类索穹顶结构类型。然而实际工程中,Geiger型索穹顶结构由于索桁架平面外刚度较弱,且结构冗余度低,在不对称荷载作用下容易失稳[1];Levy型索穹顶结构对施工误差敏感,使得结构实际状态与理想状态存在一定偏差,进而影响结构承载性能[2-3]。另外随着社会的不断发展,以索穹顶结构为代表的索杆张力结构在各种极端环境条件下各种倒塌情况时有发生。1978年美国Hartford公民中心体育馆的屋盖结构以及2010年美国明尼苏达Minnesota Vikings 索膜结构体育馆均因暴风雪极端天气发生整体倒塌事故。因此,为保证该类结构在各种荷载条件下具有足够的安全性、耐久性和适用性,需通过合理设计保证其具有足够的可靠性。
可靠度是反映结构可靠性的指标,其思想可以追溯至19世纪初,当时常使用基于实际经验的安全系数来确保结构的正常工作[4],其本质上是对实际工程中各种不确定因素的综合估计。到了20世纪初,工程界基本确立了使用概率论反映客观存在的随机变量,并以此度量结构可靠度的研究路线。MAYER[5]首次系统阐述了使用概率论分析结构可靠度的思路。随后FREADENTBAL[6]、LIND[7]等学者进一步发展了结构可靠性理论并进入实用阶段。赵国藩[8]较早地采用数理统计的方法研究了荷载、材料强度的概率分布及基于可靠度理论的结构极限状态设计方法。因此,基于可靠度的结构性能分析理论以及在此基础上构建的工程设计方法是目前非常基本又非常重要的分析方法[9-10]。
当前索穹顶结构的优化设计一般集中在4个层面,即预应力优化[11-12]、截面优化[13]、形状优化[13-14]及拓扑优化[14-15],其中截面优化、形状优化及拓扑优化设计多围绕着结构质量最轻这一优化目标展开。实际上,索穹顶结构的自重本身就较轻,用钢量一般不到30 kg/m2,对其进一步进行质量优化意义不大;另一方面,随着社会的不断发展,面对更为复杂的结构形式、更为极端的气候条件,对于索穹顶结构自身的各项性能必然有着更为严格的要求。因此,开展基于结构性能(如可靠性)的优化设计,对于索穹顶结构的进一步推广应用具有较强的理论研究和工程应用价值。
文中从可靠性角度出发,首先提出基于索穹顶结构非线性特性的结构可靠度量化评价指标,结合Geiger型索穹顶结构模型,分析构件截面积对结构可靠度的影响规律;然后使用遗传算法,在不增加结构质量的前提下开展基于结构可靠性的截面优化设计;在此基础上,基于提高结构冗余度的优化理念,进一步提出一种布索优化方案以提高结构整体可靠性;最后再次使用遗传算法,对布索优化方案下的索穹顶结构进行截面优化设计,寻求最优的结构形式和材料分布,因此文中的研究具有较高的理论研究和工程应用价值。
1 索穹顶结构可靠性分析方法
1.1 索杆体系可靠度计算方法
工程中常采用可靠性框图法来描述系统可靠性。分析时,首先根据Maxwell准则,判断结构是串联系统、并联系统还是同时具有串联和并联系统。如果拆除任意杆件均会引起结构变成可变体系,则该体系为串联系统,此时结构整体可靠度为:
(1)
式中,pi为第i根杆件的可靠度。如果只要有一个单元正常工作,整个系统便能正常工作,则该系统为并联系统,此时结构整体可靠度为:
(2)
式中,Xf,i为第i个单元的失效概率。如果结构中既有串联系统又有并联系统,即表决系统,则在由n个单元组成的系统中,只有当至少k个单元正常工作时,整个系统才能正常工作,此时结构可靠度为:
(3)
式中,Xj为第j个单元正常工作的概率。
1.2 索穹顶结构杆件可靠度计算方法
文中主要基于一次二阶矩理论中的中心点法来计算杆件可靠度,即:
pi=Φ(βi)
(4)
式中:函数Φ(x)为标准正态分布函数;βi为单根杆件的可靠指标,其计算方法为:
(5)
式中:μr,i、μs,i分别为第i根杆件强度与应力的平均值;σr,i、σs,i分别为第i根杆件强度与应力的标准差。μr,i的取值可以参考《钢结构设计规范》中的相关规定,μs,i值可通过读取各杆件的应力值再对其求平均值得到。σr,i采用式(6)求得,
σr,i=cv×μr,i
(6)
式中,cv为变异系数,文中荷载、拉索类杆件强度及压杆类杆件强度的变异系数分别取0.074、0.08和0.047[16]。另外,虽然荷载服从正态分布,但由于索穹顶结构为非线性结构,故σs,i与us,i之间的关系无法直接通过简单的线性关系式得出,需使用以下方法计算σs,i值。
假定结构实际承受荷载F(t)为常规设计荷载值P与荷载干扰值w(t)之和,即:
F(t)=P+w(t)
(7)
式中,干扰值w(t)服从 (0,σp)的正态分布,则F(t)服从(P,σp)的正态分布。根据概率论中的“3σ”法则:尽管真实荷载的取值区间为(-∞,+∞),但在区间(P-3σp,P+3σp)发生干扰的概率达99.74%。因此,在施加干扰值时,可以近似的将干扰值限定在(-3σp,+3σp)之内。进一步将荷载干扰值的区间分为m段(为方便计算,m一般取偶数,文中取100),由于其关于y轴对称,故以下只讨论区间(-3σp,0)上的情况。
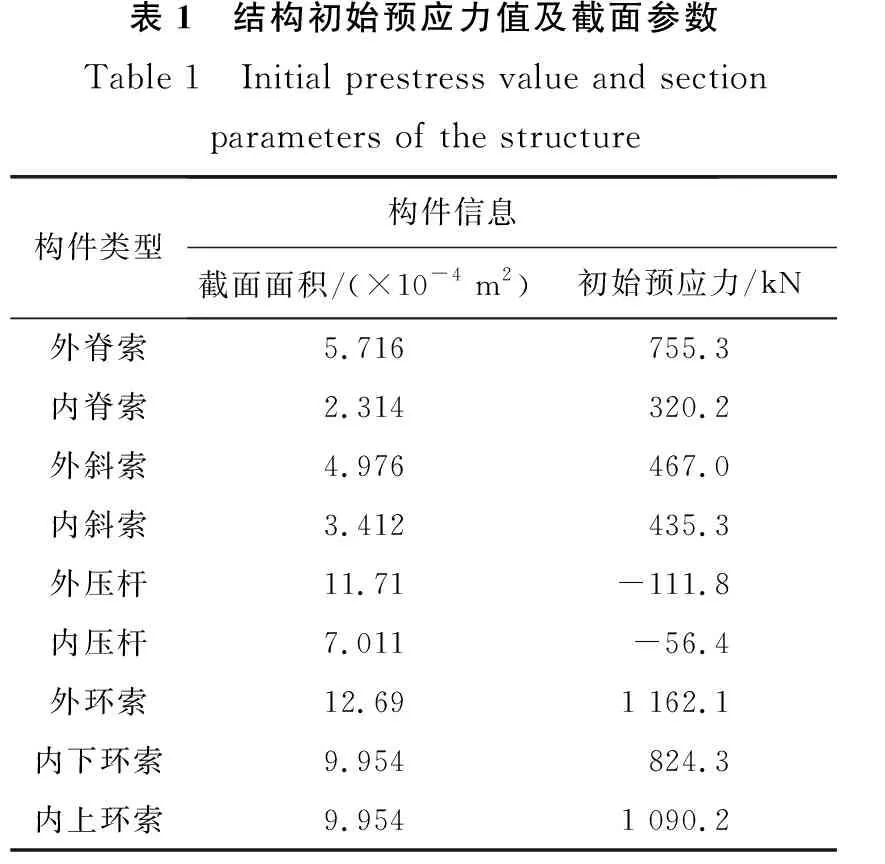
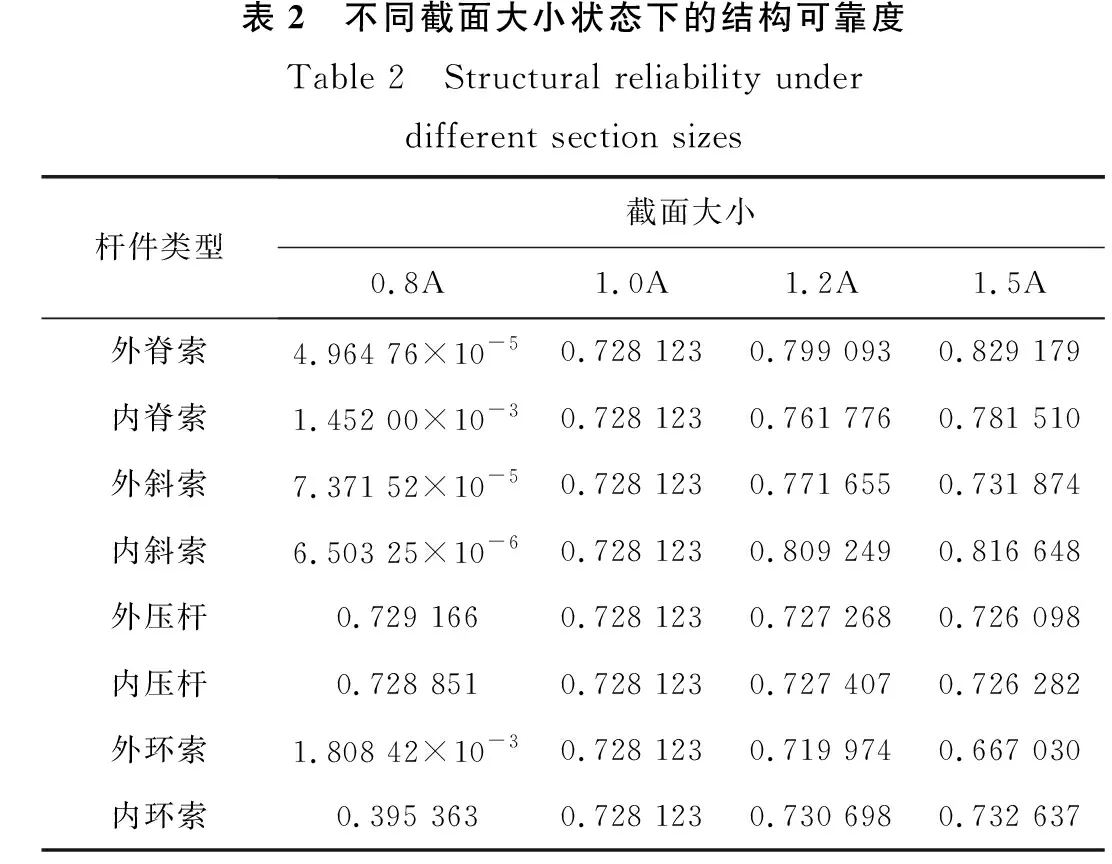
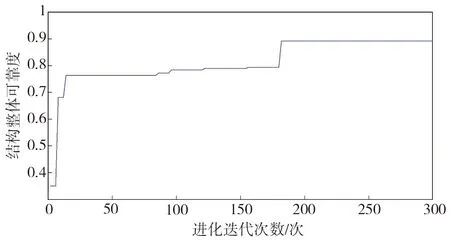
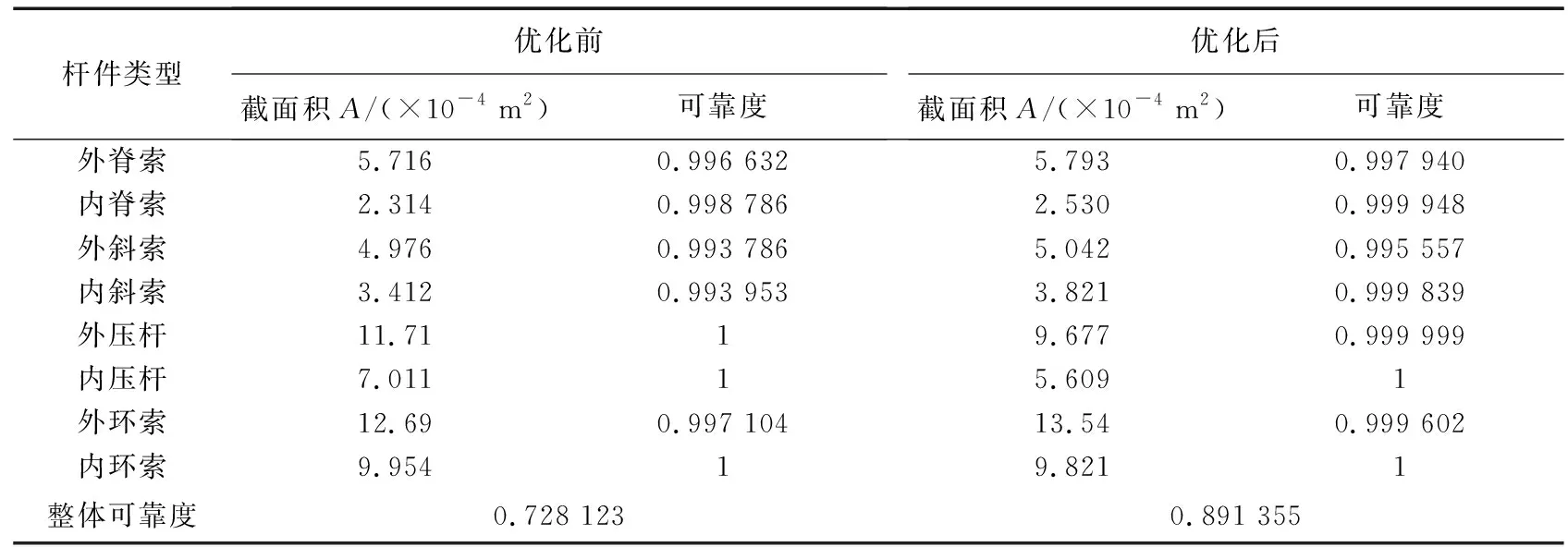
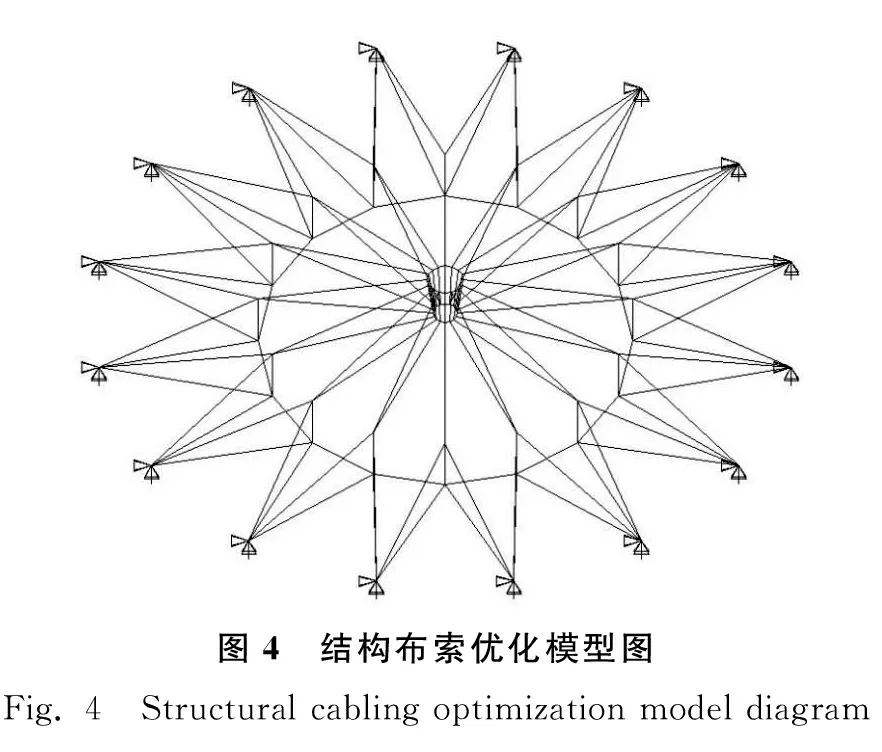
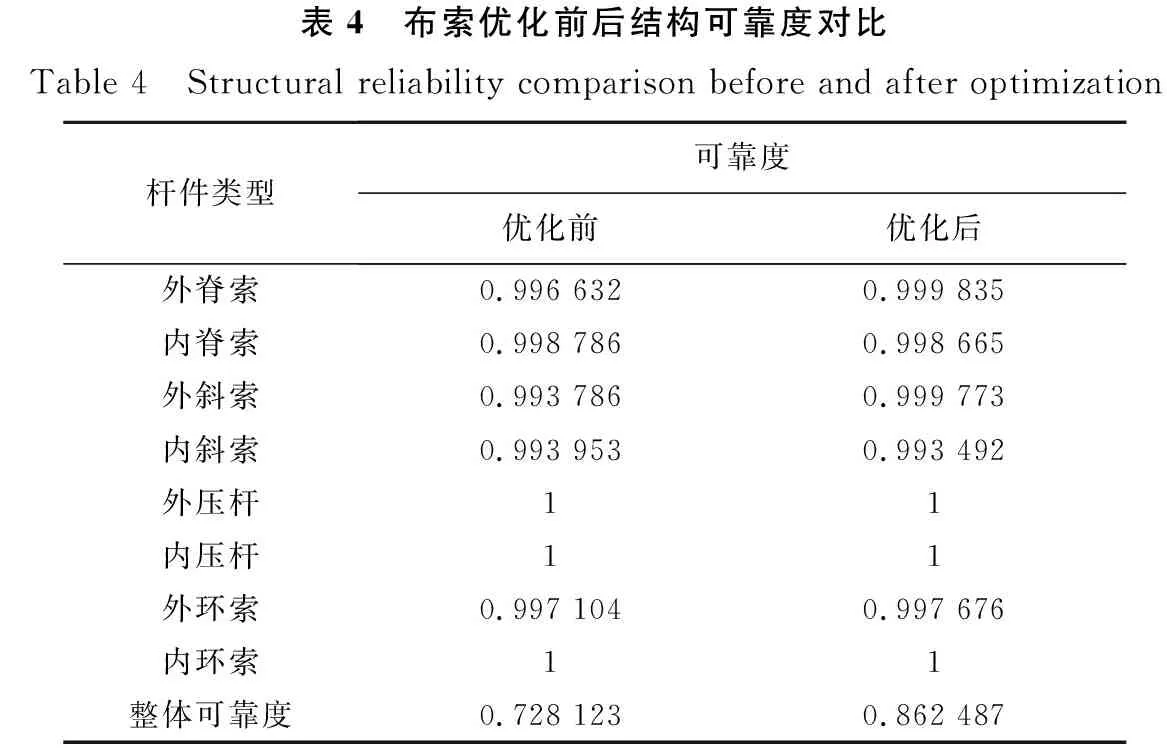
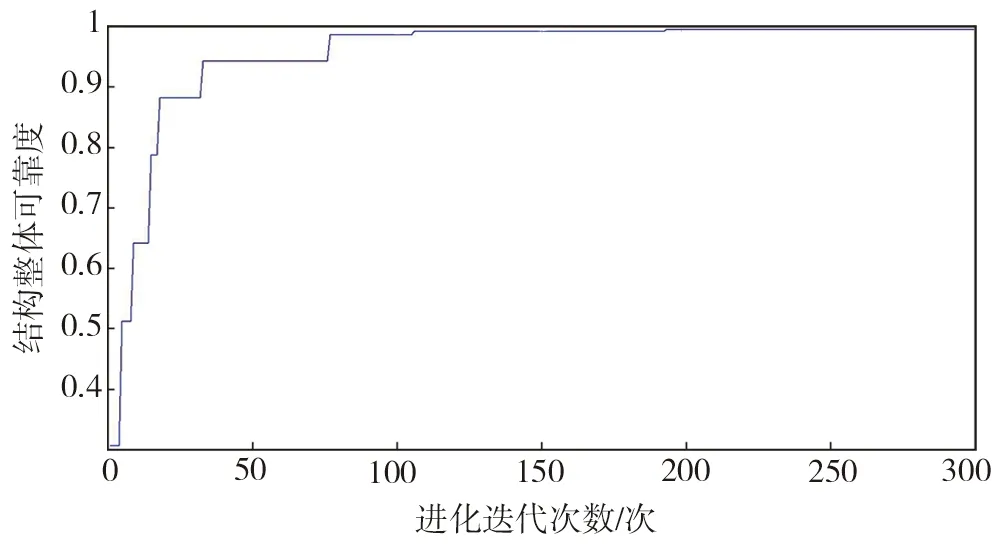
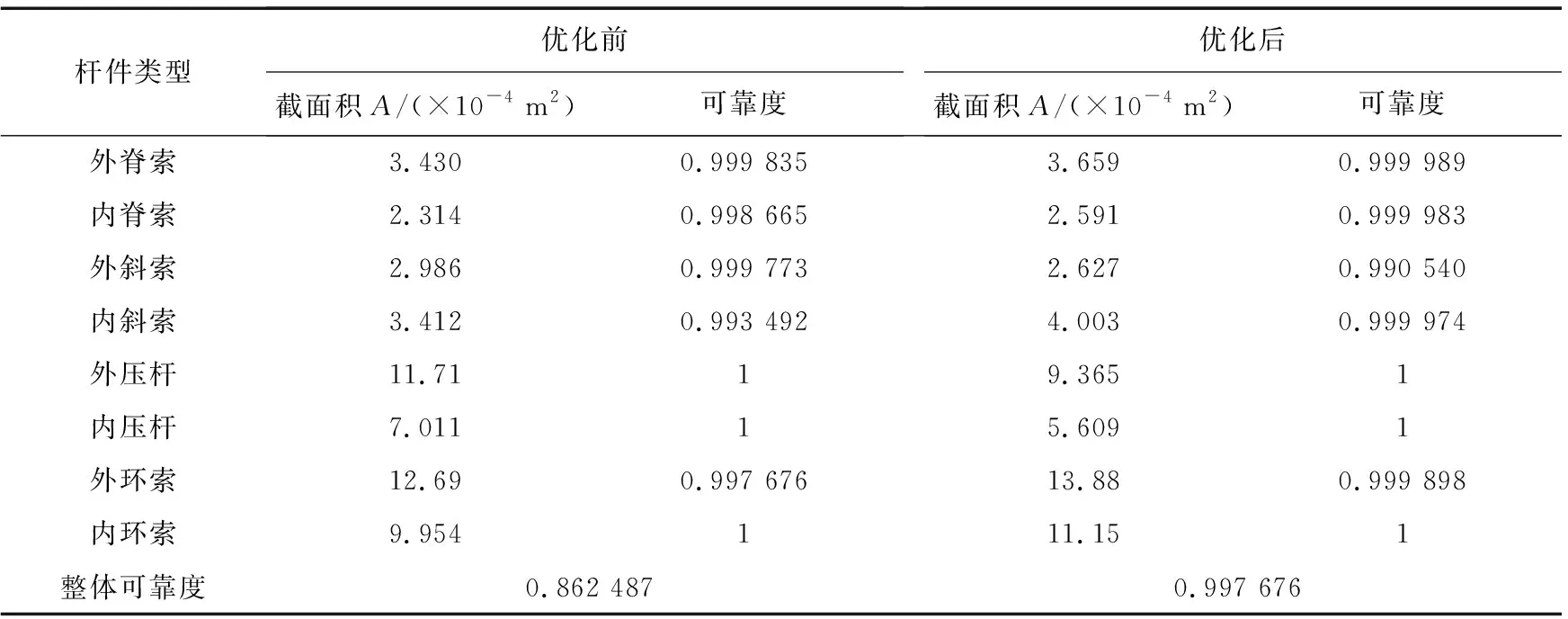
取每个区间上的中点值近似表示该区间上的荷载干扰值大小,则第k个区间为(3σp·(k-1)/(m/2),3σp·k/(m/2),该区间上的荷载干扰值大小为3σp·(2k-1)/m, 0 (8) 对该区间上的概率密度函数积分作为第k个区间的权重系数Q(k), (9) 则σs应力标准差的计算公式为: (10) 式中:uk,i为干扰值发生在第k个区间上时,第i根杆件的应力大小;当干扰值发生在区间(0,+3σp)上时,σs,i的计算原理与上述完全相同,这里不再赘述。 结合Geiger型索穹顶结构案例,分析结构可靠度及杆件截面对结构可靠性能的影响规律。结构跨度71.2 m,矢高5.5 m,环向16等分。结构设置一道环索,中心设置拉力环。结构支座为固定铰支座,设计荷载0.4 kN/m2。结构剖面图如图1所示,构件材料参数以及初始预应力[17]如表1所示。拉索和压杆弹模分别为160、206 GPa。 图1 结构剖面尺寸Fig. 1 Structure section and dimensions 模型包含144根杆件,分为外脊索、内脊索、外斜索、内斜索、外压杆、内压杆、外环索、内下环索、内上环索共9个子系统。其中,内下环索与内上环索同属于内环索类杆件,为简化方便起见,文中分析时两者的截面积均保持一致,统称内环索。 分别计算各类型杆件在不同截面积(0.8、1.0、1.2、1.5倍初始截面)时结构整体可靠度,结果如表2所示,可见:1)外脊索、内脊索、外斜索、内斜索、外压杆、内压杆、外环索、内环索8类杆件截面由初始大小增大到1.5倍截面积时,结构整体的可靠度分别提高了13.88%、7.33%、0.52%、12.16%、-0.28%、-0.03%、-8.39%、0.06%,负值表示减小,表明不同杆件的截面变化对结构整体可靠度产生不同的影响。2)增大脊索类与斜索类杆件截面时,结构整体可靠度总体上会增大。3)而增大压杆类与外环索截面积时,会使结构整体可靠度减小,原因是对于压杆来说,其在初始截面时杆件可靠度已达上限1,增大压杆截面将增加结构整体质量,增大其余杆件的工作负担,进而导致结构整体可靠度下降;对于外环索来说,虽然增大截面积可以提高构件可靠度,但是由于外环索的杆件长度较长、截面较大,故增大其截面将会使结构增加较多质量,使得其它杆件的可靠度出现不同程度的减小,从而导致结构整体可靠度减小。 基于前文分析的各类杆件截面面积变化对于结构可靠度具有不同的影响规律,本节进一步对上述Geiger型索穹顶进行基于结构可靠性的截面优化设计。在优化分析中,直接基于ANSYS软件中的零阶和一阶优化算法适用于线性结构,而对于非线性结构其准确性会大大降低,而遗传优化算法采用生物仿生进化原理,具有与问题领域无关的全局搜索能力,且计算准确度高,故文中采用遗传算法对结构进行截面优化分析与设计,基本思路为: 1)使用Matlab编写遗传算法主程序,设置初始参数,确定优化目标并选择优化变量,限定优化变量的取值范围,并采用二进制编码生成初始种群。文中,种群大小设为15,字符串长度设为32,交叉概率为0.8,变异概率为0.2,进化迭代次数设为300次。 2)将生成的种群导入有限元分析软件ANSYS,建模并计算种群内所有个体的适应度值,即结构可靠度。计算得到的适应度值个数应与种群内个体数相等。 3)将ANSYS计算结果导入Matlab,对适应度值按最大值进行排序,提取初始种群中的最佳个体,并对其进行复制、交叉和变异,以此进行循环迭代计算,直至迭代次数达到设定值。 优化的具体过程如图2所示。 图2 遗传算法优化流程示意图Fig. 2 Schematic diagram of genetic algorithm optimization process 文中探索结构总质量不增加前提下,通过优化杆件截面和材料分布,使得结构整体可靠度尽可能大,即探索Psys值最大,优化目标为maxPsys。各类杆件截面大小变化范围为初始截面值的0.8~1.2倍,且荷载作用下应力不能超过屈服点。其数学优化模型可表示为: (11) 截面优化迭代过程如图3所示,优化结果如表3所示,可见,1)优化迭代到170次后基本达到稳定,优化后整体可靠度由0.728 123提高到0.891 355,优化率达22.4%。2)外脊索、内脊索、外斜索、内斜索及外环索杆件面积分别增大了1.35%、9.33%、1.33%、11.99%和6.70%,内压杆、外压杆及内环索杆件面积分别减小20.0%、17.36%和1.34%,该变化现象总体上与前面参数分析时各类杆件截面变化对于结构可靠度的影响规律相一致。3)文中同时计算分析了结构质量不约束时截面优化设计后结构整体可靠度为0.998 795,优化率达37.2%,即优化过程中无质量约束可进一步提高结构可靠度。 图3 截面优化迭代过程Fig. 3 Iterative process of cross section optimization 表3 截面优化前后不同杆件截面积及可靠度Table 3 Different bar cross-sectional area and reliability before and after section optimization 通过分析可以发现,该Geiger型索穹顶结构整体冗余度较低,各个子系统及子系统内的杆件均以串联的逻辑联结在一起,以至于结构中微小的损伤会较大程度地影响整体可靠度,因此,文中以改变子系统内杆件的逻辑联系、提高整个结构的冗余度为布索方案优化设计出发点,将原结构外圈径向布置的外脊索和外斜索布置方式调整为Levy型,杆件面积为原杆件面积0.6倍,形成内圈Geiger-外圈Levy型的复合型索穹顶。优化后的结构模型如图4所示。 可以发现,外脊索与外斜索的杆件数均由16根增加到了32根。根据Maxwell准则,该结构的冗余度r=b+k-3j=176+3×16-3×64=32,与优化前的模型比较,其冗余度大幅提高。重新计算布索方案优化后各类杆件的可靠度及结构整体可靠度,计算结果见表4,可见:1)对结构布索优化方案进行调整后,结构整体可靠度由0.728 123提高至0.862 487,优化率达18.5%。2)对布索优化方案进行调整后,结构整体自重略微增加,虽然大部分杆件的可靠度并无明显的变化,但由于结构整体冗余度大幅提高,各子系统内部联结逻辑也发生了改变,以至于结构整体的可靠度明显提高,因此该方案是一种可行、有效的优化方案。3)作者同时研究了其他提高结构冗余度的布索优化方案,发现同样可有效提高结构可靠度。 (12) 优化迭代过程如图5所示,优化结果如表5所示,可见,1)优化迭代到180次后基本达到稳定,截面优化后结构整体可靠度由0.862 487进一步提高至0.997 676,优化率达15.7%。2)优化后,外斜索和压杆类杆件截面减小,其余各类杆件截面积均增大。其中,外压杆和内压杆的截面变化最大,均达到杆件截面变化临界值-20%;其次为内斜索、内脊索、内环索和外斜索,分别为17.3%、12.0%、12.0%和-12.0%;外脊索和外环索的截面变化最小,分别为6.7%和9.4%。3)文中同时计算分析了优化过程中不控制结构质量时优化后结构整体可靠度为0.999 630,优化率为15.9%。 图5 质量约束布索-截面综合优化迭代过程Fig. 5 Iterative process of mass constraint cable-cross section synthesis optimization 表5 质量约束布索-截面综合优化前后不同杆件截面积及可靠度Table 5 Different cross sectional areas and reliability of bars before and after mass constrained cable-section optimization 文中针对索穹顶结构缺乏有效的基于结构性能优化设计理论现状,以可靠度理论为基础,提出了基于一次二阶矩理论中心点法的索穹顶结构非线性可靠度分析方法,并结合Geiger型索穹顶模型开展了结构可靠度分析、截面优化设计、布索优化设计及布索-截面综合优化设计等,得出如下结论: 1)不同类型杆件截面面积的变化,导致结构整体可靠度呈现出不同的变化趋势; 2)控制结构质量不增加前提下,索穹顶结构截面优化后,结构可靠度由0.728 123提高到0.891 355,优化率为22.4%; 3)布索方案优化使结构可靠度由0.728 123提高至0.862 487,优化率为18.5%; 4)控制结构质量不增加前提下,对索穹顶结构进行布索-截面综合优化,结构整体可靠度由0.862 487进一步提高至0.997 676,优化率为15.7%,因此开展合理的截面优化和布索优化设计可有效提高结构整体可靠度。 综上,文中基于可靠性的分析、评价及优化设计理论具有一定的理论研究和工程应用价值。2 索穹顶结构可靠性分析
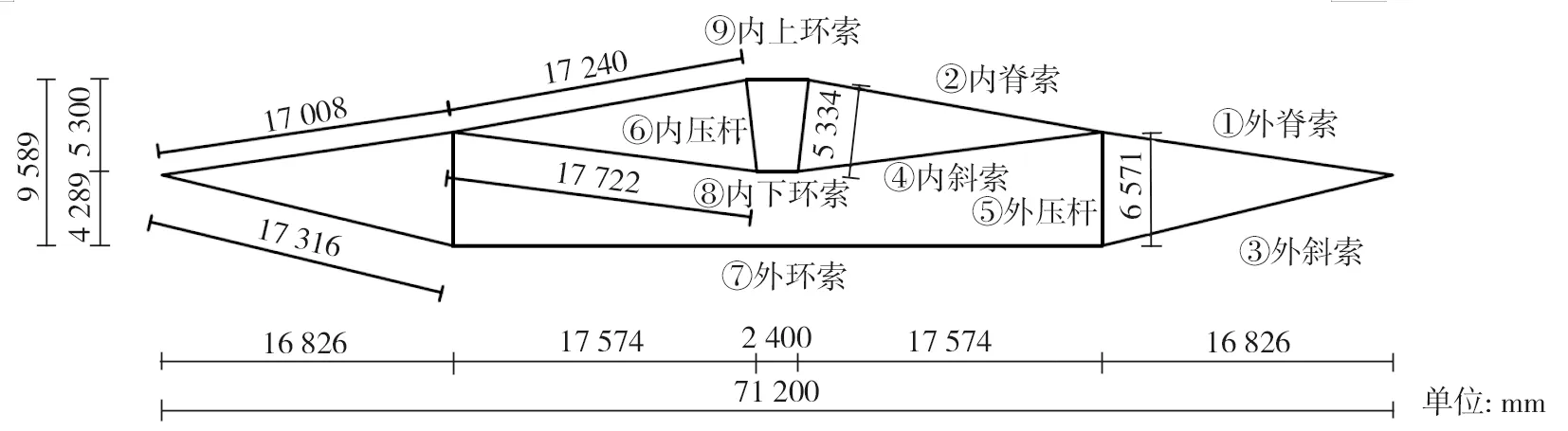
3 截面优化设计
3.1 优化算法
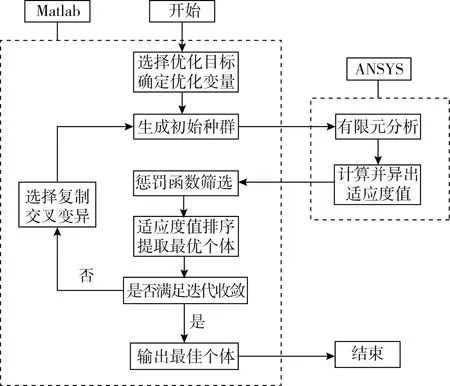
3.2 优化模型
3.3 优化结果
4 布索方案优化设计
5 布索-截面综合优化设计
5.1 优化模型
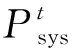
5.2 优化结果
6 结语

