新型可恢复功能组合柱设计及其抗震性能研究

马 高,王择文

(1. 湖南大学 土木工程学院,湖南 长沙 410082; 2. 工程结构损伤诊断湖南省重点实验室(湖南大学), 湖南 长沙 410082)

0 引言

目前我国建筑结构抗震设计需满足“小震不坏,中震可修,大震不倒”[1]的设防目标。然而,在我国的唐山、汶川、玉树等重大地震事件中,大量建筑遭受了超过自身设防烈度更大的地震作用,发生倒塌破坏,使人民生命财产安全受到严重损害。且部分未倒塌的建筑,由于结构非线性变形引起的损伤和残余位移过大而不能被修复使用,震后的拆除重建造成显著的经济损失。故建筑结构需要具有可恢复功能,即在震时保持一定的功能水平,震后能被快速修复,以减少经济损失,保障社会稳定。当结构柱采用可恢复功能柱时,在强震作用下,柱身残余变形小且柱端可以进行修复,则震后结构便能实现功能可恢复。

目前,可恢复功能柱主要分为2类:预应力摇摆柱[2-4]和形状记忆合金(shape memory alloy,SMA)可恢复柱[5]。预应力摇摆柱通常联合使用预应力筋和预制耗能部件,比如角钢[2]、耗能钢筋[4]、摩擦装置[6]等。此类柱受震时发生摇摆,耗能和损伤集中在耗能部件,预应力和自重使其能一定程度复位,但实际应用时预应力施工较复杂,且会增加构件轴压比,从而减小延性。SMA可恢复柱在塑性铰区使用SMA棒材作为纵筋[5],并确保SMA与钢筋连接可靠。SMA材料的超弹性特性能使柱在震后实现自复位,震后修复柱端保护层混凝土即可恢复其使用功能。由于SAM材料成本高,限制了此类柱的推广使用。

近年来,国内外学者提出在柱中配置低黏结高强钢筋,其应变弹性段宽、与混凝土黏结力小,受力后与混凝土可产生滑移,使纵筋轴向应力沿其长度方向分布均匀,易于纵筋保持弹性,从而提升柱变形后的自复位能力。叶列平等[7]将柱纵筋替换为钢绞线,并对结构进行非线性动力时程分析,发现框架柱端无塑性铰发展,震后结构残余变形小,结构损伤集中在框架梁端。张鑫等[8]对1/2缩尺的三层两跨混凝土框架进行低周往复加载,结果显示钢绞线混凝土框架底层柱底端纵筋屈服延迟,各层残余位移比钢筋混凝土(reinforced concrete,RC)框架小。SUN等[9]对高强螺纹钢筋混凝土柱进行低周往复加载,在0.5的高轴压比下柱残余变形仍较小。刘志华等[10]对钢绞线混凝土圆柱进行拟静力试验,结果表明,钢绞线混凝土柱相比于RC柱承载力提高90%,且位移角达6%时残余位移角不到2%。由于传统的钢绞线混凝土柱耗能效果差,且在经受一次地震后,纵筋滑移会使抗侧刚度减小,修复难度大,无法保证其二次抗震性能。

基于此,文中提出应用钢绞线的新型可恢复功能组合柱(简称新型可恢复柱)构造方法,该柱具有良好的自复位能力和耗能能力,且震后易于修复。基于文献[13]中试验建立可恢复柱的有限元分析模型并验证模型可靠性,对比研究可恢复柱与传统钢筋混凝土柱和钢绞线混凝土柱的抗震性能;建立6层典型框架结构,采用Pushover及动力时程分析系统研究应用该新型可恢复柱框架结构的塑性铰分布规律以及残余位移控制效果,计算并比较应用不同类型柱框架结构的地震易损性和可恢复性。

1 新型可恢复功能组合柱构造

新型可恢复柱构造如图1所示,柱截面配有钢绞线和普通钢筋,二者布置比例可根据设计调整;柱塑性铰上部设置超高性能混凝土(ultra high performance concrete,UHPC)加高段,以限制钢绞线的滑移[11];柱底部置换区核心区为UHPC浇筑,核心区底部套有钢盒,布置完耗能钢筋后在核心区四周再浇筑UHPC,过渡区钢盒将其与柱身UHPC加高段分开,且核心区通过缠绕胶带与四周UHPC相分隔,以使柱可绕核心区钢盒侧边摇摆;底部置换区的钢绞线用PVC管包裹,使其与UHPC无黏结;底段截面中部的预制耗能钢筋套有钢套筒以防止其受压屈曲,提高耗能能力,其两端与柱身钢筋用螺纹套筒连接,耗能钢筋材料与柱身钢筋相同,直径小于柱身钢筋,可实现耗能钢筋屈服而柱身钢筋保持弹性;钢绞线端部设锚固钢板,钢绞线在钢板外侧用挤压锚挤压锚固,以限制钢绞线端部滑移;柱底端设置开槽钢底板,以限制核心区钢盒水平移动。

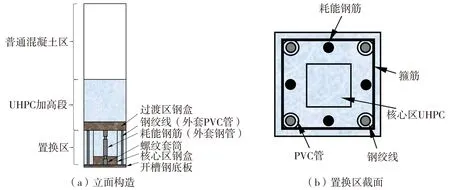
图1 新型可恢复柱构造图Fig. 1 Schematic diagram of new resilient column

该新型可恢复柱抗震工作机理为:小震下,柱处于弹性状态;中震及大震下,柱底部绕核心区钢盒侧边产生摇摆转动,核心区四周的UHPC只承受压力,同时剪力通过槽口传向底板;由于钢绞线屈服应变高,且钢绞线在柱底置换区段与UHPC无黏结,其应力沿长度均匀分布,屈服延缓,故其自身的弹性恢复力与柱顶竖向轴力使柱复位;耗能钢筋发生屈服耗能,而上柱柱身保持弹性,并且即使无黏结钢绞线屈服,因其在此区段钢绞线容易压弯,对柱残余变形影响小。因此,该新型柱震后只需替换置换区受损的耗能钢筋和核心区四周的UHPC即可完成修复。

2 有限元模型建模与验证

2.1 模型信息

采用文献[12]中现浇钢筋混凝土柱(1#试件)、现浇钢绞线混凝土柱(3#试件)和文献[13]中底段应用无粘结钢绞线和可替换耗能钢板的外张拉式自复位方钢管混凝土柱脚SCCB-1试件的实验结果,验证有限元软件OpenSees建模的正确性。1#试件与3#试件轴压比为0.25,SCCB-1试件轴压比为0.2,钢绞线初始预拉力为110 kN,耗能钢板截面积为320 mm2,柱尺寸及配筋如图2所示。

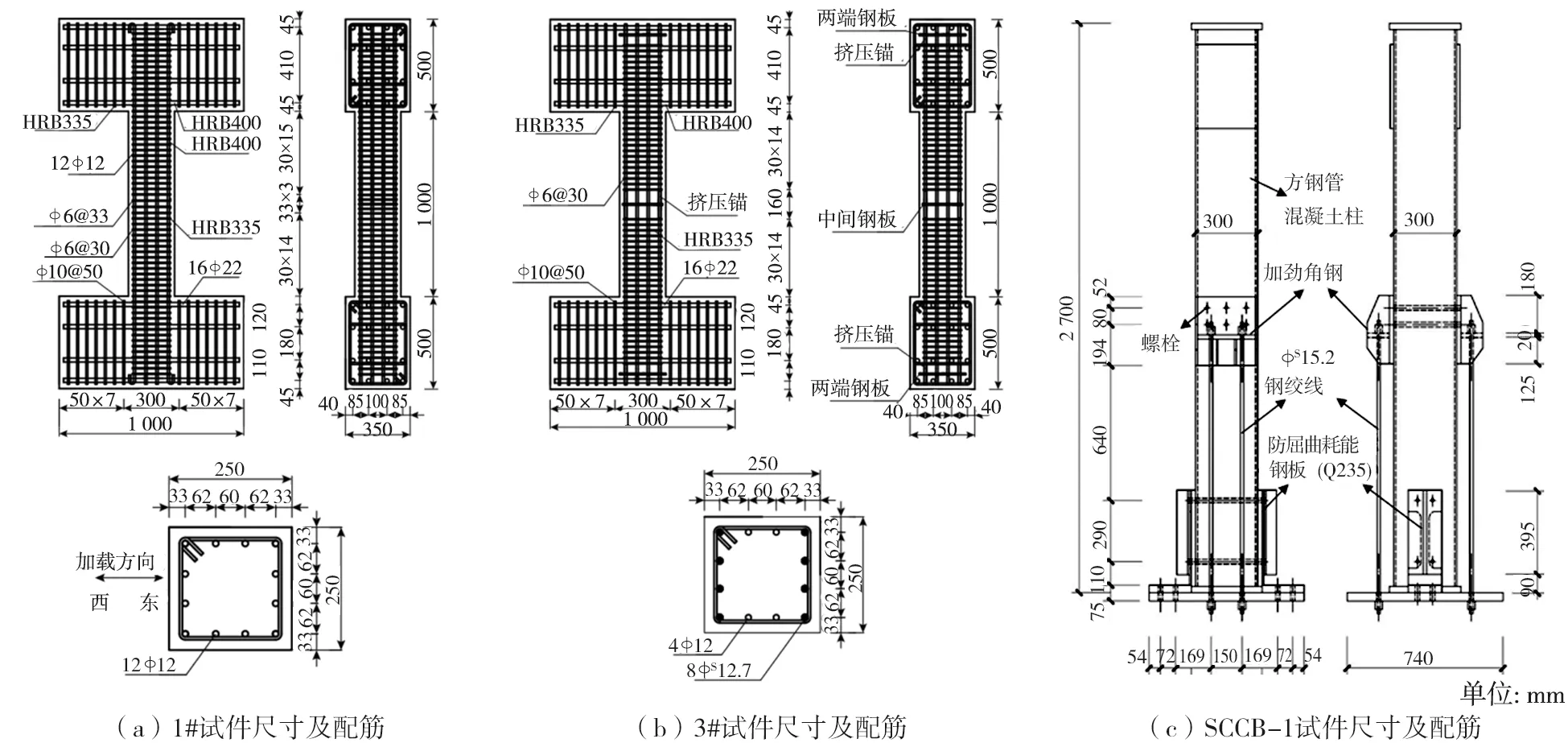
图2 试件尺寸及配筋信息Fig. 2 Specimen size and reinforcement information

柱截面采用纤维截面,使用dispBeamColumn单元进行模拟,钢材本构模型采用Steel02,混凝土本构模型采用Concrete01,箍筋约束混凝土的参数计算采用Kent-Park模型。WANG等[14]对比配不同种类钢筋试验柱的纵筋全长应变分布,发现变形钢筋的应变集中在柱端部,而超高强螺旋钢筋的应变沿柱高具有近似均匀的分布,意味着更多截面的纵筋参与抵抗拉力,即纵筋产生滑移,并在有限元建模时修正了纵筋弹性模量,由式(1)～式(6)计算,表1给出了3#试件钢绞线的修正弹性模量计算结果。SCCB-1试件中外张拉预应力钢绞线采用ElasticPP本构模型,设定初始应力,并不考虑其受压性能。

表1 3#试件修正弹性模量的计算Table 1 Calculation of modified elastic modulus of specimen 3#

Esm=fy/εym

(1)

εym=εy+Sslip/Lemd

(2)

(3)

(4)

(5)

(6)

式中:εym为钢筋的修正屈服应变;εy为钢筋的原始屈服应变;Sslip为钢筋屈服时的钢筋黏结滑移;Lemd为钢筋的预埋锚固长度;Esm为修正杨氏模量;fy为钢筋的屈服强度;εs0为钢筋端部的轴向应变;fc为混凝土抗压强度;ld为钢筋屈服时的延伸长度;db为钢筋直径;lAL,Column为柱内的基本锚固长度;u为钢筋的黏结强度。

2.2 模型验证

由图3可知,1#试件、3#试件和SCCB-1试件的模拟结果与试验结果吻合良好,故利用对应的单元和材料本构进行OpenSees建模可以有效预测钢筋混凝土柱、钢绞线混凝土柱和新型可恢复柱的抗震性能。

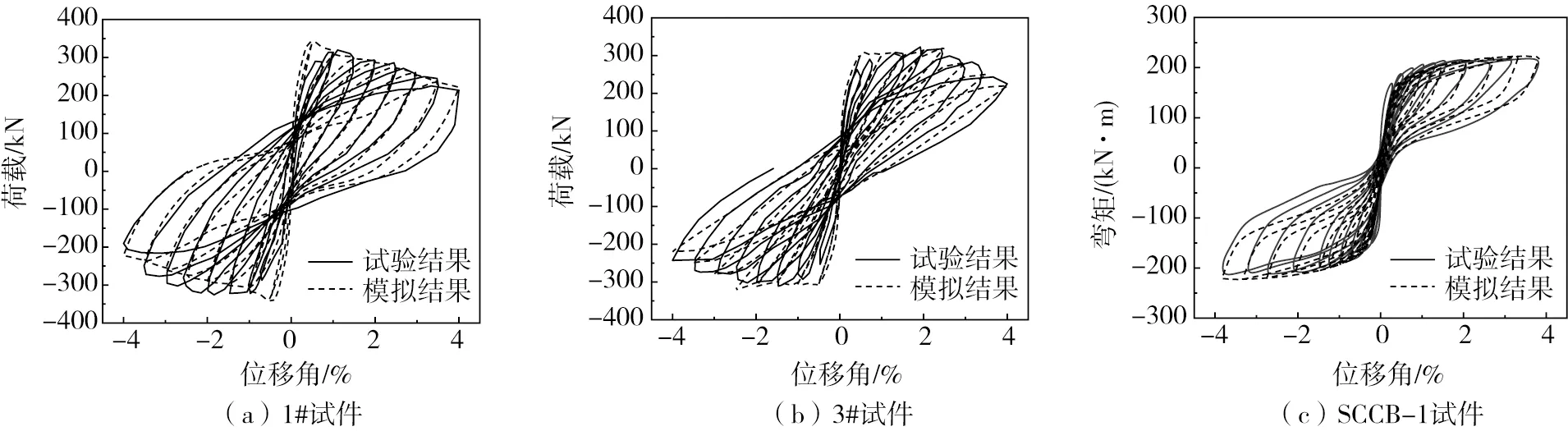
图3 模拟结果与试验结果对比Fig. 3 Comparison between simulation results and test results

3 新型可恢复柱抗震性能参数分析

3.1 分析模型

为深入研究新型可恢复柱的抗震性能,采用OpenSees建立新型可恢复柱的单柱模型,并进行低周往复加载。柱构件尺寸、配筋参考图2(b)的3#试件,2%钢掺量的UHPC的抗压强度与抗拉强度分别取146.8和6.7 MPa[15]。柱沿柱高方向采用6个基于位移的梁柱单元。新型可恢复柱置换区PVC管包裹的钢绞线初始应力为0,故可直接采用ElasticPPGap本构模型,不考虑其受压性能,并将gap值设为0。其余钢绞线及普通钢筋本构模型均选用Steel02。普通混凝土选用Concrete01本构模型,UHPC单轴受拉[15]和单轴受压[16]本构模型符合ECC01,箍筋约束混凝土特征点参数同样采用Kent-Park模型计算。

为研究置换区高度和截面钢绞线配置率对新型可恢复柱抗震性能的影响,设置5种新型可恢复柱工况(KHF1～KHF5),柱身UHPC段总高350 mm,并取文献[12]中1#和3#试件的试验结果作为对比,各试件参数及性能指标如表2所示。

3.2 抗震性能分析

结合表2、图4(a)可知,3#试件在最大水平位移下残余位移角相比1#试件减小56.3%,但耗能能力为1#试件的72%,而KHF1具有更大的侧向刚度,其水平承载力是1#试件的1.7倍,残余位移最小,且耗能能力增长6.3%。图4(b)表明,KHF3相比KHF1水平承载力提高8.4%,耗能能力降低7.2%,这是由于随置换区高度增加,即钢绞线无黏结段增长,导致钢绞线和耗能钢筋的屈服被延缓,耗能能力变差,同时柱屈服截面上移,使其水平承载力增加。由图4(c)可知,KHF5相对KHF4的耗能能力提升30.7%,承载力下降24.9%,残余位移增加2.5倍。而KHF2与KHF4的承载力及残余位移角相差不大,这是由于平行于加载方向截面中部的钢绞线距离中性轴较近,性能发挥不充分,说明垂直于加载方向的截面各边的钢绞线配置率对柱抗震性能有重要影响。综上,在设计新型可恢复柱时,其置换区高度要依据承载能力和耗能需求综合确定,且要保证垂直于加载方向截面各边的钢绞线配置率。

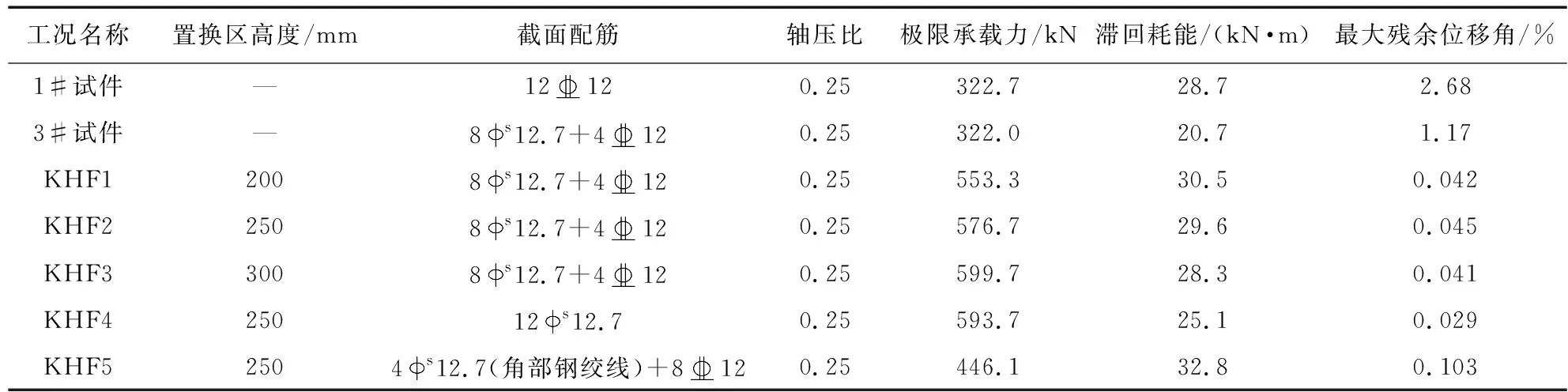
表2 试件参数及性能指标Table 2 Specimen parameters and performance indexes

图4 各工况滞回曲线Fig. 4 Hysteretic curve under various working conditions

4 算例设计及静力弹塑性分析

4.1 框架结构算例设计

为深入研究应用该新型可恢复柱框架的抗震性能,不失一般性,文中选取6层3跨的典型多层框架结构作为研究对象。框架结构的平面长度为29.3 m,宽度为14.9 m,首层层高为3.9 m,其余层层高为3.3 m,结构总高度为20.4 m,其平面图及立面图如图5所示。采用PKPM分别设计7度(0.1 g)设防RC框架(简称Frame1)和8度(0.2 g)设防RC框架(简称Frame2),设计地震分组为第2组,Ⅱ类场地,阻尼比为0.05,地面粗糙度C类;楼面活载2 kN/m2,屋面恒荷载7 kN/m2,楼面恒荷载4.5 kN/m2,基本风压0.4 kN/m2;柱截面尺寸500 mm×500 mm,梁截面尺寸为250 mm×500 mm,梁柱主筋采用HRB400,混凝土选用C40。按照等面积替换的方法用φs17.8钢绞线仅替换Frame1柱中全部纵筋,建立钢绞线混凝土框架(简称Frame3)。同时建立采用新型可恢复柱的可恢复框架(简称KHFframe),如图5(c)所示,对每层柱反弯点上下均使用新型可恢复柱构造,置换区高度应大于Frame1柱铰区高度,塑性铰区高度Lp采用式(7)计算[17]:

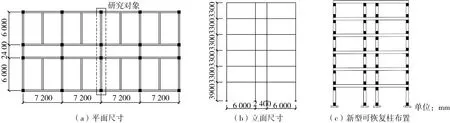
图5 RC框架模型示意图Fig. 5 Schematic diagram of RC frame

Lp=0.08L+0.022dbfy

(7)

式中,L、db、fy分别为柱高、纵筋直径和其屈服强度。

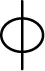
表3 框架配筋信息Table 3 Frame reinforcement information mm

间距为200 mm。

4.2 静力推覆分析

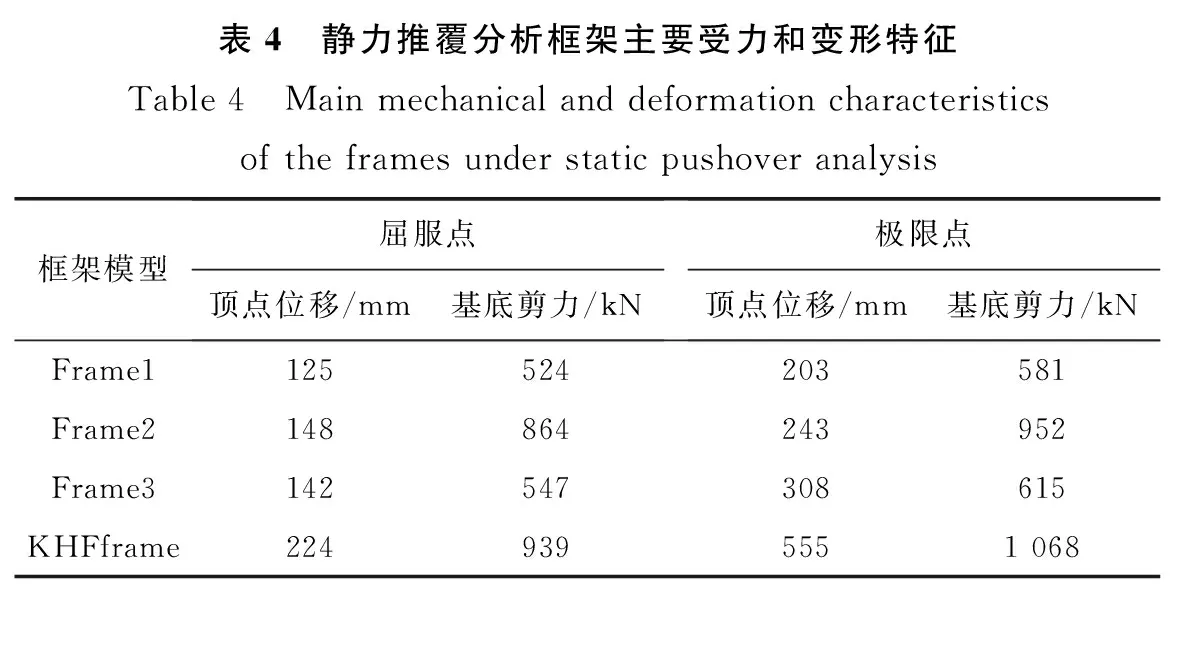
采用OpenSees对上述4种框架建立有限元模型,截面采用纤维模型,梁柱采用基于位移的梁柱单元,考虑P-Delta效应,不考虑节点剪切变形,每根柱划分6个单元,每根梁划分5个单元。对结构侧向施加倒三角荷载,并采用位移加载方式,对其进行Pushover分析,其顶点目标位移设为612 mm(3%),得到结构的顶点位移-基底剪力推覆曲线。由图6和表4可知:Frame3由于柱中钢绞线的弹性模量修正后减小,屈服位移比Frame1高13.8%,达到峰值承载力时的位移比Frame1高51.7%,并且其抗侧承载力达到最大后退化相对缓慢,延性增强。KHFframe的抗侧刚度小于Frame2,屈服位移是Frame2的1.6倍,原因是KHFframe应用了可恢复柱,其底段纵筋应力在可置换区段内均匀分布,应力增长慢。并且由于柱端混凝土采用UHPC,具有良好的抗压变形能力,KHFframe的抗侧承载力达到最大后无明显退化。

4.3 塑性铰分布规律

结构推覆至3%总高度时结构塑性铰分布情况见图7,其中塑性铰数值为构件端部塑性铰截面的曲率,4种框架均形成了“强柱弱梁”机制。Frame1和Frame2底层柱底端出现塑性铰,并且低楼层梁端塑性铰发展充分;Frame3结构柱无塑性铰发展,KHFframe底层柱底端及上层少数柱端出现微弱塑性铰,即耗能钢筋开始屈服,弱柱端塑性铰可以有效地推迟框架的侧向倒塌;Frame3和KHFframe的梁端塑性铰发展均较Frame1减弱,减轻了结构的地震损伤。此外,Frame3与KHFframe的最终破坏由低层梁端塑性铰充分发展导致,以致钢绞线混凝土柱和新型可恢复柱的抗震性能未充分发挥,但这可为结构提供一定的性能冗余。

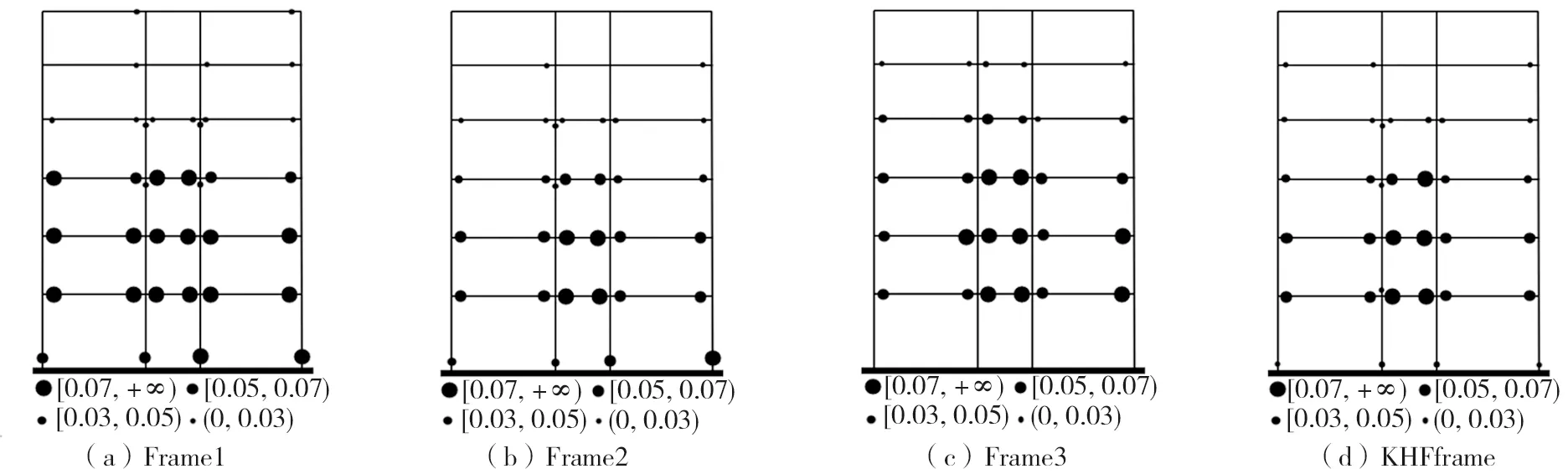
图7 框架塑性铰分布Fig. 7 Distribution of plastic hinges of frames

5 可恢复框架非线性动力时程反应

5.1 层间位移响应

为研究框架在真实地震波下的反应,对4类框架进行动力时程分析。在PEER数据库中选取20条Ⅱ类场地对应的地震动记录,并将PGA调幅为220 cm/s2,对结构进行非线性动力时程分析(以下简称动力时程分析)。图8为结构在各条地震波下的层间最大位移角与残余位移角,图中横线代表结构在20条地震波下位移反应的均值。Frame2的最大层间位移角均值最小,其原因是Frame2为8度抗震设防,而动力时程分析中地震波的PGA为220 cm/s2。Frame3的最大层间位移角均值最大,主要原因是钢绞线的低黏结效应导致其侧向刚度最小。KHFframe的最大层间位移角均值小于Frame1和Frame3,且其残余位移角均值最小,为0.095%,较Frame1降低57%,可修复概率最大。图9(a)所示,KHFframe的残余层间位移角均值为0.27%,为4类框架最小,Frame2次之,为0.30%。图9(b)为结构层间残余位移角与最大位移角的比值(以下简称层间残余位移比值)分布,KHFframe对应比值的均值最小(0.12),较Frame1降低49%,自复位性能最好。

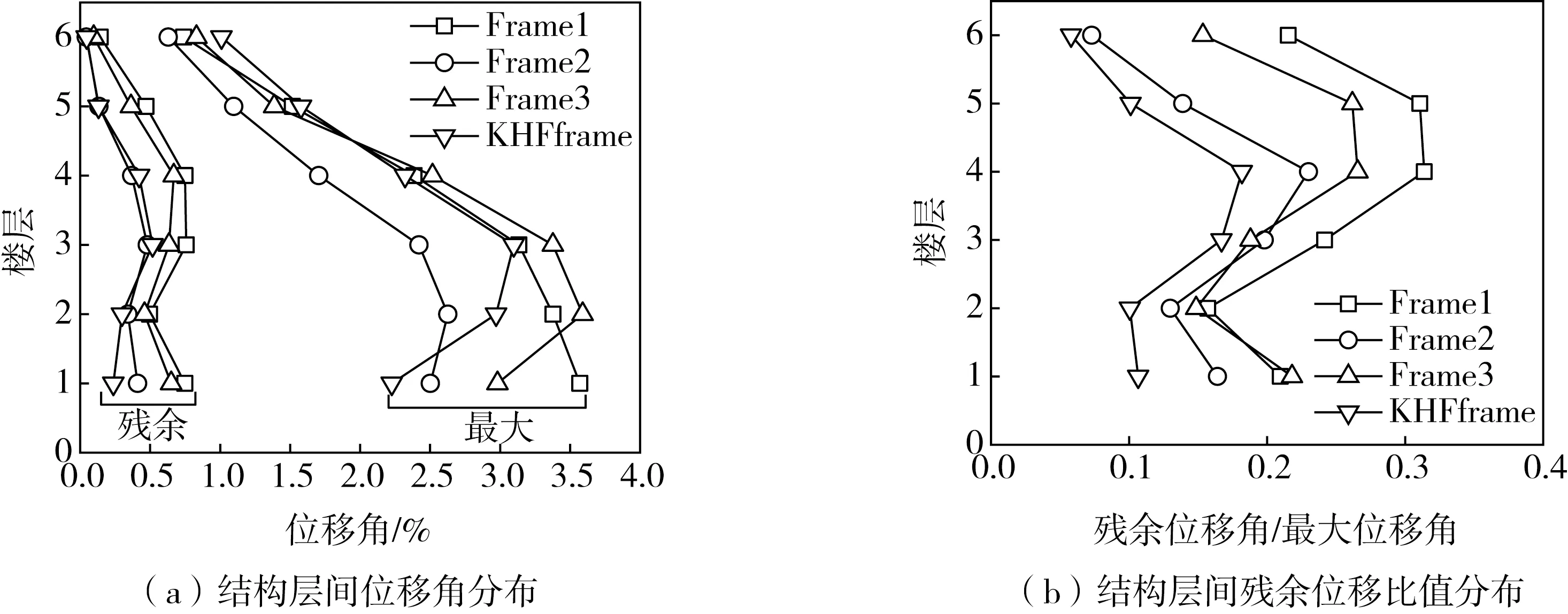
图9 结构在地震激励下的层间位移响应Fig. 9 Inter-story displacement responses of frame structure under seismic excitation

5.2 残余层间位移控制效果分析

以KHFframe为例,绘制其最大层间位移角与残余位移角的关系曲线。图10(a)为20条地震波下各层的位移响应集合,取其中值可得到图10(b)所示趋势线。由图10(b)可知:当最大层间位移角超过0.22%时,结构发生屈服并开始出现残余位移,但可控制在0.02%以内,直至最大层间位移角达到1.32%;超过1.32%后,残余层间位移角开始显著增长。图11(a)给出了4种框架的中值曲线,Frame1、Frame2和Frame3对应的2个阈值分别为:0.26%、0.63%;0.23%、0.72%;0.30%、0.89%。KHFframe的后阈值最大,在超过此阈值后,KHFframe的残余位移增长最缓,且在最大位移角为2.0%时,其残余位移角依然小于0.2%,说明其在经历大震后的可修复性最强。图11(b)为最大层间位移角与层间残余位移比值关系的中值曲线,Frame1、Frame2和Frame3对应的曲线初始就有缓慢增长,而KHFframe对应的曲线初始为明显的平台段,在最大位移角超过1.29%之后才有明显的上升趋势,表明KHFframe在小中震作用下具备稳定的的自复位能力,且在最大层间位移角为2.0%时,其层间残余位移比值相对Frame1降低58%,说明KHFframe在大变形下依然具有很强的自复位性能,Frame3次之。

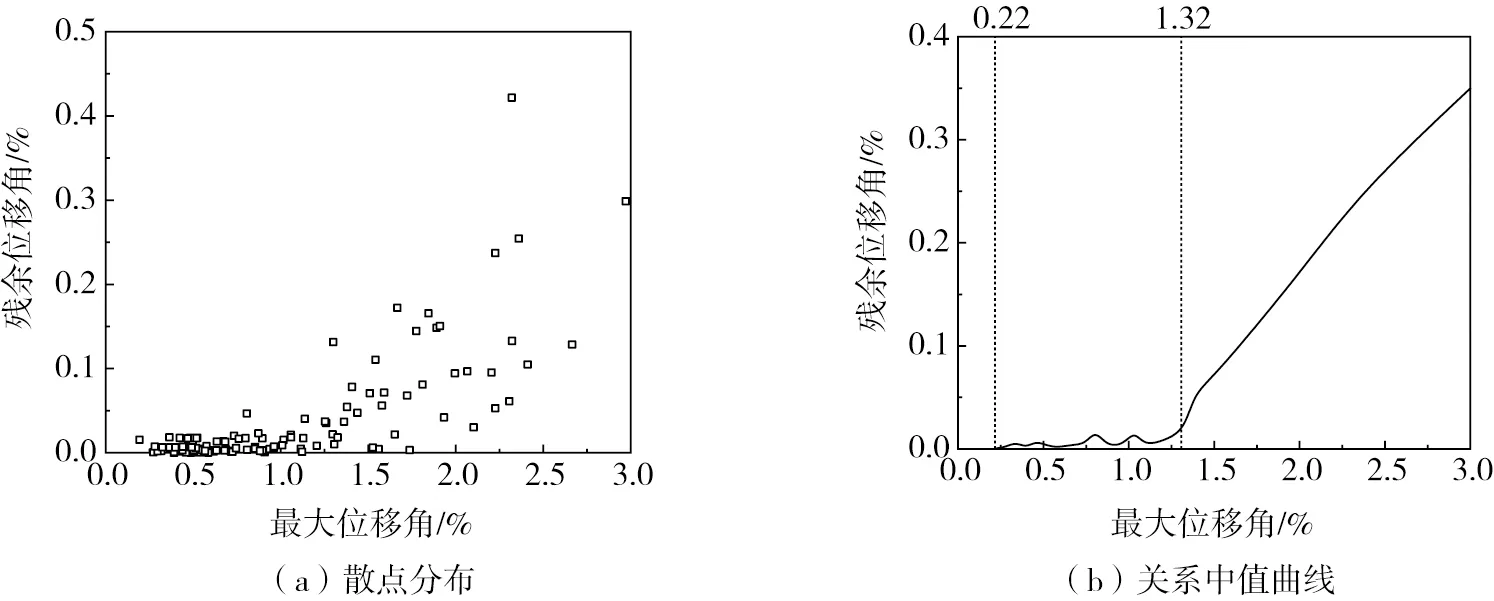
图10 KHFframe最大层间位移角与残余位移角的相关性Fig. 10 Correlation between the maximum drift ratio and residual drift ratio of KHFframe

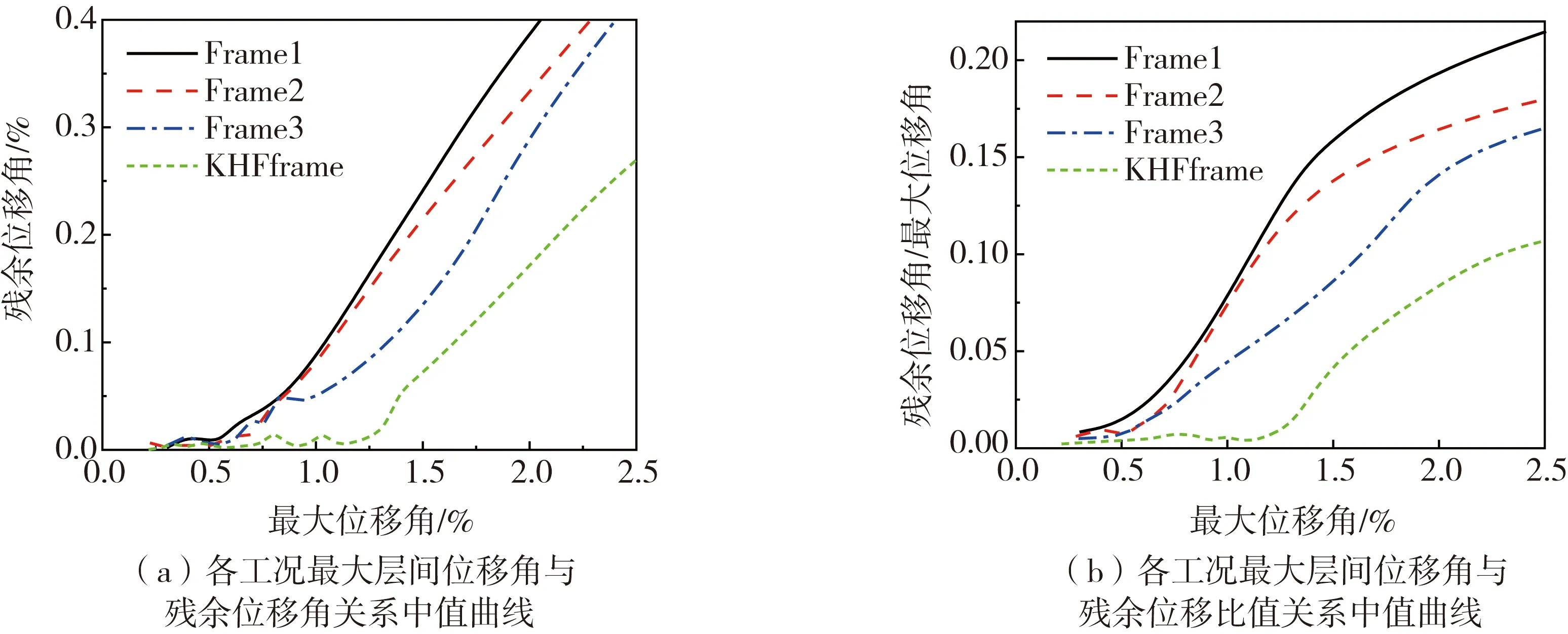
图11 框架位移指标关系曲线Fig. 11 Frame displacement index relationship

6 可恢复框架地震易损性与可恢复性评价

6.1 地震易损性分析

结构的地震易损性是指给定结构不同地震动强度,其达到或超过某损伤极限状态的概率。假设需求参数和谱加速度Sa存在对数线性关系,进行结构易损性分析[18],得到结构在不同谱加速度下不同性能水准的超越概率,如式(8)所示:

(8)

图12所示,KHFframe 3种极限状态下的易损性曲线均在4种框架的最右侧,即同等地震强度条件失效概率最低。此外,Frame3的易损性曲线相对于Frame1向右偏移,说明钢绞线的应用亦提高了框架抗震性能。

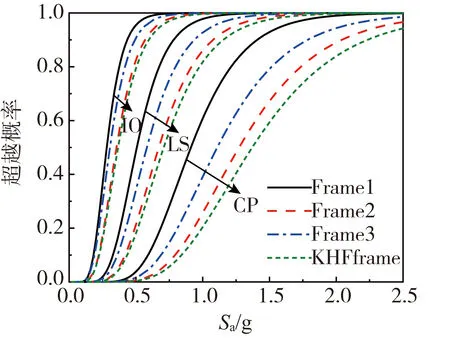
图12 结构易损性曲线Fig. 12 Seismic fragility curve of frames

6.2 可恢复性评价

6.2.1 可恢复指标

结构可恢复性是指结构在遭遇地震作用时,有较高的抗震冗余度,并且其使用功能能够被快速恢复至震前水平的性能,其示意图见图13。通过式(9)[19]可以对给定损伤状态下结构的可恢复性进行量化计算,得到可恢复指标Rj:

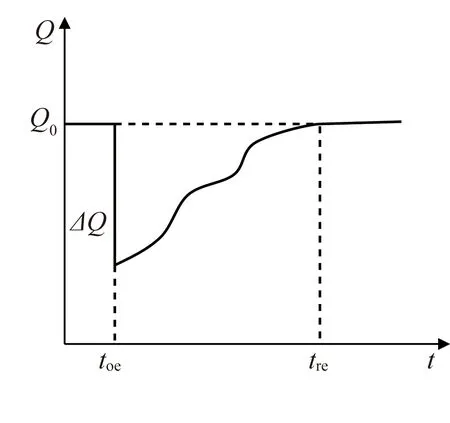
图13 结构可恢复性示意图Fig. 13 Schematic diagram of resilience of structure

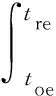
(9)

式中:Qj(t)为功能函数,由式(10)表示[20]:

Qj(t)=Qres+(1-Qres){H(t-toe)-H[t-(toe+tre)]}frec(t)

(10)

式中:j=1、2、3、4分别代表轻微损伤、中等损伤、严重损伤以及完全破坏,其对应的层间位移角分别为(0, 1%]、(1%, 2%]、(2%, 4%]以及(4%, +∞];Qres为灾后结构的剩余功能值[19];H(t)为赫维赛德阶跃函数;frec(t)为恢复函数,分为负指数函数型,余弦函数型和正指数函数型[20],分别用式(11)～式(13)表示:

frec(t)=1-exp{-k[(t-toe)/tre]}

(11)

frec(t)={1-cos[π(t-toe)/tre]}/2

(12)

frec(t)=exp{-k[1-(t-toe)/tre]}

(13)

结合结构易损性分析结果,通过式(14)可得到在不同谱加速度下结构的可恢复性指标R(Sa)[21]。

(14)

式中:Pj(Sa)为给定谱加速度下结构发生j损伤的概率,见式(15):

(15)

式中,Pf,1(Sa)、Pf,2(Sa)、Pf,3(Sa)以及Pf,4(Sa)分别为结构轻微损伤、中等损伤、严重损伤以及完全破坏的超越概率。

图14所示为4类框架可恢复性指标随谱加速度的变化曲线。在初期,随着谱加速度逐渐增大,框架可恢复指标下降缓慢,而当谱加速度超过一定值后快速下降,即结构地震损伤开始显著发展。在相同谱加速度下,KHFframe的可恢复性最好,表明应用新型可恢复柱后,普通RC的抗震可恢复能力大幅提升。当谱加速度为0.40 g时,Frame1、Frame2、Frame3和KHFframe的可恢复性指标分别为0.66、0.76、0.69以及0.78。为了反映给定地震动强度下可恢复性指标的离散性,图15给出了KHFframe在谱加速度为0.30、0.40以及0.50 g下的可恢复性概率密度分布,可以看出谱加速度越大,概率分布越离散,说明谱加速度越小,可恢复性指标对结构可恢复性的量化越准确。

6.2.2 可恢复性指标增长量化分析

为量化分析该新型可恢复柱应用后结构可恢复性提升的效果,文中采用可恢复性相对增长率Rrela(Sa)指标,其表达式如式(16):

Rrela(Sa)=[Rkhf(Sa)-R1(Sa)]/R1(Sa)

(16)

式中:R1(Sa)、Rkhf(Sa)分别为Frame1和KHFframe的可恢复性指标。图16为KHFframe相对Frame1的Rrela(Sa)超越概率,谱加速度越大,Rrela(Sa)越大,即新型可恢复柱在结构经受大震时的性能发挥越充分,在谱加速度为0.4 g时其可恢复性指标相对增长率平均值可达到30%。在给定的地震动下,Rrela(Sa)越大,其超越概率越小,故在可恢复框架设计时要确定保守的相对增长率。

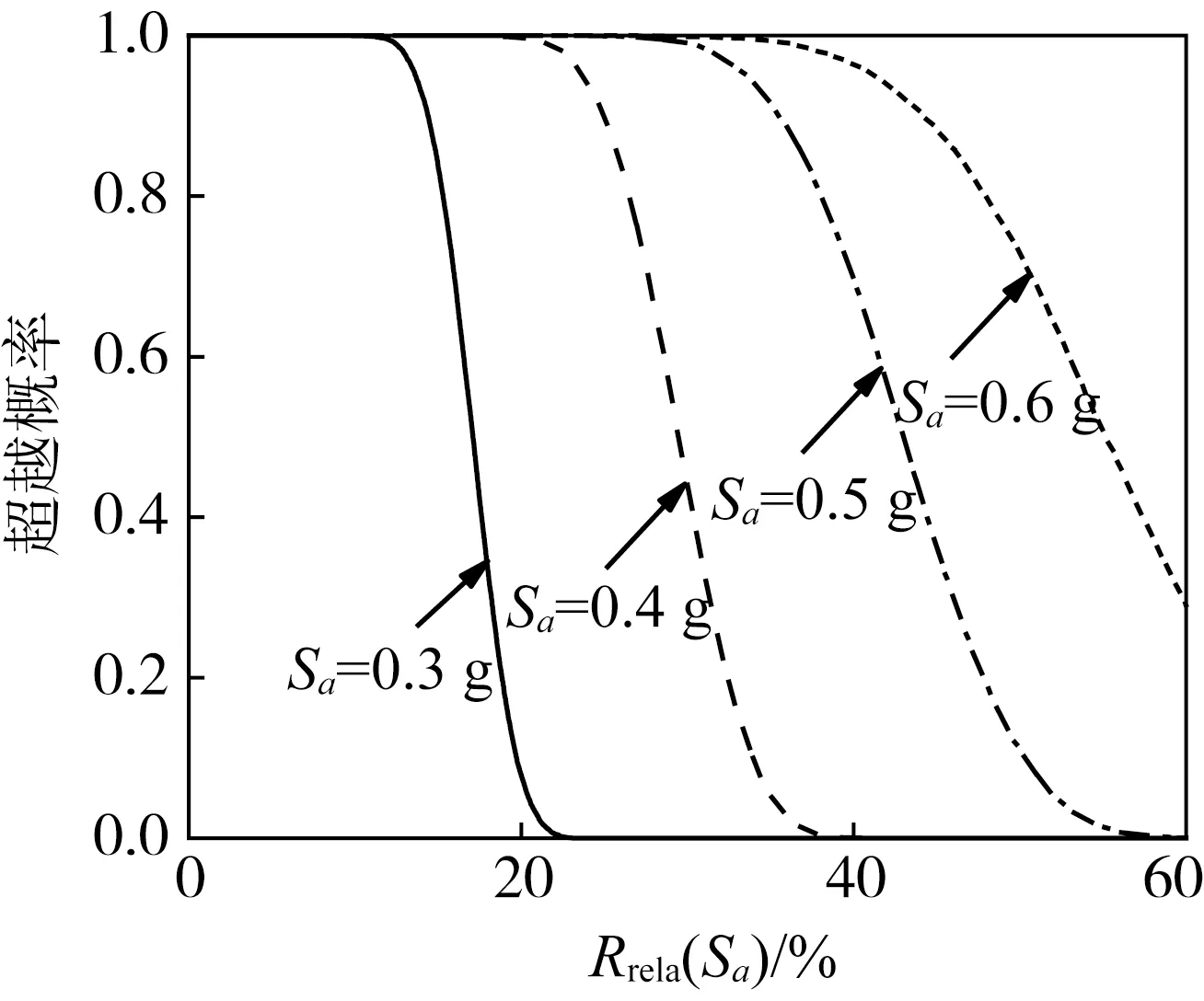
图16 KHFframe相对增长率的超越概率Fig. 16 Exceeding probability of relative growth rate of structural resilience of KHFframe

7 结论

文中提出了一种新型可恢复功能组合柱,该柱在地震作用下塑性变形集中在耗能钢筋,有良好的自复位能力,且震后易于修复,通过对比分析单柱及应用该柱的框架结构与普通结构的抗震性能,可获得如下结论:

1)新型可恢复柱抗震性能参数分析表明,增加置换区高度,可恢复柱耗能能力变差,水平承载力小幅度提升,但对其自复位性能无明显影响;钢绞线配置率增加,柱水平承载力和自复位能力提升,耗能能力下降明显。

2)7度设防RC框架应用新型可恢复柱后,抗侧能力显著提高,且高于8度设防RC框架,其达到水平承载力峰值后无明显退化。可恢复框架的破坏是由低层梁端塑性铰充分发展导致,说明新型可恢复柱性能未充分发挥,可为结构提供一定的性能冗余。动力时程分析表明,新型可恢复柱使框架的层间残余位移角及层间残余位移比值降低,且可恢复框架在大变形下仍具有良好的可修复和自复位性能。

3)在罕遇地震作用下,可恢复框架CP状态失效概率比8度设防RC框架低了23%。4类框架中可恢复框架的可恢复指标最高,且随地震作用增大,其相对于普通RC框架的可恢复性指标相对增长率提高幅度越大,且在设计可恢复框架时需考虑保守的相对增长率。表明该新型可恢复柱增强了结构抵抗倒塌的能力,并明显提高了结构的抗震可恢复性能。