含软弱土层边坡稳定性分析的全局滑面自动搜索技术

(武汉工程大学 土木工程与建筑学院，湖北 武汉 430074)

1 概述

现有商业软件[1]在进行边坡稳定性分析时，一般采用滑面穷尽搜索算法，以获取全局最小安全系数及其临界滑面。在滑面选择上，有圆弧滑面、多段折线滑面及多次样条曲线滑面[2]。通常，这些商业软件能较好地处理边坡稳定性计算问题。但是，在面对具有软弱下卧层的边坡时，圆弧滑面假设在搜索时有可能无法找到全局临界滑面；多次样条曲线滑面一般是在圆弧极限滑面的基础上进行局部微调得到的；此外，除非完全指定折线段的空间组成，商业软件通常只能采用三段线搜索临界滑面，且折线滑面需要工程师进行事先的初步预估，大致选定临界滑面折点的可能位置及首尾折线倾角范围，整个计算过程存在明显的人为因素影响，效率不高。

Malkawi于2001年提出了多段折线临界滑面的Monte Carlo随机搜索技术[3]，其采用逐步逼近策略，在坡体地质较为简单时具备全自动全局搜寻功能。张鲁渝[4-5]将之改良后进行了各种边坡的随机转角及常值转角的稳定性分析计算，效果较好。白桃[6]也采用Monte Carlo随机搜索技术进行了边坡等线段及等角度稳定性分析计算，结果表明此方法在不太复杂土质边坡中应用效果良好。而一旦在复杂土质边坡中使用时，基于其从头至尾的扫描特性，扫描结果会依赖于初始滑面位置，易导致计算结果离散，使得滑面落入局部极值中。

为解决上述问题，笔者引入模拟退火法(SAA)这一全局极值解算方法，结合改进后的Monte Carlo随机搜索技术，采用Morgenstern-Price方法进行含软弱土层边坡滑面的全局自动搜索。

2 边坡安全系数计算方法

一般而言，在进行边坡稳定性的极限平衡法分析时，滑面条块都会在纳入边坡拐点坐标的情况下进行水平方向上的等分。但在进行多层边坡稳定性分析或者土体参数存在空间变异性时，条块等分在计算上反而存在不便的地方。白桃[7]进行了边坡截面四面形划分的稳定性计算分析，但是对于含不规则土层截面的边坡无法进行网格划分。三角形具备良好的网格适应能力，本文以三角形网格划分为例，进行边坡条块划分说明。图1为澳大利亚计算机应用协会(ACADS)发布的标准考题截面之一[8]。图1(b)为图1(a)在边坡坡脚的局部放大图。

提取多段折线滑面G(x)与边坡截面三角网格相交后的所有交点，其与多段折线拐点合并后按x坐标排序，就可以获得多段折线滑面条块划分点位。如图1(b)所示，G(x)上任意相邻交点(含拐点)i与j，其与顶面线S(x)之间的部分就构成一个单独的计算条块。i、j的中点O与S(x)之间的垂直距离设定为条块高度。对于分层土体，每个条块高度范围内的土体重量进行叠加计算。O点所在三角形网格的强度参数取定为条块底面的强度参数，用于滑块的稳定性计算。

图1 折线滑面条分法示意图Figure 1 Diagram of Slices Method using n-segment Polyline

对于圆弧/非圆弧滑面的安全系数计算，数学方程较为完备的是Morgenstern-Price方法。为利于程序编制，本文采用朱大勇提出的简明Morgenstern-Price法[9]。

3 边坡临界滑面的扫描算法

3.1局部搜索扫描算法

图2 局部临界滑面搜索扫描算法[6]Figure 2 Searching Strategy for Local Critical Slip Surface

图2为白桃[6]进行多段折线滑面的局部临界滑面扫描算法，其核心思想就是采用Monte Carlo随机方法进行等角/等边逐段搜索最优解的方法进行边坡稳定的分析计算。从步骤1至步骤8为一轮，经多轮扫描一般可获取均值边坡的极限滑面。在步骤2和步骤8中，采用等角度规避边坡地面线拐点，其余旋转步骤均采用等长线段旋转方式。这种方法存在明显的短板，即面对含多层软弱层土质边坡时，容易陷入局部极值的问题。文献[6]中有专门的论述。

3.2全局搜索扫描算法

3.2.1多段折线模拟退火法

为解决上述扫描中的局部极值问题，本文通过引入模拟退火法[10]。模拟退火法用于描述系统在温度t下从能量E(i)状态i进入具有能量E(j)状态j的机制。t随算法进程逐步递减，类似于固体退火过程中的温度角色。计算持续进行Metropolis算法：“产生新解—判断—接受/舍弃”的迭代过程，对应着固体在某一恒定温度下趋于热平衡的过程。模拟退火算法从某个初始解出发，经大量解的变换最终求得最优化问题的整体最优解。本文对每次局部扫描获得的极限滑面施加一定大小的抖动，以概率接受的方式进行全局极限滑面的位置筛选，计算流程见图3。

模拟退火法是一种全局近似算法，在温度下降过程中，系统接受恶化解的概率不断降低，直到退火温度后达到收敛解。在模拟退火的过程中，需要注意以下3个方面的技术问题：

a.初始温度选择。

退火初始温度T需能保证平稳分布中每个状态的概率趋于相等，如式(1)，本文选取初始温度为0.5 ℃。

exp[(F1-F2)/T]≈1

(1)

b.温度下降方法。

研究表明，退火温度下降方法的选取直接关系到计算量的大小和计算结果的准确性。本文选用线性下降方法，降温系数α=0.9，见式(2)。

Ti+1=αTi

(2)

c.算法终止条件。

模拟退火算法从初始温度开始，通过在每一温度的迭代和温度的下降，最后达到终止原则而停止。本文设定的终止温度为1×10-5℃，当退火温度达到终止温度时，认定扫描结束，此时的安全系数为全局最小安全系数。

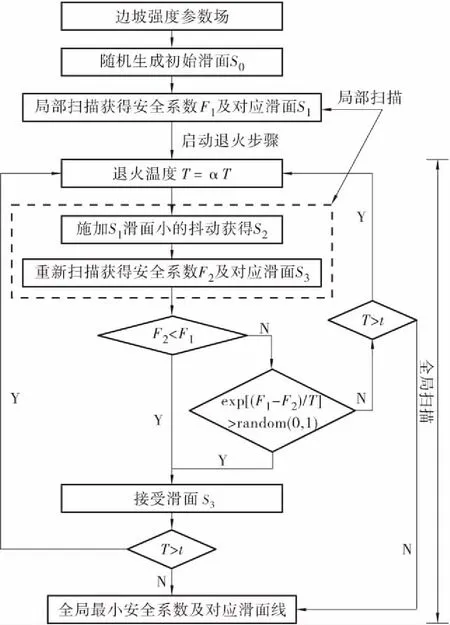
图3 模拟退火全局扫描计算流程图Figure 3 Global searching flowchart using SAA

3.2.2圆弧穷尽扫描算法

为对比说明，对穷尽扫描算法[7]进行移植，分析本文采用的三角网格边坡截面，搜索圆弧临界滑面，扫描示意见图4。

图4 三角网格圆弧扫描示意图Figure 4 Diagram of circular slip surface searching in triangular mesh slope section

图4中，截面上方的方格交点构成搜索滑面的圆心集，L1和L2线段分别表示扫掠圆弧最下端的上限和下限。将L1至L2之间的距离L进行n等分，对于每一个圆心O，则需要进行n次扫描，每次扫描的半径为：

(3)

式中:RL1为圆心到L1的垂直距离；i为针对某个圆心的第i次扫描。

提取图4中圆弧与网格线的交点，每相邻两交点之间的土条作为极限平衡法的一个计算单元。图4中ABCD就是一个计算单元，CD所在三角网格强度参数作为CD线上的强度参数。对每个圆弧滑面，采用朱大勇提出M-P简明算法进行安全系数求解计算[9]。

4 算例

4.1算例1

图5(a)为澳大利亚计算机应用协会(ACADS)发布的标准考题截面之一，截面尺寸、各层土体重度γ、粘聚力c及内摩擦角φ均在图中标示。首先采用本文所提出方法进行边坡的折线滑面稳定性分析，经试算可以确定当采用8节点7段线滑面时安全系数收敛，此时安全系数FsL=1.345。图5(b)中虚线为任意随机生成的8节点7段线初始滑面线。

(a) 边坡截面尺寸及物理参数

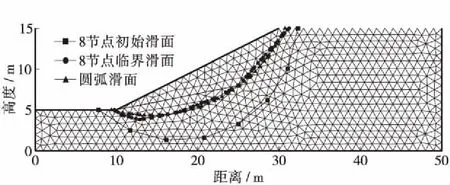
(b) 搜索得到的临界滑面图5 算例1参数Figure 5 The Parameters of exapnple 1

同时，对本文圆弧穷尽扫描算法分析本文采用的三角网格边坡截面，搜索圆弧临界滑面，计算所得安全系数Fso=1.370。GeoStudio 2007商业软件计算圆弧滑面安全系数Fsg=1.389。8节点临界滑面及圆弧滑面见图5(b)。图5(b)说明本文提出的截面网格划分方法具有良好的适应性，能够针对含不规则形状土层边坡进行稳定性分析。虽然本例中多段折线滑面与圆弧滑面很接近，但也很明显：多段折线滑面假设相对于圆弧滑面假设而言，能搜索得到更为危险的临界滑面，因而更具有使用优势。为清楚地显示，后续示意图不再画出三角网格。

4.2算例2

本算例为两土层中间夹杂一层软弱斜坡层边坡[11]，截面尺寸及物理强度参数见图6(a)。各滑面计算安全系数见表1，各方法得到的临界滑面见图6(b)。

(a) 边坡截面尺寸及物理参数

表1 各临界滑面计算安全系数Table1 FactorofSafetyforCriticalSlipSurfaces滑面类型安全系数4节点0.422多段折线滑面5节点0.4136节点0.4117节点0.410圆弧滑面本文0.425GeoStudio20070.425

结果表明多段折线滑面在折点数量n=6时安全系数达到收敛。图6(b)显示了随机生成的不同节点数量初始滑面扫描得到的临界滑面。多次试算显示，无论初始滑面位置如何，在给定节点数量的情况下，都可以搜寻得到相应的临界滑面，表明本文所提方法对初始滑面位置不敏感。只要生成初始滑面，就可以完全由程序自身完成临界滑面的全自动快速搜索。通过对比多段折线滑面和圆弧滑面，同样发现多段折线滑面展现出较圆弧滑面更为优异的搜索能力。

4.3算例3

图7(a)为文献[6]中未能直接进行全局极限滑面搜索的复杂土层边坡。在改良前，随机生成的初始滑面在经历多轮循环后极易落入局部极值，即图7(b)中的局部临界滑面S′，对应安全系数Fs′=1.82。因此，为完成此类复杂边坡的极限滑面搜索，需要通过引入工程师经验，预判滑面的可能位置，然后比较各可能位置计算之后的安全系数值大小，解算过程比较繁琐。

(a) 边坡截面尺寸及物理参数

(b) 搜索得到的临界滑面图7 算例3参数Figure 7 The Parameters of exapnple 3

引入模拟退火法之后，再次对这一复杂边坡进行了多次试算。为方便说明，图7(b)中的初始随机滑面选为①②③，分别代表初始滑面位置跨越不同土层区间。计算结果表明，只需要随机生成初始滑面的任意位置，而无论初始滑面落入哪个区间，本文算法总能得到收敛解，快速且自动搜索得到全局临界滑面S，对应安全系数Fs=1.55。

5 结论

本文采用Monte Carlo等角/等边逐段扫描与模脱空时梁段的挠度变化呈纵向分布，有脱空发生时梁段的挠度变化呈横向分布，无滑道脱空时梁段纵向两边的挠度基本为0，有些许下挠的趋势，中间梁段的挠度有向上翘起的趋势；滑道脱空后，从该滑道至临近区域段的梁体呈下挠趋势，其余梁体出现上翘现象。单滑道脱空时边滑道脱空引起梁体下挠较大，多滑道脱空中同侧边中滑道脱空引起梁体下挠明显大于其他脱空工况，达到6 mm以上。有限元分析结果表明：箱梁顶推时，支撑反力及梁体受力对滑道高程差非常敏感，毫米级的误差都将导致支撑反力发生剧烈变化，梁体局部有应力集中的风险，同时存在箱梁截面发生翘曲变形的可能。在实际顶推过程中，需对滑道高程偏差进行实时监控，通过动态调整保持各滑道横向始终处于同一高程，以减轻在顶推过程中由于滑道高程差导致的支撑反力差过大造成梁体局部受力集中的问题。

拟退火法相结合进行含软弱夹层边坡的多段折线全局临界滑面搜索。同时，编制了圆弧滑面穷尽扫描算法程序作为对比。以商业软件Fortran和Matlab为计算手段进行联合编程实现了Morgenstern-Price极限平衡搜索算法。计算结果表明：

a.截面三角网格划分方法具有良好的适应性，能较好地对不规则层位几何形状进行离散，进而方便后续计算分析。

b.多段折线滑面具有较圆弧滑面更为优秀的极限滑面定位功能，其安全系数随着滑面段数的增加会逐步达到收敛。

c.不再依赖于工程师经验进行初始滑面大致范围选择，避免了人为因素影响，本文所提算法能快速地、全自动地进行由弱到强不同复杂土质情况的边坡稳定性计算分析，并能找到全局临界滑面与安全系数。