以问题情境深化量感体验

龚莉 张国全

在立体图形体积的教学中，教师如何创设问题情境、设计学习任务，引导学生借助几何直观建立起长方体体积与长、宽、高或圆柱体积与底面直径、半径等的联系，通过操作、转化等构建立体图形体积的计算方法并解决相关实际问题，体验不规则物体体积的测量方法，区分体积与容积，从而强化学生的空间观念和量感呢？本期，我们讨论如何帮助学生更好地建构立体图形的体积。

《义务教育数学课程标准（2022年版）》对“体积”内容的核心要求是培养学生的量感，并指出“量感主要是指对事物的可测量属性及大小关系的直观感知”。教学中，教师如何创设问题情境，引导学生自主选择合适的方法对待测物进行量化，实现量感的进一步发展呢？笔者以人教版数学五年级下册第三单元“长方体体积的计算”教学为例，做具体阐述。

一、以问启疑，感知量感

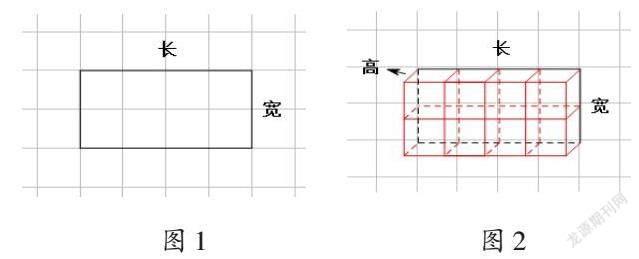
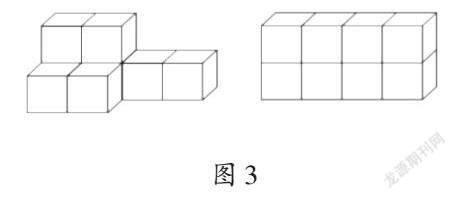
在前面的学习中，学生已经理解了长方形面积的本质即单位面积的累积。笔者将此作为引导学生理解长方体体积概念的基础，展示方格纸上的长方形（如图1），并提问：“在长方形所占的方格上，我们可以摆放什么图形将其占满？”学生认为可以密铺8个棱长为1cm的正方体（如图2）。

“这8个小正方体拼成了什么图形？怎样描述它的大小？”笔者引导学生分组交流。学生回答：“拼成了一个长方体，它的体积是8cm3。”笔者让学生描述得具体一些。学生回答：“拼成了一个长4cm、宽2cm、高1cm的长方体。”笔者追问：“你如何确定其体积是8cm3？”学生回答：“因为它有8个单位体积，所以它的体积是8cm3。”

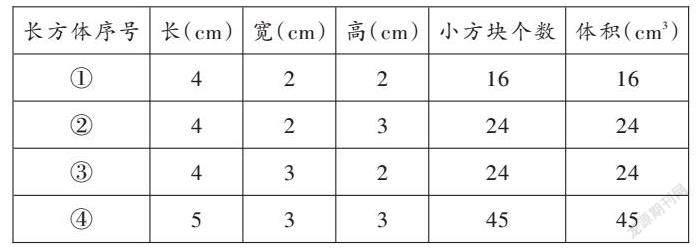
接着，笔者将此长方体先后拆分，重組为以下两个图形（如图3）。

笔者要求学生观察重组图形，通过解决“这两个重组图形的体积是多少？”“还可以怎样摆放？”“重新摆放后其体积是否有变化？”等问题，从不同视角感知体积的可测量性，进而使学生意识到图形的大小与形状无关，单位体积的累积才是关键。

二、以问促思，建构量感

在“建构量感”环节，笔者让学生在原有长方体的基础上添加更多的小正方体，拼出不同的长方体，并在统计表中记录相关数据。这样做的目的是引导学生借鉴探索长方形面积的方法进一步探索长方体的体积，并感知要选择合适的度量单位测量长方体的大小。

学生同桌交流并用1cm3的小正方体学具实际拼摆后汇报：“可以在原有的长方体上再密铺一层小正方体，这样就得到一个长4cm、宽2cm、高2cm的长方体”，“也可以再铺2层，这样就得到一个长4cm、宽2cm、高3cm的长方体”。学生受课始活动的影响，只想到了改变长方体的高。笔者追问：“你们还有不一样的想法吗？”一名学生提出：“继续往上铺，可以拼成无数个新的长方体。”笔者提示：“只有改变高才能产生新的长方体吗？还有没有别的方法呢？”学生疑惑：“可不可以往左或往右再多铺几列呢？”笔者及时给予肯定，学生的思路逐渐打开：还可以往后再铺一排、两排……笔者通过不断地追问，使学生不再拘泥于改变原有长方体的高的固定思维，并在操作过程中发现改变长、宽、高都会改变长方体的大小。

笔者选择了几组有代表性的数据记录下来（如下表），并让学生分组讨论，分析表中的数据。

汇报时，学生代表甲说：“单位体积的个数和长方体体积的数值相同。例如，长方体①是由16个1cm3的小正方体摆成，长方形①的体积就是16cm3。我们通过数小正方体的个数就可以知道长方体的体积。”一名学生提出疑问：“如果是一个很大的长方体，而我们没有那么多小方块怎么办？”另一名学生回答：“可以用更大的体积单位来数，如1dm3、1m3等。”学生代表乙说：“长方体②与长方体③的体积大小相同。这让我们想到之前局部拆分、重组的两个图形（如图3），于是我们把两个长方体都摆了出来，发现把长4cm、宽2cm、高3cm的长方体以长为轴旋转90°，就能得到长4cm、宽3cm、高2cm的长方体。”小组成员补充道：“还可以以宽为轴，将长方体立起来，就得到了长3cm、宽2cm、高4cm的长方体。”小组成员在投影仪上展示他们描述的三种拼摆长方体的方式，让其他学生看到长、宽、高相互转化，体积的大小不变。学生代表丙说：“与原长方体相比，长方体④在长、宽、高上都有所增加，它的体积也是几个长方体中变化最大的。”其他学生反驳：“那是因为添加的小正方体的数量少，如果把长方体①增加的部分变大，变成长4cm、宽2cm、高10cm的长方体，即摆10层，其体积就比长方体④大了。”小组成员补充道：“我们还可以同时增加长、宽、高，使其成为体积变化最大的长方体。”

教师通过创设问题情境，让学生在操作活动中直观感知长方体的大小关系，客观地理解长方体各元素的变化给体积带来的变化，为学生提炼长方体的体积公式及后期的变式应用打下了坚实的基础。

三、以问研学，深化量感

本环节，笔者提出了三个问题，引导学生在实践操作中加深量感体验，深入研究长方体的体积公式：①从表格中选择一个图形，实际摆一摆，仔细思考如何让操作过程更简洁；②思考用什么方法确定长方体的个数；③所摆长方体中每行小正方体的个数、摆的行数和层数与长方体的长、宽、高有什么关联。

第一小组边操作边讲解：“我们用1cm3的小正方体摆长方体①，沿着长密铺4个，沿着宽密铺2个，沿着高密铺2个，即每行摆4个，摆2行，铺2层。根据乘法的意义，4×2×2=16，说明这个长方体包含了16个小正方体，它的体积是16cm3。”学生在操作中理清了“每行的个数”“行数”“层数”与长方体长、宽、高的对应关系，为建立体积公式提供了经验。第二小组边操作边讲解：“我们先摆长方体①，用8个小方块把底面铺满，再沿着高铺2个小方块，即底面铺8个，铺了2层。长方体①的体积为：8×2=16cm3。”这种方法阐述了“底面的个数”与“长方体的底面积”的对应关系。问题情境的层次性与操作性使学生在思辨中深化了对“长方体体积=长×宽×高=底面积×高”的理解。

（作者单位：龚莉，枣阳经济开发区靳庄小学；张国全，枣阳经济开发区中心学校）

责任编辑  张敏