内波与地形作用过程研究

王春凌 王寅

摘要：内波是分层水体中普遍存在的水动力现象，破碎产生的湍流是打破水体层化的重要机制之一。本文采用数值模拟技术模拟研究了内孤立波与典型大陆坡的相互作用过程。

关键词：破碎；内孤立波；能量耗散；地形

基金项目：国家自然科学基金青年基金项目

项目编号：52009087、52109090

基金项目：浙江省自然科学基金公益项目

项目编号：LGF19E090005

基金项目：中国博士后科学基金面上项目

项目编号：2022M721426

一、研究背景

内波是密度层化水体中内界面波动现象，在遭遇地形或障碍物时，内波会发生不同程度的破碎，激发的紊流有助于局部水体混合，改善局部水质，无规律的水质点运动作用于结构，使结构体发生“涡振”，破坏结构稳定性。内波破碎和诱发机制复杂，Saffarinia和Kao等人用数值方法模拟了两层流体中内孤立波在平坦地形上传播和破碎，发现当波面指点流速超过内波相速度时，下层水体被卷跃至上层，内波发生破碎且此时波幅为上层水深的2.65倍，指出波的破碎是对流不稳定导致的。Vlasenko和Hutter对内孤立波与大陆架作用过程模拟发现，浅水效应使内波波面不断陡峭直至翻转、破碎，此时的破碎由对流不稳定引起，随后Afansyev和Peltier、Legg和Adcroft、Klymak和Pinkel等也得到类似结论。Barad 和Fringer等人的研究则指出，剪切不稳定同样可导致内波发生破碎，在内重力波和加速剪切流的传播过程中，剪切不稳定的发生取决于剪切流的加速度，即当加速度较小时，内波会因为剪切不稳定发生破碎，且内波诱发紊流产生的水体混合效率与不稳定剪切相关。然而，自然条件下内波破碎通常是对流不稳定和剪切不稳定共同作用的结果，不稳定特征与波幅和传播方向相关。刘国涛等人对内波在白噪声干扰下引起的不稳定现象进行分析，结果显示，静力不稳定最先出现，持续时间较长，随后剪切不稳定和对流不稳定相继出现。

关于内波破碎判据，Helfrich将离岸最远的初始湍流斑点出现位置定义为内波破碎位置，并得出当a/d≥0.4±0.1（a是斜坡起点处波幅，d是破碎位置的下层水深）时，内波发生破碎。Vlasenko和Hutter认为：当无量纲振幅a*=am /（Hb－Hm）满足a*=0.8/γ+0.4时，如果Hs＜Hb，内波的背风面在斜坡上破碎，反之会以频散尾波的形式继续传播。Fringer和Street认为内波破碎发生的不稳定主要与界面厚度相关，并给出kδ＜0.56时（k为水平波数，δ为界面厚度），内波波峰和波谷出现Kelvin－Helmholtz（K－H）不稳定；当0.56≤kδ＜2.33时，初始不稳定为剪切不稳定；当kδ≥2.33时，由于界面厚度较大无法形成K－H不稳定，为对流不稳定。Troy的研究结论认为当0＜kδ＜0.66时，扰动长度仅随界面厚度变化，具有最大增长率的扰动得以充分发展，形成K－H滚动，内波破碎主要是剪切不稳定引起；当0.66≤kδ＜0.3时，扰动增长率减小，剪切不稳定不能充分发展；当kδ≥1.3时，剪切不稳定不可能发生，内波不发生破碎。

Barad和Fringer分别给出不稳定性的判据条件：Richardson数Ri小于0.1；σT＞5， T是Ri数＜0.25的时间长度，σ是扰动在此时间内的平均增长率；Lw/L＞0.86， Lw是Ri＜1/4区域的长度的一半，L是内波的半宽度。近年来，有研究者提出内波破碎与地形坡度和内波坡度的比值相关，比值越小，破碎掺混越剧烈。相对于斜坡，孤岛地形导致的内波破碎通常用阻塞系数ζ（ζ=（a+H1）/（H1+H2+hs），a是波幅，H1、H2分别为上下层水深，Hs是障碍物高度描述将内波与障碍物作用程度分为弱作用（ζ＜0.55），适度作用（0.55＜ζ＜0.7）和内波破碎（ζ＞0.7），各研究者根据阻塞系数的取法不一致，结论有所不同。对于三层分层流体中的第二模态内波，当阻塞系数0.2＜B＜2（B=am/?h， am为波幅，?h为内界面到地形顶面的高度）时，内波将完全破碎分解。

针对内波能量计算，多数研究者的论文中采用下式估算内波势能：

； （1）

此法简单易行，只需勾勒出波面形态即可进行估算，多用于物理水槽试验中。然而，在内波破碎剧烈情况下，用此方法进行势能估算误差较大，一方面，混合区界面无法准确捕捉；另一方面，作用过程形成的小尺度和微尺度内波难以被精确刻画。

综上所述，内波破碎仍有两个问题有待进一步探讨：内波破碎过程特征尚未确定；传统内波势能计算公式存在一定局限，真实能量的损耗、转化需进一步分析。

本文通过数值模拟方法，系统研究典型地形与内波作用过程，分析水体剪切不稳定和对流不稳定发生机制，确定内波与大陆架地形破碎的基本特征。同时，为探求更为精确的内波能量损失值，对用式（1）的估算值进行分析和修正，为理论模型用于实际工程提供可靠的参考及修正依据。

二、数学模型

（一）控制方程

基于连续介质假设，描述不可压缩粘性流体的连续方程和动量方程为：

； （2）

；  （3）

式中，ui 和xi分别是i方向的速度和坐标；ρ是压强；是流体密度，本研究中清水密度取值1000kg/m3，盐水密度取值为1030kg/m3；t是时间；μ是流体动力黏度；gi是i方向加速度，竖直方向取值为－9.8m/s2，其他方向取值为0；si是动量源项。

通常将内波概化为两层分层流体的多相流问题，数值计算中通过求解体积分数对当地物理量进行更新：

且   ； （4）

式中，λ为更新的物性值，例如密度，Φm和λm分别为第m相的体积分数和相属性值。对于不可压缩两相流，只需计算某一相体积分数，余下即为另外一相。

本文采用大涡模型求解控制方程，滤波后的控制方程和体积分数输运方程为：

（5）

τij为亚格子应力项，是可解尺度运动与亚格子尺度运动之间的动量输运，需进行模化处理，采用拟序涡结构模型封闭方程。

（二）求解方法和边界条件

采用结构化网格对计算区域进行离散，通过分步法（Fractional Method）分别求解对流项、扩散项和压力项，方程如下：

； （6）

； （7）

； （8）

式中，“*”和“**”分别代表对流步和扩散步求解的中间物理量，“n”代表当前时刻，“n+1”代表新时刻。在得到流场后，求解体积分数（Volume Of Fraction，简称“VOF”）输运方程：

； （9）

同时，由式（3）更新本地密度。

边界是否设置合理直接关系计算收敛和数值准确性。本文中水槽自由液面采用垂向速度为零，其他方向速度梯度为零；底部采用固体壁面边界；入流边界采用滑移边界；出流采用Sommerfeld边界，避免入射波反射。

应用两层流体内波关系式：（h1+a） U1 = （h2-a） U2 = c0η， 得到上下层水体的理论流速值。其中，η为波面高; h1和h2分别为上下层水深；U1和U2分别为上下层理论平均流速。基于波面函数和流速理论解，采用边界造波方法进行数值造波，与传统方法相比，该方法保证了完整的波形，便于波能计算。

三、模型实验及结果

（一）模拟试验

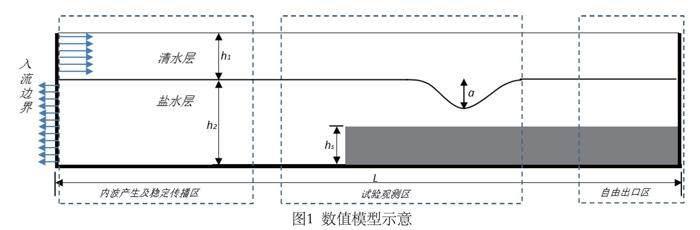
试验在一数值水槽中进行，水槽长10m、宽0.5m、高0.4m，图1为数值水槽示意图。在入流边界定义流速进行造波，速度如何取值见上文。hs为大陆架高度，h1和h2分别为清水层和盐水层厚度，清水密度为1000kg/m3，盐水密度为1030kg/m3，水槽右侧为自由开边界，防止反射波影响试验观测区。

（二）模拟结果

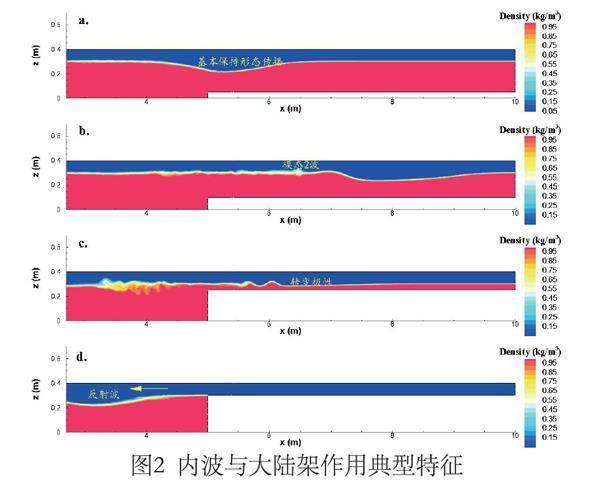
模拟实验揭示了下凹型内孤立波与大陆架地形相互作用过程，该过程可分为三种情况：当地形高度与内分界面距离较大时，内孤立波不受影响继续保持原有波形前行（图2a）。随着地形高度增加，在内孤立波接近地形过程中，由于局部水流增大波面发生不同程度的扭曲变形甚至破碎产生紊流。因此，内孤立波也被称为水体的天然搅拌器。局部的混合不仅利于上下层水体打破分层将富含氧的水体输送到底层，其形成的第二模态内波（图2b）还可实现界面处的物质远距离输运。除此之外，模拟研究发现与地形作用过程中存在内孤立波转变极性的情况（图2c），这主要取决于地形上方的上下层水深比。根据KdV理论，h1/h2的值偏离1，其非线性越明显，表现在波形上是波幅越大；反之，表现为弥散作用占主导，即波形越变得扁平。

当地形高度等于或高于分层界面时，内孤立波几乎完全反射（图2d），但反射系数与大陆架坡度有一定相关性，这一点在Chen等人（2007）的研究中已得到证实。图3中为直角大陆架和非直角大陆架上内孤立波诱发的流场，图中内孤立波向右传播，引起的下层水体流向与波的传播方向相反，很明显在直角大陆架的迎波面有逆时针的漩涡形成，原因是直角处的水体受剪切；当坡面较缓更贴合水流特性，坡底水体受剪切不易形成漩涡。漩涡的存在大大增加了对底部的剪切，造成地形不同程度的侵蚀，消耗的能量也相对较多。图4为直角大陆架和非直角大陆架对内波能量消耗的对比图，从图中可以看出，直角大陆架消耗的内波能量高于带坡度大陆架地形约1.5%，整体能量损失随地形高度先增后减且符合线性规律，峰值位置出现在km≈0.3处，大小约为初始能量的20%～25%。

四、结语

本文采用数值试验的方法对内波与典型大陆架地形的相互作用过程进行了模拟，通过分析流场和能量计算得到如下结论：

内波与大陆架作用的演变过程与地形高度相关，当地形高度小于下层水深1/6时，内波几乎不受地形影响保持原有形态前行；当高度超过此数值，内波的演变还与地形上的上下层水深比相关，根据该比值偏离1的程度发生裂变和转变极性。同时，伴随内波第二模态出现，地形上方水深比大于1时，第二模态波跟随反射波；反之，模态二波跟随透射波。

与地形作用过程损失的能量与地形高度相关，随地形高度的增加出现先增后减的趋势，且在无量纲参数km=0.3时，耗散能量达到峰值，约占初始能量的20%～25%。

与非直角大陆架相比，直角大陆架消耗的能量偏多，主要原因是与地形作用过程中在坡脚产生旋涡结构，该结构加大了水体剪切，从而加速能量损耗。

参考文献：

[1]Aghsaee，P.and L.Boegman.Experimental Investigation of Sediment Resuspension Beneath Internal Solitary Waves of Depression.Journal of Geophysical Research：Oceans，2015，

120（05）： 3301-3314.

[2]Zhu，H.，L.Wang，and H.Tang. Large-eddy Simulation of the Generation and Propagation of Internal Solitary Waves.Science China Physics，Mechanics & Astronomy，2014，57（06）：1128-1136.

[3]Saffarinia，K.and T.W.Kao，A Numerical Study of the Breaking of an Internal Soliton and Its Interaction with a Slope.Dynamics of Atmospheres and Oceans，1996，

23：379-391.

[4]Vlasenko，V.and K.Hutter.Numerical Experiments on the Breaking of Solitary Internal Waves. Journal of Physical Oceanography，2002，32：1779-1793.

[5]Vlasenko，V.I.and K.Hutter.Generation of Second Mode Solitary Waves by the Interaction of a First Mode Soliton with a Sill.Nonlinear Processes in Geophysi-cs，2001，08（4/5）：223-239.

[6]Barad，M.F.and O.B.Fringer.Simulations of Shear Instabilities in Interfacial Gravity Waves. Journal of Fluid Mechanics，2010.644：61-95.

[7]刘国涛，尚晓东.海洋内波能量耗散的数值研究[J].海洋石油，2019，39（01）：82-87.

[8]Helfrich，K.R.Internal Solitary Wave Breaking and Run-up on a Uniform Slope. Journal of Fluid Mechanics，1992，243：133-154.

[9]Arthur，R.S.and O.B.Fringer.The Dynamics of Breaking Internal Solitary Waves on Slopes. Journal of Fluid Mechanics，2014，761：360-398.

[10]Maderich，V，et al.Numerical Simulations of the Nonhydrostatic Transformation of Basin-Scale Internal Gravity Waves and Wave-Enhanced Meromixis in Lakes， in Nonlinear Internal Waves in Lakes，2012：193-276.

[11]Talipova，T，et al.Internal Solitary Wave Transformation Over a Bottom Step： Loss of Energy. Physics of Fluids，2013，25（03）：032110.

[12]Liu，A.K，et al.Generation and Evolution of Mode-two Internal Waves in the South China Sea.Continental Shelf Research，2013（59）：18-27.

[13]Chen，C.Y.Amplitude Decay and Energy Dissipation Due to the Interaction of Internal Solitary Waves with a Triangular Obstacle in a Two-layer Fluid System：the Blockage Parameter.Journal of Marine Science and Technology，2009，14（04）：499-512.

[14]Wang，C.，etal.Numerical Modeling of Energy Dissipation of Internal Solitary Waves Encountering Step Topography.Ocean Engineering，2022，259：111853.

[15]Wang，C.L.，L.L.Wang，andH.W.Tang，Depression Internal Solitary Wave Interaction with Submerged Obstacle.Journal of Environmental Biology，2016，37（05）：1217-1223.

[16]Chen，Y.C.，et al.Wave Propagation at the Interface of a Two-layer Fluid System in the Laboratary.Journal of Marine Science and Technology，2007，15（01）：8-16.

作者简介：王春凌（1985），男，安徽省安庆市人，中级讲师，博士学历，主要研究方向为水力学。