从“苦学”到“乐学”，悟思维之灵动

彭晓梅

著名数学家华罗庚也说过：“就数学本身来说，也是千姿百态，壮丽多彩，引人入胜的。”数学为什么“好玩”？数学凭什么“引人入胜”？因为数学美啊！

数学美在对称，美在简洁，美在严谨，美在秩序，美在规律，更美在思维之灵动，对于同一个题目能从不同的角度用多种解题方法和思路解答。今天我结合一个实例通过活跃的思维来体会数学之美。

在学习了角的基本知识之后，学生们对钟表的时针和分针所形成的夹角的度数问题产生了极大的兴趣，但是在求解的过程中却遇到了一些困难，根据学生们思考角度的不同，我把时针与分针的夹角问题总结出多种解题方法。

一、基本知识铺垫

普通钟表相当于圆，其时针或分针走一圈均相当于走过360°角，360度角被分成12格，一格对应的角度为30°，这一格分针需要用五分钟走过，时针需要用一小时即60分钟走过，时针的一小时或分针的 5 分钟因而时针每走过1分钟对应的角度为0.5°，分针每走过1分钟对应的角度应为6°。

二、计算举例（此类题目需要注意，我们要求的夹角问题默指小于180°）

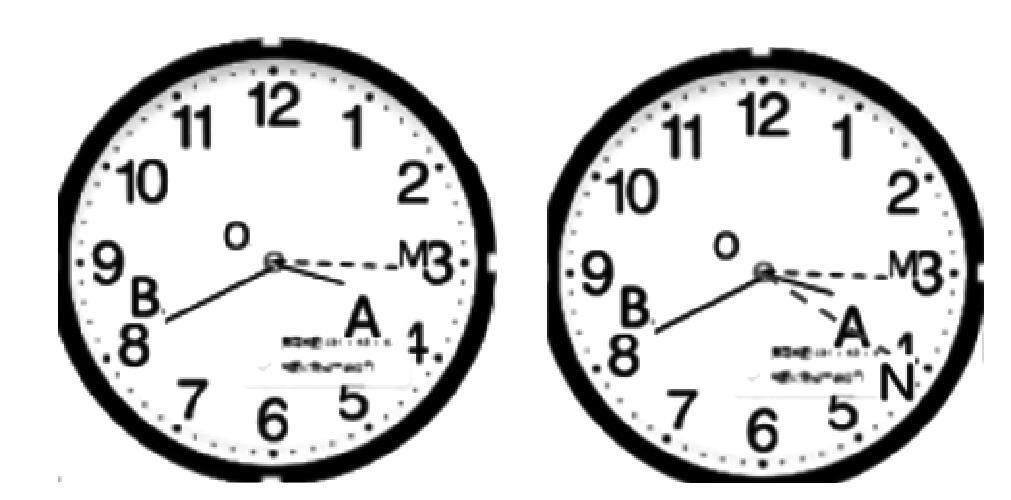
例：钟表上时间为 3：40 时，计算时针与分针夹角的度数

（一）解法一：利用角的和差关系

此题中我们要求的角度为图中的∠AOB

∠AOB=∠MOB-∠MOA

∠MOB=30°×5=150°

∠MOA=0.5°×40=20°

所以∠AOB=∠MOB-∠MOA=150°-20°=130°

或者∠AOB=∠NOB+∠NOA

∠NOB=30°×4=120°

∠NOA=30°-∠MOA=30°-20°=10°

所以∠AOB=∠NOB+∠NOA=120°+10°=130°

（二）解法二：可以把这个问题看成行程问题，求路程差（默认时针和分针的原始位置都是从指向12也就是0时0分开始）

解析 ：依据常识，我们应该以时针、分针均在12点时为起始点进行计算由于分针在时针前面，我们可以先算出分针走过的角度，再减去时针走过的角度，即可求出时针与分针夹角的度数。

1.先看分针：从原始位置0时0分到3时40分，共转过40分钟，所以分针走过的路程为40×6°=240°。

2.再看时针：从原始位置0时0分到3时40分，共转过3小时40分钟，即220分钟，所以时针走过的路程为220×0.5°=110°。

3.此时分针走过的路程比时针多，所以夹角为240°-110°=130°。

注：路程差即为路程的差的绝对值（在某些时刻时针走过的路程比分针走过的路程多）。

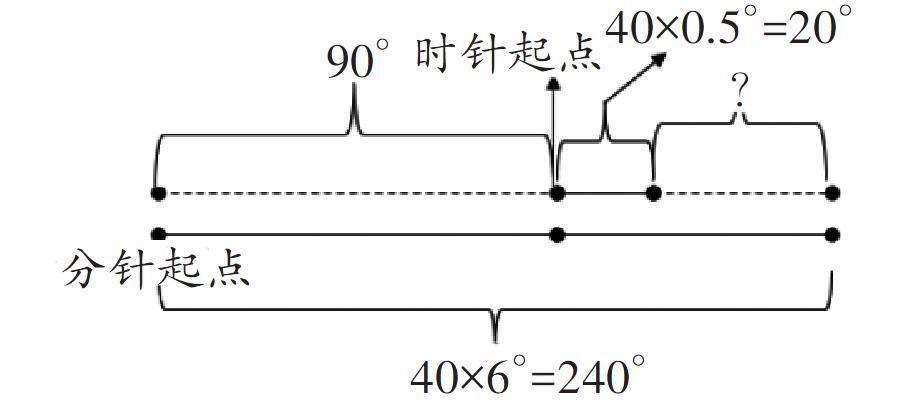
（三）解法三：可以把此问题看成追及问题

解析：我们可以把时针和分针回归到整点，3：40即回到3：00，从3：00到3：40，分针和时针都在跑，最终分针超过了时针。我们可以用线段图来表示：[40×6°=240°][分针起点][90°][40×0.5°=20°][时针起点][？]

由线段图不难看出，我们要求的角度=240°-90°-20°=130°。

三、总结

以上三种方法各有自身的优点，结合教学经验，可以把它们的优缺点总结如下。

解法一把所求角度转化成线段和差问题非常的直观，但是不同的时刻图形不一样，需要每个题目分别对应分析。

解法二可以总结出一个求夹角的公式，例如x时y分所成的夹角即为：

|0.5（60x+y）-6x|=|30x-5.5y|，这个公式可以不用看图直接套用求角度。

解法三把钟表问题看成一个行程问题，也就是类似于我们之前学过的操场上跑步的问题，这个可以与一元一次方程结合起来，让学生的思维更开阔，更灵活，这种方法更适合于求时间差的问题，例如“某人下午6点到7点外出购物，出发和回来时发现表上的时针和分针的夹角都是110°，此人外出购物用了多少分钟”，在追及问题中我们都知道时间差=路程差÷速度差，所以此题结果为220÷5.5=40分钟。

上述问题只是众多数学课堂中的一小节，当上述解题思路在数学课堂中得以展现的时刻，可以想象到学生们在课堂上思维碰撞的激烈和收获的喜悦，当学生的思维活跃起来，就像足球场上奔跑的运动员，他们感受不到挥汗如雨的劳累，只能感受到收获后心中满满的美。

在数学教学中，要充分挖掘数学美的因素，引导学生逐步体验到数学美，从直觉到知觉，从知觉到感悟，使他们走入“乐学”的天地。