巧算时针与分针夹角的度数

✿ 哈尔滨市第69 中学 王虹

在初中数学教学中，钟表问题经常出现，学生计算起来也比较困难，尤其在计算时针与分针夹角度数的问题上，因其计算方法很多，一直困扰着很多教师.本文结合自己教学过程中的体会，总结出使这类计算问题更便捷的规律和方法，供各位同行参考.

一、知识预备

（1）普通钟表相当于圆，其时针或分针走一圈均相当于走过360°角；

（2）钟表上的每一个大格（时针的一小时或分针的5分钟）对应的角度是

二、计算举例

例1：如下图1所示，当时间为7点55分时，计算时针与分针夹角的度数（不考虑大于180°的角）.

解析：依据常识，我们应该以时针、分针均在12点时为起始点进行计算.由于分针在时针前面，我们可以先算出分针走过的角度，再减去时针走过的角度，即可求出时针与分针夹角的度数.

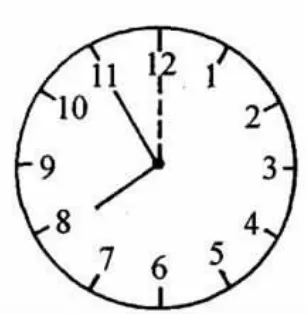
图1

分针走过的角度为：

55×6°=330°.

时针走过的角度为：

7×30°+55×0.5°=237.5°.

则时针与分针夹角的度数为：

330°-237.5°=92.5°.

例2：如下图2所示，当时间为7点15分时，计算时针与分针夹角的度数（不考虑大于180°的角）.

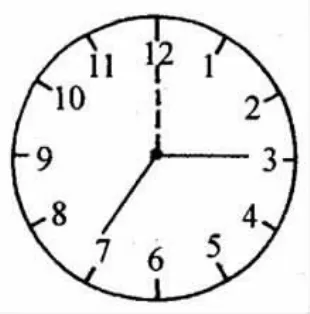
图2

解析：此题中分针在时针的后面，与上题有所不同，我们应该先算出时针走过的角度，再减去分针走过的角度，即可求出时针与分针夹角的度数.

时针走过的角度为：

7×30°+15×0.5°=217.5°.

分针走过的角度为：

15×6°=90°.

则时针与分针夹角的度数为：

217.5°-90°=127.5°.

三、总结规律

从上述两例我们可以总结出如下规律：当分针在时针前面，可以先算出分针走过的角度，再减去时针走过的角度，即可求出时针与分针夹角的度数；当分针在时针后面，可以先算出时针走过的角度，再减去分针走过的角度，即可求出时针与分针夹角的度数.

用字母和公式表示：

当时间为m点n分时，其时针与分针夹角的度数为：

（1）分针在时针前面：

n×6°-（m×30°+n×0.5°）.

（2）分针在时针后面：

（m×30°+n×0.5°）-n×6°.

依据此公式可以求出任意时刻时针与分针夹角的度数，计算起来非常便捷.如果题目中涉及到秒，可以让学生先把秒换算为分，再套用上述规律和公式进行计算即可.