GPS频间钟差特性分析及其对三频PPP的影响

张 蒲，屈利忠，王鲁平，王昊俣

GPS频间钟差特性分析及其对三频PPP的影响

张 蒲，屈利忠，王鲁平，王昊俣

（北京建筑大学，北京 102616）

针对全球定位系统（GPS）频间钟差（IFCB）显著影响多频精密单点定位（PPP）性能的问题，对全部GPS在轨的三频卫星的IFCB变化特性进行分析：可知Block IIF卫星IFCB单日内变化从厘米到分米不等，存在明显的时变特性，而Block III卫星单日内变化量级较小，通常不超过1 cm，IFCB的时变特性相比于Block IIF卫星得到了明显的削弱；同时，Block IIF卫星的IFCB存在12、6、8、4、4.8和3 h的周期变化，并以此建立IFCB高阶谐波模型。实验结果表明，对于静态PPP，利用IFCB预报值改正后，定位精度在东（E）、北（N）、天（U）3个方向上分别提升29.4%、39.4%、35%；而对于动态PPP，利用IFCB预报值改正后，定位精度在E、N、U3个方向上分别提升34.3%、20.0%、47.7%，同时可有效消除载波相位验后残差中的系统误差。

全球定位系统（GPS）；频间钟差（IFCB）；特性分析；建模与预报；精密单点定位（PPP）

0 引言

近些年来，随着美国全球定位系统（global positioning system，GPS）的现代化，俄罗斯格洛纳斯系统（global navigation satellite system，GLONASS）的复兴，我国北斗卫星导航系统（BeiDou navigation satellite system, BDS）、欧洲伽利略卫星导航系统（Galileo navigation satellite system, Galileo）相继部署完成，全球卫星导航系统（global navigation satellite system，GNSS）已经迈入新的发展阶段[1]。新一代的GNSS均能播发3个或更多频率信号，多频信号的可用性为精密单点定位（precise point positioning，PPP）模糊度快速解算[2]、完整性监测[3]、电离层延迟改正[4]等诸多领域的应用带来了新的发展机遇。然而，多频信号的引入带来诸多优势的同时，随之易产生一系列与频率相关的偏差，需要谨慎考虑。文献[5-6]研究发现，GPS Block IIF-1卫星L1/L2与L1/L5卫星钟差之间存在与卫星热效应有关的周期性变化，振幅可达分米级，通常把这项偏差定义为频间钟差（inter-frequency clock bias，IFCB）。IFCB的存在会对多频PPP的定位性能造成显著影响。目前各分析中心发布的GPS精密钟差产品是传统的L1/L2无电离层组合钟差，为了将L5信号引入到多频PPP中，国内外学从IFCB的估计方法、建模与预报以及对三频PPP的影响等方面展开了相关研究。

目前IFCB估计方法主要有3种，即最小二乘法[6]、历元间差分法[7-8]以及非差非组合网解法[9]。最小二乘法和历元间差分法均利用三频载波相位无几何无电离层组合（geometry-free and ionospheric-free, GFIF）估计IFCB，最小二乘法由于涉及GFIF组合模糊度参数的估计，算法较为复杂且计算效率相对较低，而历元间差分法消除了GFIF组合中的模糊度参数，通过实验表明该方法数据处理效率约为最小二乘估计方法的1.5倍，实现了IFCB的高效估计[7]。非差非组合网解算法直接估计L5频率的卫星钟差，再转换为IFCB，但该算法待估参数较多，导致计算效率远不如历元间差分算法。文献[6]建立了与时间和太阳、卫星、地球之间角度相关的四阶经验改正模型，建模精度1 cm。文献[7]等采用傅里叶变换发现IFCB时间序列中存在12、8、6 h的显著周期性变化，建立的四阶谐波模型对于伪随机噪声识别码（pseudo random noise code, PRN）01卫星和 PRN25卫星的校正率分别为77.1%和77.9%，但未进行相应的PPP验证。文献[10]在此基础上建立了6阶谐波模型建模精度4 mm，采用该模型24 h预报精度7.2 mm，利用预报值进行预先改正，三频PPP定位精度在东（E）、北（N）、天（U）3个方向分别提升21%、11%和16%。

随着多频信号的发展趋势以及市场对于实时高精度定位需求的日益增加，IFCB的高效估计、精确建模和预报，对于一致使用现有钟差产品进行实时多频高精度数据处理具有重要意义。鉴于此，本文推导顾及IFCB的GPS三频非差非组合PPP函数模型，并给出IFCB估计方法。同时，对全部GPS三频卫星IFCB变化特性进行分析，根据IFCB变化特性构建IFCB预报模型，并通过定位验证结果分析IFCB预报值对于三频静态、动态PPP的影响。

1 顾及IFCB的GPS三频PPP模型

GPS非差原始伪距和载波相位观测方程可以表示为

为了与当前发布的精密钟差产品保持兼容，将卫星端的伪距硬件延迟和载波相位硬件延迟中的时变部分纳入到卫星钟差的估计中，接收机端的伪距硬件延迟则与接收机钟差共同估计[10]，可表示为

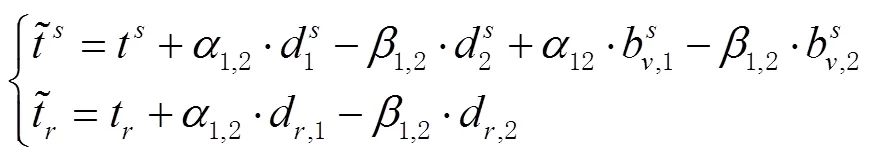
2 IFCB估计与建模方法

2.1 IFCB估计

基于三频载波相位GFIF组合的IFCB估计方法[8]可表示为

2.2 IFCB预报模型

考虑到IFCB时间序列中呈现出显著的周期变化，基于周期特性的谐波模型可表示为：

可利用快速傅里叶变换确定IFCB时间序列中较为显著的周期变化，而周期项选取的准确性是该建模方法的关键。为了便于估计式（8）中的初始相位，通常将模型线性化为

式（9）中各参数的转换关系为

3 实验与结果分析

3.1 数据来源

从全球均匀分布的116个多模GNSS实验跟踪网（multi-GNSS experiment，MGEX）跟踪站收集观测值数据，所选站点均具备GPS L1、L2、L5三频信号的跟踪能力，站点在全球范围内的地理分布情况如图1所示。

图1 所选MGEX跟踪站分布

图中：用圆点表示的100个跟踪站作为基准站，观测值数据用于IFCB估计；用五角星表示的16个跟踪站作为流动站，用于静态、动态三频PPP定位验证。这些MGEX站的观测数据均包含全部GPS三频卫星，包括12颗Block IIF卫星以及4颗Block III卫星。数据起止时间为2021-05-01—2021-05-30（年积日第121—150天），数据时长为30 d，采样间隔为30 s。为了保证观测值数据质量，将卫星高度截止角设置为7°。

3.2 IFCB变化特性分析

利用基于GFIF组合的历元间差分算法对IFCB进行估计，其中选择 GPS 时间00:00:00历元作为参考历元，并每天将其设置为0。2021-05-01—2021-05-03的IFCB估计结果如图2所示。受限于篇幅，Block IIF卫星以G01、G06为例，Block III卫星以G14、G23为例。

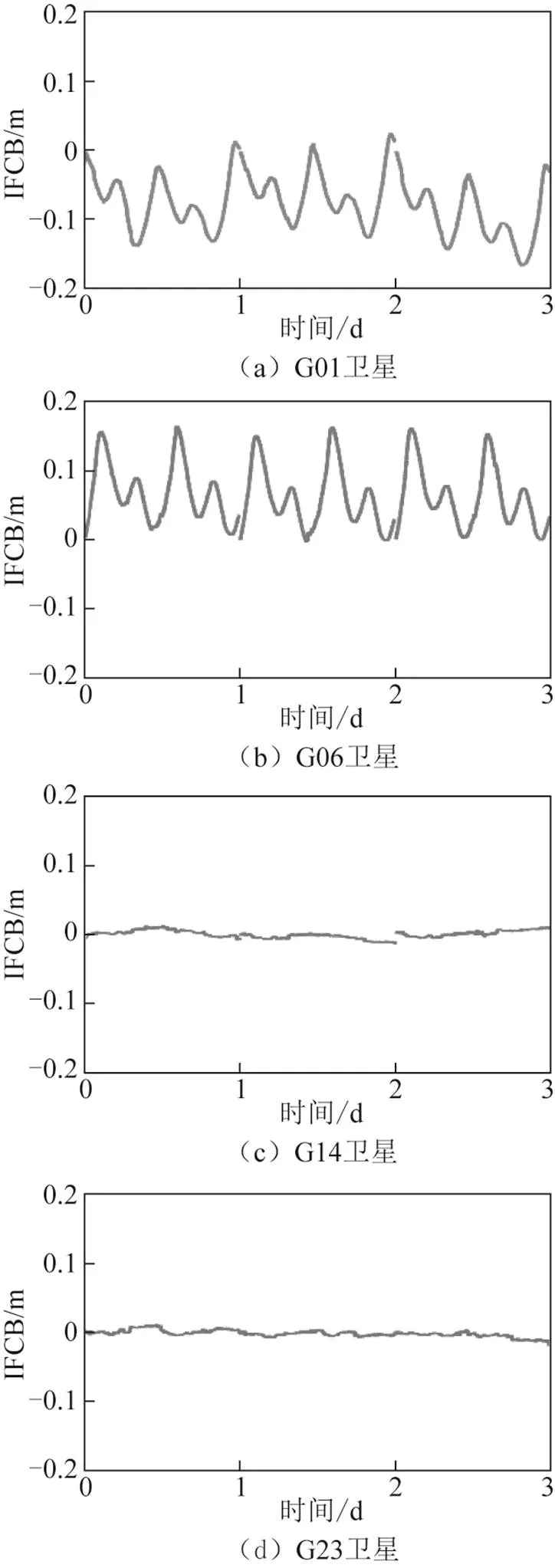
图2 IFCB时间序列

从图中可以看出，GPS卫星IFCB随时间变化而变化，但不同类型卫星变化范围并不一致。其中Block IIF卫星IFCB的变化量从厘米到分米不等，如G06卫星，峰值振幅最大可接近20 cm。相比之下，Block III卫星IFCB量级较小，通常峰值振幅低于1 cm。表1列出了单日IFCB的均方根（root mean square，RMS）统计量。

从表中可知：Block IIF卫星的RMS均大于0.02 m，其中G01和G24的RMS统计量最大，可达到0.086 m；Block III卫星的RMS均不超过0.011 m，除了G18卫星外，其他卫星RMS统计量均低于0.01 m；此外，Block IIF卫星在时域上呈现出明显的周期性变化，天与天之间变化趋势相似，而Block III卫星周期性变化并不显著。

表1 单日IFCB的RMS统计表 m

为了进一步探究IFCB的变化特性，对30 d的IFCB时间序列进行小波分解。对于小波函数的选取，由于Sym5小波[13]为连续小波，且相较于其他小波函数具有更好的对称性，能减少对信号分解时的相位失真，因此本文选取Sym5小波对IFCB进行7级分解。分解后的高频分量包含了相位多路径和测量噪声，而低频分量反映长期变化，即反映了IFCB的时变特性。图3给出了高频分量和低频分量的RMS统计值。

图3 IFCB高频分量和低频分量统计

从图中可以看出：GPS三频卫星IFCB高频分量的RMS统计量均在7.5～8.8 mm之间，不同卫星之间差别不大；而低频分量的RMS统计量并不一致。对于Block IIF卫星而言，低频分量的 RMS统计量从0.02到0.08 m，表明Block IIF卫星的IFCB存在明显的时变特性。而Block III卫星低频分量的RMS统计量均低于0.01 m，因此可以说明Block III卫星IFCB的时变特性并不显著。但结合上节Block III卫星IFCB的单日RMS统计量也较低，可以说明Block III卫星的IFCB时变特性相较于Block IIF卫星已经得到了明显的削弱，接下来仅对Block IIF卫星进行讨论。

3.3 IFCB预报及其对三频PPP的影响

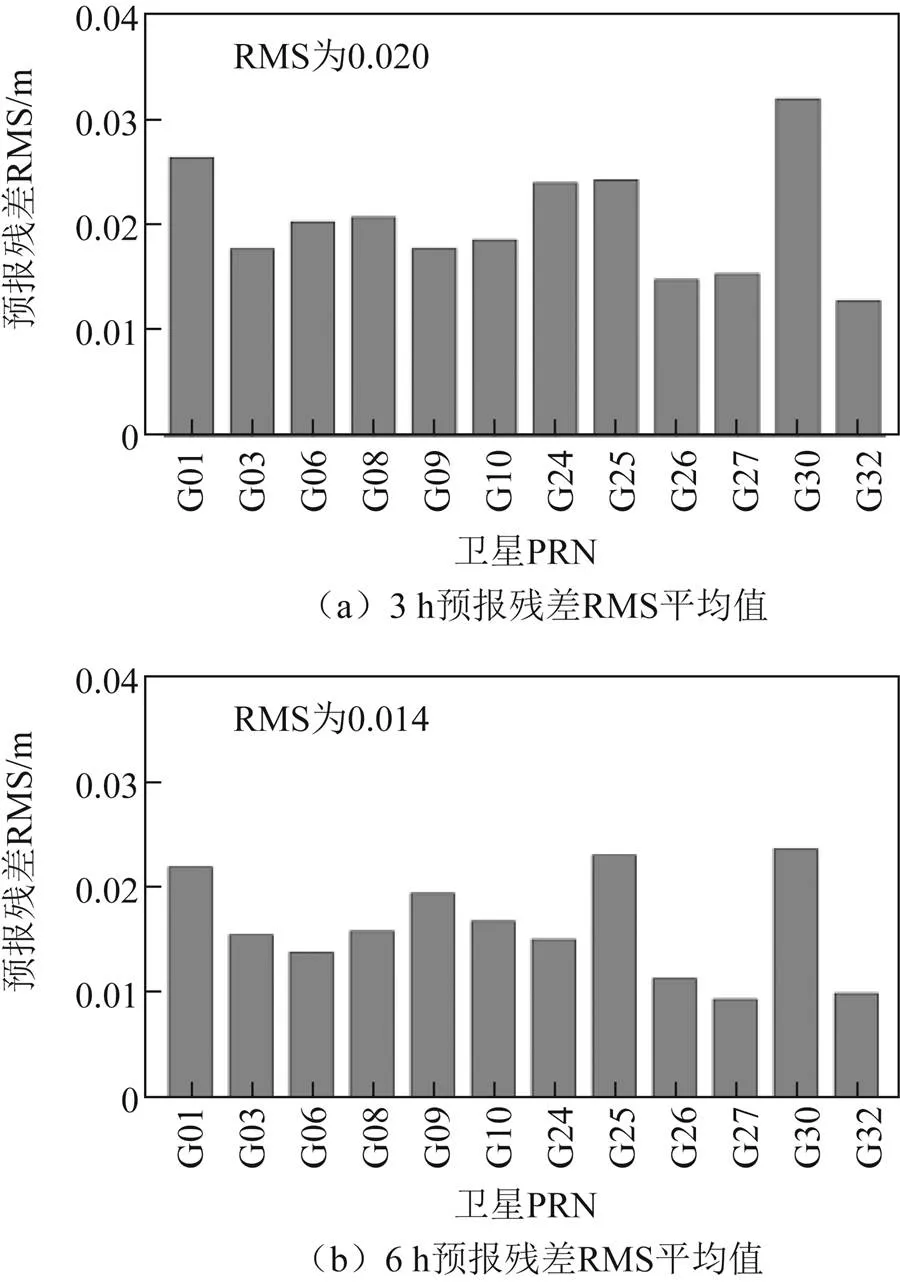
基于2021-05-01—2021-05-30的IFCB数据，利用式（8）对单日IFCB进行拟合，并向后滑动预报24 h，以当日估计的IFCB作为真值，利用RMS作为预报精度的统计量进行分析。图4给出了IFCB 预报残差的 RMS平均值。

从图中可以看出：单日预报精度随预报时长的增加而降低，预报时长为3、6、12、24 h，预报精度分别为0.014、0.016、0.017、0.020 m；对于单颗卫星而言，G26、G27预报效果最佳，24 h预报精度优于0.015 m。

互相关系数能有效反映IFCB预报值与当日估计值之间变化特征的一致性，其计算公式为

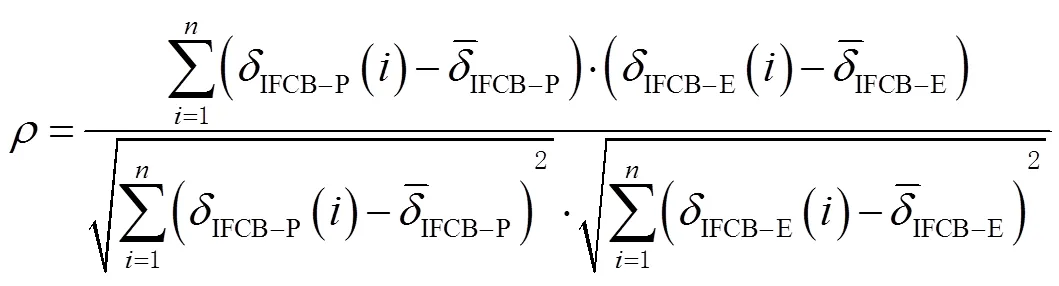
式中：n为总历元数；、分别为IFCB预报值与估计值；、分别为IFCB预报值与估计值的均值。图5给出了预报值与当日估计值之间的互相关系数统计结果。

由图可知：统计样本中互相关系数大于0.5、0.8、0.9的分别能占总数据个数的98.2%、92%、78.6%，说明预报值与估计值变化趋势一致性较好。

为了分析IFCB预报值对于三频PPP的影响，选取2021年5月2日观测条件较好的几个参考站分别进行静态PPP和动态PPP实验。实验方案共分为2种，第一种是利用IFCB预报值改正的三频PPP，第二种是不进行IFCB改正的三频PPP。通常认为单个方向定位误差在10 cm内并在之后一直处于此范围内即为该方向定位收敛，定位精度为定位收敛后的定位误差的RMS。

图6为LEIJ站静态PPP定位误差曲线。

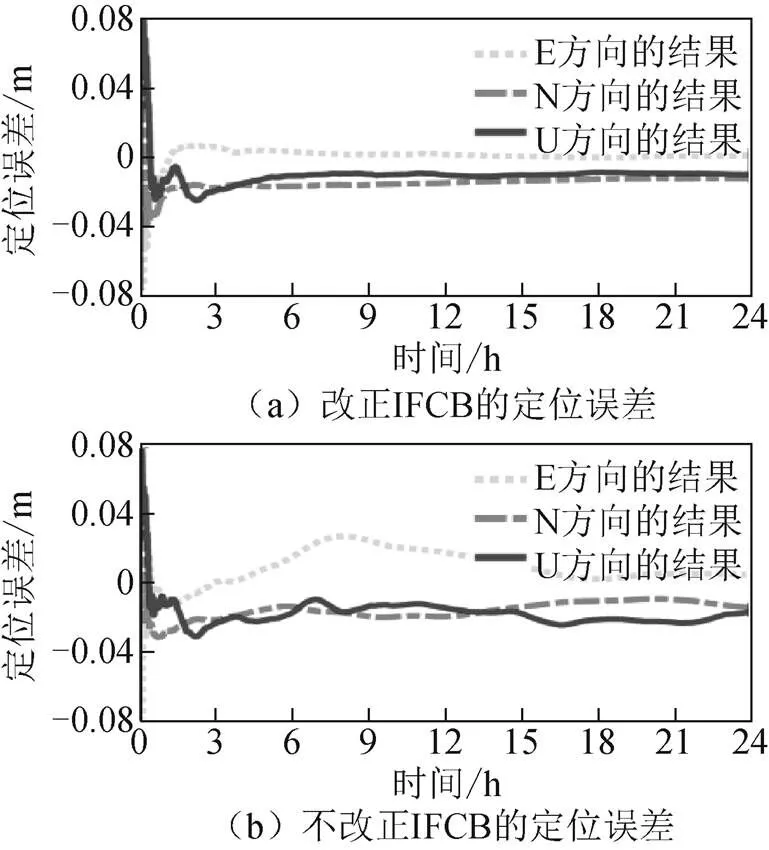
图6 LEIJ站静态PPP定位结果

从图中可以看出：不改正IFCB的定位曲线波动较大，在E、N、U 3个方向上定位精度分别为7.0、6.6、18.1 mm；而利用IFCB预报值改正后定位曲线则较为平稳，在E、N、U 3个方向上的定位精度分别为3.2、4.0、13.6 mm，与不改正IFCB相比分别提升了3.8、2.6、4.5 mm；另外，在收敛时间方面，不改正IFCB在E、N、U3个方向上收敛时间分别为21、17.5、24.5 min，利用IFCB预报值改正后分别为22、18.5、28.5 min，U方向提升最为显著。对于所有所选参考站而言，IFCB改正后定位精度在E、N、U 3个方向上分别提升了29.4%、39.4%、35%。

如图7所示为全部所选参考站静态PPP收敛时间统计结果，并给出了每个方向收敛时间的平均值。

从图中可以看出，利用IFCB改正后的三频PPP收敛时间明显减少，多个参考站在E、N、U 3个方向上收敛时间分别缩短了17.3%、21.6%、17.8%。总的来说，利用IFCB预报值改正能有效提升静态三频PPP的定位精度，同时缩短收敛时间。

同样以LEIJ站为例，图8展示了动态PPP定位误差曲线。

图8 LEIJ站动态PPP定位结果

从图中可以看出，利用IFCB预报值改正对动态PPP定位结果影响显著，与不改正IFCB相比，定位结果的稳定性有较大改善。不改正IFCB在E、N、U 3个方向的定位精度分别为3.7、2.6、6.8 cm，利用IFCB预报值改正后定位精度分别为1.7、2.0、2.0 cm，U方向提升最显著，提升了70.6%。对于全部所选参考站而言，利用IFCB预报值进行改正后，多个参考站E、N、U 3个方向定位精度分别从3.5、2.5、6.5 cm提高到了2.3、2.0、3.4 cm，分别提升了34.3%、20.0%、47.7%。

由于非模型化误差会呈现在观测值验后残差中，因此若不改正IFCB，即将IFCB作为常数估计，相位硬件延迟的时变部分会被相位验后残差吸收，使相位验后残差增加并呈现出系统误差。图9和图10给出了站L1、L2、L5载波相位验后残差的时间序列。

从图中可以看出，利用IFCB预报值进行改正后，显著消除了载波相位验后残差中的系统误差，同时L1、L2、L5频点的相位验后残差RMS分别从2.9、7.6、6.7 mm降低到了2.6、2.5、2.2 mm。

图9 LEIJ站改正IFCB的载波相位验后残差时间序列

4 结束语

本文基于GFIF组合的历元差分方法估计了全部在轨的GPS三频卫星的IFCB，对其变化特性进行分析。分析结果显示：Block IIF卫星IFCB单日内变化从厘米到分米不等，存在明显的时变特性；而BLOCK III卫星单日内变化量级较小，通常不超过1 cm，IFCB的时变特性相比于Block IIF卫星得到了明显的削弱。另外利用快速傅里叶变换对Block IIF卫星IFCB的周期性进行分析，发现Block IIF卫星的IFCB序列存在12、6、8、4、4.8 h以及3 h的周期变化，以此建立高阶谐波模型对IFCB进行预报，3、6、12、24 h预报精度分别为0.014、0.016、0.017、0.020 m。最后通过全球分布的多个参考站数据进行静态、动态三频PPP实验。对于静态PPP，利用IFCB预报值改正后，定位精度在E、N、U 3个方向上分别提升了29.4%、39.4%、35%；而对于动态PPP，利用IFCB预报值改正后，定位精度在E、N、U 3个方向上分别提升了34.3%、20.0%、47.7%，同时有效消除了载波相位验后残差中的系统误差。说明利用高阶谐波模型进行IFCB预报可以满足实时三频PPP的应用需要。

[1] 刘健,曹冲. 全球卫星导航系统发展现状与趋势[J]. 导航定位学报, 2020, 8(1):1-8.

[2] GENG J H, BOCK Y. Triple-frequency GPS precise point positioning with rapid ambiguity resolution[J]. Journal of Geodesy, 2013, 87(5): 449-460.

[3] TSAI Y H, YANG W C, CHANG F R, et al. Using multi-frequency for GPS positioning and receiver autonomous integrity monitoring[C]//Proceedings of the 2004 IEEE International Conference on Control Applications. IEEE, 2004, 1: 205-210.

[4] LIU W X, MOU W H, WANG F X. A new unequal-weighted triple-frequency first order ionosphere correction algorithm and its application in COMPASS[J]. Science China Physics, Mechanics and Astronomy, 2012, 55: 546-552.

[5] MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Three's the challenge: a close look at GPS SVN62 triple-frequency signal combinations finds carrier-phase variations on the new L5[J]. GPS World, 2010, 21(8): 8-19.

[6] MONTENBRUCK O, HUGENTOBLER U, DACH R, et al. Apparent clock variations of the Block IIF-1 (SVN62) GPS satellite[J]. GPS Solutions, 2012, 16(3): 303-313.

[7] LI H J, ZHOU X H, WU B, et al. Estimation of the inter-frequency clock bias for the satellites of PRN25 and PRN01[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(11): 2186-2193.

[8] LI H J, ZHOU X H, WU B. Fast estimation and analysis of the inter-frequency clock bias for Block IIF satellites[J]. GPS Solutions, 2013, 17(3): 347-355.

[9] GUO J, GENG J H. GPS satellite clock determination in case of inter-frequency clock biases for triple-frequency precise point positioning[J]. Journal of Geodesy, 2018, 92(10): 1133-1142.

[10] PAN L, ZHANG X H, LI X X, et al. GPS inter-frequency clock bias modeling and prediction for real-time precise point positioning[J]. GPS Solutions, 2018, 22(3): 1-15.

[11] QU L Z, DU M Y, WANG J, et al. Precise point positioning ambiguity resolution by integrating BDS-3e into BDS-2 and GPS[J]. GPS Solutions, 2019, 23(3): 1-11.

[12] PAN L, ZHANG X H, LI X X, et al. Characteristics of inter-frequency clock bias for Block IIF satellites and its effect on triple-frequency GPS precise point positioning[J]. GPS Solutions, 2017, 21(2): 811-822.

[13] DAUBECHIES I. Orthonormal bases of compactly supported wavelets[J]. Communications on Pure and Applied Mathematics, 1988, 41(7): 909-996.

Analysis of GPS inter-frequency clock bias characteristics and its effect on triple frequency PPP

ZHANG Pu, QU Lizhong, WANG Luping, WANG Haoyu

（Beijing University of Civil Engineering and Architecture, Beijing 102616, China）

Aiming at the problem that the inter-frequency clock bias (IFCB) of global positioning system (GPS) significantly affects the positioning performance of multi-frequency precise point positioning (PPP), the paper analyzed the variation characteristics of IFCB for all GPS triple-frequency satellites: it was known that the IFCB of Block IIF satellite varied from centimeters to decimeters in a single day with obvious time-varying characteristics, while the variation of Block III satellite in a single day was smaller, usually not more than 1 cm, and the time-varying characteristics of IFCB were significantly weakened compared with Block IIF satellite; at the same time, the IFCB of the Block IIF satellite had periodic changes of 12, 6, 8, 4, 4.8 and 3 h, based on which the IFCB high-order harmonic model was established. Experimental result showed that for static PPP, the positioning accuracy could be improved by 29.4%, 39.4% and 35% in the three directions of E, N and U, respectively, after applying the predicted IFCB correction; for kinematic PPP, after applying the predicted IFCB correction, the positioning accuracy could be improved by 34.3%, 20.0% and 47.7% in the three directions of E, N and U, respectively, and the systematic error in the phase residuals could be effectively eliminated.

global positioning system (GPS); inter-frequency clock bias (IFCB); feature analysis; modeling and predicting; precise point positioning (PPP)

P228

A

2095-4999(2023)02-0013-08

张蒲, 屈利忠, 王鲁平, 等. GPS频间钟差特性分析及其对三频PPP的影响[J]. 导航定位学报, 2023, 11(2): 13-20.（ZHANG Pu, QU Lizhong, WANG Luping, et al. Analysis of GPS inter-frequency clock bias characteristics and its effect on triple frequency PPP[J]. Journal of Navigation and Positioning, 2023, 11(2): 13-20.）DOI:10.16547/j.cnki.10-1096.20230202.

2022-05-04

国家青年自然科学基金项目（42104026）；北京市青年自然科学基金项目（4204094）；北京市教育委员会科技计划面上项目（KM201910016007）。

张蒲（1997—），男，北京人，硕士研究生，研究方向为多频多模精密定位技术。

屈利忠（1986—），男，河南郑州人，博士，副教授，研究方向为多频多模精密定位技术。