面向未知环境的空间机械臂自适应阻抗控制研究

戚毅凡, 贾英宏, 赵宝山, 洪闻青

1.昆明物理研究所, 昆明 650223 2.北京航空航天大学, 北京 102206 3.天津航天机电设备研究所, 天津市微低重力环境模拟技术重点实验室, 天津 300301

0 引 言

由于太空环境的复杂性以及科学技术的限制,许多空间任务尚不能通过航天员出舱进行,因此空间机械臂成为了执行空间任务中不可或缺的装备[1-2].在轨操作过程中,一般要求空间机械臂具有柔顺控制能力,而阻抗控制算法是最常用的柔顺控制算法,其基本原理是建立机械臂末端的接触力与多阶位置偏差之间的动态关系[3].目前机械臂的阻抗控制多数是根据二阶位置偏差的反馈实现,在需要对末端接触力、位置进行同时控制的场合应用较多[4-5].阻抗控制中,阻抗参数的选择决定了控制器的柔顺性能,传统阻抗控制器中阻抗参数通常为固定值,无法适应环境参数变化[6-7].若阻抗参数能随环境实时调整,则阻抗控制器的柔顺控制效果会优于阻抗参数固定的情况[8].

在机械臂柔顺控制的研究中,接触模型通常选择弹簧-阻尼模型[9-10].空间机械臂工作环境具有较高的不确定性,空间机械臂在实际操作中,精确的环境刚度和环境阻尼难以准确获取,而且环境刚度通常比较大,参考位置较小的偏差就会导致较大的力控制误差[11].不同的接触环境,其刚度、阻尼不同;即使在相同的接触环境下,机械臂末端接触力的改变也会导致环境的刚度、阻尼变化[12].针对环境信息变化下的空间机械臂柔顺控制问题,众多学者进行了研究.李强采用Eye-to-Hand的单目视觉私服结构,结合力传感器提出了一种力觉/视觉自适应控制方法以实现环境刚度不确定下的柔顺控制[13].HAMEDANI提出了一种自适应阻抗方法,通过跟踪机械臂末端所需要的接触力来调整阻抗参数以适应变化的环境[14].

为了使传统阻抗算法对不同环境或变化的环境具有更好的适应能力,提出了一种根据目标信息估计阻抗参数自调整的自适应阻抗控制方法.首先通过计算阻抗控制接触过程中接触力及位移的动态响应,并据此设计阻抗控制性能指标.其次利用最小二乘法在线估计环境参数,并在此基础上,由阻抗性能指标最小设计阻抗参数的自适应规律.基于平面2自由度机械臂的仿真结果表明,该阻抗参数自调整方法优化了阻抗控制器的控制性能,提高了阻抗控制器的鲁棒性及对环境的适应能力.

1 空间机械臂及任务建模

本文以如图1所示的平面2自由度机械臂系统作为研究对象,系统由卫星基座与两连杆机械臂构成.卫星基座可以在平面内进行自由的移动和转动,连杆1与2分别由2个单自由度的旋转关节连接,系统为5自由度系统.

图1 平面2自由度空间机械臂系统示意图

在惯性坐标系下,x0和y0为卫星基座的质心位置,θ0为卫星基座的转角(姿态);θ1和θ2为机械臂2个关节的转角.针对平台本体无控情况,机械臂系统的动力学方程可以写为[15]

(1)

式中:Fc=[FxbFybTzbτ1τ2]T,Fxb、Fyb、Tzb为卫星基座控制力及力矩;τ1、τ2为机械臂关节控制力矩;θ=[x0y0θ0θ1θ2]T;D为质量阵,为对称阵;H为离心力和哥氏力矢量;Fe为机械臂末端与目标的接触力;J为雅克比矩阵.机械臂正运动学即由各关节转角计算获得机械臂末端位置,其可通过几何关系推导得到.将正运动学方程求导便可获得机械臂末端速度的计算式[16]

(2)

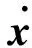
2 自适应阻抗算法

2.1 阻抗控制及动态响应指标求解

1985年,HOGAN[17]提出了阻抗控制算法,该算法建立了力、位置、速度的阻抗关系式,仅需要一个控制策略即可同时控制力和位置.阻抗关系式通常使用二阶形式[18]

(3)

其中:Fd为机械臂末端期望接触力;M为惯性系数矩阵,B为阻尼系数矩阵,K为刚度系数矩阵,均为对称阵;xd为机械臂末端的期望位置,x为机械臂末端位置.利用空间机械臂逆动力学及计算控制力矩法设计控制律,控制力矩τm可设计为

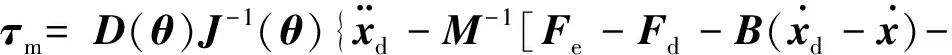
(4)

机械臂末端与环境的接触模型设定为Kelvin-Voigt模型[19],即弹簧阻尼模型.假设机械臂为纯刚体,在惯性坐标系下接触力仅是与机械臂末端位置和速度有关的函数,即

(5)

若环境即接触对象为一自由漂浮物体,则xe为惯性坐标系下的目标位置;Be为环境阻尼矩阵,Ke为环境刚度矩阵,均为对角阵.将式(4)和式(5)代入式(3),可以得到机械臂末端的稳态位置xss、稳态接触力Fss和稳态力误差Efss分别为

(6)

至此,推导了阻抗接触过程中机械臂末端接触力及位置的动态响应,为后文设计阻抗参数调整规则奠定了基础.

2.2 最小二乘法的参数辨识

弹簧-阻尼接触模型在正交方向上可以解耦,根据机械臂末端接触力和位置的反馈,采用最小二乘法对本体坐标系xbybob下x方向的环境刚度和环境阻尼进行估计,估计结果为

(7)

2.3 阻抗参数自整定的自适应阻抗控制

由式(5)～(6)可知,阻抗控制下的空间机械臂如果不能精确地获得环境信息,则会导致稳态力误差和稳态位置误差的产生.

将控制力矩代入空间机械臂动力学方程,即将式(4)代入式(1)

(8)

其中,位置误差eP=x-xd,力误差eF=Fe-Fd.将式(5)代入eF=Fe-Fd可得

(9)

将式(9)代入式(8)可得

(10)

空间机械臂与环境的接触力在正交方向可以解耦,为了简化问题,只在本体坐标系xbybob下x方向上进行研究,其余正交方向推导类似.以力控制和位置控制误差最小为目标,定义本体坐标系xbybob下x方向的阻抗控制性能指标Jim为

Jim=α(xss-xd)2+β(Fss-Fd)2

(11)

其中:α、β为权重系数,表示在阻抗控制中力控制和位置控制的权重要求,单位分别为m-2和N-2;阻抗控制性能指标Jim的大小表示柔顺控制效果的优劣,数值越小则柔顺控制效果越优.将式(6)代入式(11)可得

(12)

由式(12)可以看出,阻抗性能指标是关于环境刚度的函数,所以利用该函数来设计阻抗刚度参数的自适应律,即当阻抗性能指标最小时刚度系数为最优值K*

(13)

求解式(13)获得阻抗刚度系数的自适应律式为

(14)

在柔顺控制中,超调量即最大接触力同样是衡量柔顺性能优劣的重要指标.阻抗控制下的机械臂与目标闭环系统为二阶系统,由二阶系统的动态响应特性可知,系统处于过阻尼状态时的性能较优,且在一定范围内阻尼比越大,超调量越小[20].假定系统的阻尼比为ξ,则

(15)

假定阻尼比ξ为一个可调节的参数,则阻抗阻尼系数自适应律为

(16)

至此,已经获得阻抗阻尼和刚度参数的自适应方法.阻抗惯性系数M为用户设定值,为研究不同惯性系数对自适应阻抗控制的影响,选取惯性系数M分别等于1、2、3、4、5进行仿真,仿真对象为平面2自由度机械臂系统,机械臂末端接触空间中一自由漂浮物体,假定卫星基座受控,其位姿保持不变.设定目标刚度Ke=20 000 N/m、目标阻尼Be=500(N·s)/m,结果如图2所示.

图2 不同惯性系数下机械臂末端接触力

由结果可以看出,在自适应阻抗控制中惯性系数越小,调节时间越快,最大接触力越小,柔顺性能越好.所以选择一个较小的惯性系数M=1,作为后文仿真的初始条件.

3 数值仿真

平面2自由度机械臂系统由卫星基座与两根连杆构成,两根连杆的质量分别为m1、m2,长度分别为l1、l2.在后文仿真中,设置两根连杆的质量m1=m2=0.672 3 kg,两根连杆的长度l1=l2=0.2,卫星基座和连杆1、连杆1和连杆2分别由2个单自由度的旋转关节连接,系统为2自由度系统.空间机械臂接触过程时间通常为秒级,故仿真步长设置为0.01 s.空间机械臂在进行接触操作时基座属于受控状态,接触过程对基座控制的影响较小,基座始终可以保持期望位置姿态.由于基座控制不是本文的重点,故在仿真中假设基座固定.

3.1 不同阻尼比的自适应阻抗控制

系统的阻尼比为预设参数,其选择对自适应阻抗控制的柔顺控制效果产生重要影响.为了研究阻尼比对控制效果的影响,设定初始阻抗参数为M=1、B=50、K=200,目标刚度Ke=20 000 N/m、目标阻尼Be=500 N·s/m,期望接触力Fd=10 N.在之后仿真中均假定卫星基座受控,其位姿保持不变.阻尼比分别取1、6、11、16、21进行数值仿真.其仿真结果的动态响应如表1所示.

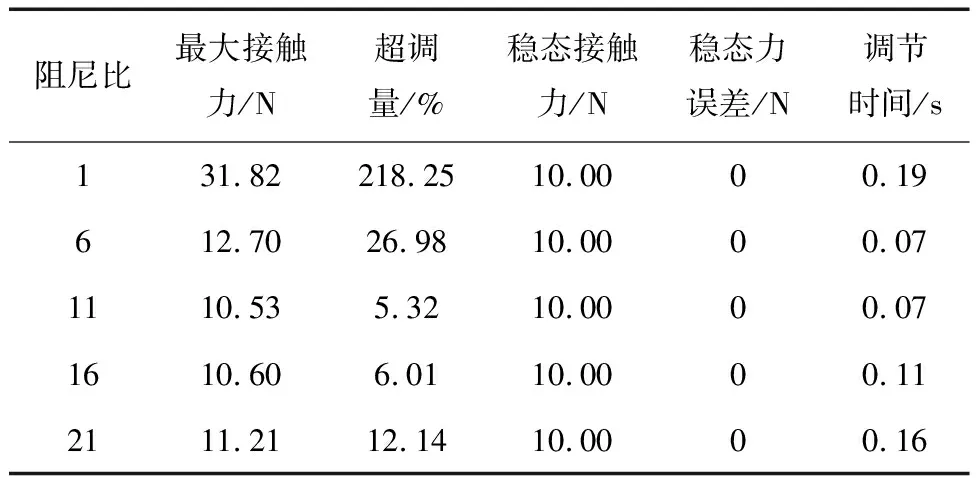
表1 不同阻尼比下机械臂末端接触力的动态响应

由表1可知,随着阻尼比的增大,最大接触力先减小后增加,调节时间先缩短后增长.由此可见对于同一组控制器参数,阻尼比存在一个最优值.无论阻尼比如何变化,自适应阻抗控制器控制的机械臂都没有稳态力误差,能实现精准的力控制.通过对比仿真结果,选取柔顺控制效果较好的阻尼比ξ=11作为后文仿真中的控制器参数.

3.2 自适应阻抗控制对不同目标刚度的适应性

机械臂末端在接触过程中速度非常小,且目标刚度远远大于目标阻尼,故在验证自适应阻抗控制器对不同环境的适应能力时,只设计不同的目标刚度进行仿真,目标阻尼保持不变.分别设置目标刚度为5 000 N/m、10 000 N/m、15 000 N/m、20 000 N/m、25 000 N/m,目标阻尼保持500 N·s/m不变,与传统阻抗控制器进行比较,其动态响应对比如表2所示.传统阻抗控制器质量系数为1,阻尼系数为10,刚度系数为80.

表2 传统阻抗控制器与自适应阻抗控制器的接触力动态响应对比

由表2可知,对于传统阻抗控制器,若阻抗参数不变,随着目标刚度增加最大接触力增大,稳态力误差增大,调节时间变长.对于自适应阻抗控制器,随着目标刚度增加,最大接触力无明显变化且超调量始终较小.自适应阻抗控制下的机械臂稳态力误差始终为零,且调节时间随着目标刚度增加而减小.所以自适应阻抗控制器相较于传统阻抗控制器对不同的接触环境具有更强的适应能力,柔顺控制效果更佳,力控制精确更高.

3.3 自适应阻抗控制对目标刚度变化的适应性

根据文献[12],机械臂末端在与目标发生接触时目标刚度会发生变化.若目标为不均匀介质,则目标刚度也可能发生突变.本节针对环境刚度发生连续改变和突变两种情况进行研究,并验证自适应阻抗控制在该情况下的控制效果.设置初始环境刚度为2 000 N/m,在仿真开始第1 s后突变为8 000 N/m,第2 s后突变为4 000 N/m,环境阻尼保持500(N·s)/m不变,验证自适应阻抗控制器在目标刚度突变情况下的柔顺控制效果.目标刚度的估计值如图3所示,机械臂末端接触力如图4所示.

图3 目标刚度突变时目标信息估计

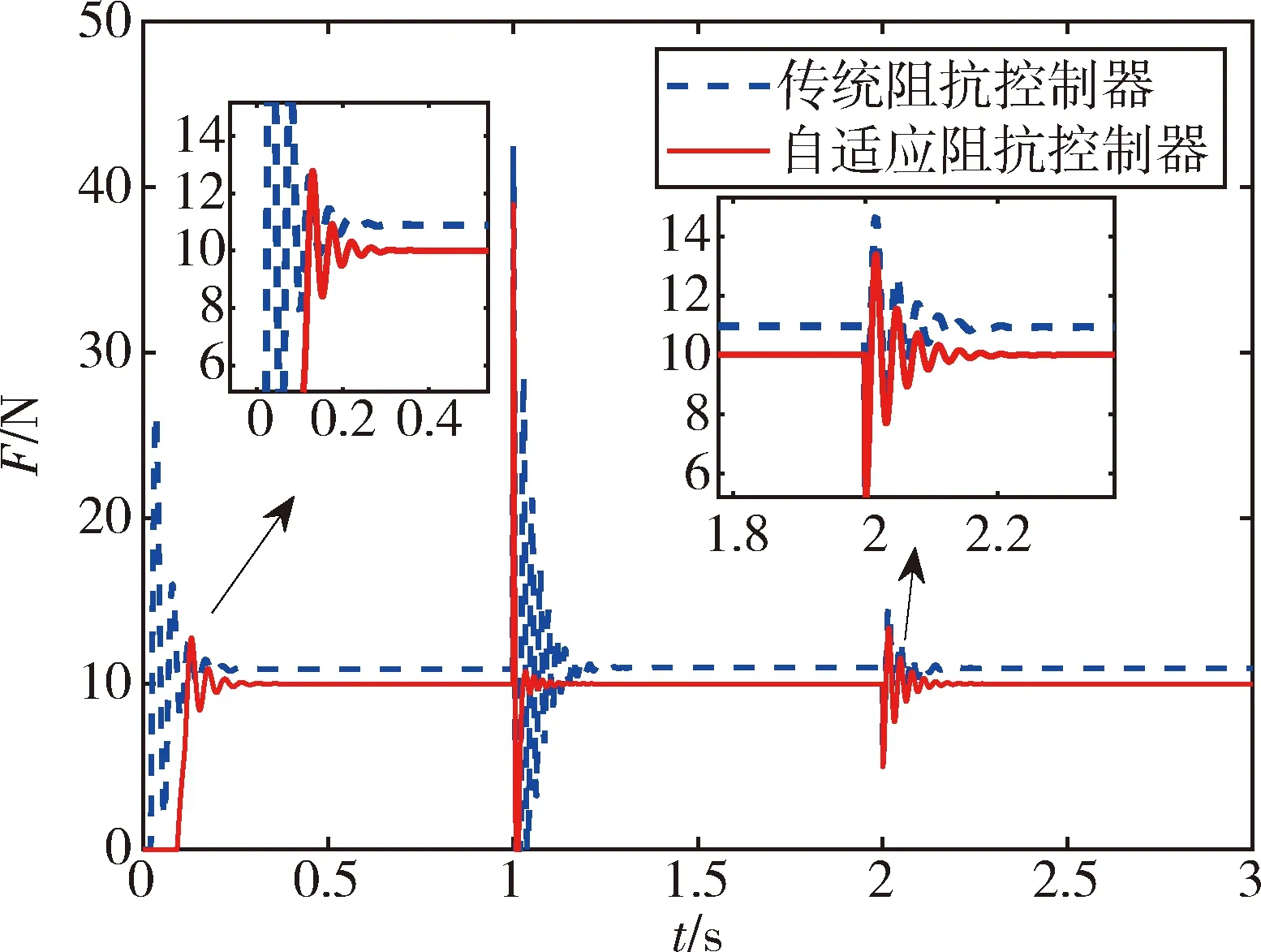
图4 目标刚度突变时机械臂末端接触力

由图4可以发现,在环境刚度发生突变时,自适应阻抗控制器相比传统阻抗控制器能更快速地适应环境刚度的改变,使接触力更快地到达稳定值,且稳态接触力与期望接触力相同,接触力稳态误差始终为零.

研究环境刚度发生渐变问题时,设置初始环境刚度为2 000 N/m,在仿真开始第3 s后渐变为8 000 N/m,环境刚度变化为线性变化,变化率为2 000 N/(m·s).环境阻尼保持500(N·s)/m不变,验证自适应阻抗控制器在环境度突变情况下的柔顺控制效果.目标刚度的估计值如图5所示,机械臂末端接触力如图6所示.

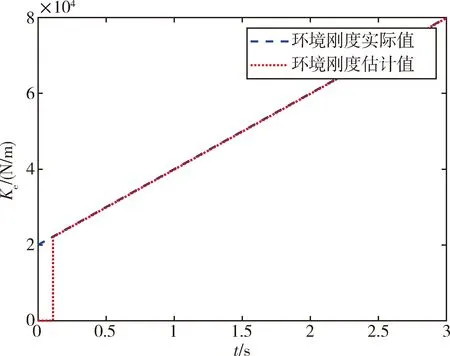
图5 目标刚度渐变时目标信息估计

由图6可以发现,无论是传统阻抗控制器还是自适应阻抗控制器,对环境刚度较小的渐变都能有适应作用.但传统阻抗控制器的稳态力误差依然存在,而自适应阻抗控制器无稳态力误差.

图6 目标刚度渐变时机械臂末端接触力

4 结 论

基于对阻抗控制接触过程研究,提出了一种自适应阻抗控制方法.根据阻抗控制接触过程中的动态响应设计阻抗控制性能指标;由性能指标最小设计了阻抗阻尼系数和刚度系数的调整律,并通过仿真设定较优的惯性系数;通过仿真分析不同阻尼比对自适应阻抗控制效果的影响,验证了自适应阻抗控制器对接触环境变化的适应能力.与传统阻抗控制器相比,阻抗参数自调整的自适应阻抗控制器在力控制精确性、减小最大接触力和适应不同接触环境上有明显的优势.