基于卫星数字并行系统的星座成像调度方法

余 快, 张 鹏, 陈 斌, 葛 萌

1.中国空间技术研究院遥感卫星总体部, 北京 100094 2.北京控制工程研究所, 北京 100094 3.中国空间技术研究院杭州中心, 杭州 310024

0 引 言

随着航天技术飞速发展,以多星组网的方式协同完成空间任务,是卫星技术发展的重要方向之一.在遥感领域,通过遥感卫星星座对地面目标进行观测能够大大提高成像范围和观测效率,其中多星任务规划是关键技术之一.遥感卫星星座成像调度是指通过调度和分配可用的卫星观测资源,对多个地面目标点进行成像.这类问题是一类典型的含有多种复杂约束的多星任务规划问题.一般来说,相对于多个待观测的目标而言,可用的遥感卫星资源总是短缺的,因此,需要通过优化成像调度方案解决星座资源合理分配问题.

早在2000年,为了解决大规模商业卫星的任务规划问题,PEMBERTON等提出使用一种商业化卫星任务规划系统(generic resource, event, and activity scheduler,GREAS)[1-2],解决单颗卫星在满足相机侧摆能力及星上能源等约束时的成像任务调度问题.随着在轨卫星数量逐渐增加,卫星用户或运营商关注的空间资源已不再是相互独立的单星资源,星座的整体应用以及多星任务的协同调度成为如何优化利用宝贵空间资源的关键.面向复杂的多星组网业务,必须通过计算机技术解决星座资源的调度及任务规划问题[3-7].特别是在卫星种类、性能不尽相同,任务时空分布不均的复杂情形中,传统的依靠手工计算或单星任务规划的模式已无法满足发展的需求.近年来,国内外很多学者开展了卫星成像调度方法的研究工作,这些工作主要分为静态方法和动态方法2类.静态方法是以卫星资源、载荷能力、时间窗口等作为约束[8-12],将成像调度问题描述为经典优化问题.针对这类问题,学者们设计了多种算法对其进行求解[13-15].这些静态方法尽管从一定程度上解决了单星或多星的任务调度问题,但无论是约束条件的设置,还是优化指标的构造都是确定性的,因此,难以适应任务调度中的动态因素及不确定性.针对卫星成像调度中的动态因素,学者们也提出了很多解决方法[16].刘洋等[17]考虑了规划方案中动态增加新任务的情形,定义了最小化扰动测度指标,建立了多星动态调度优化问题,通过启发式算法对优化问题进行求解.WANG等在卫星成像任务规划中考虑了时间窗口拥堵和任务重叠2种情形,并针对不同规模的动态任务规划问题提出2种启发式算法进行问题求解[18].刘晔伟等提出了一种基于贪婪算法与合同网结合的分布式卫星系统(distributed satellites system,DSS)动态任务规划算法,解决天基网络通信能力受限下的动态任务规划问题[19].杨超等[20]提出了一种结合蚁群算法和模拟退火算法的多星多任务分配算法,解决了蚁群算法易陷入早熟以及模拟退火算法前期搜索速度慢的问题.上述方法大多将任务调度与卫星动态解耦,在任务调度问题的建模与求解过程中,卫星的控制过程往往通过确定的参数或简化后的代数方程来刻画,这种描述形式时效性不高,很难反映空间环境中实时出现的不确定因素以及卫星运行参数变化对任务调度方案的影响,因此,为了使求解的调度方案更具可行性和时效性,需要在问题描述和求解中关联更真实的卫星动态模型.

为了真实模拟卫星星座运行及控制过程,本文提出一种卫星数字并行系统.首先,在系统中建立数字孪生卫星,模拟卫星GNC分系统、数管分系统、测控分系统功能,接收并执行卫星控制指令,并以遥测数据的形式反映卫星姿态和轨道控制过程.其次,考虑卫星多目标成像中的能量、时间窗口、光照及气象条件约束,以目标点重访时间为优化指标,构建星座成像调度优化问题.再次,通过卫星数字并行系统的加速仿真得到多目标成像序列的可行解集,并通过求解优化问题得到多目标点重访频率最高的星座成像调度方案.最后,通过仿真说明本文提出方法的有效性.

1 卫星数字并行系统

与真实卫星功能及行为存在一致映射关系的虚拟卫星模型称为数字孪生卫星,采用数字孪生卫星可以对真实卫星在空间环境中的行为和性能进行仿真和模拟.数字孪生卫星与在轨运行卫星实体及相关的数据、模型及仿真服务共同构成卫星数字并行系统,如图1所示.

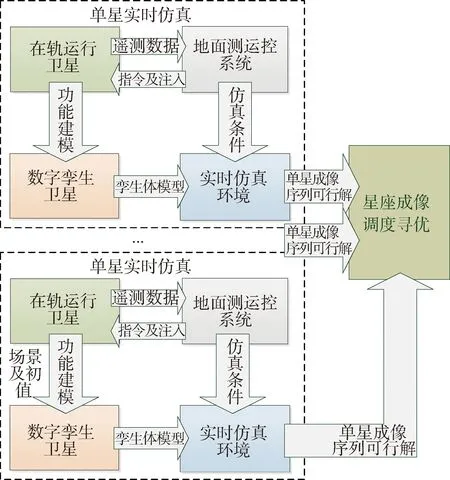
图1 卫星数字并行系统架构

卫星数字并行系统能够解决不同场景应用需求,不同的应用场景对数字孪生卫星的模型、数据及服务的需求有所不同,本文以星座成像调度为例,提出基于卫星数字并行系统的星座成像调度方法.详细实现流程如下:

1)分析星座成像调度任务需求,明确任务输入输出及设计约束.

2)构建星座中每颗卫星对应的数字孪生卫星模型,通过任务需求分析可知,在成像调度任务中需要对卫星的GNC分系统、数管分系统、测控分系统进行功能仿真,如图2所示.

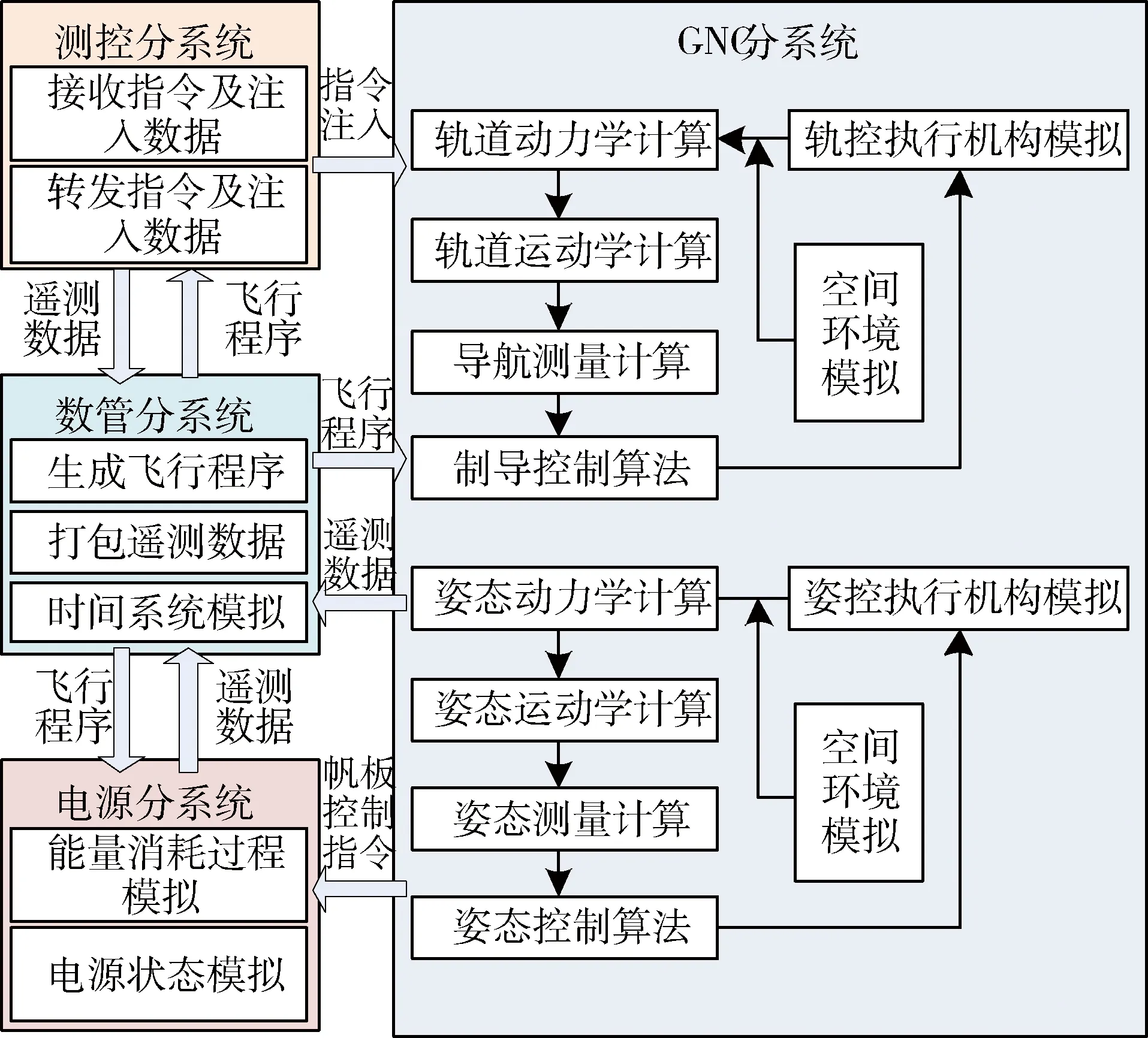
图2 数字孪生卫星组成

GNC分系统模型功能包括:模拟任务阶段的所有控制逻辑,以及系统模式切换过程;接收测控分系统或数管分系统转发的与GNC有关的遥控指令或注入数据,并模拟执行效果;模拟遥测参数变化过程,包括GNC各敏感器可用状态、视场及输出信息随空间环境变化等;模拟太阳翼控制时相关角度和状态变化;模拟各执行机构的控制过程及执行机构对卫星姿态和轨道的影响;模拟各飞行阶段轨道动力学、姿态动力学以及与姿态测量有关的外部环境.

数管分系统模型功能包括:模拟飞行程序,按照时间或状态条件模拟程控指令的发送或执行,将数管分系统以外的程控指令发送给对应的分系统;模拟数管分系统执行程控指令的效果;接收飞行程序的注入数据,并根据注入数据内容修改或更换飞行程序内容.

测控分系统模型功能包括:接收遥控指令或注入数据,检查遥控指令和注入数据的正确性;模拟测控分系统接收遥控指令或注入数据的执行效果;转发其它分系统的指令和注入数据;对接收到的上行数据进行实时存储,并能够进行实时或事后查询;接收数管分系统发出的程控指令,模拟相应的执行效果.

电源分系统模型功能是按照与任务状态一致的时序,模拟母线电压、充放电电流、电池电量、消耗功率等状态量变化过程.

3)建立在轨运行卫星与数字孪生卫星之间的数据通讯机制.当卫星处于测控弧段内时,通过实时遥测数据修正数字孪生卫星模型;当卫星处于测控弧段外时,通过数字孪生卫星对在轨卫星的运行状态进行预测.

4)建立系统仿真输入参数,设定约束条件,生成单星多目标成像序列构成样本变量空间,以循环扫描函数扫描样本空间内多目标成像序列,通过加速仿真对样本变量加速筛选出可行性多目标成像序列集.

定义星座成像调度优化指标函数,通过单星成像序列可行解的组合形成星座成像调度解空间,在空间内进行最优解搜索,得到使得指标函数最优的星座成像调度策略.

2 多目标成像问题描述

根据卫星多目标成像工作过程的分析,本文考虑卫星能量、时间窗口、光照及气象条件3类约束条件.卫星对多目标成像过程所消耗的能量需小于特定的阈值,整个成像过程需要在卫星通过目标区域的时间窗口内完成,同时,根据实时环境条件,卫星对地成像的目标点上空的气象条件应满足卫星的成像需求.

假设卫星在任务区域内有n个待成像的目标点,定义依次卫星进入任务区域的起始点为p0,离开任务区域的终止点为pf,在任务区域内依次对序号为p1、p2、…、pv的v个待成像的目标点成像,则p0→p1→p2→…→pv→pf为卫星在任务区域内的一条成像序列S.定义cij表示目标点i到目标点j关联关系,如果卫星连续顺序对目标点i到目标点j成像,则cij=1,否则cij=0.为便于描述,定义卫星依次对目标点i、目标点j成像的成像过程为“转出”目标点i,“转入”目标点j.

在一个成像序列中,本文约定卫星不对同一个目标点进行一次以上成像,因此有

(1)

一条完整地成像序列中,起始点p0只有一次转出过程,终止点pf只有一次转入过程,非起始点和终止点的目标点转入次数和转出次数相等,因此,有如下约束:

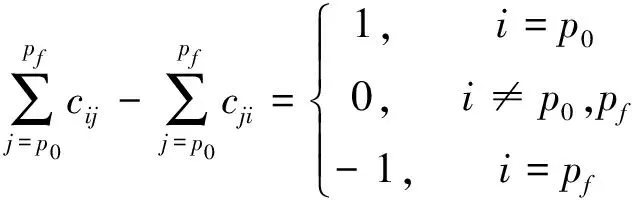
(2)

构造如式(3)所示的能量约束条件,表示卫星成像序列的可行解中目标点间转移的能量消耗之和需小于星上可用能量阈值.

(3)

式中,E表示星上可用能量阈值,eij表示从目标点i到目标点j卫星的能量消耗的影响因子.

构造如式(4)所示的时间窗口约束条件,表示卫星成像序列的可行解中目标点间转移的时间之和小于卫星经过任务区域的时间窗口.

(4)

式中,T表示卫星经过任务区域的时间窗口,τij表示从目标点i到目标点j卫星的时间消耗的影响因子.

构造如式(5)所示的光照及气象条件的约束,表示卫星成像序列的可行解中多目标成像质量影响因子之和应小于一定任务区域成像条件阈值.

(5)

式中,W表示任务区域成像条件阈值,wij表示从目标点i到目标点j光照及气象条件对成像质量的影响因子,wij的值越大,表示成像条件越差,wij的值越小,表示成像条件越好.

卫星数字并行系统,包含了卫星GNC分系统模型,能够对卫星在轨运行过程中的姿态、轨道变化及太阳翼矢量方向进行模拟,基于这些信息,电源分系统模型能够准确模拟星载电源充放电过程,进而判断卫星在多目标成像过程中能量消耗是否满足式(3)所示约束.GNC分系统模型能够真实模拟卫星侧摆成像的动态过程,因此,能够更真实地评估多目标成像所消耗的时间是否满足式(4)所示约束.此外,数字孪生卫星模型中还对空间环境进行了定量描述,可以以此为依据确定多目标成像过程中光照及气象条件是否满足式(5)所示的约束.综上,可以将卫星多目标成像序列作为输入条件,通过卫星数字并行系统对多目标成像过程进行加速仿真,验证多目标点构成的任意成像序列是否满足能量约束、时间窗口约束以及光照及气象条件的约束,进而得到可行解集Ω.如果成像序列S∈Ω,则S:p0→p1→p2→…→pv→pf满足上述约束.

3 星座成像调度

假设任务区域内有n个目标点待成像,星座中共有m颗卫星同时在任务区域内执行成像任务.这是一类典型的目标分配问题,解决这类问题的方式通常分为分布式和集中式2种,分布式方法是通过星间通信实现星间信息交互,并由单星依据自身及邻星状态进行自主任务规划,确定成像目标.分布式方法受限于星间链路传输能力及星上计算能力,对于全局信息感知及冲突消解等问题处理能力有限.为了解决这些问题,本文采用集中式方法,由地面卫星数字并行系统统一为星座进行任务规划,即所有执行成像任务的卫星均与地面站进行信息交互,系统根据每颗卫星的轨道、能源、幅宽、侧摆能力及成像窗口等信息为其指定成像目标.集中式方法不仅能在不依赖星间通信的情况下实现多星协同,而且由于系统部署于地面,可以不受算力限制,根据星座及目标全局信息生成的成像调度方案具有“更优的”任务效能.

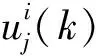
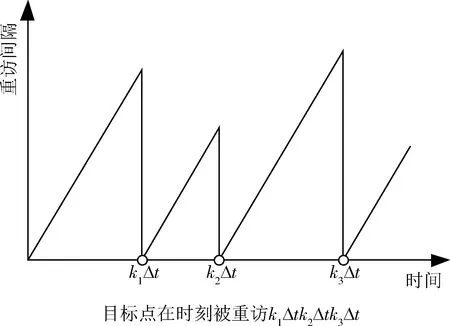
图3 重访间隔与目标被重访时刻

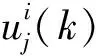
(6)

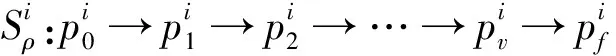
根据上述描述可知,目标点j的重访间隔随时间变化的规律为

(7)

引入状态变量X(k)和控制变量U(k)如下所示:

X(k)=[x1(k),x2(k),…,xn(k)]T

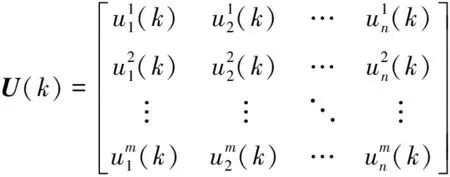
则所有目标点的重访间隔随时间更新规律可表示为

X(k+1)=F(X(k),U(k))

(8)

其中,

F(X(k),U(k))=

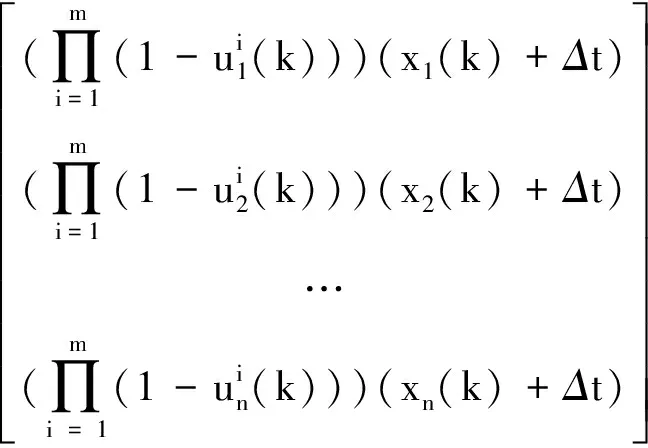
卫星数字并行系统能够记录所有目标点重访间隔的信息,即X(k),并根据式(8)所示递推关系,计算目标点在任意成像序列下的重访间隔变化规律.

为了使所有目标点的重访间隔在一定时间范围[k0Δt,kfΔt]内尽可能小,构造星座成像调度问题的指标函数为

(9)

其中,L(k)=diag{l1(k),l2(k),…,ln(k)},0≤lj(k)≤1表示在[k0Δt,kfΔt]内n个目标点的权重.目标点权重值在任务时间窗口内可以动态调整.

星座成像调度优化问题可描述为

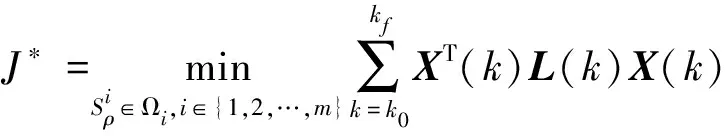
s.t.X(k+1)=F(X(k),U(k))

(10)

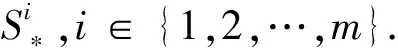
式(10)是一类广泛存在于实际工程中的约束优化问题,解决该问题的方法大体分为2类:确定性方法和随机性方法.确定性方法通常是基于梯度的搜索方法,如投影梯度法、简约梯度法、惩罚函数等.随机性方法包括遗传算法、模拟退火、禁忌搜索等.确定性方法可解释性强,但随着可行解空间增大,计算量会快速上升.随机性方法具有鲁棒性强、搜索效率高的特点,但有时会得到非全局最优解.本文重点在于将星座成像问题描述为式(10)所示的约束优化问题,但未对采用的寻优方法加以限定.相关研究人员可根据实际应用中可行解空间大小及计算资源,自行选取合适算法进行寻优计算.

4 仿真分析

为了对本文提出的星座成像调度方法的有效性和结果进行分析,本文在所构建的卫星数字并行系统进行了仿真实验.假设由同一轨道面内的3颗卫星在任务区域对16个目标点进行成像.

根据目标地理位置分布将目标点划分为4组,分别为

第1组:{目标点1、目标点2、目标点3、目标点4};

第2组:{目标点5、目标点6、目标点7、目标点8};

第3组:{目标点9、目标点10、目标点11、目标点12};

第4组:{目标点13、目标点14、目标点15、目标点16};

第1组至第4组目标点位置距离任务区域起始点由近及远,假设3颗卫星相隔2min进入任务区域,每颗卫星在运行经过目标区域时,顺序对每组目标点其中之一进行成像.因此每颗卫星成像序列中至多包含4个目标点.本例中考虑所有目标点权重均相同.

通过卫星数字并行系统求得3颗卫星满足能量约束、时间窗口约束、光照及气象条件约束的可行解集分别为Ω1、Ω2、Ω3.其中Ω1包含卫星50个成像序列可行解,Ω2包含卫星60个成像序列可行解,Ω3包含卫星45个成像序列可行解.

本文采用投影梯度法求解优化问题(10),得到3颗卫星最优成像序列分别为

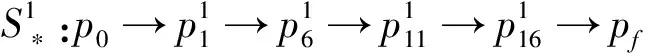
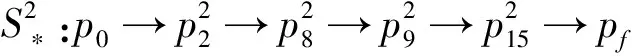
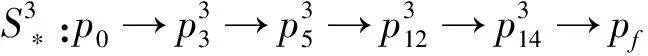
图4表示了3颗卫星最优成像序列随时间变化的规律.

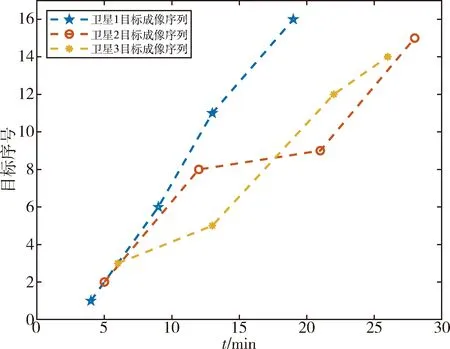
图4 3颗卫星最优成像序列

根据式(8)可得,3颗卫星经成像调度后,16个目标点的重访间隔随时间变化的规律如图5所示,其中由于目标4、目标7、目标10、目标13重访间隔初始值较小,所以未在统计周期内被访问,其它目标点都在卫星的访问时刻,重访间隔被清零.

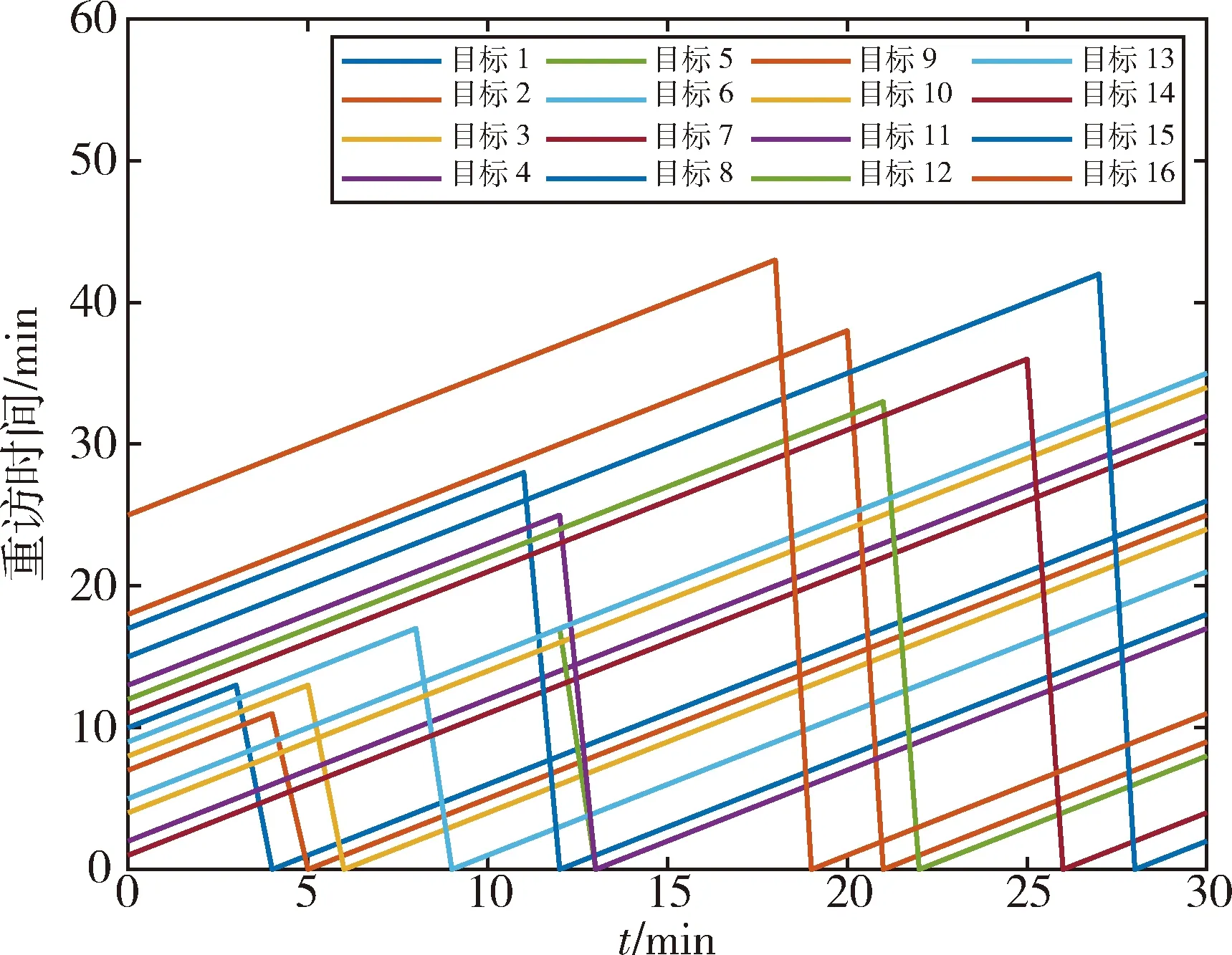
图5 目标点重访间隔随时间变化的规律

由图5可知,本文提出的星座成像调度可以保证多个目标点在卫星成像资源有限的情况下,重访时间间隔不会过长,为多目标成像任务提供了一种有效的成像调度解决方案,通过优化调度卫星资源提高了任务区域的成像效率.

5 结 论

本文针对遥感卫星星座成像调度问题开展了研究,提出一种卫星数字并行系统,模拟在轨卫星星座运行及控制过程.在系统中建立了模拟GNC分系统、数管分系统、测控分系统功能的数字孪生卫星,能够接收并执行真实卫星控制指令,并以遥测数据的形式反映卫星姿态和轨道控制过程.考虑卫星多目标成像中的能量、时间窗口、光照及气象条件约束,以目标点重访时间为优化指标,将星座成像调度问题建模为一类带有约束的优化问题.通过卫星数字并行系统的加速仿真得到了多目标成像序列的可行解集,并通过求解优化问题,得到多目标点重访频率最高的星座成像调度方案.